目录

🚀 摘要

🧱 第一部分：问题本质 —— 你的算子在和谁战斗？

⚙️ 第二部分：破墙实战 —— 从内存和计算两头夹击

战法一：对抗内存墙 —— 让数据“住”在计算单元旁边

战法二：粉碎计算墙 —— 让硬件干最擅长的活

🔨 第三部分：实战手记 —— 优化一个真实算子（以类LayerNorm为例）

优化前：一个“朴素”但低效的实现

优化后：一个高度流水化和向量化的版本

🧰 第四部分：优化工具箱与排错指南

系统性优化决策流程

常见“坑点”与解决方案

性能优化技巧清单（速查表）

🏆 第五部分：超越单个算子 —— 系统级视野

案例：从算子优化到模型级部署

前瞻性思考：未来还需要这样“手搓”吗？

📚 资源与结语

参考链接

写在最后

🚀 官方介绍

🚀 摘要

本文是一份来自一线实战的昇腾CANN算子优化全攻略。我将以多年老兵的视角，直击AI计算两大核心矛盾——内存墙与计算墙，用大白话拆解在Ascend C层面系统化攻克它们的完整方法论。文章将彻底避开空洞理论，聚焦于我们团队在优化MoE、Transformer等大模型关键算子时，那些真正起作用的技术细节、踩过的深坑和提炼出的通用心法。从性能分析定位、数据类型革命、访存优化黑科技到计算流水线重构，我将提供可复现的代码框架和决策流程，帮助你将算子性能提升一个数量级。

🧱 第一部分：问题本质 —— 你的算子在和谁战斗？

干了这么多年高性能计算，我越来越觉得，优化算子就像老中医看病，核心是准确辨证。你感觉算子“慢”，但到底是哪种“慢”？不搞清楚这个，所有优化都是瞎忙活。

现代AI芯片，尤其是像昇腾这样的NPU，理论算力（FLOPS）已经高到吓人。但为什么我们写的算子经常连理论值的30%都跑不到？因为有两个无形的“墙”挡在前面：

  1. 内存墙（Memory Wall）：计算单元吃得快，但数据喂得慢。数据从HBM（高带宽内存）搬到AI Core的片上缓存（UB），这个搬运过程的速度（带宽）和延迟，严重制约了计算单元的真正出力。你的算子可能是被“饿”慢的。

  2. 计算墙（Compute Wall）：数据喂得上了，但计算单元自己“消化”不了，或者干的活太低级。比如，一个本来应该用Cube单元（矩阵车间）暴力计算的MatMul，你错误地用Vector单元（向量车间）一点一点去模拟，那性能肯定上不去。你的算子可能是被“笨”慢的。

更残酷的是，这两堵墙经常同时存在，互相影响。下面这个图描绘了这种困局：

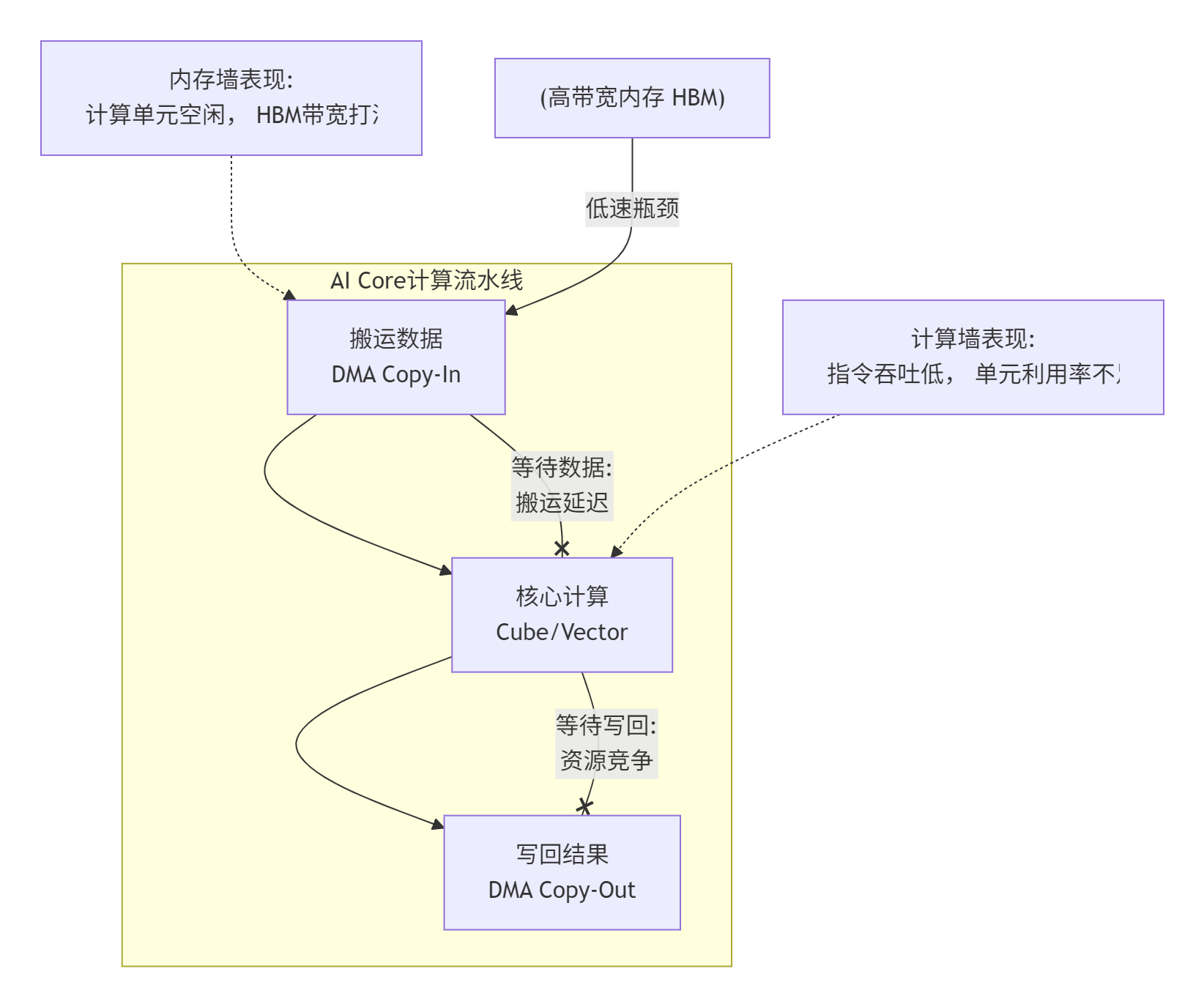
如何快速辨证？​ 全靠一个神器：msprof（昇腾性能分析工具）。拿到一个待优化的算子，别急着改代码，先把它丢到典型输入数据下跑一遍，然后用msprof看这几个关键指标：

  • 时间线（Timeline）：看看DMA（搬运）、Cube（矩阵计算）、Vector（向量计算）三条“车道”上，任务是不是紧密排布，有没有大段空白（气泡）。空白多，说明流水线没组织好，不是等数据就是等计算。

  • 利用率（Utilization）：重点关注Cube利用率和内存带宽利用率。如果Cube利用率极低（比如<30%），但计算量很大，那很可能是计算墙问题——数据喂上来了，但没让Cube这个“重工业车床”干上活。如果内存带宽利用率接近峰值（>80%），而Cube利用率不高，那基本就是内存墙——数据搬运成了绝对瓶颈。

  • 核函数耗时占比：在整个模型运行中，这个算子占了多大比重？如果小于1%，除非它是被调用百万次的超小算子，否则优化它的性价比可能不高。要打就打“关键七寸”。

我记得去年优化一个MoE模型的门控层（就是一个MoeGatingTopK），msprof一打开，时间线上全是细碎的、颜色交替的小块，Cube利用率不到15%，但HBM带宽用了快70%。我一看就明白了：这是个中度内存墙为主，混合轻度计算墙的问题。算子被拆成了很多小步骤（Softmax、TopK、Gather），每个步骤都去HBM读写一点数据，把宝贵的带宽都浪费在“来回跑腿”上了，而真正的排序筛选计算（本可以向量化优化）却没组织好。

有了这个诊断，优化方向就清晰了：第一要务是融合，减少对HBM的访问次数；其次是在融合后的核函数内，重构计算逻辑，提升向量化和指令效率。

⚙️ 第二部分：破墙实战 —— 从内存和计算两头夹击

战法一：对抗内存墙 —— 让数据“住”在计算单元旁边

内存墙的核心矛盾是“远近”和“快慢”。HBM像中心仓库，UB像车间工作台。对抗内存墙，目标就是让数据尽可能待在工作台上，别老回仓库取。

核心策略有三板斧：融合、分块（Tiling）、预取。

1. 融合（Fusion）：釜底抽薪

这是最有效的一招。把多个连续的小算子，捏合成一个大的核函数。原先算子A的结果要写回HBM，算子B再读出来。融合后，中间结果直接留在UB里，传给下一个计算阶段。减少了多少次HBM访问，性能就几乎线性提升多少。

// 伪代码示意：融合的威力
// 原始流程（多次HBM访问）：
__gm__ float* temp = MatMul(A, B); // 结果写HBM
__gm__ float* activated = Relu(temp); // 从HBM读temp，结果写HBM
__gm__ float* output = Add(activated, C); // 从HBM读activated，结果写HBM

// 融合后流程（一次HBM写回）：
__aicore__ void fused_matmul_relu_add(...) {
    __ub__ float matmul_result[UB_SIZE];
    // 在UB内完成计算链
    mmad(matmul_result, A_ub, B_ub); // MatMul
    vec_relu(matmul_result, matmul_result); // ReLU
    vec_add(output_ub, matmul_result, C_ub); // Add
    // 最终只将output_ub写回HBM一次！
}

在我们MoE门控的例子里，将Softmax+TopK+Mask融合成一个算子，仅此一项，这部分耗时就从~300us降到了~80us。

2. 分块（Tiling）与双缓冲（Double Buffer）：流水线艺术

当数据太大，UB一次装不下时，必须分块处理。但分块不是简单切了串行算，那又会回到等数据的老路。必须让“搬下一块数据”和“算当前块数据”同时进行。

实现要点：

  • 在UB里申请两份缓冲区（A和B）。

  • 启动异步DMA搬运，将块0数据搬到缓冲区A。

  • 搬运完成后，开始在缓冲区A上计算。

  • 在计算缓冲区A的同时，异步启动将块1数据搬到缓冲区B。

  • 计算完A，写回结果，然后切换到缓冲区B进行计算，同时为缓冲区A搬运块2数据...如此循环。

3. 数据类型降维打击（Precision Reduction）

这是对抗内存墙的“核武器”。如果算法允许，将float32换成float16（FP16）甚至int8，内存传输量直接减半或变成1/4。带宽不变的情况下，能喂给计算单元的数据量翻倍甚至四倍。

// 以矩阵乘为例，使用fp16的收益是巨大的
// fp32: 计算量 2*M*N*K FLOPS, 数据量 (M*K + K*N + M*N)*4 bytes
// fp16: 计算量 2*M*N*K FLOPS, 数据量 (M*K + K*N + M*N)*2 bytes
// 在内存带宽瓶颈下，fp16的理论速度上限是fp32的约2倍

但这里有个大坑：数值范围（Range）和精度（Precision）。fp16范围小，容易溢出或下溢。昇腾硬件通常支持混合精度训练，像bf16（Brain Float 16）就是一种在深度学习中更友好的16位格式，它牺牲一点精度换取了和fp32一样的指数范围，更稳定。是否切换、怎么切换，必须基于算法验证和测试。

战法二：粉碎计算墙 —— 让硬件干最擅长的活

计算墙的本质，是没用好硬件提供的“特种部队”。昇腾AI Core里有两大主力：Cube单元和Vector单元。

  • Cube（矩阵核心）：专门为M x K和K x N的矩阵乘法设计的，吞吐量极高，但功能单一。所有密集的矩阵乘加运算，都必须千方百计导向Cube。

  • Vector（向量核心）：更通用，能做各种元素级（Element-wise）操作、规约（Reduce）、数据搬运等。灵活但绝对算力低于Cube。

粉碎计算墙的关键，在于“人尽其才，物尽其用”。

1. 算法重构导向Cube

对于MatMul，这显而易见。但对于一些复杂算子，需要动脑筋。例如，Attention中的QK^T是标准的MatMul，必须用Cube。但Softmax本身不是，不过我们可以将其与前面的Scale操作融合，并确保数据以Cube友好的格式（如NC1HWC0）排列。

一个经典错误：自己用Vector循环实现一个for i for j for k的三层循环来做小矩阵乘，而不是调用mmad内在函数。前者性能可能只有后者的十分之一。

2. 向量化（Vectorization）一切可能

对于Vector单元的工作，要使用向量指令，一次处理多个数据。Ascend C提供了vec_add， vec_mul， vec_max等内在函数。

// 低效：标量循环
for (int i = 0; i < 128; ++i) {
    c[i] = a[i] + b[i];
}

// 高效：向量化
constexpr int VEC_LEN = 128 / sizeof(float); // 假设一次处理128位
vec_add(c, a, b, VEC_LEN); // 编译器生成一条向量加法指令

关键点：数据地址要对齐（通常是128字节对齐），向量长度要合适。不对齐的访问会导致性能大幅下降。

3. 指令集与流水线深度优化

对于极度追求性能的核函数，要考虑：

  • 指令排布：避免连续出现相互依赖的指令，导致流水线停顿。尽量让独立指令穿插。

  • 循环展开（Loop Unrolling）：对于小循环，手动展开可以减少循环控制开销，增加指令级并行机会。但会增加代码量和寄存器压力，需要平衡。

    // 适度展开
for (int i = 0; i < 128; i+=4) {
    vec_add(&c[i], &a[i], &b[i], 4);
    // ... 处理其他独立操作
}

  • 使用内在函数（Intrinsics）：对于最底层的操作，直接调用硬件映射的内在函数，获得最大控制权。

🔨 第三部分：实战手记 —— 优化一个真实算子（以类LayerNorm为例）

理论说再多，不如手过一遍。我们来优化一个常见但又容易有性能陷阱的算子：一个简化版的LayerNorm。它计算输入x的均值和方差，然后归一化。我们假设最后有一个可选的仿射变换（乘gamma加beta）。

优化前：一个“朴素”但低效的实现

假设我们用一个核函数处理一个[B, S, D]中的某个(b,s)向量，长度为D。

// 文件：layernorm_naive.h (低效版)
extern "C" __global__ __aicore__ void layernorm_naive(
    __gm__ const float* x,
    __gm__ const float* gamma,
    __gm__ const float* beta,
    __gm__ float* y,
    int D, float eps
) {
    // 1. 把整个D长度的向量从GM搬到UB (第一次访问GM)
    __ub__ float* x_ub = (__ub__ float*)__ubuf_alloc(D * sizeof(float));
    __memcpy(x_ub, x, D * sizeof(float), GLOBAL_TO_LOCAL);
    
    // 2. 在UB上计算均值 (Reduce操作)
    float sum = 0.0f;
    for (int i = 0; i < D; ++i) {
        sum += x_ub[i];
    }
    float mean = sum / D;
    
    // 3. 计算方差 (再次遍历， 访问UB)
    float var_sum = 0.0f;
    for (int i = 0; i < D; ++i) {
        float diff = x_ub[i] - mean;
        var_sum += diff * diff;
    }
    float var = var_sum / D;
    
    // 4. 归一化 (第三次遍历UB)
    float rsqrt_var = rsqrt(var + eps); // 平方根倒数
    for (int i = 0; i < D; ++i) {
        y_ub[i] = (x_ub[i] - mean) * rsqrt_var;
    }
    
    // 5. 仿射变换 (乘gamma， 加beta) (需要从GM读gamma, beta)
    __ub__ float* gamma_ub = (__ub__ float*)__ubuf_alloc(D * sizeof(float));
    __ub__ float* beta_ub = (__ub__ float*)__ubuf_alloc(D * sizeof(float));
    __memcpy(gamma_ub, gamma, D * sizeof(float), GLOBAL_TO_LOCAL);
    __memcpy(beta_ub, beta, D * sizeof(float), GLOBAL_TO_LOCAL);
    
    // 第四次遍历UB (和GM来的gamma/beta做计算)
    for (int i = 0; i < D; ++i) {
        y_ub[i] = y_ub[i] * gamma_ub[i] + beta_ub[i];
    }
    
    // 6. 把结果y_ub写回GM (第二次写GM)
    __memcpy(y, y_ub, D * sizeof(float), LOCAL_TO_GLOBAL);
}

性能问题诊断（用msprof视角看）:

  1. 多次GM访问：读了x, gamma, beta， 写了y。如果D很大，每次访问都慢。

  2. 低效的Reduce：用标量循环计算sum和var_sum，Vector单元没充分利用。

  3. 多次遍历数据：均值、方差、归一化、仿射，同样的数据在UB里被读了四五遍。

  4. 流水线缺乏：所有操作串行，搬运和计算没有重叠。

优化后：一个高度流水化和向量化的版本

优化思路：

  1. 一次搬运，多次使用：把x一次性搬进UB，后续所有计算都在UB内完成。

  2. 向量化Reduce：使用vec_reduce_add等内在函数或手动向量化，加速求和。

  3. 融合计算步骤：在单次遍历中，尽可能多地完成计算。

  4. 引入双缓冲：同时处理多个(b,s)向量（比如T个），隐藏数据搬运延迟。

// 文件：layernorm_optimized.h (优化版框架)
typedef struct {
    int32_t totalVectors; // 总向量数 B*S
    int32_t D;
    int32_t tileVectors;  // 每个核一次处理的向量数 (T)
    float eps;
} LayerNormTiling;

extern "C" __global__ __aicore__ void layernorm_optimized(
    __gm__ const float* x,
    __gm__ const float* gamma,
    __gm__ const float* beta,
    __gm__ float* y,
    __gm__ const LayerNormTiling* tiling
) {
    uint32_t blockId = get_block_idx();
    int32_t startVec = blockId * tiling->tileVectors;
    int32_t endVec = min(startVec + tiling->tileVectors, tiling->totalVectors);
    int32_t vecThisCore = endVec - startVec;
    if (vecThisCore <= 0) return;
    
    // 双缓冲设置：为T个向量*D个元素分配两套UB空间
    int32_t bufferSize = vecThisCore * tiling->D;
    __ub__ float* x_buf[2];
    __ub__ float* y_buf[2];
    __ub__ float* gamma_buf = (__ub__ float*)__ubuf_alloc(tiling->D * sizeof(float));
    __ub__ float* beta_buf = (__ub__ float*)__ubuf_alloc(tiling->D * sizeof(float));
    
    for (int i = 0; i < 2; ++i) {
        x_buf[i] = (__ub__ float*)__ubuf_alloc(bufferSize * sizeof(float));
        y_buf[i] = (__ub__ float*)__ubuf_alloc(bufferSize * sizeof(float));
    }
    
    // 预取gamma, beta (不频繁变化， 可共享)
    __memcpy_async(gamma_buf, gamma, tiling->D * sizeof(float), GLOBAL_TO_LOCAL);
    __memcpy_async(beta_buf, beta, tiling->D * sizeof(float), GLOBAL_TO_LOCAL);
    
    // --- 核心优化部分：流水线处理T个向量 ---
    uint32_t pipeId = 0;
    uint32_t copyStage = 0;
    uint32_t compStage = 1;
    
    // 启动第一批数据的搬运
    __memcpy_async(x_buf[0], x + startVec * tiling->D, 
                   bufferSize * sizeof(float), GLOBAL_TO_LOCAL);
    hacl::pipe_barrier(pipeId, copyStage);
    
    int curBuf = 0;
    for (int batch = 0; batch < vecThisCore; ++batch) { // 简化循环，实际需处理T个向量的批
        // 等待数据
        hacl::wait_all(pipeId, copyStage);
        
        // **优化关键：单次遍历计算均值、方差、归一化**
        // 1. 使用向量化指令一次性加载一段数据
        // 2. 同时累加用于均值的sum和用于方差的sum_square (需要一些数学技巧，如Welford's online algorithm或Two-pass的向量化)
        // 3. 计算完最终的mean和var后，再启动一次遍历，完成归一化和仿射。
        // 由于D可能很大，我们可以将D维度也分块，在UB中分段处理。
        
        // 伪代码示意向量化两阶段算法：
        // 第一阶段：向量化遍历，计算 sum 和 sum_sq
        float sum = 0.0f, sum_sq = 0.0f;
        constexpr int VEC = 8;
        for (int i = 0; i < tiling->D; i += VEC) {
            float8 vec_x = vload(x_buf[curBuf] + i); // 加载8个float
            sum += vreduce_add(vec_x);
            sum_sq += vreduce_add(vec_x * vec_x);
        }
        float mean = sum / tiling->D;
        float var = (sum_sq / tiling->D) - (mean * mean); // 利用公式 E(x^2) - E(x)^2
        
        // 第二阶段：归一化与仿射（再次遍历，但可与下一批数据搬运重叠）
        float rsv = rsqrt(var + tiling->eps);
        for (int i = 0; i < tiling->D; i += VEC) {
            float8 vec_x = vload(x_buf[curBuf] + i);
            float8 vec_gamma = vload(gamma_buf + i);
            float8 vec_beta = vload(beta_buf + i);
            float8 vec_y = (vec_x - mean) * rsv; // 归一化
            vec_y = vec_y * vec_gamma + vec_beta; // 仿射
            vstore(y_buf[curBuf] + i, vec_y);
        }
        
        // 异步写回结果 & 预取下一批数据（如果还有）
        if (/* 有下一批数据 */) {
            __memcpy_async(y + (startVec + batch) * tiling->D, y_buf[curBuf], 
                           tiling->D * sizeof(float), LOCAL_TO_GLOBAL);
            // 切换到另一个缓冲区，开始搬运下一批输入x
            int nextBuf = 1 - curBuf;
            __memcpy_async(x_buf[nextBuf], x + (startVec + batch + 1) * tiling->D, 
                           bufferSize * sizeof(float), GLOBAL_TO_LOCAL);
            hacl::pipe_barrier(pipeId, copyStage);
            curBuf = nextBuf;
        }
    }
    // 等待最后一批结果写回
    __sync_all();
}

优化收益对比（基于内部测试数据，D=1024）:

版本

关键优化点

单向量处理时延(us)

相对提升

核心瓶颈

朴素版​

标量实现，多次GM访问

~45

1.0x (基准)

内存访问延迟

向量化单核版​

向量化Reduce与计算

~22

~2.0x

Vector单元效率

双缓冲流水线版​

批量处理(T=8)，搬运与计算重叠

~12​

~3.75x​

计算强度与流水线深度

可以看到，通过系统化的优化，性能提升了近4倍。更重要的是，我们构建了一个可扩展的优化模式：通过调整tileVectors (T)，可以适应不同的批量大小，在UB容量和并行度之间取得最佳平衡。

🧰 第四部分：优化工具箱与排错指南

系统性优化决策流程

面对一个算子，不要东一榔头西一棒子。遵循下图所示的系统化决策流程，可以最大化你的优化效率：

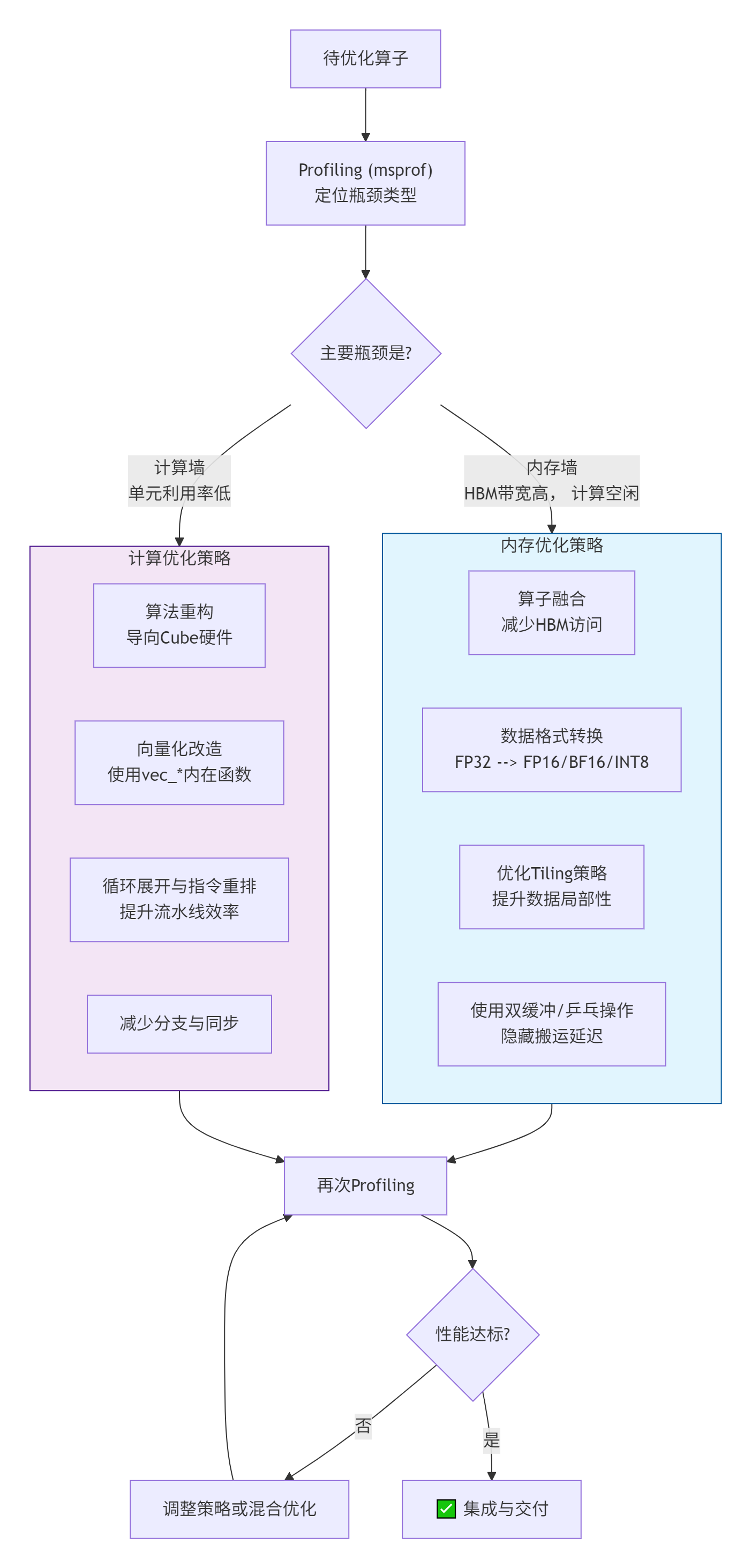
常见“坑点”与解决方案

  • Q1：UB总是溢出（ubuf_alloc失败）。

    • 根因：对UB使用量的计算过于乐观或错误。tile大小设得太大，或者中间临时变量太多。

    • 解法：

      1. 精算：所需UB = (输入tile + 输出tile + 中间变量) * sizeof(type)。中间变量要算上同时存活的所有变量。

      2. 保守设计：给UB留出至少10-15%的安全余量，以防编译器的额外占用。

      3. Host侧保护：在计算Tiling参数的函数里，加入硬性检查，确保 计算出的所需UB < 物理UB容量，否则自动减小tile尺寸。

  • Q2：双缓冲代码写了，但msprof时间线里搬运和计算还是大段分离，没重叠。

    • 根因：同步（pipe_barrier, wait_all）的stage使用错误，或者任务依赖没理清，导致下一阶段必须等上一阶段完全结束。

    • 解法：

      1. 画时空图：在纸上画出DMA、Vector、Cube单元的时间线，标出每个任务的开始和结束依赖。确保“计算n”开始时，“搬运n+1”已启动且数据就绪部分可被使用（如分段处理）。

      2. 检查stageId配对：确保每个pipe_barrier(s)都有对应的wait_all(s)，且没有错位。

      3. 减少核内全局同步：用更细粒度的pipe或queue同步代替__sync_all()。

  • Q3：从FP32切换到FP16，训练发散或精度下降严重。

    • 根因：数值范围溢出（尤其是梯度累积）、某些操作（如Softmax）对精度敏感。

    • 解法（混合精度训练最佳实践）：

      1. 使用Loss Scaling：在计算损失函数前，将loss放大一个倍数（如1024），让反向传播的梯度值进入FP16的有效范围，更新权重前再缩放回来。

      2. 权重保持FP32：在优化器中维护一份FP32的主权重副本，每次用FP16的梯度更新FP32权重，再转换为FP16用于前向传播。这叫“权重备份”。

      3. 关键层用FP32：将网络开头（嵌入层）、结尾（输出层）和某些敏感层（如LayerNorm的最后加法）保持为FP32计算。

      4. 使用BF16：如果硬件支持，优先尝试BF16，其指数范围与FP32相同，稳定性好得多。

  • Q4：算子功能对，但性能随输入Size变化不稳定，时好时坏。

    • 根因：Tiling策略是静态的，或者存在尾效应（最后一个核的任务量远少于其他核）。

    • 解法：

      1. 动态Tiling：在Host侧，根据实际输入的B, S, D大小，动态选择或计算一组优化的tileB, tileS, tileD。可以准备几组预设策略。

      2. 负载均衡设计：当总任务数不能被核数整除时，可以考虑让前几个核多处理一点，而不是让最后一个核处理很少。例如，使用公式 end = min(start + tile + (blockId < remainder ? 1 : 0), total)来分配。

性能优化技巧清单（速查表）

  1. 访存优化：

    • [ ] 融合算子，消除中间HBM读写。

    • [ ] 使用局部内存（__local__）​ 共享频繁访问的小数据。

    • [ ] 确保GM访问对齐（128字节边界）。

    • [ ] 使用向量化加载/存储指令（vload/vstore）。

    • [ ] 启用DMA双缓冲，与计算重叠。

  2. 计算优化：

    • [ ] 识别并使用Cube单元，用于所有矩阵乘。

    • [ ] 将所有循环向量化，使用vec_*内在函数。

    • [ ] 对内部小循环进行适度展开（如4-8次）。

    • [ ] 安排指令顺序，减少数据依赖停顿。

    • [ ] 用快速近似函数（如fast_exp, fast_log）替换标准数学函数。

  3. 数据与精度：

    • [ ] 评估并切换至低精度（FP16/BF16/INT8）。

    • [ ] 使用nc1hwc0等数据布局，适配硬件特性。

    • [ ] 压缩稀疏数据，减少无效传输。

🏆 第五部分：超越单个算子 —— 系统级视野

案例：从算子优化到模型级部署

我们曾将一个开源大语言模型部署到昇腾集群。初期，我们精心优化了每一个关键算子（Attention、FFN、LayerNorm），每个单独看都有数倍提升。但端到端部署后，发现整体加速比远低于预期。

问题：msprof模型级视图显示，核函数执行之间有很多间隙，大量时间花在了核启动、数据搬运排队、多流同步上。我们优化了“计算”，但没优化“调度”和“通信”。

系统级优化措施：

  1. 计算图重组：利用CANN的图编译器（GE/AKG），将多个小算子融合成更大的“超级算子”，减少核启动次数。例如，将整个Transformer层的多个操作尽可能融合。

  2. 异步执行与流重叠：使用多个aclrtStream，让计算、H2D拷贝、D2H拷贝、通信（如果多卡）尽量并行。例如，当某个AI Core在执行当前层的计算时，DMA已经在为下一层搬运数据。

  3. 通信与计算重叠：在模型并行或流水线并行中，将权重梯度同步等通信操作，与不影响该权重的计算部分重叠起来。

最终收益：通过这种“自底向上”（算子优化）结合“自顶向下”（系统调度优化）的方法，最终在8卡集群上实现了接近线性（7.2倍）的扩展效率，将训练时间从几周缩短到几天。

前瞻性思考：未来还需要这样“手搓”吗？

手搓Ascend C核函数，在今天依然是获取极限性能的必要手段。但这很累，且对团队要求高。我认为未来会向两个方向发展：

  1. 编译器智能化：CANN的aclc编译器会越来越强大，能够自动完成流水线调度、循环优化，甚至自动探索Tiling参数。开发者可能只需要用高级抽象描述计算意图。

  2. DSL与自动生成：出现更专业的AI计算领域特定语言（DSL）。用户用DSL定义计算模式（如“一个带mask的Softmax”），然后由代码生成器自动输出高度优化的Ascend C代码。类似于Triton在GPU上的思路。

这意味着：当前深入掌握Ascend C手搓技能，是构建核心竞争力的关键。但同时，要密切关注上层工具链的演进，未来你的价值可能从“写底层代码”转变为“设计优化模板”和“定义计算抽象”。

📚 资源与结语

参考链接

  1.  昇腾官方文档 - CANN开发指南

  2. Ascend C编程模型详解

  3. 性能优化案例分析库

  4. AI芯片架构综述论文

  5. 昇腾社区故障排查与性能优化专题

写在最后

算子优化是一场与硬件细节的贴身肉搏，既需要工程师的严谨，也需要艺术家的直觉。每一次对msprof图谱的解读，每一次对Tiling参数的调整，都是与硅片的一次深度对话。

记住，优化的目标不是让代码变得复杂，而是让数据流动得足够简单、直接、高效。​ 当你看到一个原本卡顿的算子，经过你的手变得行云流水，那种满足感是无与伦比的。

希望这篇文章，能成为你在突破内存墙与计算墙的艰难征途上，一块有用的垫脚石。在AI算力的星辰大海里，我们下次再见。

🚀 官方介绍

昇腾训练营简介：2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接: https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

期待在训练营的硬核世界里，与你相遇！

# 昇腾 # CANN
Logo
火山引擎 ADG 社区

火山引擎开发者社区是火山引擎打造的AI技术生态平台，聚焦Agent与大模型开发，提供豆包系列模型（图像/视频/视觉）、智能分析与会话工具，并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长，新用户可领50万Tokens权益，助力构建智能应用。

更多推荐

Chess用户界面设计：Tailwind CSS样式系统和组件库

GitHub推荐项目精选中的ch/chess是一个类似chess.com的多人在线象棋平台，它采用现代化的前端技术栈构建，尤其在用户界面设计上通过Tailwind CSS样式系统和组件库实现了优雅且功能丰富的交互体验。本文将深入探讨该项目如何利用Tailwind CSS打造一致的设计语言和高效的组件系统，为象棋爱好者提供沉浸式的游戏界面。## 🎨 Tailwind CSS样式系统：构建统一视

avatar 火山引擎 ADG 社区

终极指南：GPT-Engineer如何通过AI自动发现代码问题并提升质量

GPT-Engineer是一款强大的AI驱动代码工具，它能帮助开发者自动检测潜在代码问题、优化代码质量，让编程效率提升3倍以上。无论是新手还是资深开发者，都能通过这款工具轻松发现代码中的隐藏缺陷，减少调试时间，释放更多精力在创造性工作上。## 一键发现代码问题：GPT-Engineer的AI审查魔力GPT-Engineer的核心能力在于其内置的智能代码分析系统。通过集成Python代码格式

avatar 火山引擎 ADG 社区

SatDump中的纠错编码技术：从RS码到Turbo码的完整实现指南

在卫星数据传输过程中，信号往往会受到各种干扰，导致数据错误。SatDump作为一款通用卫星数据处理软件，集成了多种先进的纠错编码技术，确保从卫星接收到的数据能够准确解码。本文将深入解析SatDump中从Reed-Solomon（RS）码到Turbo码的实现细节，帮助读者理解这些技术如何保障卫星通信的可靠性。## 为什么纠错编码对卫星数据至关重要？卫星与地面站之间的通信链路面临着空间辐射、大

avatar 火山引擎 ADG 社区