背包加密

历史过程

背包加密是 1977 年由 Merkle 和 Hellman 提出的早期公钥加密算法，核心是借助背包问题的 “易解” 与 “难解” 特性构建加解密体系，曾为非对称加密提供重要思路，不过后来因被找到破解方法，安全性不足已逐步退出主流应用。

安全性缺陷：

该算法虽初期看似安全，但发布数年后被找到多种破解手段。比如 Shamir 提出的针对性破译方法，以及后来的 LLL 格基规约算法，都能高效破解这类加密。此外，若加密实现时参数选择不当（如超递增序列长度过短、模数 m 取值过小），攻击者还可通过枚举等方式获取密钥。正因这些缺陷，它逐渐被 RSA、ECC 等更安全的公钥算法取代，仅在加密原理教学等场景中仍有参考价值。

以下是其详细介绍：

引言

首先，我们先来介绍一下背包问题，假定一个背包可以称重 W，现在有 n 个物品，其重量分别为 a₁,a₂,…,a_n 我们想问一下装哪些物品可以恰好使得背包装满，并且每个物品只能被装一次。这其实就是在解这样的一个问题

​ x₁a₁+x₂a₂+,…,+x_na_n=W

其中所有的 x_i 只能为 0 和 1。显然我们必须枚举所有的 n 个物品的组合才能解决这个问题，而复杂度也就是 2ⁿ，这也就是背包加密的妙处所在。

超递增序列：本质是每一项都严格大于它之前所有项之和的正整数序列。

核心定义
序列中第 k 项（k≥2）的值，必须大于前 k-1 项所有元素的总和。公式表达：对序列 {a₁, a₂, ..., aₙ}，满足 aₖ > a₁ + a₂ + ... + aₖ₋₁（k 从 2 到 n）。
例子：
 {2，3，6，13，27，52}

核心原理

该算法的核心逻辑是区分两类背包问题并转化使用。

• 一类是基于超递增序列的易解背包问题（超递增序列指每一项都大于它之前所有项之和，如 {2，3，6，13，27，52}），这类问题可快速求解；

• 另一类是非超递增序列的难解背包问题，暴力破解需指数级时间。算法中，私钥对应易解的超递增背包序列，公钥则是通过模运算将超递增序列转化而来的难解普通序列。

加密时用公钥构造难解背包问题，解密时用私钥对应的易解背包问题还原明文，未掌握私钥者破解需攻克难解背包问题。

完整加解密流程

公私钥生成

生成私钥

私钥就是我们的初始的背包集，这里我们使用超递增序列。

生成公钥

在生成公钥的过程中主要使用了模乘的运算。

首先，我们生成模乘的模数m，这里要确保

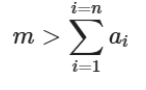
其次，我们选择模乘的乘数 w，作为私钥并且确保即 w 与 m 互质

gcd(w,m)=1 (最大公因数)

之后，我们便可以通过如下公式生成公钥

b_i≡wa_i mod m

并将这个新的背包集 bi 和 m 作为公钥。

加解密

加密

假设我们要加密的明文为 v，其每一个比特位为 v_i，那么我们加密的结果为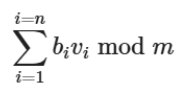

解密

对于解密方，首先可以求的 w 关于 m 的逆元 w⁻¹。

然后我们可以将得到的密文乘以 w⁻¹ 即可得到明文，这是因为

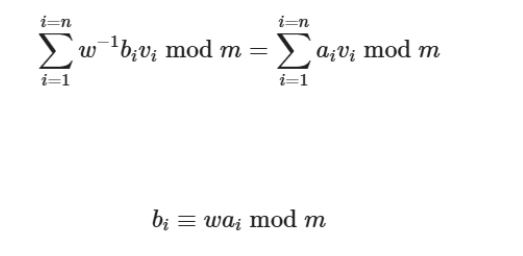
对于每一块的加密的消息都是小于 m 的，所以求得结果自然也就是明文了。

示例

以超递增序列 {2，3，6，13，27，52} 为例，具体步骤如下：

步骤	操作内容	举例说明
生成密钥	先确定私钥（超递增序列 {2，3，6，13，27，52}）；再选模数 m（需大于超递增序列总和，如 105）和乘数 w（需与 m 互质，如 31）；最后用 “（序列中每项 ×n）mod m” 生成公钥 {62,93,81,88,102,37}。	私钥：{2，3，6，13，27，52}、m=105、w=31；公钥：{62,93,81,88,102,37}
加密明文	将二进制明文按公钥序列长度分组，每组的二进制位对应公钥元素的取舍（1 取 0 舍），计算每组对应公钥元素的总和，得到密文。	明文分组 110101，对应取公钥中 62、93、88、37，总和 62+93+88+37=280，此 280 即为该分组的密文
解密密文	先计算乘数 w 的逆元 w⁻¹（满足 w×w⁻¹ ≡1 mod m，如 31 的逆元 61，31×61 mod105=1）；用 w⁻¹ 乘密文再对 m 取模，将密文还原为超递增序列对应的数值；最后通过超递增背包的求解方法，反向推出明文二进制。	密文 280×61 mod105=70，70 可拆分为 2+3+13+52，对应二进制 110101，还原明文分组

1. 分类与特点

背包加密主要分为加法背包和乘法背包两类，二者各有运算特点：

• 加法背包：序列满足 “前面所有数的和小于后面的数”，加密是计算选中元素的和。例如序列 {2，3，6，12，24，48}，密文 86 对应 2+12+24+48 的组合，未知序列时难以反向推导组合方式。
• 乘法背包：序列满足 “前面所有数的乘积小于后面的数”，加密计算选中元素的乘积。其数值增长远快于加法背包，加密后数据通常极大，但运算量也随之大幅增加。

参考文章

背包加密 - CTF Wiki

背包密码体制原理大白话讲解及Python实现-阿里云开发者社区