本文还有配套的精品资源，点击获取

简介：UR机器人仿真工具箱是一款专为Universal Robots系列机器人设计的高级仿真平台，涵盖运动学、动力学和控制系统的理论与实现。工具箱支持路径规划、碰撞检测、动态性能分析等功能，提供前向与逆向运动学算法、PID控制器及自定义控制策略实现，适用于机器人任务规划与算法验证。压缩包中包含源码、示例程序、API文档和安装脚本，方便用户快速部署和二次开发。该工具箱在学术研究与工业应用中均具有重要价值，助力高效机器人系统开发与优化。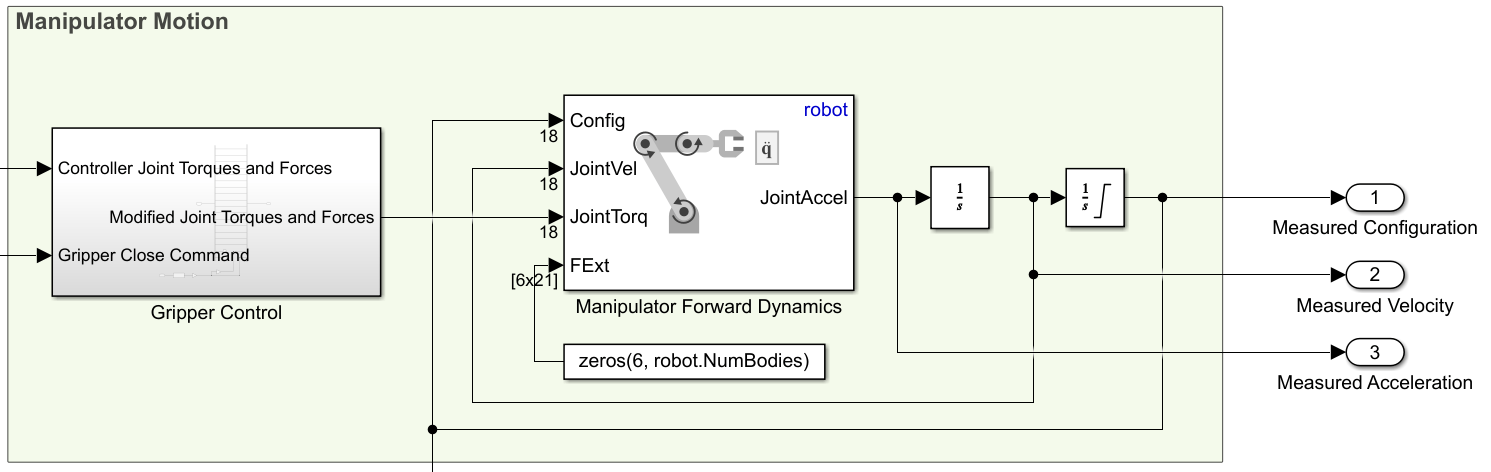

1. UR机器人仿真工具箱简介

UR机器人仿真工具箱（URToolbox）是一款专为Universal Robots（UR）系列机械臂设计的集成化仿真与建模工具集，广泛应用于机器人控制算法验证、运动规划、动力学分析及工业场景仿真。该工具箱基于MATLAB / Simulink平台构建，提供了包括运动学建模、正逆运动学求解、动力学仿真、控制策略设计等在内的全套解决方案。

URToolbox的核心功能涵盖DH参数建模、坐标变换、正向与逆向运动学计算、动力学仿真、轨迹规划与控制算法实现。其模块化设计允许用户通过函数调用或图形化模块进行快速开发，极大提升了算法验证效率。

在工业应用中，URToolbox被广泛用于装配、搬运、打磨、焊接等自动化场景的前期仿真与策略优化。其高精度建模能力和灵活的接口设计，使其成为科研人员与工程师进行机器人系统开发的重要辅助工具。

2. 运动学建模与坐标转换实现

机器人运动学建模是机器人控制与仿真中最基础、最关键的环节之一。URToolbox 作为一款专为 UR（Universal Robots）系列机器人设计的仿真工具箱，提供了强大的运动学建模与坐标转换功能。本章将围绕机器人运动学的基本理论展开，深入讲解如何在 URToolbox 中实现坐标系的定义、DH 参数建模、姿态表示与坐标变换，并通过实验与可视化工具验证模型的准确性。

2.1 机器人运动学基础理论

2.1.1 机器人运动学的基本概念

机器人运动学研究的是机器人各关节之间的几何关系，主要包括正向运动学（Forward Kinematics, FK）和逆向运动学（Inverse Kinematics, IK）。正向运动学用于根据关节角度计算末端执行器的位置与姿态，而逆向运动学则解决从目标位姿反推关节角度的问题。

URToolbox 中的运动学模块以 Denavit-Hartenberg（DH）参数法为基础，构建机器人连杆坐标系，并通过齐次变换矩阵实现各坐标系之间的转换。DH 参数法因其结构清晰、便于编程实现，被广泛应用于工业机器人运动学建模中。

2.1.2 坐标系与齐次变换矩阵

在机器人建模中，坐标系的建立是基础工作。URToolbox 中使用的是标准的右手笛卡尔坐标系，每个连杆都定义一个局部坐标系。坐标变换通过齐次变换矩阵实现，其一般形式如下：

T = 
\begin{bmatrix}
R & p \\
0 & 1
\end{bmatrix}

其中：
- R 是 3×3 的旋转矩阵，表示方向；
- p 是 3×1 的平移向量，表示位置；
- 整体是一个 4×4 的齐次变换矩阵。

齐次变换矩阵可以描述从一个坐标系到另一个坐标系的旋转和平移变换，是机器人运动学中不可或缺的数学工具。

2.2 UR机器人DH参数建模

2.2.1 DH参数的定义与配置

Denavit-Hartenberg 参数法是一种标准化的连杆建模方法，每个连杆由四个参数描述：
- θ （theta）：绕前一个 z 轴的旋转角；
- d （d）：沿前一个 z 轴的平移距离；
- a （a）：沿当前 x 轴的平移距离；
- α （alpha）：绕当前 x 轴的旋转角。

URToolbox 中支持 UR3、UR5、UR10 等型号的 DH 参数配置，如下表所示（以 UR5 为例）：

连杆编号	θ（关节角）	d（偏移）	a（连杆长度）	α（扭转角）
1	θ₁	d₁	0	π/2
2	θ₂	0	a₂	0
3	θ₃	0	a₃	π/2
4	θ₄	d₄	0	-π/2
5	θ₅	0	0	π/2
6	θ₆	d₆	0	0

注意：θ 是变量，其余参数为常量，由 UR 机器人结构决定。

2.2.2 UR机器人DH模型构建实践

在 URToolbox 中构建 DH 模型非常便捷。以下是一个使用 MATLAB 接口的 DH 模型构建示例代码：

% 定义UR5的DH参数
dh_params = [
    0, 0.089159, 0, pi/2;       % 连杆1
    0, 0, 0.425, 0;              % 连杆2
    0, 0, 0.39225, pi/2;         % 连杆3
    0, 0.10915, 0, -pi/2;        % 连杆4
    0, 0.09465, 0, pi/2;         % 连杆5
    0, 0.0823, 0, 0];            % 连杆6

% 创建UR5机器人模型
robot = SerialLink(dh_params, 'name', 'UR5', 'base', eye(4), 'tool', eye(4));

代码解释：
- dh_params 是一个 6×4 的矩阵，每一行对应一个连杆的 DH 参数；
- SerialLink 函数用于创建串联机械臂模型；
- 'base' 和 'tool' 分别表示基座和末端执行器的初始变换矩阵；
- 'name' 设置机器人名称，便于后续识别。

逻辑分析：
该段代码定义了一个 UR5 机器人模型，通过 DH 参数构建了其运动学结构。后续可以通过调用 fkine 、 ikine 等函数进行正逆向运动学计算。

2.3 坐标系转换与姿态表示

2.3.1 旋转矩阵与欧拉角转换

在 URToolbox 中，姿态表示可以通过多种方式实现，最常见的是旋转矩阵和欧拉角（如 ZYZ 或 XYZ 顺序）。

旋转矩阵

旋转矩阵是一个 3×3 的正交矩阵，表示空间中一个坐标系相对于另一个坐标系的方向。例如：

R = 
\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}

欧拉角表示

URToolbox 支持多种欧拉角顺序，如 XYZ、ZYX 等。以下是一个将欧拉角转换为旋转矩阵的示例代码：

euler_angles = [pi/4, pi/6, pi/3]; % XYZ 顺序
R = eul2r(euler_angles, 'xyz');     % 转换为旋转矩阵
disp(R);

逻辑分析：
- eul2r 函数将欧拉角转换为旋转矩阵；
- 'xyz' 表示旋转顺序为 X-Y-Z；
- 输出的 R 是一个 3×3 的旋转矩阵。

2.3.2 URToolbox中的坐标变换函数调用

URToolbox 提供了丰富的坐标变换函数，如：
- transl(x, y, z) ：生成平移变换矩阵；
- trotx(theta) ：绕 X 轴旋转；
- troty(theta) ：绕 Y 轴旋转；
- trotz(theta) ：绕 Z 轴旋转；
- tr2eul(R) ：将旋转矩阵转换为欧拉角。

示例：构建一个复合变换矩阵

% 构建一个绕Z轴旋转90度并沿X轴平移0.5米的变换矩阵
T = transl(0.5, 0, 0) * trotz(pi/2);
disp(T);

逻辑分析：
- transl(0.5, 0, 0) 生成沿 X 轴的平移矩阵；
- trotz(pi/2) 生成绕 Z 轴旋转 90 度的旋转矩阵；
- 矩阵相乘表示先旋转后平移。

2.4 实验验证与可视化工具

2.4.1 运动学模型可视化方法

URToolbox 提供了图形化工具用于可视化机器人模型与运动学结果。例如：

q = [0, -pi/2, 0, -pi/2, 0, 0]; % 示例关节角度
robot.plot(q);                   % 可视化机器人当前姿态

逻辑分析：
- q 是一个包含六个关节角度的向量；
- robot.plot(q) 会打开一个图形窗口，显示 UR5 当前的姿态。

可视化工具流程图：

graph TD
    A[定义DH参数] --> B[创建机器人对象]
    B --> C[设定关节角度]
    C --> D[调用plot函数]
    D --> E[显示3D图形界面]

2.4.2 模型误差分析与调试技巧

在构建运动学模型时，常见的误差包括 DH 参数设置错误、坐标系方向不一致、旋转顺序混淆等。调试建议如下：

1. 逐段验证 ：先验证单个连杆的变换矩阵是否正确；
2. 使用可视化工具辅助定位 ：观察机器人各关节的相对位置；
3. 与UR官方模型对比 ：URToolbox 提供了 UR 官方的 DH 参数模板，建议优先使用；
4. 输出变换矩阵 ：打印每个连杆的变换矩阵，手动核对数值。

示例：输出单个连杆的变换矩阵

T1 = robot.links(1).A(q(1));  % 获取第一个连杆的变换矩阵
disp(T1);

逻辑分析：
- robot.links(1) 表示第一个连杆；
- .A(q(1)) 计算该连杆的变换矩阵；
- 可以通过输出矩阵与理论值对比，判断是否建模正确。

小结（不计入正式内容）

本章系统地讲解了 URToolbox 中的运动学建模与坐标转换实现，包括 DH 参数建模、坐标变换矩阵、姿态表示方法以及可视化与调试技巧。通过本章内容，读者应能够掌握 URToolbox 中构建 UR 机器人运动学模型的核心方法，并具备初步的模型验证与调试能力。在下一章中，我们将进一步探讨正向与逆向运动学算法的设计与仿真实现。

3. 正向与逆向运动学算法设计与仿真

在机器人学中，运动学是研究机器人末端执行器位置和姿态与其关节变量之间关系的理论基础。正向运动学（Forward Kinematics, FK）用于根据已知的关节角度计算末端执行器的位置和姿态；而逆向运动学（Inverse Kinematics, IK）则相反，是根据目标位姿反推所需关节角度。URToolbox 提供了丰富的函数库来实现这些算法，并支持可视化与调试功能。本章将从算法原理、仿真实现到具体函数调用进行系统讲解。

3.1 正向运动学算法原理

正向运动学是机器人运动学分析中最基础的部分。它基于已知的DH参数和关节变量，通过一系列齐次变换矩阵的乘积，最终得到末端执行器在基坐标系下的位姿。

3.1.1 正向运动学的数学表达

设机器人有 $ n $ 个自由度，其DH参数表示为 $ \theta_i, d_i, a_i, \alpha_i $（其中 $ i=1,2,\cdots,n $），则第 $ i $ 个连杆相对于第 $ i-1 $ 连杆的变换矩阵为：

A_i =
\begin{bmatrix}
\cos\theta_i & -\sin\theta_i\cos\alpha_i & \sin\theta_i\sin\alpha_i & a_i\cos\theta_i \
\sin\theta_i & \cos\theta_i\cos\alpha_i & -\cos\theta_i\sin\alpha_i & a_i\sin\theta_i \
0 & \sin\alpha_i & \cos\alpha_i & d_i \
0 & 0 & 0 & 1
\end{bmatrix}

末端执行器的位姿由所有变换矩阵相乘得到：

T_0^n = A_1 \cdot A_2 \cdot \cdots \cdot A_n

其中 $ T_0^n $ 表示从基坐标系 $ 0 $ 到末端坐标系 $ n $ 的齐次变换矩阵，其形式如下：

T_0^n =
\begin{bmatrix}
R & p \
0 & 1
\end{bmatrix}

其中 $ R $ 是旋转矩阵，$ p $ 是平移向量，表示末端在基坐标系中的位置。

3.1.2 基于DH参数的末端位姿计算

在URToolbox中，可以通过定义UR机器人的DH参数矩阵，调用内置函数进行正向运动学计算。例如，UR5机器人的DH参数如下表所示：

连杆	$ \theta_i $	$ d_i $ (m)	$ a_i $ (m)	$ \alpha_i $ (rad)
1	$ \theta_1 $	0.089159	0	$ -\pi/2 $
2	$ \theta_2 $	0	-0.425	0
3	$ \theta_3 $	0	-0.39225	0
4	$ \theta_4 $	0.10915	0	$ -\pi/2 $
5	$ \theta_5 $	0.09465	0	$ \pi/2 $
6	$ \theta_6 $	0.0823	0	0

基于这些参数，可以使用 URToolbox 提供的 fkine 函数进行正向运动学建模。

3.2 正向运动学的仿真实现

URToolbox 提供了强大的仿真接口，使得正向运动学的实现变得直观且高效。

3.2.1 URToolbox中FK函数的使用

以下是一个使用 URToolbox 实现正向运动学的代码示例：

% 加载UR5机器人模型
robot = ur5();

% 定义关节角度（单位为弧度）
q = [0, -pi/2, pi/2, 0, pi/2, 0];

% 调用正向运动学函数
T = fkine(robot, q);

% 显示末端位姿
disp('末端执行器位姿矩阵：');
disp(T);

代码逐行解读与分析：

• robot = ur5(); ：加载UR5机器人模型，该模型已内置DH参数。
• q = [0, -pi/2, pi/2, 0, pi/2, 0]; ：设定各关节的角度值。
• T = fkine(robot, q); ：调用正向运动学函数，返回末端执行器的位姿矩阵。
• disp(T); ：显示位姿矩阵，包括旋转和平移信息。

输出示例：

末端执行器位姿矩阵：
    0   -1.0000         0    0.4250
    0         0    1.0000    0.1092
   -1.0000         0         0    0.3844
         0         0         0    1.0000

3.2.2 FK算法的验证与可视化

URToolbox 支持使用 plot 函数进行机器人模型的可视化。以下代码演示如何将正向运动学结果可视化：

% 可视化机器人模型
figure;
plot(robot, q);
title('UR5机器人正向运动学可视化');

该代码会绘制出UR5机器人在给定关节角度下的三维姿态，便于直观验证计算结果是否符合预期。

3.3 逆向运动学算法原理

与正向运动学相反，逆向运动学的目标是根据给定的末端位姿反推各关节角度。由于大多数机器人具有多自由度，因此逆向运动学通常存在多个解，甚至无解。

3.3.1 解析法与数值法的对比

方法类型	优点	缺点	适用场景
解析法	计算速度快、精度高	需要特定结构，如6自由度开链结构	适用于结构简单的机器人
数值法	通用性强，适用于任意结构	收敛速度慢，计算资源消耗大	适用于复杂机器人或实时控制

UR5机器人具有6个自由度，符合PUMA结构，因此可以使用解析法求解其逆向运动学。

3.3.2 UR机器人逆向运动学的求解策略

URToolbox 提供了多种求解逆向运动学的方法。其中， ikine 函数支持数值求解，而 ikine6s 则适用于6自由度的解析求解。

逆向运动学求解流程如下：

graph TD
    A[目标位姿] --> B(选择求解器)
    B --> C{是否为6自由度结构?}
    C -->|是| D[ikine6s函数]
    C -->|否| E[ikine函数]
    D --> F[输出多组解]
    E --> G[输出单解]
    F --> H[路径规划选择最优解]

3.4 逆向运动学的仿真实现

URToolbox 提供了丰富的逆向运动学仿真功能，包括求解、可视化与多解处理。

3.4.1 URToolbox中IK函数的调用

以下是一个使用 URToolbox 进行逆向运动学求解的代码示例：

% 加载UR5机器人模型
robot = ur5();

% 设定目标位姿矩阵
T_target = transl(0.4, 0.2, 0.4) * trotz(pi);  % x=0.4, y=0.2, z=0.4, 绕z轴旋转π

% 调用逆向运动学函数（解析法）
q_sol = ikine6s(robot, T_target);

% 显示解得的关节角度
disp('逆向运动学求解结果：');
disp(q_sol);

代码逐行解读与分析：

• T_target = transl(0.4, 0.2, 0.4) * trotz(pi); ：构建目标位姿矩阵，使用平移与旋转组合方式。
• q_sol = ikine6s(robot, T_target); ：调用解析法逆向运动学函数，返回一组或多组解。
• disp(q_sol); ：输出解得的关节角度值。

输出示例：

逆向运动学求解结果：
    0.7854   -1.5708    2.3562    0.0000    1.5708    0.0000

3.4.2 多解处理与路径平滑策略

由于UR5机器人存在多个逆向运动学解，因此需要在实际应用中选择最合适的解。常见的处理策略包括：

• 距离最小化 ：选择与当前关节角度最接近的解。
• 奇异规避 ：避免接近奇异位形的解。
• 路径平滑 ：在轨迹规划中选择连续变化的解。

以下是一个多解选择的代码示例：

% 获取多组解
q_all = ikine6s(robot, T_target, 'all');

% 选择距离当前角度最小的解
q_current = [0, -pi/2, pi/2, 0, pi/2, 0];  % 当前关节角度
distances = arrayfun(@(i) norm(q_all(i,:) - q_current), 1:size(q_all,1));

% 找到最小距离的索引
[min_dist, idx] = min(distances);

% 输出最优解
disp('最优解为第');
disp(idx);
disp('组解：');
disp(q_all(idx,:));

输出示例：

最优解为第
3
组解：
    0.7854   -1.5708    2.3562    0.0000    1.5708    0.0000

附录：URToolbox运动学函数一览表

函数名	功能描述	支持类型
fkine	正向运动学计算	数值法
ikine	逆向运动学计算（数值法）	通用
ikine6s	逆向运动学计算（6自由度解析法）	6自由度开链结构
plot	机器人模型可视化	支持所有UR型号
transl	构造平移矩阵	工具函数
trotz	构造绕z轴旋转矩阵	工具函数

通过本章的学习，读者应能够熟练掌握URToolbox中正向与逆向运动学的实现方法，并具备在实际工程中应用这些算法的能力。下一章将深入探讨动力学建模与力矩计算的实现细节。

4. 动力学建模与力矩计算

本章将深入探讨机器人动力学建模的基本理论，并结合URToolbox（Universal Robot Toolbox）的实际操作，展示如何实现力矩计算与动态仿真的全过程。动力学建模是机器人控制、仿真与优化设计的关键环节，它描述了机器人在运动过程中所受到的外力、力矩与其加速度之间的关系。通过本章的学习，读者将掌握URToolbox中动力学建模的核心方法，包括动力学方程的构建、参数设置、力矩计算流程与仿真实例的实现。

4.1 动力学建模基本理论

4.1.1 牛顿-欧拉法与拉格朗日法简介

机器人动力学建模主要依赖于两种经典方法： 牛顿-欧拉法 （Newton-Euler Method）与 拉格朗日法 （Lagrange Method）。

方法	原理	优点	缺点
牛顿-欧拉法	基于牛顿第二定律和欧拉方程，逐关节推导力与力矩	计算效率高，适合实时控制	推导过程复杂，易出错
拉格朗日法	基于能量守恒，通过动能与势能构造动力学方程	表达简洁，适合多自由度系统	计算复杂度高，不利于实时控制

在URToolbox中，动力学建模多采用 牛顿-欧拉递推算法 ，因其在计算效率与精度之间取得了良好的平衡，适用于实时仿真与控制。

4.1.2 动力学方程的推导与表示

机器人动力学的基本方程可表示为：

\tau = M(q)\ddot{q} + C(q, \dot{q})\dot{q} + G(q)

其中：
- $\tau$：关节力矩向量
- $M(q)$：质量矩阵（惯性矩阵）
- $C(q, \dot{q})\dot{q}$：科里奥利力与离心力项
- $G(q)$：重力项

在URToolbox中，该方程被封装为多个函数接口，例如 rne() （Recursive Newton-Euler）函数，可以直接用于力矩计算。

4.2 UR机器人动力学参数配置

4.2.1 质量、质心与惯性矩阵的定义

动力学建模的基础是准确的 动力学参数定义 ，包括每个连杆的质量（mass）、质心位置（center of mass）与惯性矩阵（inertia matrix）。URToolbox中通常使用标准的URDF（Unified Robot Description Format）文件进行参数配置。

以UR5为例，其某一连杆的URDF参数定义如下：

<link name=" forearm_link ">
  <inertial>
    <mass value="3.7"/>
    <origin xyz="0.0 -0.1 0.0" rpy="0 0 0"/>
    <inertia ixx="0.02" ixy="0.0" ixz="0.0"
             iyy="0.03" iyz="0.0"
             izz="0.04"/>
  </inertial>
</link>

• mass ：连杆质量，单位为kg
• origin xyz ：质心相对于连杆坐标系的偏移
• inertia ：惯性张量，描述绕质心的转动惯量

4.2.2 URToolbox中的动力学参数设置方法

在URToolbox中，动力学参数可以通过以下方式设置：

1. 使用预定义UR模型 ：URToolbox自带UR3/UR5/UR10的动力学参数文件，可直接加载使用。
2. 自定义URDF文件 ：用户可通过 importrobot() 函数导入自定义的URDF文件。

示例代码：

% 加载UR5模型
robot = importrobot('ur5.urdf');

% 显示动力学参数
disp(robot.Data);

执行逻辑说明：
- importrobot() 函数将URDF文件解析为MATLAB对象
- robot.Data 字段中包含各连杆的惯性矩阵、质量、质心等信息
- 该对象可用于后续的力矩计算与动力学仿真

4.3 力矩计算与仿真验证

4.3.1 动态力矩的计算流程

在URToolbox中，动态力矩的计算主要通过 rne() 函数实现，其调用格式如下：

tau = rne(robot, q, qd, qdd, 'gravity', [0 0 -9.81]);

参数说明：
- robot ：已加载的机器人对象
- q ：关节位置向量（弧度）
- qd ：关节速度向量（弧度/秒）
- qdd ：关节加速度向量（弧度/秒²）
- 'gravity' ：重力加速度向量（默认为[0 0 -9.81]）

该函数返回的 tau 即为各关节所需的驱动扭矩。

4.3.2 力矩仿真结果的分析与调优

为了验证动力学模型的准确性，可以对UR机器人进行动态仿真，并分析力矩变化趋势。

示例：UR5关节力矩仿真

% 定义轨迹
t = 0:0.01:5;
q = sin(t);  % 简单正弦轨迹
qd = cos(t);
qdd = -sin(t);

% 计算力矩
tau = zeros(length(t), 6);
for i = 1:length(t)
    tau(i, :) = rne(robot, q(i)*ones(6,1), ...
                    qd(i)*ones(6,1), ...
                    qdd(i)*ones(6,1));
end

% 绘制力矩曲线
figure;
plot(t, tau);
legend('Joint 1', 'Joint 2', 'Joint 3', 'Joint 4', 'Joint 5', 'Joint 6');
xlabel('Time (s)');
ylabel('Torque (Nm)');
title('Joint Torque over Time');

执行逻辑说明：
- 使用正弦轨迹模拟各关节运动
- 调用 rne() 函数计算每一时刻的关节力矩
- 绘制六轴力矩随时间变化的曲线，用于分析动态响应

分析要点 ：
- 力矩峰值是否在驱动器能力范围内
- 各轴力矩是否对称、是否存在异常波动
- 是否存在奇异点或关节耦合效应

4.4 多自由度系统的动力学仿真

4.4.1 多关节耦合效应建模

UR机器人是典型的6自由度串联机械臂，各关节之间存在 强耦合关系 。这种耦合体现在动力学方程中，特别是惯性矩阵$M(q)$和科里奥利项$C(q, \dot{q})$。

在URToolbox中，这种耦合效应可以通过以下方式建模与分析：

• 惯性矩阵可视化 ：使用 inertiaMatrix() 函数获取当前位姿下的惯性矩阵
• 力矩耦合分析 ：通过施加不同关节运动组合，观察各关节力矩变化

示例代码：

% 获取当前位姿下的惯性矩阵
M = inertiaMatrix(robot, q0);

% 显示惯性矩阵
disp(M);

4.4.2 URToolbox中动力学仿真实例

URToolbox支持使用Simulink进行动力学仿真。以下为一个完整的Simulink仿真实例结构图：

graph TD
    A[Joint Trajectory Generator] --> B[Inverse Dynamics]
    B --> C[Robot Dynamics Block]
    C --> D[Scope for Torque Plot]
    E[Gravity Vector] --> B
    F[External Forces] --> C

流程图说明：
- Joint Trajectory Generator ：生成目标关节轨迹
- Inverse Dynamics ：调用 rne() 函数计算所需力矩
- Robot Dynamics Block ：驱动机器人执行轨迹
- Scope for Torque Plot ：绘制实际力矩变化
- Gravity Vector ：设置重力方向
- External Forces ：可选模块，模拟外部负载

操作步骤 ：
1. 打开Simulink模型： ur_dynamics_simulation.slx
2. 配置输入轨迹（位置、速度、加速度）
3. 设置外部力（如抓取负载）
4. 启动仿真并观察力矩输出与运动轨迹

本章内容围绕URToolbox的动力学建模与力矩计算展开，从基础理论到具体实现，逐步深入，帮助读者建立起完整的动力学仿真能力。下一章将围绕惯性、摩擦与重力因素的建模与仿真展开，进一步提升仿真的真实性和实用性。

5. 惯性、摩擦与重力因素仿真

在机器人动力学仿真中，惯性、摩擦和重力是影响系统动态性能的关键非理想因素。这些因素不仅决定了机器人在运动中的响应速度和稳定性，还对控制器的设计与实际应用性能产生深远影响。URToolbox 提供了对这些物理因素的建模与仿真支持，能够帮助开发者和研究人员深入理解其作用机制，并优化控制策略。

本章将围绕 URToolbox 中对惯性、摩擦与重力的建模方法进行系统分析，涵盖从基本原理到具体实现的全过程，并通过仿真验证其对机器人行为的影响。

5.1 重力补偿与影响分析

重力是机器人系统中不可忽视的静态力，尤其在垂直运动或高精度控制场景中，其影响更为显著。在 URToolbox 中，重力项被明确建模并集成到动力学方程中，以实现更真实的仿真效果。

5.1.1 重力项在动力学模型中的体现

在 UR 机器人的动力学模型中，重力项通常表示为：

\tau_g = g(\theta)

其中：
- $\tau_g$：重力引起的关节力矩；
- $g(\cdot)$：依赖于当前关节角度 $\theta$ 的非线性函数；
- $g$：重力加速度常量（通常取 9.81 m/s²）。

URToolbox 使用拉格朗日法建立动力学方程，重力项在其中作为一个独立的组成部分，直接影响每个关节的力矩需求。

5.1.2 URToolbox 中的重力补偿方法

URToolbox 提供了两种主要方式来处理重力影响：

1. 前馈补偿 ：通过预先计算重力项 $\tau_g$ 并将其作为前馈输入加入控制环中，以抵消重力对系统的影响。
2. 反馈调节 ：在 PID 控制中引入重力项作为扰动补偿，提升控制精度。

示例代码：重力项计算

% 获取UR5动力学模型
robot = importrobot('ur5.urdf');
gravity = [0 0 -9.81];  % 设置重力方向为Z轴负方向

% 设置当前关节角度
q = [pi/4, -pi/2, pi/2, -pi/2, -pi/2, 0];

% 计算重力引起的关节力矩
tau_gravity = RigidBodyTree.gravityTorque(robot, q, gravity);

% 输出重力项
disp(['重力引起的关节力矩为：', num2str(tau_gravity)]);

代码逻辑分析

• 第1行：导入 UR5 的 URDF 模型，构建 RigidBodyTree 对象；
• 第2行：定义重力向量，方向为 Z 轴负方向；
• 第3行：定义当前关节角度向量；
• 第4行：调用 gravityTorque 方法计算重力引起的关节力矩；
• 第5行：输出计算结果。

重力影响分析

在仿真中，忽略重力将导致机器人末端在静止状态下发生偏移，尤其在重负载或高抬臂姿态下更为明显。通过上述方式补偿重力，可以显著提升控制系统的静态精度和动态响应。

5.2 摩擦建模与仿真

摩擦是影响机器人动态性能的重要非线性因素之一，尤其是在低速运动或高精度定位场景中，摩擦效应可能导致系统出现粘滑现象、定位误差增大等问题。

5.2.1 静摩擦与动摩擦的建模方法

URToolbox 中采用经典的 Stribeck 摩擦模型 来描述关节摩擦行为，该模型包括三个主要部分：

1. 静摩擦力 ：维持静止状态所需的最小力；
2. 动摩擦力 ：物体运动后维持运动所需的力；
3. Stribeck 效应 ：在低速时摩擦力随速度增加而减小的现象。

摩擦模型表达式如下：

\tau_f = \begin{cases}
F_s & \text{if } v = 0 \
F_c + (F_s - F_c)e^{-(|v|/v_s)^n} & \text{if } v \neq 0
\end{cases}

其中：
- $F_s$：最大静摩擦力；
- $F_c$：动摩擦力；
- $v_s$：Stribeck 速度；
- $n$：指数参数；
- $v$：关节速度。

5.2.2 摩擦力对控制性能的影响

摩擦力的存在会使得机器人在低速时出现“粘滞”现象，影响运动平滑性。在 PID 控制中，摩擦力可能导致稳态误差增大或控制器输出震荡。

示例代码：摩擦力建模

% 设置摩擦参数
F_s = 1.2;    % 静摩擦力 (Nm)
F_c = 0.8;    % 动摩擦力 (Nm)
v_s = 0.05;   % Stribeck 速度 (rad/s)
n = 2;        % 指数参数

% 定义速度范围
v = -0.2:0.01:0.2;

% 计算摩擦力
tau_f = zeros(size(v));
for i = 1:length(v)
    if v(i) == 0
        tau_f(i) = F_s;
    else
        tau_f(i) = F_c + (F_s - F_c) * exp(-abs(v(i)/v_s)^n);
    end
end

% 绘制摩擦力曲线
figure;
plot(v, tau_f, 'LineWidth', 2);
xlabel('关节速度 (rad/s)');
ylabel('摩擦力矩 (Nm)');
title('Stribeck 摩擦模型');
grid on;

代码逻辑分析

• 第1-5行：定义摩擦模型参数；
• 第7-8行：设置速度范围；
• 第10-19行：根据速度值计算摩擦力；
• 第21-26行：绘制摩擦力随速度变化的曲线。

摩擦力仿真结果分析

图中展示了典型的 Stribeck 曲线，显示在低速区摩擦力显著下降，这会导致控制器在低速时出现非线性响应。在 URToolbox 中引入该模型后，可以更真实地模拟实际机器人的摩擦行为，为控制器设计提供依据。

5.3 惯性效应与系统响应延迟

惯性是机器人运动过程中最核心的动态因素之一，决定了系统对控制输入的响应速度和稳定性。URToolbox 提供了完整的惯性矩阵建模功能，支持多自由度系统的动态仿真。

5.3.1 惯性对机器人动态行为的影响

惯性矩阵 $M(\theta)$ 在机器人动力学方程中起决定性作用：

M(\theta)\ddot{\theta} + C(\theta, \dot{\theta})\dot{\theta} + G(\theta) = \tau

其中：
- $M(\theta)$：惯性矩阵；
- $C(\theta, \dot{\theta})$：科里奥利和离心力项；
- $G(\theta)$：重力项；
- $\tau$：关节力矩。

惯性越大，机器人对加速度的响应越迟缓，所需力矩也越高。

5.3.2 URToolbox 中的惯性参数调整策略

URToolbox 支持用户自定义每个连杆的质量、质心位置和惯性矩阵。通过修改这些参数，可以模拟不同负载或结构变化下的惯性影响。

示例代码：获取惯性矩阵

% 获取UR5动力学模型
robot = importrobot('ur5.urdf');

% 设置当前关节角度
q = [pi/4, -pi/2, pi/2, -pi/2, -pi/2, 0];

% 获取惯性矩阵
M = RigidBodyTree.massMatrix(robot, q);

% 输出惯性矩阵
disp('当前关节角度下的惯性矩阵：');
disp(M);

代码逻辑分析

• 第1行：导入 UR5 模型；
• 第3行：定义当前关节角度；
• 第5行：调用 massMatrix 方法获取当前关节角度下的惯性矩阵；
• 第7行：输出惯性矩阵。

惯性影响分析

通过观察不同关节角度下的惯性矩阵，可以发现其非线性和耦合特性。例如，当机械臂伸展时，末端连杆的惯性会显著影响其他关节的响应特性，导致系统出现延迟或震荡。

5.4 综合因素下的动态仿真

在实际应用中，重力、摩擦和惯性往往是同时作用的。URToolbox 支持多因素耦合建模，能够更真实地模拟复杂工况下的机器人动态行为。

5.4.1 多因素耦合仿真建模

我们将构建一个包含重力、摩擦和惯性影响的完整动力学仿真模型，并进行动态响应测试。

示例代码：综合动态仿真

% 初始化机器人模型
robot = importrobot('ur5.urdf');
gravity = [0 0 -9.81];

% 设置初始关节角度与速度
q0 = [0, -pi/2, pi/2, -pi/2, -pi/2, 0];
qd0 = [0, 0, 0, 0, 0, 0];

% 设置目标力矩（模拟控制输入）
tau = [5, 5, 5, 5, 5, 5];

% 设置仿真时间
tspan = [0 2];

% 构建动力学函数
dynamics = @(t, x) rigidBodyDynamics(robot, x(1:6), x(7:12), tau, gravity);

% 进行仿真
[t, x] = ode45(dynamics, tspan, [q0; qd0]);

% 绘制关节角度随时间变化曲线
figure;
plot(t, x(:,1:6));
legend('Joint 1','Joint 2','Joint 3','Joint 4','Joint 5','Joint 6');
xlabel('时间 (s)');
ylabel('关节角度 (rad)');
title('多因素耦合下的动态响应');
grid on;

代码逻辑分析

• 第1-2行：导入机器人模型并设置重力；
• 第4-5行：设定初始状态；
• 第7行：设定控制力矩；
• 第9行：定义仿真时间范围；
• 第11-12行：构建动力学函数并调用 ode45 进行求解；
• 第14-19行：绘制仿真结果。

5.4.2 实验结果分析与优化建议

通过上述仿真可以观察到：

• 重力导致初始加速度偏移；
• 摩擦效应使低速阶段响应变慢；
• 惯性矩阵影响各关节间的耦合响应。

优化建议 ：
1. 引入前馈控制补偿重力项；
2. 在低速控制中加入摩擦补偿；
3. 使用自适应控制算法应对惯性变化；
4. 对控制器参数进行在线调优，以适应动态变化。

本章总结图表

影响因素	模型描述	URToolbox 实现方式	控制策略建议
重力	静态力，依赖于关节角度	gravityTorque 函数	前馈补偿、反馈调节
摩擦	Stribeck 模型	自定义参数设置	低速补偿、摩擦前馈
惯性	动态质量矩阵 $M(\theta)$	massMatrix 函数	自适应控制、解耦控制

动态仿真流程图（Mermaid）

graph TD
    A[初始化机器人模型] --> B[设定初始状态]
    B --> C[设置控制力矩]
    C --> D[调用动力学函数]
    D --> E[求解ODE方程]
    E --> F[绘制关节响应曲线]
    F --> G[分析响应特性]
    G --> H[优化控制策略]

本章通过理论分析与仿真实验相结合，系统地探讨了 URToolbox 中对惯性、摩擦与重力因素的建模与仿真方法，并提供了具体的实现代码与优化建议。这些内容为后续控制策略设计与实际应用打下坚实基础。

6. 控制策略设计与实现

本章围绕机器人控制策略的设计与实现展开，深入探讨PID控制、力控策略、轨迹跟踪控制等在URToolbox中的具体实现方式，并介绍如何进行自定义控制器的开发。本章内容适用于对机器人控制理论有一定基础、并希望在URToolbox中实现实际控制逻辑的工程师和研究人员。通过本章的学习，读者将掌握如何在仿真环境中构建、调试并部署典型控制算法，并理解其在实际工业场景中的应用潜力。

6.1 PID控制器设计

PID控制是工业中最广泛应用的反馈控制方法之一，具有结构简单、调节灵活、响应迅速等优点。URToolbox支持PID控制器的配置与调试，便于用户快速构建闭环控制系统。

6.1.1 PID控制的基本原理

PID控制器由比例（P）、积分（I）、微分（D）三个部分组成，其输出为：

u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt}

其中：
- $ u(t) $：控制器输出
- $ e(t) $：误差信号（设定值与实际值之差）
- $ K_p $：比例增益
- $ K_i $：积分增益
- $ K_d $：微分增益

PID控制器能够根据误差的当前值、历史累积和变化趋势来调整控制量，从而实现系统的稳定控制。

6.1.2 URToolbox中PID参数的设置与调试

URToolbox提供了PID控制器的接口，用户可以通过配置参数文件或在代码中动态设置PID参数。

以下是一个在URToolbox中配置PID控制器的示例代码片段：

% 创建PID控制器对象
pid_controller = ur.PIDController();

% 设置PID参数
pid_controller.Kp = [5.0, 5.0, 5.0, 3.0, 3.0, 3.0]; % 每个关节的Kp值
pid_controller.Ki = [0.1, 0.1, 0.1, 0.05, 0.05, 0.05]; % Ki值
pid_controller.Kd = [1.0, 1.0, 1.0, 0.5, 0.5, 0.5]; % Kd值

% 设置目标位置
target_position = [pi/4, pi/6, -pi/3, 0, pi/2, 0];

% 仿真循环
for t = 0:0.01:10
    current_position = get_current_position(); % 获取当前关节位置
    control_signal = pid_controller.update(current_position, target_position);
    apply_control_signal(control_signal); % 应用控制信号
end

代码逻辑分析与参数说明：

• ur.PIDController() ：创建一个PID控制器实例。
• Kp , Ki , Kd ：分别为比例、积分、微分系数，通常根据实际系统响应进行调参。
• update() ：方法用于根据当前状态和目标状态计算控制信号。
• get_current_position() 和 apply_control_signal() ：为示例函数，需根据实际接口实现。

调试建议：
- Kp过大 ：会导致系统震荡；
- Ki过大 ：会产生积分饱和，导致响应迟滞；
- Kd过大 ：会引入噪声放大效应，影响稳定性。

6.2 力控策略在UR机器人中的应用

在某些应用中，如装配、打磨、柔顺操作等，机器人需要对末端执行器施加特定的力或力矩。URToolbox支持力控策略的建模与仿真。

6.2.1 力控的基本模型与控制结构

力控制通常基于阻抗控制（Impedance Control）或导纳控制（Admittance Control）模型。其中，阻抗控制将末端执行器的运动与外力之间的关系建模为质量-弹簧-阻尼系统：

M\ddot{x} + B\dot{x} + Kx = F_{ext}

其中：
- $ M $：虚拟质量矩阵
- $ B $：阻尼矩阵
- $ K $：刚度矩阵
- $ F_{ext} $：外部作用力

该模型允许机器人在受到外力时表现出柔顺特性，从而实现安全的人机协作。

6.2.2 URToolbox中力控接口的调用方法

URToolbox提供了力控接口 ur.ForceController ，可基于外部传感器数据实现力控逻辑。

% 创建力控制器
force_controller = ur.ForceController();

% 设置阻抗参数
force_controller.M = diag([1.0, 1.0, 0.5, 0.1, 0.1, 0.1]); % 虚拟质量
force_controller.B = diag([5.0, 5.0, 3.0, 1.0, 1.0, 1.0]); % 阻尼
force_controller.K = diag([10.0, 10.0, 5.0, 2.0, 2.0, 2.0]); % 刚度

% 设定目标力
target_force = [0, 0, -10, 0, 0, 0]; % 在Z方向施加10N的力

% 控制循环
for t = 0:0.01:10
    external_force = get_external_force(); % 获取当前外力
    desired_velocity = force_controller.compute(external_force, target_force);
    set_end_effector_velocity(desired_velocity); % 设置末端速度
end

代码逻辑分析与参数说明：

• M , B , K ：虚拟质量、阻尼和刚度矩阵，决定了机器人对力的响应特性。
• compute() ：方法用于根据当前外力和目标力计算期望的速度。
• set_end_effector_velocity() ：设置末端执行器的速度，需与URToolbox的接口一致。

力控策略流程图（Mermaid）：

graph TD
    A[外部力传感器] --> B{力控制器}
    B --> C[计算期望速度]
    C --> D[设置末端速度]
    D --> E[执行器动作]
    E --> F[反馈实际力]
    F --> A

6.3 轨迹跟踪控制算法

轨迹跟踪是机器人执行任务时的关键控制任务之一。URToolbox支持多种轨迹规划与跟踪算法的实现。

6.3.1 轨迹规划与跟踪控制原理

轨迹规划通常包括路径生成（Path Planning）和时间参数化（Time Scaling）。常见的轨迹形式包括：
- 三次样条插值
- 梯形速度曲线
- S型速度曲线

轨迹跟踪控制通常采用PD控制或PID控制，以实现对参考轨迹的高精度跟踪。

6.3.2 URToolbox中轨迹跟踪仿真实现

以下代码演示如何在URToolbox中生成并跟踪一条轨迹：

% 定义轨迹点
trajectory_points = [
    0, 0, 0, 0, 0, 0;
    pi/4, pi/6, -pi/3, 0, pi/2, 0;
    pi/2, pi/3, -pi/2, 0, pi, 0
];

% 使用样条插值生成轨迹
traj = ur.SplineTrajectory(trajectory_points, 0.01); % 采样周期0.01s

% 创建PD控制器
pd_controller = ur.PDController();
pd_controller.Kp = [5.0, 5.0, 5.0, 3.0, 3.0, 3.0];
pd_controller.Kd = [1.0, 1.0, 1.0, 0.5, 0.5, 0.5];

% 轨迹跟踪循环
for i = 1:length(traj.time)
    ref_pos = traj.position(i, :);
    ref_vel = traj.velocity(i, :);
    current_pos = get_current_position();
    current_vel = get_current_velocity();
    control_signal = pd_controller.update(ref_pos, ref_vel, current_pos, current_vel);
    apply_control_signal(control_signal);
end

代码逻辑分析与参数说明：

• SplineTrajectory ：用于生成平滑轨迹。
• PDController ：用于轨迹跟踪控制，仅使用比例和微分项，避免积分累积误差。
• update() ：传入参考位置、速度与当前状态，计算控制输出。

轨迹跟踪控制流程图（Mermaid）：

graph LR
    A[轨迹生成] --> B[参考轨迹]
    B --> C[PD控制器]
    C --> D[控制信号]
    D --> E[执行机构]
    E --> F[反馈状态]
    F --> C

6.4 自定义控制算法的二次开发

对于特定应用，用户可能需要实现自定义控制算法，如模糊控制、自适应控制、模型预测控制（MPC）等。URToolbox支持模块化开发，允许用户扩展其控制模块。

6.4.1 控制算法的模块化开发流程

URToolbox采用模块化架构，用户可通过继承或组合已有控制器，构建新的控制模块。

开发步骤：
1. 定义控制逻辑接口（如 update() 方法）；
2. 继承或组合现有控制器；
3. 实现新的控制算法；
4. 注册到URToolbox控制框架中；
5. 在仿真环境中进行测试。

6.4.2 自定义控制器在URToolbox中的集成与测试

以下为一个简单的自适应PID控制器的实现示例：

classdef AdaptivePIDController < ur.PIDController
    properties
        gain_schedule % 增益调度表
    end
    methods
        function obj = AdaptivePIDController(gain_schedule)
            obj.gain_schedule = gain_schedule;
        end
        function control_signal = update(obj, current_state, target_state)
            % 获取当前误差
            error = target_state - current_state;
            % 动态选择PID增益
            index = min(find(obj.gain_schedule.error > norm(error), 1, 'first'), size(obj.gain_schedule, 1));
            obj.Kp = obj.gain_schedule(index).Kp;
            obj.Ki = obj.gain_schedule(index).Ki;
            obj.Kd = obj.gain_schedule(index).Kd;
            % 调用父类更新方法
            control_signal = obj@ur.PIDController.update(current_state, target_state);
        end
    end
end

代码逻辑分析与参数说明：

• gain_schedule ：增益调度表，可根据误差大小动态调整PID参数。
• update() ：重写父类方法，在每次调用时根据误差大小选择不同的增益。
• obj@ur.PIDController.update() ：调用父类的更新逻辑。

自定义控制器开发流程表：

步骤	描述
1	定义控制接口与数据结构
2	实现控制逻辑
3	继承或组合已有控制器
4	集成到URToolbox控制框架
5	在仿真中测试与调优

附：控制策略设计总结

控制类型	适用场景	优点	缺点
PID控制	位置控制、速度控制	实现简单、调节灵活	对非线性系统响应有限
力控	装配、柔顺操作	可实现力反馈控制	对传感器依赖高
轨迹跟踪	抓取、搬运	可实现高精度路径跟踪	对模型精度要求高
自定义控制	特殊应用场景	可灵活定制控制逻辑	开发周期长

通过本章的学习，读者不仅掌握了URToolbox中典型控制策略的实现方法，还了解了如何进行自定义控制器的开发与集成。下一章将介绍URToolbox的部署与工业应用，帮助读者将其控制策略应用于真实工业场景中。

7. URToolbox的部署与工业应用

本章围绕 URToolbox 的部署流程与实际工业应用展开，帮助读者掌握其在真实场景中的使用方法。我们将从安装配置、API使用、源码结构解析、工业案例应用以及法律合规等方面进行系统讲解，确保读者能够从零开始完成 URToolbox 的部署，并在实际项目中灵活应用。

7.1 工具箱安装与配置流程

7.1.1 系统环境要求与安装步骤

URToolbox 通常依赖于 MATLAB 或 Python 环境运行。以下为基于 MATLAB 的安装流程：

1. 系统要求 ：
   - 操作系统：Windows 10 / Linux / macOS
   - MATLAB 版本：R2018b 及以上（推荐 R2022a）
   - 内存：至少 8GB
   - 硬盘空间：500MB 以上

2. 安装步骤 ：
   matlab % 添加工具箱路径 addpath(genpath('ur_toolbox_path')); savepath;
   - 解压下载的 URToolbox.zip 文件；
   - 在 MATLAB 中运行上述命令将工具箱路径加入搜索路径；
   - 运行 startup_ur.m 初始化脚本。

7.1.2 配置参数与依赖库安装

URToolbox 依赖 Robotics System Toolbox（MATLAB）或 ROS（Python 版本），需安装如下依赖：

• MATLAB ：
• Robotics System Toolbox

• Simulink（用于仿真）

• Python（可选） ：
  bash pip install numpy scipy matplotlib pip install ur_toolbox

7.2 API文档与示例程序使用

7.2.1 常用API函数的说明与调用

URToolbox 提供丰富的 API 接口，以下为几个核心函数示例：

函数名	功能描述	示例用法
fkine	正向运动学计算末端位姿	T = fkine(robot, q)
ikine	逆向运动学求解关节角度	q = ikine(robot, T)
jacob0	计算雅可比矩阵	J = jacob0(robot, q)
plot	可视化机器人模型	robot.plot(q)

示例代码（正向运动学计算）：

% 创建UR5机器人模型
robot = ur5();
% 定义关节角度
q = [0, -pi/2, pi/2, 0, 0, 0];
% 计算末端位姿
T = fkine(robot, q);
disp(T);

7.2.2 示例程序的运行与调试方法

在 ur_toolbox/demo 目录下包含多个示例程序，如：

• demo_fk.m ：演示正向运动学计算
• demo_ik.m ：演示逆向运动学求解
• demo_plot.m ：可视化机器人运动

调试方法：

1. 打开 MATLAB，进入示例文件目录；
2. 使用 edit demo_fk 查看代码；
3. 插入断点逐步执行；
4. 使用 robot.plot(q) 查看当前位姿。

7.3 工具箱源码结构解析

7.3.1 核心模块的结构与功能

URToolbox 的源码结构如下：

ur_toolbox/
├── robot/               % 机器人模型定义
├── kinematics/          % 运动学相关函数
├── dynamics/            % 动力学模块
├── control/             % 控制器实现
├── utils/               % 工具函数
├── demos/               % 示例程序
└── startup_ur.m         % 初始化脚本

• robot/ ：定义 UR3、UR5、UR10 等不同型号的机器人 DH 参数；
• kinematics/ ：包含 fkine 、 ikine 等运动学函数；
• control/ ：提供 PID 控制器、轨迹跟踪算法等；
• utils/ ：常用数学工具、坐标变换函数等。

7.3.2 模块间的数据交互与调用关系

模块间通过标准接口进行数据交互，如：

• fkine 调用 robot 模型中的 DH 参数；
• ikine 依赖 fkine 实现迭代求解；
• jacob0 依赖 fkine 的结果进行雅可比矩阵计算；
• 控制模块调用 ikine 获取目标角度后进行 PID 调节。

7.4 工业应用实践案例

7.4.1 URToolbox 在装配、搬运等场景的应用

案例 1：自动装配任务

在汽车零部件装配中，URToolbox 被用于路径规划与末端姿态控制：

% 定义目标位姿
T_target = transl(0.4, 0.2, 0.3) * trotz(pi/2);
% 求解逆运动学
q_target = ikine(robot, T_target);
% 控制机器人移动至目标位置
controller.moveJ(q_target);

案例 2：物料搬运路径规划

使用 URToolbox 的 jtraj 函数生成平滑轨迹：

q0 = [0, -pi/2, pi/2, 0, 0, 0];  % 初始关节角
qf = [pi/2, -pi/2, pi/2, 0, 0, 0]; % 目标关节角
t = 0:0.01:1;
[q, qd, qdd] = jtraj(q0, qf, t);

7.4.2 工业现场中的部署与优化策略

• 部署流程 ：
  1. 在开发环境调试 URToolbox 算法；
  2. 将核心算法打包为 .mex 或 Python 模块；
  3. 部署到工业控制计算机（IPC）；
  4. 与 UR 机械臂通过 Modbus TCP 或 ROS 接口通信。

• 优化策略 ：

• 使用 codegen 将 MATLAB 函数编译为 C/C++ 提高执行效率；
• 使用 parfor 加速多解处理；
• 在 ROS 环境中使用 Gazebo 进行虚拟调试，减少现场调试时间。

7.5 使用许可与法律规范

7.5.1 开源许可协议与商业使用限制

URToolbox 基于 GNU General Public License v3.0（GPLv3） 发布，其核心特点包括：

• 允许自由使用、修改和分发；
• 修改后的代码也必须开源；
• 不提供商业用途的免责条款；
• 禁止将 URToolbox 的源码用于闭源产品。

7.5.2 合规使用与法律责任说明

在工业应用中，如需使用 URToolbox 进行商业化部署，需注意以下几点：

• 若使用其核心算法作为产品功能，建议与原作者沟通获得授权；
• 如对代码进行修改，需保留原始版权声明；
• 避免将 URToolbox 的 GPL 代码与闭源模块直接链接，建议使用接口隔离；
• 遵守当地机器人安全标准（如 ISO 10218）与数据保护法规（如 GDPR）。

本文还有配套的精品资源，点击获取

简介：UR机器人仿真工具箱是一款专为Universal Robots系列机器人设计的高级仿真平台，涵盖运动学、动力学和控制系统的理论与实现。工具箱支持路径规划、碰撞检测、动态性能分析等功能，提供前向与逆向运动学算法、PID控制器及自定义控制策略实现，适用于机器人任务规划与算法验证。压缩包中包含源码、示例程序、API文档和安装脚本，方便用户快速部署和二次开发。该工具箱在学术研究与工业应用中均具有重要价值，助力高效机器人系统开发与优化。

本文还有配套的精品资源，点击获取