基于matlab实现PCA图像压缩重建Matlab程序主成分分析图像的压缩和重建MATLAB程序。
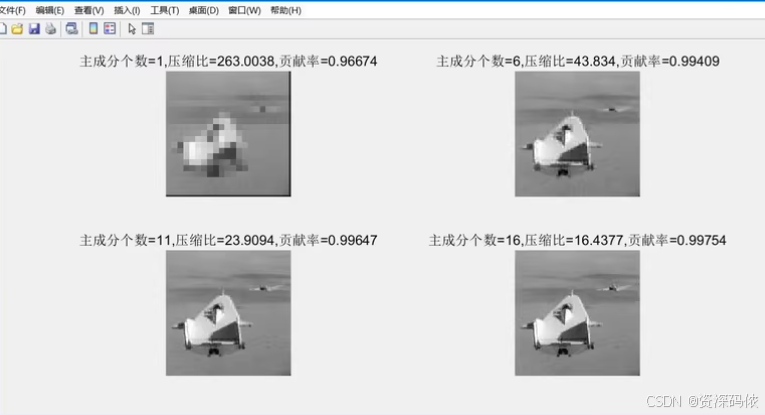
在这里插入图片描述

文章目录


主成分分析（PCA）是一种用于数据降维的统计方法，它也可以应用于图像压缩。下面是一个简单的MATLAB程序示例，演示如何使用PCA进行图像压缩和重建。

MATLAB代码实现

1. 加载并显示原始图像
% 加载图像
img = imread('your_image_file.jpg'); % 替换为你的图片文件路径
img_gray = rgb2gray(img); % 如果图像是彩色的，先转换为灰度图像

% 显示原始图像
figure;
imshow(img_gray);
title('原始图像');
2. 图像矩阵重塑

将二维图像矩阵转换为一维向量，以便于PCA处理。

% 将图像转换为列向量
[m, n] = size(img_gray);
img_vector = reshape(img_gray, m*n, 1);

% 将多个图像向量组合成一个矩阵，这里仅有一个图像
img_matrix = double(img_vector);

注意：如果处理多幅图像，则可以将每幅图像作为一个列向量添加到img_matrix中。

3. 数据标准化

在应用PCA之前，通常需要对数据进行标准化处理。

% 标准化数据
mean_img = mean(img_matrix);
std_img = std(img_matrix);
img_standardized = (img_matrix - mean_img) ./ std_img;
4. PCA变换

使用MATLAB内置函数pca来执行PCA变换。

% 执行PCA
[coeff, score, latent] = pca(img_standardized');

% 显示解释方差比例
explained_variance = cumsum(latent) / sum(latent);
figure;
plot(explained_variance, '-o');
xlabel('主成分数量');
ylabel('累计解释方差比例');
title('累计解释方差 vs 主成分数量');
5. 压缩与重建

选择一定数量的主成分来进行图像压缩和重建。

% 选择前k个主成分
k = 50; % 可以根据需要调整k值

% 使用前k个主成分重构图像
reconstructed_score = score(:, 1:k) * coeff(:, 1:k)';
reconstructed_img_standardized = reconstructed_score' * std_img + mean_img;

% 将一维向量重新转换为二维图像
reconstructed_img = uint8(reshape(reconstructed_img_standardized, m, n));

% 显示重建后的图像
figure;
imshow(reconstructed_img);
title(['使用前 ', num2str(k), ' 个主成分重建的图像']);

注意事项

  • 上述代码假设输入的是单幅灰度图像。如果要处理彩色图像或批量处理多幅图像，需要相应地调整代码。
  • 在实际应用中，你可能需要根据图像的特点和需求调整PCA参数，如选择合适的主成分数量k。
  • pca函数是MATLAB Statistics and Machine Learning Toolbox的一部分，确保你的MATLAB环境中已安装此工具箱。

通过上述步骤，你可以使用PCA技术对图像进行压缩和重建。希望这些信息对你有所帮助！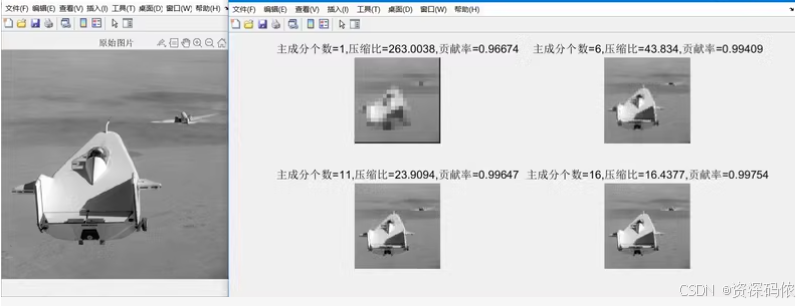
在这里插入图片描述
为了实现基于PCA的图像压缩和重建，我们可以按照以下步骤进行：

  1. 加载图像：读取原始图像。
  2. 预处理：将图像转换为灰度图像，并将其重塑为一维向量。
  3. 标准化数据：对图像数据进行标准化处理。
  4. PCA变换：使用PCA对图像数据进行降维。
  5. 压缩与重建：选择一定数量的主成分进行图像重建。
  6. 显示结果：显示原始图像和不同主成分数量下的重建图像。

以下是完整的MATLAB代码示例：

% 加载图像
img = imread('your_image_file.jpg'); % 替换为你的图片文件路径
img_gray = rgb2gray(img); % 如果图像是彩色的，先转换为灰度图像

% 显示原始图像
figure;
imshow(img_gray);
title('原始图像');

% 将图像转换为列向量
[m, n] = size(img_gray);
img_vector = reshape(img_gray, m*n, 1);

% 标准化数据
mean_img = mean(img_vector);
std_img = std(img_vector);
img_standardized = (img_vector - mean_img) ./ std_img;

% 执行PCA
[coeff, score, latent] = pca(img_standardized');

% 显示解释方差比例
explained_variance = cumsum(latent) / sum(latent);
figure;
plot(explained_variance, '-o');
xlabel('主成分数量');
ylabel('累计解释方差比例');
title('累计解释方差 vs 主成分数量');

% 不同主成分数量下的重建图像
k_values = [1, 6, 11, 16];
figure;
for i = 1:length(k_values)
    k = k_values(i);
    
    % 使用前k个主成分重构图像
    reconstructed_score = score(:, 1:k) * coeff(:, 1:k)';
    reconstructed_img_standardized = reconstructed_score' * std_img + mean_img;
    
    % 将一维向量重新转换为二维图像
    reconstructed_img = uint8(reshape(reconstructed_img_standardized, m, n));
    
    % 计算压缩比和贡献率
    compression_ratio = m*n / k;
    explained_variance_k = explained_variance(k);
    
    % 显示重建后的图像
    subplot(2, 2, i);
    imshow(reconstructed_img);
    title(['主成分数=', num2str(k), ', 压缩比=', num2str(compression_ratio), ', 贡献率=', num2str(explained_variance_k)]);
end

代码说明

  1. 加载图像：

    img = imread('your_image_file.jpg');
img_gray = rgb2gray(img);

  2. 预处理：

    [m, n] = size(img_gray);
img_vector = reshape(img_gray, m*n, 1);

  3. 标准化数据：

    mean_img = mean(img_vector);
std_img = std(img_vector);
img_standardized = (img_vector - mean_img) ./ std_img;

  4. PCA变换：

    [coeff, score, latent] = pca(img_standardized');

  5. 压缩与重建：

    k_values = [1, 6, 11, 16];
for i = 1:length(k_values)
    k = k_values(i);
    
    reconstructed_score = score(:, 1:k) * coeff(:, 1:k)';
    reconstructed_img_standardized = reconstructed_score' * std_img + mean_img;
    
    reconstructed_img = uint8(reshape(reconstructed_img_standardized, m, n));
    
    compression_ratio = m*n / k;
    explained_variance_k = explained_variance(k);
    
    subplot(2, 2, i);
    imshow(reconstructed_img);
    title(['主成分数=', num2str(k), ', 压缩比=', num2str(compression_ratio), ', 贡献率=', num2str(explained_variance_k)]);
end

  6. 显示结果：

    figure;
plot(explained_variance, '-o');
xlabel('主成分数量');
ylabel('累计解释方差比例');
title('累计解释方差 vs 主成分数量');

通过上述代码，你可以看到不同主成分数量下的图像重建效果以及对应的压缩比和贡献率。希望这些信息对你有所帮助！
在这里插入图片描述
为了实现基于PCA的图像压缩和重建，我们可以按照以下步骤进行：

  1. 加载图像：读取原始图像。
  2. 预处理：将图像转换为灰度图像，并将其重塑为一维向量。
  3. 标准化数据：对图像数据进行标准化处理。
  4. PCA变换：使用PCA对图像数据进行降维。
  5. 压缩与重建：选择一定数量的主成分进行图像重建。
  6. 显示结果：显示原始图像和不同主成分数量下的重建图像。

以下是完整的MATLAB代码示例：

% 加载图像
img = imread('your_image_file.jpg'); % 替换为你的图片文件路径
img_gray = rgb2gray(img); % 如果图像是彩色的，先转换为灰度图像

% 显示原始图像
figure;
imshow(img_gray);
title('原始图像');

% 将图像转换为列向量
[m, n] = size(img_gray);
img_vector = reshape(img_gray, m*n, 1);

% 标准化数据
mean_img = mean(img_vector);
std_img = std(img_vector);
img_standardized = (img_vector - mean_img) ./ std_img;

% 执行PCA
[coeff, score, latent] = pca(img_standardized');

% 显示解释方差比例
explained_variance = cumsum(latent) / sum(latent);
figure;
plot(explained_variance, '-o');
xlabel('主成分数量');
ylabel('累计解释方差比例');
title('累计解释方差 vs 主成分数量');

% 不同主成分数量下的重建图像
k_values = [1, 6, 11, 16];
figure;
for i = 1:length(k_values)
    k = k_values(i);
    
    % 使用前k个主成分重构图像
    reconstructed_score = score(:, 1:k) * coeff(:, 1:k)';
    reconstructed_img_standardized = reconstructed_score' * std_img + mean_img;
    
    % 将一维向量重新转换为二维图像
    reconstructed_img = uint8(reshape(reconstructed_img_standardized, m, n));
    
    % 计算压缩比和贡献率
    compression_ratio = m*n / k;
    explained_variance_k = explained_variance(k);
    
    % 显示重建后的图像
    subplot(2, 2, i);
    imshow(reconstructed_img);
    title(['主成分数=', num2str(k), ', 压缩比=', num2str(compression_ratio), ', 贡献率=', num2str(explained_variance_k)]);
end

代码说明

  1. 加载图像：

    img = imread('your_image_file.jpg');
img_gray = rgb2gray(img);

  2. 预处理：

    [m, n] = size(img_gray);
img_vector = reshape(img_gray, m*n, 1);

  3. 标准化数据：

    mean_img = mean(img_vector);
std_img = std(img_vector);
img_standardized = (img_vector - mean_img) ./ std_img;

  4. PCA变换：

    [coeff, score, latent] = pca(img_standardized');

  5. 压缩与重建：

    k_values = [1, 6, 11, 16];
for i = 1:length(k_values)
    k = k_values(i);
    
    reconstructed_score = score(:, 1:k) * coeff(:, 1:k)';
    reconstructed_img_standardized = reconstructed_score' * std_img + mean_img;
    
    reconstructed_img = uint8(reshape(reconstructed_img_standardized, m, n));
    
    compression_ratio = m*n / k;
    explained_variance_k = explained_variance(k);
    
    subplot(2, 2, i);
    imshow(reconstructed_img);
    title(['主成分数=', num2str(k), ', 压缩比=', num2str(compression_ratio), ', 贡献率=', num2str(explained_variance_k)]);
end

  6. 显示结果：

    figure;
plot(explained_variance, '-o');
xlabel('主成分数量');
ylabel('累计解释方差比例');
title('累计解释方差 vs 主成分数量');

通过上述代码，你可以看到不同主成分数量下的图像重建效果以及对应的压缩比和贡献率。希望这些信息对你有所帮助！

# matlab # 计算机视觉 # opencv
Logo
火山引擎 ADG 社区

火山引擎开发者社区是火山引擎打造的AI技术生态平台，聚焦Agent与大模型开发，提供豆包系列模型（图像/视频/视觉）、智能分析与会话工具，并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长，新用户可领50万Tokens权益，助力构建智能应用。

更多推荐

Chess用户界面设计：Tailwind CSS样式系统和组件库

GitHub推荐项目精选中的ch/chess是一个类似chess.com的多人在线象棋平台，它采用现代化的前端技术栈构建，尤其在用户界面设计上通过Tailwind CSS样式系统和组件库实现了优雅且功能丰富的交互体验。本文将深入探讨该项目如何利用Tailwind CSS打造一致的设计语言和高效的组件系统，为象棋爱好者提供沉浸式的游戏界面。## 🎨 Tailwind CSS样式系统：构建统一视

avatar 火山引擎 ADG 社区

终极指南：GPT-Engineer如何通过AI自动发现代码问题并提升质量

GPT-Engineer是一款强大的AI驱动代码工具，它能帮助开发者自动检测潜在代码问题、优化代码质量，让编程效率提升3倍以上。无论是新手还是资深开发者，都能通过这款工具轻松发现代码中的隐藏缺陷，减少调试时间，释放更多精力在创造性工作上。## 一键发现代码问题：GPT-Engineer的AI审查魔力GPT-Engineer的核心能力在于其内置的智能代码分析系统。通过集成Python代码格式

avatar 火山引擎 ADG 社区

SatDump中的纠错编码技术：从RS码到Turbo码的完整实现指南

在卫星数据传输过程中，信号往往会受到各种干扰，导致数据错误。SatDump作为一款通用卫星数据处理软件，集成了多种先进的纠错编码技术，确保从卫星接收到的数据能够准确解码。本文将深入解析SatDump中从Reed-Solomon（RS）码到Turbo码的实现细节，帮助读者理解这些技术如何保障卫星通信的可靠性。## 为什么纠错编码对卫星数据至关重要？卫星与地面站之间的通信链路面临着空间辐射、大

avatar 火山引擎 ADG 社区