自适应进化课程用于大语言模型推理
强化学习(RL)已被证明在微调大型语言模型(LLMs)方面非常有效,显著增强了它们在数学和代码生成等领域的推理能力。影响RL微调成功的一个关键因素是训练课程:即训练问题的呈现顺序。虽然随机课程作为常见的基线方法,但它们仍然次优;手动设计的课程通常依赖于启发式规则,在线过滤方法可能计算成本过高。为了解决这些限制,我们提出了自适应进化课程(SEC),这是一种自动课程学习方法,与RL微调过程同时学习课程
Xiaoyin Chen* 1,2{ }^{1,2}1,2, Jiarui Lu 1,2{ }^{1,2}1,2, Minsu Kim 1,3{ }^{1,3}1,3, Dinghuai Zhang 1,4{ }^{1,4}1,4, Jian Tang 1,5{ }^{1,5}1,5
Alexandre Piché 6{ }^{6}6, Nicolas Gontier 6{ }^{6}6, Yoshua Bengio 1,2{ }^{1,2}1,2, Ehsan Kamalloo 6{ }^{6}6
1{ }^{1}1 Mila - Quebec AI Institute, 2{ }^{2}2 Université de Montréal
3{ }^{3}3 KAIST, 4{ }^{4}4 Microsoft Research, 5{ }^{5}5 HEC Montréal, 6{ }^{6}6 ServiceNow Research
xiaoyin.chen@mila.quebec
摘要
强化学习(RL)已被证明在微调大型语言模型(LLMs)方面非常有效,显著增强了它们在数学和代码生成等领域的推理能力。影响RL微调成功的一个关键因素是训练课程:即训练问题的呈现顺序。虽然随机课程作为常见的基线方法,但它们仍然次优;手动设计的课程通常依赖于启发式规则,在线过滤方法可能计算成本过高。为了解决这些限制,我们提出了自适应进化课程(SEC),这是一种自动课程学习方法,与RL微调过程同时学习课程策略。我们的方法将课程选择公式化为一个非平稳多臂老虎机问题,将每个问题类别(如难度级别或问题类型)视为单独的手臂。我们利用策略梯度方法中的绝对优势作为即时学习收益的代理指标。在每个训练步骤中,课程策略选择类别以最大化这一奖励信号,并使用TD(0)\operatorname{TD}(0)TD(0)方法进行更新。在三个不同的推理领域:规划、归纳推理和数学中,我们的实验表明,SEC显著提高了模型的推理能力,使其更好地泛化到更难的、分布外测试问题上。此外,当同时在多个推理领域进行微调时,我们的方法实现了更好的技能平衡。这些发现凸显了SEC作为LLMs RL微调的一种有前途的策略。
1 引言
强化学习(RL)已成为微调大型语言模型(LLMs)的核心技术[28, 35, 12],显著提升了其推理能力。最近的研究展示了显著的成功,特别是在验证生成正确性较为简单的领域[27],如数学和代码生成。通过仅由可验证结果定义的奖励来优化LLMs,RL微调鼓励复杂推理行为的出现,包括自我修正和回溯策略[25, 62, 16],从而大幅提高推理性能。
影响RL微调效果的关键因素是训练课程[7],即训练数据的呈现顺序。由于在线RL本质上依赖于策略模型本身来生成高质量的训练轨迹,因此使课程与模型当前的学习进度保持一致至关重要。理想情况下,这种一致性使模型能够持续遇到产生最大学习成果的问题[42, 29, 20]。为了具体说明这一点,我们使用Countdown游戏进行了一项对照实验,故意采用了一个次优(逆序)课程,其中问题从难到易排列。如图1所示,由此产生的模型在测试集上的表现较差,并且对更具挑战性的分布外(OOD)问题几乎没有泛化能力。相比之下,当使用基准随机课程进行训练时,其中不同难度的问题被均匀随机抽取,模型表现出显著改善的泛化能力和整体任务性能。
尽管随机课程作为一个合理的基线,它自然引发了以下问题:我们能否设计更有效的课程策略?课程学习[7]正是针对这一挑战,通过优化训练任务的排序,从而增强学习效率和效果。最近的RL微调课程学习方法通常涉及预先设计的手动课程[50, 47, 57]或基于在线样本的动态在线过滤[63, 3]。然而,手动设计的课程严重依赖于启发式规则,需要人为干预以适应新模型或任务;相反,在线过滤方法由于持续生成额外的在线样本而带来巨大的计算开销。
在本文中,我们提出了自适应进化课程(SEC)(图2),一种适用于LLMs RL微调的自动课程学习[39]方法。我们的方法在RL微调过程中自适应地学习课程策略,将课程选择公式化为一个非平稳多臂老虎机(MAB)问题[51, 49, 31]。每个课程类别(如难度级别或问题类型)被视为单独的手臂,课程策略旨在选择最大化学习成果的手臂。具体来说,我们通过梯度范数操作化学习成果的概念,注意到在策略梯度方法中,梯度范数由优势函数的绝对值加权。基于这一观察,我们将绝对优势定义为每个手臂的奖励。在每个RL训练步骤中,根据当前的MAB策略采样课程,随后使用通过当前训练步骤获得的奖励通过TD(0)\operatorname{TD}(0)TD(0)方法实时更新该策略[48]。
我们的实验表明,SEC显著提高了模型在三个不同领域的推理能力:规划、归纳推理和数学,尤其是在应对具有挑战性的分布外问题时。与标准随机课程相比,SEC实现了显著的相对改进,例如在Countdown上达到13%,在Zebra谜题上达到21%,在ARC-1D上达到22%,以及在AIME24数据集上高达33%。当同时在多个推理领域进行微调时,SEC有效地平衡了跨任务的表现,强调了其作为LLMs RL微调的自动课程学习策略的力量。
2 方法
在RL微调的背景下,每个训练步骤ttt,课程策略从训练问题集DDD中选择子集Dt⊆DD_{t} \subseteq DDt⊆D提供给LLM。在我们的工作中,我们考虑这样的情景:训练问题可以分为NNN个不同的类别。这个假设简化了课程优化问题,即将类别ccc映射到实数值分数的学习预期回报Qt(c)Q_{t}(c)Qt(c)(第2.1节)。然后通过首先根据课程策略采样类别,再在类别内均匀采样问题来构建训练批次。
课程策略的目标是最大化LLM的最终任务性能。然而,直接评估这种性能需要完成整个RL微调过程,而课程策略最好能随着训练步骤一起更新。为了解决这个问题,我们引入了一个局部可测量的奖励作为引导课程策略的代理目标(第2.2节)。
2.1 课程选择作为多臂老虎机
用于推理任务的训练数据集通常可以自然地分解为不同的类别。例如,如果数据集涵盖各种推理领域,如数学、编码和规划,这些领域自然形成不同的类别。当数据集在任务类型或领域上同质时,仍可以通过基于域内的级别(如难度)对示例进行分类来构建课程。例如,MATH数据集[17]根据Art of Problem Solving (AoPS)提供的指南将问题分为五个不同的难度级别。此外,在没有明确难度注释的情况下,问题难度可以通过训练LLM的经验准确性或在额外预处理步骤中提示专家LLM来估计,正如Shi等人[46]所展示的那样。
受这些考虑的启发,我们假设,特别是对于专注于推理的数据集,训练问题可以划分为NNN个不同的类别C={c1,c2,…,cN}C=\left\{c_{1}, c_{2}, \ldots, c_{N}\right\}C={c1,c2,…,cN}。概念上,课程策略优化问题可以视为部分可观测马尔可夫决策过程(POMDP):状态对应当前LLM策略,动作对应课程选择,奖励由可观测的性能指标定义,如与所选课程相关的在线性能。
此POMDP公式与非平稳多臂老虎机(MAB)问题极为相似,每个臂代表一个问题类别cic_{i}ci,目标是学习在训练步骤ttt选择类别ccc的预期回报Qt(c)Q_{t}(c)Qt(c)。重要的是,这里的MAB是非平稳的:每个臂的预期奖励分布随着训练过程中LLM策略的更新而变化。为了解决这个已深入研究的非平稳老虎机问题[51, 49],我们利用经典的TD(0)\operatorname{TD}(0)TD(0)方法[48]迭代更新Qt(c)Q_{t}(c)Qt(c):
Qt+1(c)=αrt(c)+(1−α)Qt(c) Q_{t+1}(c)=\alpha r_{t}(c)+(1-\alpha) Q_{t}(c) Qt+1(c)=αrt(c)+(1−α)Qt(c)
其中α\alphaα是学习率,Q0(c)=0Q_{0}(c)=0Q0(c)=0初始化分数为零,rt(c)r_{t}(c)rt(c)表示下一节定义的奖励。注意这还被称为指数移动平均。课程策略可以简单地定义在Qt(c)Q_{t}(c)Qt(c)之上,详见第2.3节。
2.2 使用绝对优势衡量学习成果
理想的课程应最大化LLM在整个训练周期后在测试数据上的最终性能。然而,直接测量这一目标需要完成完整的RL微调循环。尽管评估中间检查点可以在一定程度上缓解这一问题,频繁
评估计算代价高昂。为克服这一挑战,我们引入了一个代理目标,该目标可以在每次训练步骤中高效计算。
此类代理目标的一个直观选择是优先考虑最大化模型即时学习成果的训练数据 [42, 29, 20],即那些导致参数大幅更新的数据。实际上,这可以通过测量损失函数相对于选定训练数据的梯度范数来量化。具体来说,考虑一个策略梯度算法,该算法通过最小化以下损失函数来优化LLM策略:
LPG(θ)=−E(st,at)∼πθ[logπθ(at∣st)A^t] \mathcal{L}_{\mathrm{PG}}(\theta)=-\mathbb{E}_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta}}\left[\log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \widehat{A}_{t}\right] LPG(θ)=−E(st,at)∼πθ[logπθ(at∣st)A t]
其中πθ\pi_{\theta}πθ表示LLM策略,A^t\widehat{A}_{t}A t表示优势值。那么每步(st,at)(s_{t}, a_{t})(st,at)的梯度范数为:
∥∇θLPG(θ,st,at)∥2=∥E(st,at)∼πθ[∇θlogπθ(at∣st)A^t]∥2≈∣A^t∣∥∇θlogπθ(at∣st)∥2 \left\|\nabla_{\theta} \mathcal{L}_{\mathrm{PG}}\left(\theta, s_{t}, a_{t}\right)\right\|_{2}=\left\|\mathbb{E}_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \widehat{A}_{t}\right]\right\|_{2} \approx\left|\widehat{A}_{t}\right|\left\|\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right)\right\|_{2} ∥∇θLPG(θ,st,at)∥2= E(st,at)∼πθ[∇θlogπθ(at∣st)A t] 2≈ A t ∥∇θlogπθ(at∣st)∥2
我们观察到梯度大小由优势的绝对值∣A^t∣\left|\widehat{A}_{t}\right| A t 加权。因此,我们通过批量期望∣A^t∣\left|\widehat{A}_{t}\right| A t 近似课程ccc的学习增益:
r(c)=E(st,at)∼πθ(xi),xi∼c∣A^t∣ r(c)=\mathbb{E}_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta}\left(x_{i}\right), x_{i} \sim c}\left|\widehat{A}_{t}\right| r(c)=E(st,at)∼πθ(xi),xi∼c A t
换句话说,课程ccc在每次训练步骤中的奖励计算为与课程类别ccc相关问题的所有rollout的平均绝对优势。
在具有可验证奖励的RL中解释绝对优势。最近关于推理任务的RL微调工作经常采用二进制正确性奖励(错误为0,正确为1)与Group Relative Policy Optimization(GRPO)算法[44, 25, 12, 30, 56],这被称为具有可验证奖励的RL[27]。在这里,我们展示了在这种常见设置下,方程3形式化的预期绝对优势在二进制奖励为0.5时最大化。这意味着当问题对当前模型既不太容易也不太困难时,学习增益最高。优先训练这类难度的问题自然符合教育心理学中的概念,特别是最近发展区理论[54, 8],并将我们的方法与更广泛的课程学习文献联系起来[14, 15, 52, 3]。
具体而言,GRPO算法通过从相同问题中采样nnn个rollout来估计优势。第iii个rollout的优势计算为:A^t,i=r~i=ri− mean (r)std(r)\widehat{A}_{t, i}=\tilde{r}_{i}=\frac{r_{i}-\text { mean }(r)}{\operatorname{std}(r)}A
t,i=r~i=std(r)ri− mean (r),其中rir_{i}ri是第iii个rollout的二进制奖励,mean (r)(r)(r)和std(r)\operatorname{std}(r)std(r)分别表示所有nnn个rollout的奖励均值和标准差。由于奖励是二进制的,它可以建模为伯努利分布;因此,mean (r)=p(r)=p(r)=p和std(r)=p(1−p)\operatorname{std}(r)=\sqrt{p(1-p)}std(r)=p(1−p),其中ppp表示成功率。预期绝对优势可以表示为:
E[∣A^t,i∣]=E[∣r~i∣]=E[∣ri−pp(1−p)∣] \mathbb{E}\left[\left|\widehat{A}_{t, i}\right|\right]=\mathbb{E}\left[\left|\tilde{r}_{i}\right|\right]=\mathbb{E}\left[\left|\frac{r_{i}-p}{\sqrt{p(1-p)}}\right|\right] E[ A t,i ]=E[∣r~i∣]=E[ p(1−p)ri−p ]
因为rir_{i}ri是伯努利分布,只有两个可能的值:
r~i={1−pp(1−p) with probability p−pp(1−p) with probability 1−p \tilde{r}_{i}= \begin{cases}\frac{1-p}{\sqrt{p(1-p)}} & \text { with probability } p \\ \frac{-p}{\sqrt{p(1-p)}} & \text { with probability } 1-p\end{cases} r~i=⎩ ⎨ ⎧p(1−p)1−pp(1−p)−p with probability p with probability 1−p
因此,问题的预期绝对优势为
E[∣r~i∣]=p1−pp(1−p)+(1−p)pp(1−p)=2p(1−p)p(1−p)=2p(1−p) \mathbb{E}\left[\left|\tilde{r}_{i}\right|\right]=p \frac{1-p}{\sqrt{p(1-p)}}+(1-p) \frac{p}{\sqrt{p(1-p)}}=\frac{2 p(1-p)}{\sqrt{p(1-p)}}=2 \sqrt{p(1-p)} E[∣r~i∣]=pp(1−p)1−p+(1−p)p(1−p)p=p(1−p)2p(1−p)=2p(1−p)
我们可以看到函数g(p)=2p(1−p)g(p)=2 \sqrt{p(1-p)}g(p)=2p(1−p)在p=0.5p=0.5p=0.5处对称,并在区间[0,1][0,1][0,1]上严格凹,最大值出现在p=0.5p=0.5p=0.5。这一推导表明,最大化预期绝对优势等价于优先选择成功率为0.5的问题。
算法 1 SEC: 自适应进化课程的RL微调
输入:训练集 DDD 分成类别 C={c1,…,cN}C=\left\{c_{1}, \ldots, c_{N}\right\}C={c1,…,cN}; LLM 策略 πθ\pi_{\theta}πθ 参数 θ\thetaθ; 学习率 α\alphaα (用于 QQQ 更新); 温度 τ\tauτ; 批量大小 BBB; 总训练步骤 TTT;
奖励函数 R;\mathcal{R} ;R; RL 算法 A\mathcal{A}A
初始化 Q0(c)←0∀c∈CQ_{0}(c) \leftarrow 0 \forall c \in CQ0(c)←0∀c∈C
对于 t←0t \leftarrow 0t←0 到 T−1T-1T−1:
Bt←∅B_{t} \leftarrow \emptysetBt←∅
当 ∣Bt∣<B\left|B_{t}\right|<B∣Bt∣<B:
采样类别 c∼Softmax(Qt(c)/τ)c \sim \operatorname{Softmax}\left(Q_{t}(c) / \tau\right)c∼Softmax(Qt(c)/τ)
从类别 ccc 中均匀采样问题 xxx
Bt←Bt∪{x}B_{t} \leftarrow B_{t} \cup\{x\}Bt←Bt∪{x}
结束 while
在每个 x∈Btx \in B_{t}x∈Bt 上运行 πθ\pi_{\theta}πθ 生成 rollout T\mathcal{T}T 并用 R\mathcal{R}R 计算奖励 r\mathbf{r}r
估计优势 A~\widetilde{A}A
并用 A(πθ,T,r)\mathcal{A}\left(\pi_{\theta}, \mathcal{T}, \mathbf{r}\right)A(πθ,T,r) 更新 πθ\pi_{\theta}πθ
对于所有 c∈Cc \in Cc∈C:
Bc←{x∈Bt∣xB_{c} \leftarrow\left\{x \in B_{t} \mid x\right.Bc←{x∈Bt∣x 属于类别 c}\left.c\right\}c}
rt(c)←1∣Bc∣∑j:xj∈Bc1Tj∑tTj∣A~t,j∣r_{t}(c) \leftarrow \frac{1}{\left|B_{c}\right|} \sum_{j: x_{j} \in B_{c}} \frac{1}{T_{j}} \sum_{t}^{T_{j}}\left|\widetilde{A}_{t, j}\right|rt(c)←∣Bc∣1∑j:xj∈BcTj1∑tTj
A
t,j
Qt+1(c)←αrt(c)+(1−α)Qt(c)Q_{t+1}(c) \leftarrow \alpha r_{t}(c)+(1-\alpha) Q_{t}(c)Qt+1(c)←αrt(c)+(1−α)Qt(c)
结束 for
结束 for
返回 微调后的 LLM πθ\pi_{\theta}πθ
备注:上述推导旨在提供在常见RL微调设置下我们提出的客观分析,以及对其一般行为的直观见解。然而,这并不意味着我们的方法局限于这种特定场景。实际上,我们的实验经验证明,即使应用非二进制奖励函数(第3.2节)和替代RL算法(第3.4节),SEC也能实现强大的性能。
2.3 自适应进化课程用于RL微调
在每个RL训练步骤中,按如下方式生成一批问题。首先,根据当前Qt(c)Q_{t}(c)Qt(c)值定义的玻尔兹曼分布采样子类别:p(c)=cQt(c)/τ∑i=1Ne(βi/τi)/τp(c)=\frac{c^{Q_{t}(c) / \tau}}{\sum_{i=1}^{N} \mathrm{e}^{\left(\beta_{i} / \tau_{i}\right) / \tau}}p(c)=∑i=1Ne(βi/τi)/τcQt(c)/τ,其中τ\tauτ是控制探索-利用权衡的温度参数。接下来,从选定的类别中均匀采样问题。此过程重复进行,直到达到所需的批大小。从玻尔兹曼分布中采样自然在课程选择中平衡探索和利用。
然后使用生成的批次更新LLM策略。在每次步骤更新策略后,我们计算每个采样子类别ccc的奖励r(c)r(c)r(c),并使用方程1更新相应的Qt(c)Q_{t}(c)Qt(c)值。SEC的完整过程总结在算法1中。
3 实验
本节介绍在三个推理领域(规划、归纳推理和数学)中评估SEC的实验。我们还调查了SEC在不同课程类别和替代RL算法下的有效性。
3.1 实验设置
我们在开放权重Qwen2.5模型[61]上进行实验:Qwen2.5-3B和Qwen2.57B。对于推理任务的RL微调,我们使用广泛使用的GRPO算法[44, 12]。我们报告从最佳检查点计算的平均pass@1准确率,每个问题生成8次独立结果。附录B提供了更多的训练和评估细节。所有任务的提示和数据示例见附录C。
表1:跨推理任务和课程方法的评估。准确率通过每个问题的8次独立生成的pass@1平均值计算。分布内(ID)结果是在与训练相同的三个难度级别中抽样的测试问题上平均得出的。每个数据集和模型大小的最佳课程策略以粗体显示,第二佳的以下划线显示。SEC在任务中始终表现出色,特别在具有挑战性的OOD测试问题上提高了泛化能力。
| 任务 | 分割 | Qwen2.5 3B | Qwen2.5 7B | ||||
|---|---|---|---|---|---|---|---|
| 随机 | 有序 | SEC(我们的) | 随机 | 有序 | SEC(我们的) | ||
| Countdown | ID | 0.859 | 0.551 | 0.866 | 0.858 | 0.820 | 0.872 |
| OOD | 0.479 | 0.321 | 0.542 | 0.566 | 0.442 | 0.555 | |
| Zebra | ID | 0.517 | 0.534 | 0.547 | 0.573 | 0.572 | 0.587 |
| OOD | 0.285 | 0.329 | 0.345 | 0.321 | 0.311 | 0.355 | |
| ARC-1D | ID | 0.501 | 0.476 | 0.500 | 0.512 | 0.526 | 0.514 |
| OOD | 0.313 | 0.363 | 0.381 | 0.436 | 0.428 | 0.418 | |
| Math | MATH500 | 0.668 | 0.672 | 0.672 | 0.774 | 0.759 | 0.761 |
| AMC22-23 | 0.345 | 0.352 | 0.351 | 0.486 | 0.477 | 0.511 | |
| AIME24 | 0.075 | 0.054 | 0.100 | 0.138 | 0.150 | 0.175 |
我们的实验涵盖了三种需要不同能力的推理领域:(i)规划,需要前瞻搜索和回溯;(ii)归纳推理,涉及从观察中学习一般规则并将其应用于未见过的情景;和(iii)数学,需要多步逻辑演绎和系统性问题解决。
规划。对于规划任务,我们考虑两个流行的谜题问题:(i)倒计时,目标是使用基本算术运算从给定的一组3-6个整数中得到目标数字。在这个谜题中,我们通过增加给定的整数数量来控制任务难度。(ii)斑马谜题,这是一个经典的逻辑谜题,涉及3-6个实体(如房屋)每个具有3-6个属性(如颜色)。给定一组文本线索(约束条件),目标是正确分配每个属性到每个实体。在这里,我们通过增加实体和属性的数量来控制任务难度。
归纳推理。我们采用抽象和推理语料库(ARC)的1D变体[9, 60]进行归纳推理。每个谜题实例由长度为10、20、30或40的字符串组成(长度越大,难度越高),这些字符串定义在整数上。提供了三个输入-输出示例,说明潜在规则,LLM在未见过的情况下进行测试。
对于上述三个推理任务(倒计时、斑马和ARC),我们使用Open-Thought框架[34]生成问题。具体来说,我们的训练数据包含三个最简单的难度级别,最难的级别保留为分布外(OOD)评估集。对于每个难度级别,我们采样10,000个问题用于训练和200个保留样本用于评估。在RL微调期间,我们对正确的问题给予1分奖励,对答案不正确但格式正确的给予0.1分奖励,否则得分为0。
数学。我们在MATH数据集[17]的训练分割上训练LLMs,该数据集包含按五个难度级别分类的问题,从1(最简单)到5(最难),如数据集注释中指定。与前三个任务不同,数学任务的训练数据在这些难度级别之间不平衡(图S1)。对于此任务,我们使用二元奖励(正确得1分,否则得0分),不对正确格式赋予部分奖励。随后在MATH500、AMC22-23和AIME24数据集上评估模型。
3.2 主要结果
首先,我们使用问题难度作为课程类别评估SEC的有效性,即每个难度级别对应于MAB框架中的一个臂。我们将SEC与两种常用的课程策略进行比较:(1)随机/无课程,其中训练样本按照原始数据分布均匀地从所有难度级别中抽取,这对应于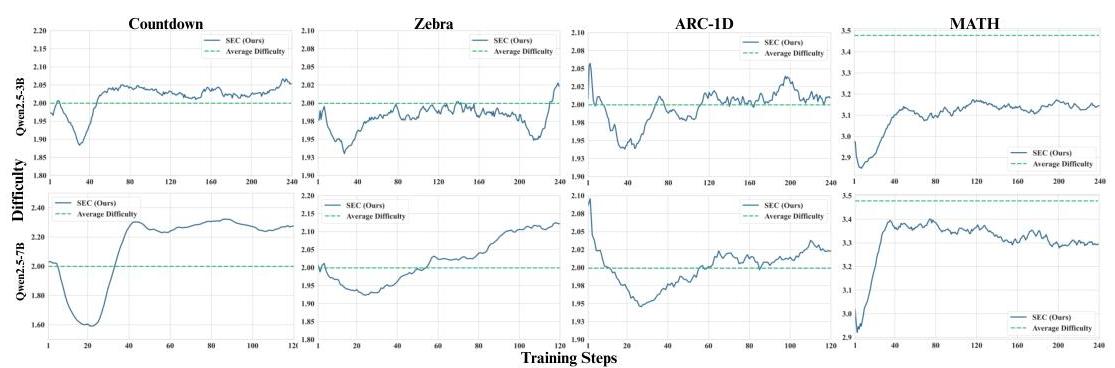
图3:随训练步骤的平均样本难度。SEC在RL微调过程中自适应调整任务难度。蓝色曲线表示采样难度,使用移动平均平滑,绿色虚线表示数据集的平均难度。在所有基准(列)和模型大小(顶部:Qwen2.5-3B,底部,Qwen2.5-7B)中,SEC最初选择较容易的问题,并随着训练的进行逐步引入更具挑战性的问题,有效地将难度与模型改进对齐。
传统的“无课程”方法,和(2)难度递增课程,其中问题从最容易到最难依次呈现。SEC在所有实验设置中的超参数详细信息见附录B。
我们的结果,汇总在表1中,显示了SEC在任务和模型上的明显优势。对于较小的Qwen2.5-3B模型,SEC在更难的、分布外(OOD)测试集上始终实现显著改进。具体来说,在倒计时任务中,与随机基线相比,SEC显著提高了OOD准确率约13%(从0.48到0.54),与难度递增基线相比提高了约69%(从0.32到0.54)。类似地,在斑马任务中,SEC相对于随机基线实现了约21%的相对改进(从0.29到0.35)。在数学领域,与随机基线相比,SEC在具有挑战性的AIME数据集上显著提高了约33%的性能(从0.075到0.10)。
对于较大的Qwen2.5-7B模型,SEC的性能具有竞争力,但在像倒计时和ARC这样的任务上与随机课程更为相似。这一结果符合预期,因为更强的基础模型可能已经具备足够的推理能力来应对更难的问题,从而使显式的课程指导变得不那么关键。然而,在更具挑战性的斑马和数学任务中,SEC继续显示出明显的改进。具体来说,斑马任务的OOD准确率相对于随机基线提高了约11%(从0.32到0.36)。在具有挑战性的AIME问题上,SEC实现了27%的相对增益(从0.14到0.18)。在这些更具挑战性的领域中观察到的一致改进,以及在3B模型中的稳健增益,突显了SEC在提高模型泛化能力方面的有效性。
最后,难度递增课程往往产生次优性能,可能是由于其固定的难度安排不能动态适应模型的当前表现。结果,模型可能在容易的问题上花费过多的训练时间,限制了从可能更有助于学习的更难问题中的暴露。这些结果进一步强调了像SEC这样的自适应、在线课程策略的必要性,这种策略可以持续将问题选择与模型的当前学习状态对齐。
课程分析。图3展示了SEC如何在不同任务和模型中自适应调整训练难度。对于每个任务和模型,采样的难度(蓝色曲线)最初低于或接近数据集的平均难度(绿色虚线),表明SEC最初强调较容易的问题以促进早期阶段的学习。随着训练的进行,SEC逐渐增加所选问题的难度,使训练复杂性与模型不断提高的能力相匹配。值得注意的是,SEC为更强的Qwen2.5-7B模型选择的问题比小的3B模型更难,进一步证实了SEC有效适应其课程以匹配模型学习能力的能力。这种跨任务和模型的自适应模式突显了SEC在动态调整问题难度以最大化学习成果方面的优势。
| 任务 | 分割 | 随机 | SEC-2D |
|---|---|---|---|
| 倒计时 | ID | 0.837 | 0.839\mathbf{0 . 8 3 9}0.839 |
| OOD | 0.418 | 0.428\mathbf{0 . 4 2 8}0.428 | |
| 斑马 | ID | 0.513 | 0.539\mathbf{0 . 5 3 9}0.539 |
| OOD | 0.254 | 0.312\mathbf{0 . 3 1 2}0.312 | |
| ARC | ID | 0.380 | 0.418\mathbf{0 . 4 1 8}0.418 |
| OOD | 0.251 | 0.327\mathbf{0 . 3 2 7}0.327 |
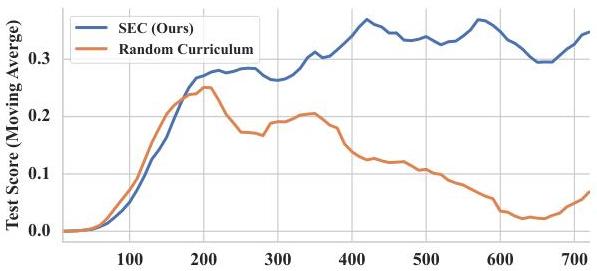
图4:在多个任务上训练时的性能比较。左:Qwen2.5-3B在ID和OOD分割上的测试准确率。SEC-2D通过为每种问题类型和难度级别的组合定义一个臂来实现。SEC-2D在所有任务上始终实现更高的准确率,显示了相对于随机课程在多任务上的改进泛化能力。右:倒计时OOD准确率与训练步骤的关系,通过移动平均平滑。随机课程的性能在训练中途崩溃,突出其无法有效平衡多个任务。相比之下,SEC-2D在整个训练过程中保持稳定性能。
3.3 SEC与多种课程类别
在本节中,我们演示了SEC可以无缝支持同时从多个和多样化的课程类别中抽取。RL微调的常见情景涉及优化模型在多个推理领域的表现。为了评估SEC在这种多任务设置中的表现,我们将倒计时、斑马和ARC的训练数据集结合起来,创建一个包含多种推理问题的混合训练集,并使用Qwen2.5-3B模型进行RL微调。目标是实现所有推理任务的整体强表现。
我们的基于MAB的课程框架对课程类别的语义含义不敏感,从而允许类别任意定义。在此实验中,我们为每种问题类型的唯一组合和3个难度级别定义一个臂,共得到9个不同的臂。我们将这种变体称为SEC-2D。
图4展示了在多个推理任务上同时训练时SEC-2D的评估结果。表格(左)表明SEC-2D在所有三个推理任务中始终优于随机课程。学习曲线(右)提供了倒计时任务随训练进展的OOD准确率的详细视图。起初,两种课程都显示出快速提升;然而,随机课程在训练中期表现出显著的性能崩溃,突出了其无法有效平衡多任务学习。相比之下,SEC-2D在整个训练过程中保持稳定、稳健的性能,突显了其在自适应平衡多个学习目标方面的优势。
3.4 SEC与替代RL算法
虽然我们的主要实验使用了GRPO算法,我们还评估了SEC与其他广泛使用的RL方法,特别是近端策略优化(PPO)[43]和REINFORCE Leave-One-Out(RLOO)[24]。表2展示了在Qwen2.5-3B上的倒计时任务结果,比较了SEC与随机课程在这两种算法下的表现。在PPO和RLOO中,SEC在ID和OOD评估分割上始终提升性能,表明其在单一RL算法之外也有效。
表2:SEC在倒计时任务上使用替代RL算法。SEC在不同RL算法(PPO、RLOO)下改进了RL微调性能,与随机课程相比。
| RL 方法 | 分割 | 随机 | SEC |
|---|---|---|---|
| PPO | ID | 0.621 | 0.750\mathbf{0 . 7 5 0}0.750 |
| OOD | 0.159 | 0.224\mathbf{0 . 2 2 4}0.224 | |
| RLOO | ID | 0.821 | 0.859\mathbf{0 . 8 5 9}0.859 |
| OOD | 0.465 | 0.494\mathbf{0 . 4 9 4}0.494 |
4 相关工作
RL微调语言模型。语言模型(LMs)可以自然地被视为顺序决策制定策略,生成基于部分文本状态的标记直到达到终端输出。通常,奖励信号是稀疏和周期性的,仅在完整生成后分配,这种方法称为结果奖励模型(ORM)[11]。一些最近的研究引入了过程奖励模型(PRM),在生成过程中分配中间奖励以促进
局部信用分配 [28, 53]。利用这种马尔可夫决策过程(MDP)框架,RL微调已在多个领域取得了成功,包括使LM与人类偏好对齐(RLHF)[10, 65, 4, 36]、通过精确匹配奖励增强数学推理能力 [44] 和通过内部LM分布进行自训练(例如,自教推理器,STaR)[64]。最近,带有可验证奖励的强化学习(RLVR)[12, 27] 已成为提高LM推理能力的有前景范式。
为这些MDP公式定制的RL方法也发挥了核心作用。策略梯度方法,包括REINFORCE变体(例如,RLOO)[58, 24, 1] 和近端策略优化(PPO)方法 [43, 21, 44],因其相对稳定性而被广泛采用。另一种方法是离线和基于价值的算法,如定向偏好优化(DPO)[41, 32] 和生成流网络(GFlowNets)[6, 19, 18],在样本效率、多样性和异步训练方面具有优势 [33, 5],尽管它们可能不总是匹配在线方法的任务特定奖励最大化能力,而是优先考虑提高多样性。
课程学习。课程学习由Bengio等人引入[7],后来发展为自步学习[26],显示组织示例从易到难可以平滑非凸优化并提高泛化能力。在RL中,课程减轻了稀疏奖励和探索障碍:反向课程生成从目标向外扩展起始状态[14],教师-学生课程学习(TSCL)[31] 还使用非平稳多臂老虎机框架来最大化测量的学习进展,定义为任务性能的改进,方法如POET、ACCEL和PAIRED共同演化任务与智能体[55, 38, 13],Kim等人[22] 提出了一种自适应教师,动态调整多模态摊销采样的课程。
最近,类似的课程学习思想开始影响语言模型的RL微调。R3\mathrm{R}^{3}R3 特别适用于链式思维推理,逐步揭示更长的推理序列,基于黄金演示[59]。Qi等人[40] 提出了WEBRL,一种自进化在线课程RL框架,旨在通过提示另一个LLM自主生成基于先前失败的新任务来训练基于LM的网络代理。
与此同时,两项值得注意的研究探讨了RL微调的自动课程学习:Bae等人[3] 提出了通过反复生成解决方案来估计其难度的在线训练问题过滤方法,带来了大量的计算开销;AdaRFT[46] 根据模型最近的奖励信号自适应调整课程难度,但依赖于明确的难度级别排序,限制了其在其他课程类别中的通用性。
与这些方法不同,我们的SEC方法利用一般的非平稳多臂老虎机公式动态调整课程,使其广泛适用于各种课程类别、任意奖励尺度和各种RL算法。
5 结论
在本文中,我们介绍了自适应进化课程(SEC),这是专为LLMs的RL微调设计的自动课程学习框架。SEC将自适应课程选择公式化为一个非平稳多臂老虎机问题,根据模型不断发展的能力动态调整问题难度。在包括规划、归纳推理和数学在内的各种推理任务的广泛实验表明,SEC始终改善泛化能力,并有效平衡在多个推理领域的同时学习。
我们的框架包括三个主要组成部分:课程奖励、采样方法和更新规则。在本文中,SEC采用绝对优势作为课程奖励,玻尔兹曼分布进行采样,并采用TD(0)更新方法。这些组件的推广可以作为未来工作的方向。例如,可以通过利用上界置信度(UCB)[2] 或汤普森采样[51] 等方法将不确定性度量纳入课程选择。
局限性。虽然SEC在各种推理任务中表现出一贯的有效性,但它也有一些局限性。目前我们的方法依赖于预定义的课程类别;其在自动推断或不太明确定义的类别中的有效性尚未探索。此外,SEC引入了额外的超参数(如温度、学习率),需要调整。未来的工作可以探索更灵活的课程定义,例如基于嵌入聚类问题或使用轻量级模型(如线性回归)直接估计课程奖励。
我们要感谢Dzmitry Bahdanau和Nicolas Chapados的深刻见解和对本项目的帮助。作者感谢CIFAR、NSERC和未来生命研究所的资助。Minsu Kim得到了KAIST Jang Yeong Sil奖学金的支持。
参考文献
[1] Arash Ahmadian, Chris Cremer, Matthias Gallé, Marzieh Fadaee, Julia Kreutzer, Olivier Pietquin, Ahmet Üstün, 和 Sara Hooker. 回到基础:重新审视通过人类反馈学习的强化优化方法在大型语言模型中的应用。arXiv预印本 arXiv:2402.14740, 2024.
[2] Peter Auer. 使用置信界限进行利用-探索权衡。机器学习研究杂志,3(Nov):397-422, 2002.
[3] Sanghwan Bae, Jiwoo Hong, Min Young Lee, Hanbyul Kim, JeongYeon Nam, 和 Donghyun Kwak. 面向推理导向强化学习的在线难度过滤。arXiv预印本 arXiv: 2504.03380, 2025.
[4] Yuntao Bai, Andy Jones, Kamal Ndousse, Amanda Askell, Anna Chen, Nova DasSarma, Dawn Drain, Stanislav Fort, Deep Ganguli, Tom Henighan, Nicholas Joseph, Saurav Kadavath, Jackson Kernion, Tom Conerly, Sheer El-Showk, Nelson Elhage, Zac Hatfield-Dodds, Danny Hernandez, Tristan Hume, Scott Johnston, Shauna Kravec, Liane Lovitt, Neel Nanda, Catherine Olsson, Dario Amodei, Tom Brown, Jack Clark, Sam McCandlish, Chris Olah, Ben Mann, 和 Jared Kaplan. 通过人类反馈的强化学习训练一个有用且无害的助手。arXiv预印本 arXiv: 2204.05862, 2022.
[5] Brian R Bartoldson, Siddarth Venkatraman, James Diffenderfer, Moksh Jain, Tal Ben-Nun, Seanie Lee, Minsu Kim, Johan Obando-Ceron, Yoshua Bengio, 和 Bhavya Kailkhura. 异步轨迹平衡:解耦探索与学习以快速、可扩展地对LLM进行后训练。arXiv预印本 arXiv:2503.18929, 2025.
[6] Emmanuel Bengio, Moksh Jain, Maksym Korablyov, Doina Precup, 和 Yoshua Bengio. 基于流网络的生成模型用于非迭代多样候选生成。神经信息处理系统进展,34:27381-27394, 2021.
[7] Yoshua Bengio, Jérôme Louradour, Ronan Collobert, 和 Jason Weston. 课程学习。第26届国际机器学习会议论文集,ICML '09,页41-48,纽约,NY,美国,2009。计算机协会。ISBN 9781605585161。doi: 10.1145/1553374.1553380。URL https://doi.org/10.1145/ 1553374 . 1553380 .
[8] Seth Chaiklin 等人。Vygotsky学习与教学分析中的最近发展区。Vygotsky的文化情境教育理论,1(2):39-64, 2003.
[9] François Chollet. 智力测量的研究。arXiv预印本 arXiv:1911.01547, 2019.
[10] Paul Christiano, Jan Leike, Tom B. Brown, Miljan Martic, Shane Legg, 和 Dario Amodei. 基于人类偏好的深度强化学习。arXiv预印本 arXiv: 1706.03741, 2017.
[11] Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, 等人。训练验证器解决数学文字问题。arXiv预印本 arXiv:2110.14168, 2021.
[12] DeepSeek-AI. Deepseek-r1: 通过强化学习激励LLMs的推理能力,2025. URL https://arxiv.org/abs/2501.12948.
[13] Michael Dennis, Natasha Jaques, Eugene Vinitsky, Alexandre Bayen, Stuart Russell, Andrew Critch, 和 Sergey Levine. 无监督环境设计中出现的复杂性和零样本迁移。H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, 和 H. Lin 编辑,神经信息处理系统进展,卷33,页13049-13061。Curran Associates, Inc., 2020. URL https://proceedings.neurips.cc/paper_files/paper/ 2020/file/985e9a46e10005356bbaf194249f6856-Paper.pdf.
[14] Carlos Florensa, David Held, Markus Wulfmeier, Michael Zhang, 和 Pieter Abbeel. 强化学习的反向课程生成。机器人学习会议,页482-495。PMLR, 2017.
[15] Carlos Florensa, David Held, Xinyang Geng, 和 Pieter Abbeel. 强化学习代理的自动目标生成。机器学习国际会议,页1515−15281515-15281515−1528. PMLR, 2018.
[16] Kanishk Gandhi, Ayush Chakravarthy, Anikait Singh, Nathan Lile, 和 Noah D. Goodman. 启发自我改进推理者的认知行为,或者,高度有效的星星的四个习惯。arXiv预印本 arXiv: 2503.01307, 2025.
[17] Dan Hendrycks, Collin Burns, Saurav Kadavath, Akul Arora, Steven Basart, Eric Tang, D. Song, 和 J. Steinhardt. 使用数学数据集衡量数学问题解决能力。NeurIPS 数据集和基准测试,2021.
[18] Matthew Ho, Vincent Zhu, Xiaoyin Chen, Moksh Jain, Nikolay Malkin, 和 Edwin Zhang. Proof Flow: 正式推理生成流网络语言模型调整的初步研究。arXiv预印本 arXiv: 2410.13224, 2024.
[19] Edward J Hu, Moksh Jain, Eric Elmoznino, Younesse Kaddar, Guillaume Lajoie, Yoshua Bengio, 和 Nikolay Malkin. 大型语言模型中的难处理推断摊销。国际学习表示会议 (ICLR), 2024.
[20] Angelos Katharopoulos 和 François Fleuret. 并非所有样本都是平等创造的:使用重要性采样的深度学习。机器学习国际会议,页2525-2534。PMLR, 2018.
[21] Amirhossein Kazemnejad, Milad Aghajohari, Eva Portelance, Alessandro Sordoni, Siva Reddy, Aaron Courville, 和 Nicolas Le Roux. Vineppo: 解锁用于LLM推理的RL潜力通过精炼信用分配。arXiv预印本 arXiv:2410.01679, 2024.
[22] Minsu Kim, Sanghyeok Choi, Taeyoung Yun, Emmanuel Bengio, Leo Feng, Jarrid Rector-Brooks, Sungsoo Ahn, Jinkyoo Park, Nikolay Malkin, 和 Yoshua Bengio. 自适应教师用于摊销采样器。国际学习表示会议 (ICLR), 2025.
[23] Diederik P Kingma 和 Jimmy Ba. Adam: 一种随机优化方法。arXiv预印本 arXiv:1412.6980, 2014.
[24] Wouter Kool, Herke van Hoof, 和 Max Welling. 买4个REINFORCE样本,免费获得一个基线! 在ICLR结构预测深度强化学习研讨会,2019.
[25] Aviral Kumar, Vincent Zhuang, Rishabh Agarwal, Yi Su, John D Co-Reyes, Avi Singh, Kate Baumli, Shariq Iqbal, Colton Bishop, Rebecca Roelofs, Lei M Zhang, Kay McKinney, Disha Shrivastava, Cosmin Paduraru, George Tucker, Doina Precup, Feryal Behbahani, 和 Aleksandra Faust. 通过强化学习训练语言模型以自我修正。arXiv预印本 arXiv: 2409.12917, 2024.
[26] M. Pawan Kumar, Benjamin Packer, 和 Daphne Koller. 潜变量模型的自步学习。神经信息处理系统进展(NeurIPS),页1189-1197,2010.
[27] Nathan Lambert, Jacob Morrison, Valentina Pyatkin, Shengyi Huang, Hamish Ivison, Faeze Brahman, Lester James V. Miranda, Alisa Liu, Nouha Dziri, Shane Lyu, Yuling Gu, Saumya Malik, Victoria Graf, Jena D. Hwang, Jiangjiang Yang, Ronan Le Bras, Oyvind Tafjord, Chris Wilhelm, Luca Soldaini, Noah A. Smith, Yizhong Wang, Pradeep Dasigi, 和 Hannaneh Hajishirzi. Tulu 3: 推动开放语言模型后训练的前沿。arXiv预印本 arXiv: 2411.15124, 2024.
[28] Hunter Lightman, Vineet Kosaraju, Yuri Burda, Harrison Edwards, Bowen Baker, Teddy Lee, Jan Leike, John Schulman, Ilya Sutskever, 和 Karl Cobbe. 让我们逐步验证。第十二届国际学习表示会议,2023.
[29] Ilya Loshchilov 和 Frank Hutter. 在线批量选择以加速神经网络训练。arXiv预印本 arXiv:1511.06343, 2015.
[30] Michael Luo, Sijun Tan, Roy Huang, Xiaoxiang Shi, Rachel Xin, Colin Cai, Ameen Patel, Alpay Ariyak, Qingyang Wu, Ce Zhang, Li Erran Li, Raluca Ada Popa, 和 Ion Stoica. Deepcoder: 全开源14B编码器在O3-mini级别。https://pretty-radio-b75.notion.site/ DeepCoder-A-Fully-Open-Source-14B-Coder-at-03-mini-Level-1cf81902c14680b3bee5eb349a512a51, 2025. Notion博客。
[31] Tambet Matiisen, Avital Oliver, Taco Cohen, 和 John Schulman. 教师-学生课程学习。IEEE神经网络与学习系统汇刊,31(9):3732-3740, 2020. doi: 10.1109/TNNLS.2020.2983146.
[32] Yu Meng, Mengzhou Xia, 和 Danqi Chen. Simpo: 使用参考自由奖励的简单偏好优化。神经信息处理系统进展,37:124198-124235, 2024.
[33] Michael Noukhovitch, Shengyi Huang, Sophie Xhonneux, Arian Hosseini, Rishabh Agarwal, 和 Aaron Courville. 异步RLHF: 更快更高效的离线策略RL用于语言模型。arXiv预印本 arXiv:2410.18252, 2024.
[34] Open-Thought. 推理健身房。https://github.com/open-thought/reasoning-gym/, 2025.
[35] OpenAI. 学习用LLMs推理。https://openai.com/index/ learning-to-reason-with-11ms/. 访问日期:2025-03-21.
[36] Long Ouyang, Jeffrey Wu, Xu Jiang, Diogo Almeida, Carroll Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, 等人。通过人类反馈训练语言模型遵循指令。神经信息处理系统进展,35:27730-27744, 2022.
[37] Jiayi Pan, Junjie Zhang, Xingyao Wang, Lifan Yuan, Hao Peng, 和 Alane Suhr. Tinyzero. https://github.com/Jiayi-Pan/TinyZero, 2025. 访问日期:2025-01-24.
[38] Jack Parker-Holder, Minqi Jiang, Michael Dennis, Mikayel Samvelyan, Jakob Foerster, Edward Grefenstette, 和 Tim Rocktäschel. 使用基于后悔的环境设计演化课程。第39届国际机器学习会议(ICML)论文集,2022.
[39] Rémy Portelas, Cédric Colas, Lilian Weng, Katja Hofmann, 和 Pierre-Yves Oudeyer. 深度RL的自动课程学习:简短综述。国际人工智能联合会议,2020. doi: 10.24963/ijcai.2020/671.
[40] Zehan Qi, Xiao Liu, Iat Long Iong, Hanyu Lai, Xueqiao Sun, Wenyi Zhao, Yu Yang, Xinyue Yang, Jiadai Sun, Shuntian Yao, 等人。WebRL: 通过自进化在线课程强化学习训练LLM Web代理。arXiv预印本 arXiv:2411.02337, 2024.
[41] Rafael Rafailov, Archit Sharma, Eric Mitchell, Christopher D Manning, Stefano Ermon, 和 Chelsea Finn. 直接偏好优化:你的语言模型实际上是一个奖励模型。神经信息处理系统进展,36:53728-53741, 2023.
[42] Tom Schaul, John Quan, Ioannis Antonoglou, 和 David Silver. 优先经验回放。arXiv预印本 arXiv:1511.05952, 2015.
[43] John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, 和 Oleg Klimov. 近端策略优化算法。arXiv预印本 arXiv:1707.06347, 2017.
[44] Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Xiao Bi, Haowei Zhang, Mingchuan Zhang, Y. K. Li, Y. Wu, 和 Daya Guo. DeepseekMath: 推动开放语言模型中数学推理的极限。arXiv预印本 arXiv: 2402.03300, 2024.
[45] Guangming Sheng, Chi Zhang, Zilingfeng Ye, Xibin Wu, Wang Zhang, Ru Zhang, Yanghua Peng, Haibin Lin, 和 Chuan Wu. Hybridflow: 一个灵活高效的RLHF框架。arXiv预印本 arXiv:2409.19256, 2024.
[46] Taiwei Shi, Yiyang Wu, Linxin Song, Tianyi Zhou, 和 Jieyu Zhao. 高效强化微调通过自适应课程学习。arXiv预印本 arXiv: 2504.05520, 2025.
[47] Mingyang Song, Mao Zheng, Zheng Li, Wenjie Yang, Xuan Luo, Yue Pan, 和 Feng Zhang. FastCurl: 通过渐进上下文扩展实现高效训练R1类推理模型的课程强化学习。arXiv预印本 arXiv: 2503.17287, 2025.
[48] Richard S. Sutton. 通过时间差分法学习预测。机器学习,3(1):9-44, 1988年8月。ISSN 0885-6125. doi: 10.1023/A:1022633531479. URL https: //doi.org/10.1023/A:1022633531479.
[49] Richard S. Sutton 和 Andrew G. Barto. 强化学习:导论。Bradford Book, Cambridge, MA, USA, 2018. ISBN 0262039249.
[50] Kimi团队, Angang Du, Bofei Gao, Bowei Xing, Changjiu Jiang, Cheng Chen, Cheng Li, Chenjun Xiao, Chenzhuang Du, Chonghua Liao, 等人。Kimi K1.5: 使用LLMs扩展强化学习。arXiv预印本 arXiv:2501.12599, 2025.
[51] William R Thompson. 根据两个样本的证据判断一个未知概率是否超过另一个的概率。Biometrika, 25(3/4):285-294, 1933.
[52] Georgios Tzannetos, Bárbara Gomes Ribeiro, Parameswaran Kamalaruban, 和 Adish Singla. 强化学习智能体的近端课程。arXiv预印本 arXiv:2304.12877, 2023.
[53] Jonathan Uesato, Nate Kushman, Ramana Kumar, Francis Song, Noah Siegel, Lisa Wang, Antonia Creswell, Geoffrey Irving, 和 Irina Higgins. 使用过程和结果反馈解决数学文字问题。arXiv预印本 arXiv: 2211.14275, 2022.
[54] Lev Semenovich Vygotsky 和 Michael Cole. 社会中的思维:高级心理过程的发展。哈佛大学出版社,1978.
[55] Rui Wang, Joel Lehman, Jeff Clune, 和 Kenneth O. Stanley. POET(配对开放式先驱者):无尽生成越来越复杂和多样化的学习环境及其解决方案。遗传与进化计算会议(GECCO '19)论文集,页142-151。ACM, 2019.
[56] Yuxiang Wei, Olivier Duchenne, Jade Copet, Quentin Carbonneaux, Lingming Zhang, Daniel Fried, Gabriel Synnaeve, Rishabh Singh, 和 Sida I. Wang. Swe-RL: 通过开放软件演化的强化学习提升LLM推理。arXiv预印本 arXiv: 2502.18449, 2025.
[57] Liang Wen, Yunke Cai, Fenrui Xiao, Xin He, Qi An, Zhenyu Duan, Yimin Du, Junchen Liu, Lifu Tang, Xiaowei Lv, 等人。Light-R1: 从头开始和超越的长链思考课程SFT、DPO和RL。arXiv预印本 arXiv:2503.10460, 2025.
[58] Ronald J Williams. 连接主义强化学习的简单统计梯度跟随算法。机器学习,8:229-256, 1992.
[59] Zhiheng Xi, Wenxiang Chen, Boyang Hong, Senjie Jin, Rui Zheng, Wei He, Yiwen Ding, Shichun Liu, Xin Guo, Junzhe Wang, 等人。通过逆向课程强化学习训练大型语言模型进行推理。arXiv预印本 arXiv:2402.05808, 2024.
[60] Yudong Xu, Wenhao Li, Pashootan Vaezipoor, Scott Sanner, 和 Elias B Khalil. LLMs和抽象与推理语料库:成功、失败及基于对象表示的重要性。arXiv预印本 arXiv:2305.18354, 2023.
[61] An Yang, Baosong Yang, Beichen Zhang, Binyuan Hui, Bo Zheng, Bowen Yu, Chengyuan Li, Dayiheng Liu, Fei Huang, Haoran Wei, 等人。Qwen2.5技术报告。arXiv预印本 arXiv:2412.15115, 2024.
[62] Edward Yeo, Yuxuan Tong, Morry Niu, Graham Neubig, 和 Xiang Yue. 揭示大语言模型中长链思考推理的奥秘。arXiv预印本 arXiv: 2502.03373, 2025.
[63] Qiying Yu, Zheng Zhang, Ruofei Zhu, Yufeng Yuan, Xiaochen Zuo, Yu Yue, Tiantian Fan, Gaohong Liu, Lingjun Liu, Xin Liu, 等人。Dapo: 一个大规模开源的大语言模型强化学习系统。arXiv预印本 arXiv:2503.14476, 2025.
[64] Eric Zelikman, Yuhuai Wu, Jesse Mu, 和 Noah Goodman. STAR: 通过推理引导推理。神经信息处理系统进展,35:15476-15488, 2022.
[65] Daniel M. Ziegler, Nisan Stiennon, Jeffrey Wu, Tom B. Brown, Alec Radford, Dario Amodei, Paul Christiano, 和 Geoffrey Irving. 通过人类偏好微调语言模型。arXiv预印本 arXiv: 1909.08593, 2019.
A 社会影响声明
本文介绍了SEC,这是一种旨在通过强化学习增强语言模型推理能力的课程学习方法。通过提高模型准确性和泛化能力,SEC可能带来积极的社会影响,例如更可靠的AI助手和教育环境中更好的可访问性。然而,正如任何增强语言模型的方法一样,存在潜在的负面影响:更强的推理能力可能会促进虚假信息或欺骗性内容生成等滥用行为。因此,必须结合负责任的AI实践,包括强大的监控和缓解策略,来管理和最小化可能的有害影响。
B 实现细节
训练。所有模型都使用Volcano Engine Reinforcement Learning(verl)库[45]中实现的GRPO算法[44]进行微调。我们分别训练了Qwen2.5 [61]的3B和7B参数变体。对于每个三个谜题任务,Qwen2.5-3B的微调过程总共持续240个梯度步骤,Qwen2.5-7B则为120个步骤,每个批次大小为256。优势通过8次rollout进行估计。两个模型都在数学任务上训练了240个步骤。我们通过将相应的损失权重设置为0来不应用Kullback-Leibler(KL)散度损失。我们在整个研究中将最大提示长度限制为1,024个token,最大响应长度限制为4,096个token。模型参数使用Adam[23]进行优化,学习率为1e-6,beta为(0.9,0.99)(0.9,0.99)(0.9,0.99),没有warm-up步骤。所有的训练实验都在4-8个NVIDIA H100 80GB GPU上进行。表S1总结了每个实验中使用的SEC超参数。
| 模型 | 倒计时 | 斑马 | ARC | 数学 |
|---|---|---|---|---|
| Qwen2.5 3B | α=0.5,τ=1.0\alpha=0.5, \tau=1.0α=0.5,τ=1.0 | α=0.5,τ=1.0\alpha=0.5, \tau=1.0α=0.5,τ=1.0 | α=0.5,τ=1.0\alpha=0.5, \tau=1.0α=0.5,τ=1.0 | α=0.2,τ=1.0\alpha=0.2, \tau=1.0α=0.2,τ=1.0 |
| Qwen2.5 7B | α=0.5,τ=0.2\alpha=0.5, \tau=0.2α=0.5,τ=0.2 | α=0.5,τ=0.4\alpha=0.5, \tau=0.4α=0.5,τ=0.4 | α=0.5,τ=1.0\alpha=0.5, \tau=1.0α=0.5,τ=1.0 | α=0.5,τ=0.4\alpha=0.5, \tau=0.4α=0.5,τ=0.4 |
表S1:每个实验中使用的超参数设置(学习率α\alphaα和温度τ\tauτ)。
在第3.3节的多任务实验中,我们在混合数据集上对Qwen2.5-3B模型进行3×240=7203 \times 240=7203×240=720步的微调。我们使用α=0.5\alpha=0.5α=0.5和τ=0.2\tau=0.2τ=0.2。
在第3.4节中,我们在所有实验中对Qwen2.5-3B进行120步的训练。对于RLOO,我们同样使用8次rollout进行优势估计,并为SEC使用α=0.5,τ=0.25\alpha=0.5, \tau=0.25α=0.5,τ=0.25。对于PPO,我们为SEC使用α=0.5,τ=1\alpha=0.5, \tau=1α=0.5,τ=1,并为GAE参数使用λ=1,γ=1\lambda=1, \gamma=1λ=1,γ=1。与我们的主要实验一致,我们不应用KL散度损失。
模型。以下是我们在实验中使用的模型:
-
Qwen2.5-3B: https://huggingface.co/Qwen/Qwen2.5-3B
-
- Qwen2.5-7B: https://huggingface.co/Qwen/Qwen2.5-7B
数学数据集。以下是我们在实验中使用的数据来源:
- Qwen2.5-7B: https://huggingface.co/Qwen/Qwen2.5-7B
-
MATH500: https://huggingface.co/datasets/HuggingFaceH4/MATH-500
-
- AMC22-23: https://huggingface.co/datasets/AI-MO/aimo-validation-amc
-
- AIME: https://huggingface.co/datasets/Maxwell-Jia/AIME_2024
C 数据示例
以下是我们在研究中为每个任务列出的提示和数据示例。提示模板采用自Pan等人[37]。
倒计时提示:
用户和助手之间的对话。用户提问,助手回答。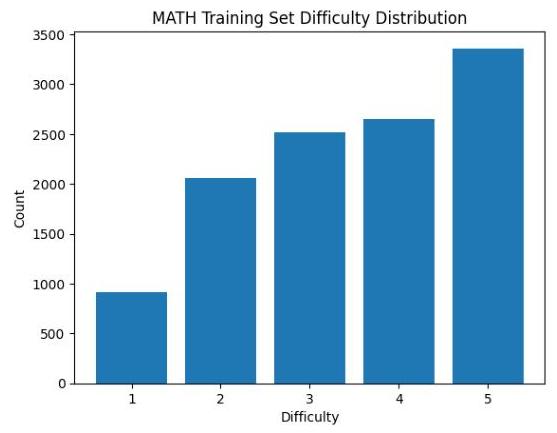
图S1:MATH训练集中难度级别的分布。
用户:使用数字[5, 17, 91]创建一个等于113的方程式。只能使用基本算术运算(=,−,∗,/=,-, *, /=,−,∗,/),并且每个数字必须恰好使用一次。将最终答案放在\boxed{}中,例如\\backslash\ boxed {(1+\{(1+{(1+ 2) / 3}。助手:让我一步步解决这个问题。
斑马谜题提示:
用户和助手之间的对话。用户提问,助手回答。助手首先在心中考虑推理过程,然后向用户提供答案。
用户:这是一个逻辑谜题。有3栋房子(从左到右编号为1到3),从街对面看过去,每栋房子里住着不同的人。他们有不同的特征:
- 每个人都有唯一的名字:arnold, bob, alice
-
- 每个人都有不同的雪茄喜好:dunhill, prince, pall mall
-
- 每个人养不同的动物:猫, 狗, 鸟
- 养鸟的人直接住在dunhill吸烟者的左边。
-
- Alice是狗的主人。
-
- Arnold住在第二栋房子里。
-
- Alice抽prince牌雪茄。
-
- Arnold喜欢养猫。
住在第一栋房子里的人叫什么名字?只提供人的名字作为最终答案,并将其放在\boxed{}中,例如:\boxed(Alice)。助手:让我一步步解决这个问题。
- Arnold喜欢养猫。
ARC-1D提示:
用户和助手之间的对话。用户提问,助手回答。助手首先在心中考虑推理过程,然后向用户提供答案。
用户:根据以下示例,找出将输入网格映射到输出网格的共同规则。
示例1:
输入:1212100120\begin{array}{llllllllll}1 & 2 & 1 & 2 & 1 & 0 & 0 & 1 & 2 & 0\end{array}1212100120
输出:0001111222\begin{array}{llllllllll}0 & 0 & 0 & 1 & 1 & 1 & 1 & 2 & 2 & 2\end{array}0001111222
示例2:
输入:1 2 0 0 0 0 0 2 0 1 2
输出:0 0 0 0 0 0 1 1 2 2 2
示例3:
输入:0 0 2 0 0 0 0 0 1 1 1 0
输出:0 0 0 0 0 0 0 0 1 1 1 2
下面是测试输入网格。通过应用你找到的规则预测对应的输出网格。详细描述你是如何得出规则以及整体推理过程的,在提交答案之前。你的最终答案必须放在\boxed{}中,仅应为测试输出网格本身。
输入:0 0 2 0 0 1 1 1 0 0 1 助手:让我一步步解决这个问题。
数学提示:
用户和助手之间的对话。用户提问,助手回答。助手首先在心中考虑推理过程,然后向用户提供答案。
用户:求出
338182+338192+338202+338212+338222 33818^{2}+33819^{2}+33820^{2}+33821^{2}+33822^{2} 338182+338192+338202+338212+338222
除以17的余数。将你的最终答案放在\boxed{}内。助手:让我一步步解决这个问题。
参考论文:https://arxiv.org/pdf/2505.14970

火山引擎开发者社区是火山引擎打造的AI技术生态平台,聚焦Agent与大模型开发,提供豆包系列模型(图像/视频/视觉)、智能分析与会话工具,并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长,新用户可领50万Tokens权益,助力构建智能应用。
更多推荐
 已为社区贡献287条内容
已为社区贡献287条内容






所有评论(0)