理解核心公式

w = w - \eta \frac{\partial L(w,b)}{\partial w}

b = b - \eta \frac{\partial L(w,b)}{\partial b}

这两条公式是梯度下降的核心。我们可以把它拆解成几个部分来理解：

  1. w 和b: 这是我们想要优化的模型参数 (权重和偏置)。

  2. \frac{\partial L}{\partial w} 和\frac{\partial L}{\partial b}: 这是偏导数, 代表你当前位置的 "坡度"。

  3. \eta (学习率): 这是学习率(Learning Rate)。它决定了我们每走一步要迈多大的步子。

  4. 减号(-): 这个减号非常关键。它确保了我们总是朝着坡度下降的方向走。

为什么是减号？

  1. 偏导数指示方向：

    • 正的坡度（\frac{\partial L}{\partial w}>0）：这表示如果你增加 w，损失函数 L 也会增加。也就是你在往上坡走。

    • 负的坡度（\frac{\partial L}{\partial w}<0）：这表示如果你增加 w，损失函数 L会减少。也就是你在往下坡走。

  2. 减号确保下坡：

    • 如果当前坡度是正的（\frac{\partial L}{\partial w}>0），为了下山，你需要减小 w的值。

    • 公式是：w_{\text{new}}=w_{\text{old}}​−(正数)。这里的减号就保证了 w_{\text{new}} 比 w_{\text{old}} 小，实现了下坡。

    • 如果当前坡度是负的（\frac{\partial L}{\partial w}<0），为了下山，你需要增加 w 的值。

    • 公式是：w_{\text{new}}=w_{\text{old}}−(负数)。负负得正，这也就等同于 w_{\text{old}}​+(正数)，保证了 w_{\text{new}} 比w_{\text{old}}​ 大，同样实现了下坡。

        总而言之，无论偏导数是正还是负，这个减号都能确保我们沿着损失函数值减小的方向（下坡）移动。这就是为什么它如此重要，因为我们的目标就是不断减小损失，直到达到最小值。

把它想象成“下山”

我们把这整个过程想象成一个下山的过程。

  • 你站在山上某个位置，想走到山谷的最低点。

  • 坡度（偏导数）告诉你，往哪个方向走是下坡。

  • 学习率（\eta）决定了你每一步走多远。

  • 更新公式就是你的行动指南：“新的位置 = 当前位置 - 迈出的步子”。

举个例子：

假设你当前在山上的位置，w和b。

  1. 你先算出你所在位置的坡度（\frac{\partial L}{\partial w}和 \frac{\partial L}{\partial b}​）。

  2. 坡度告诉你，要往下走，需要改变参数 w和b。

  3. 学习率 \eta决定了你这次要走多远。

  4. 然后，你用当前的位置减去要走的距离，得到新的位置。

        这个过程会重复多次，直到你到达山谷的最低点（损失函数达到最小值），这时你的坡度会接近0，你走的步子也会越来越小，最终停下来。

为什么学习率 (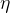\eta) 很重要？

学习率是一个非常重要的参数，它直接影响了梯度下降的效果。

  • 如果学习率太高：你每次走的步子太大，可能会跳过最低点，甚至离最低点越来越远。就像你下山时，步子太大，直接从山谷上跳过去了，反而到了另一座更高的山峰上。

  • 如果学习率太低：你每次走的步子太小，需要很长时间才能到达最低点，训练过程会非常慢。

所以，选择一个合适的学习率是成功训练模型的关键。

        总而言之，在梯度下降中，我们通过计算当前位置的坡度，并乘以学习率来确定前进的方向和大小，然后迭代地更新模型的参数，直到找到最佳解。

# 机器学习 # 人工智能
Logo
火山引擎 ADG 社区

火山引擎开发者社区是火山引擎打造的AI技术生态平台，聚焦Agent与大模型开发，提供豆包系列模型（图像/视频/视觉）、智能分析与会话工具，并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长，新用户可领50万Tokens权益，助力构建智能应用。

更多推荐

Chess用户界面设计：Tailwind CSS样式系统和组件库

GitHub推荐项目精选中的ch/chess是一个类似chess.com的多人在线象棋平台，它采用现代化的前端技术栈构建，尤其在用户界面设计上通过Tailwind CSS样式系统和组件库实现了优雅且功能丰富的交互体验。本文将深入探讨该项目如何利用Tailwind CSS打造一致的设计语言和高效的组件系统，为象棋爱好者提供沉浸式的游戏界面。## 🎨 Tailwind CSS样式系统：构建统一视

avatar 火山引擎 ADG 社区

终极指南：GPT-Engineer如何通过AI自动发现代码问题并提升质量

GPT-Engineer是一款强大的AI驱动代码工具，它能帮助开发者自动检测潜在代码问题、优化代码质量，让编程效率提升3倍以上。无论是新手还是资深开发者，都能通过这款工具轻松发现代码中的隐藏缺陷，减少调试时间，释放更多精力在创造性工作上。## 一键发现代码问题：GPT-Engineer的AI审查魔力GPT-Engineer的核心能力在于其内置的智能代码分析系统。通过集成Python代码格式

avatar 火山引擎 ADG 社区

SatDump中的纠错编码技术：从RS码到Turbo码的完整实现指南

在卫星数据传输过程中，信号往往会受到各种干扰，导致数据错误。SatDump作为一款通用卫星数据处理软件，集成了多种先进的纠错编码技术，确保从卫星接收到的数据能够准确解码。本文将深入解析SatDump中从Reed-Solomon（RS）码到Turbo码的实现细节，帮助读者理解这些技术如何保障卫星通信的可靠性。## 为什么纠错编码对卫星数据至关重要？卫星与地面站之间的通信链路面临着空间辐射、大

avatar 火山引擎 ADG 社区