目录

1. 引言

2. 单源最短路径问题的定义

3. Dijkstra 算法

3.1 算法思想

3.2 具体步骤

3.3 代码实现（以 Python 为例）

3.4 时间复杂度分析

4. Bellman - Ford 算法

4.1 算法思想

4.2 具体步骤

4.3 代码实现（以 Python 为例）

4.4 时间复杂度分析

5. SPFA 算法

5.1 算法思想

5.2 具体步骤

5.3 代码实现（以 Python 为例）

5.4 时间复杂度分析

6. 算法比较与选择

6.1 适用场景

6.2 时间复杂度

6.3 空间复杂度

7. 总结

---

1. 引言

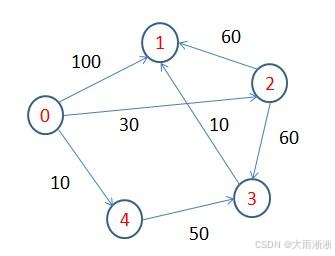
在现实生活中，我们常常会遇到需要寻找最短路径的问题。比如，当我们使用地图导航软件规划从家到公司的路线时，软件会自动为我们计算出一条用时最短或距离最短的路径；在物流运输中，物流公司需要规划出从仓库到各个配送点的最优路线，以降低运输成本和时间。这些实际应用场景都涉及到一个重要的计算机科学问题 —— 单源最短路径问题。

单源最短路径问题，简单来说，就是在一个加权图中，给定一个源节点，找到从该源节点到图中其他所有节点的最短路径。这个问题在学术研究领域同样具有重要的地位，它是图论中的经典问题之一，许多其他复杂的算法和问题都建立在其基础之上 。接下来，我们将深入探讨解决单源最短路径问题的主要算法。

2. 单源最短路径问题的定义

在图论中，图 \( G = (V, E) \) 由顶点集合 \( V \) 和边集合 \( E \) 组成。单源最短路径问题，就是在这样的一个加权图中，给定一个源顶点 \( s \in V \) ，找到从源顶点 \( s \) 到图中其他所有顶点 \( v \in V - \{s\} \) 的最短路径 。这里的路径长度是指路径上所有边的权值之和。

例如，假设有一个城市交通图，图中的顶点代表城市，边代表城市之间的道路，边的权值可以表示道路的长度或者车辆行驶所需的时间。如果我们要从城市 \( A \) 出发，前往其他各个城市，单源最短路径问题就是要找出从城市 \( A \) 到其他每个城市的最短行驶距离或最短行驶时间的路线。

更具体地，对于图 \( G \) 中的一条路径 \( P = (v_1, v_2, ..., v_k) \) ，其中 \( v_i \in V \) 且 \( (v_i, v_{i + 1}) \in E \) ，路径 \( P \) 的长度定义为 \( \sum_{i = 1}^{k - 1} w(v_i, v_{i + 1}) \) ，这里 \( w(v_i, v_{i + 1}) \) 表示边 \( (v_i, v_{i + 1}) \) 的权值。单源最短路径问题的目标就是对于给定的源顶点 \( s \) ，找到对于每个顶点 \( t \in V - \{s\} \) ，使得从 \( s \) 到 \( t \) 的路径长度最小的路径。

3. Dijkstra 算法

3.1 算法思想

Dijkstra 算法由荷兰计算机科学家艾兹赫尔・戴克斯特拉（Edsger Wybe Dijkstra）于 1956 年提出 ，是一种用于求解带权有向图中，从一个给定源点到其他所有顶点的最短路径的经典算法。该算法基于贪心思想，按路径长度递增次序生成最短路径。

Dijkstra 算法的核心在于将图中的顶点集合分为两个部分：已确定最短路径的顶点集合 \( S \) 和未确定最短路径的顶点集合 \( T \) 。初始时， \( S \) 中仅包含源点， \( T \) 包含除源点外的其他所有顶点。在每一步迭代中，从 \( T \) 中选择距离源点最近的顶点 \( u \) ，将其加入到 \( S \) 中，然后利用 \( u \) 更新 \( T \) 中其他顶点到源点的距离。通过不断重复这个过程，直到 \( T \) 为空，此时 \( S \) 中包含了所有顶点，并且每个顶点到源点的距离就是最短路径长度。

3.2 具体步骤

1. 初始化：

• • 设定源点 \( s \) 。

• • 初始化距离数组 \( dist \) ， \( dist[i] \) 表示从源点 \( s \) 到顶点 \( i \) 的当前最短距离，初始时 \( dist[s]=0 \) ，对于其他顶点 \( i \) ， \( dist[i]=\infty \) 。

• • 初始化路径数组 \( path \) ， \( path[i] \) 用于记录从源点 \( s \) 到顶点 \( i \) 的最短路径上 \( i \) 的前驱顶点，初始时 \( path[i]= - 1 \) 。

• • 初始化集合 \( S=\{s\} \) ，集合 \( T = V - \{s\} \) ，其中 \( V \) 是图中所有顶点的集合。

1. 选择最短路径：

• • 从集合 \( T \) 中选择距离源点 \( s \) 最近的顶点 \( u \) ，即 \( dist[u]=\min\{dist[v]|v\in T\} \) 。

• • 将顶点 \( u \) 从集合 \( T \) 中移除，并加入到集合 \( S \) 中。

1. 更新最短路径：

• • 对于顶点 \( u \) 的每一个邻接顶点 \( v \) ，如果 \( v\in T \) 且通过顶点 \( u \) 到达顶点 \( v \) 的距离比当前 \( dist[v] \) 更短，即 \( dist[u]+w(u, v)\lt dist[v] \) （其中 \( w(u, v) \) 表示边 \( (u, v) \) 的权值），则更新 \( dist[v] \) 和 \( path[v] \) ：

• • • \( dist[v]=dist[u]+w(u, v) \) 。

• • • \( path[v]=u \) 。

1. 重复：

• • 重复步骤 2 和步骤 3，直到集合 \( T \) 为空，此时 \( dist \) 数组中存储的就是从源点 \( s \) 到其他所有顶点的最短路径长度，通过 \( path \) 数组可以回溯得到具体的最短路径。

3.3 代码实现（以 Python 为例）

import heapq

def dijkstra(graph, start):

# 初始化距离字典，设为无穷大

distances = {vertex: float('infinity') for vertex in graph}

distances[start] = 0 # 起始节点距离为0

# 优先队列，存放节点及其距离

priority_queue = [(0, start)]

while priority_queue: # 当队列不为空

current_distance, current_vertex = heapq.heappop(priority_queue)

# 如果当前距离大于已知距离，跳过

if current_distance > distances[current_vertex]:

continue

# 遍历邻居

for neighbor, weight in graph[current_vertex].items():

distance = current_distance + weight

# 更新距离

if distance < distances[neighbor]:

distances[neighbor] = distance

heapq.heappush(priority_queue, (distance, neighbor))

return distances

# 示例图，使用邻接表表示

graph = {

'A': {'B': 1, 'C': 4},

'B': {'A': 1, 'C': 2, 'D': 5},

'C': {'A': 4, 'B': 2, 'D': 1},

'D': {'B': 5, 'C': 1}

}

# 计算从节点'A'开始的最短路径

shortest_paths = dijkstra(graph, 'A')

print(shortest_paths)

代码解释：

1. 首先创建一个 distances 字典，用于存储每个顶点到源点的距离，初始时除源点外，其他顶点的距离都设为无穷大。

1. 使用 Python 的 heapq 模块创建一个优先队列 priority_queue ，它是一个最小堆，每次从队列中取出的是距离源点最近的顶点。

1. 在循环中，不断从优先队列中取出距离最小的顶点，检查其邻居顶点。如果通过当前顶点到达邻居顶点的距离更短，则更新邻居顶点的距离，并将其加入优先队列。

1. 最后返回 distances 字典，其中包含了从源点到各个顶点的最短距离。

3.4 时间复杂度分析

• 使用邻接矩阵实现：

• • 在每次迭代中，选择距离源点最近的顶点需要遍历所有未访问的顶点，时间复杂度为 \( O(V) \) ，其中 \( V \) 是图中顶点的数量。

• • 总共需要进行 \( V - 1 \) 次迭代，每次迭代还需要更新邻居顶点的距离，这部分操作对于每个顶点也需要 \( O(V) \) 的时间（因为要遍历邻接矩阵的一行）。

• • 所以，使用邻接矩阵实现的 Dijkstra 算法的时间复杂度为 \( O(V^2) \) 。

• 使用优先队列（如最小堆）优化：

• • 每次从优先队列中取出距离最小的顶点的时间复杂度为 \( O(\log V) \) ，总共需要进行 \( V \) 次这样的操作，这部分的时间复杂度为 \( O(V\log V) \) 。

• • 对于图中的每条边 \( (u, v) \) ，更新顶点 \( v \) 的距离操作最多执行一次，由于边的数量为 \( E \) ，每次更新操作涉及到将顶点加入优先队列或调整优先队列，时间复杂度为 \( O(\log V) \) ，所以这部分的时间复杂度为 \( O(E\log V) \) 。

• • 综合起来，使用优先队列优化的 Dijkstra 算法的时间复杂度为 \( O((E + V)\log V) \) ，当图是稀疏图（即 \( E \ll V^2 \) ）时，这种优化方式能显著提高算法效率。

4. Bellman - Ford 算法

4.1 算法思想

Bellman - Ford 算法由美国数学家理查德・贝尔曼（Richard Bellman）和莱斯特・福特（Lester Ford）提出，是一种用于求解带权有向图中，从一个给定源点到其他所有顶点的最短路径的经典算法 。该算法基于动态规划思想，通过不断对图中的边进行松弛操作，逐步逼近最短路径。与 Dijkstra 算法不同，Bellman - Ford 算法能够处理包含负权边的图 。

其核心思想是对图中的每条边进行多次松弛操作。松弛操作是指对于一条边 \( (u, v) \) ，如果通过顶点 \( u \) 到达顶点 \( v \) 的距离比当前已知的顶点 \( v \) 到源点的距离更短，就更新顶点 \( v \) 到源点的距离。由于在一个具有 \( n \) 个顶点的图中，任意一条最短路径最多包含 \( n - 1 \) 条边（不考虑负权环的情况），所以 Bellman - Ford 算法通过对所有边进行 \( n - 1 \) 次松弛操作，就可以得到从源点到其他所有顶点的最短路径（如果图中不存在负权环） 。如果在 \( n - 1 \) 次松弛操作后，还能通过某条边进行松弛，那就说明图中存在负权环，此时最短路径不存在，因为可以通过负权环无限次地减小路径长度。

4.2 具体步骤

1. 初始化：

• • 设定源点 \( s \) 。

• • 初始化距离数组 \( dist \) ， \( dist[i] \) 表示从源点 \( s \) 到顶点 \( i \) 的当前最短距离，初始时 \( dist[s]=0 \) ，对于其他顶点 \( i \) ， \( dist[i]=\infty \) 。

• • 初始化路径数组 \( path \) ， \( path[i] \) 用于记录从源点 \( s \) 到顶点 \( i \) 的最短路径上 \( i \) 的前驱顶点，初始时 \( path[i]= - 1 \) 。

1. 松弛操作：

• • 对图中的每条边 \( (u, v) \) ，进行 \( n - 1 \) 次松弛操作（ \( n \) 为图中顶点的数量）。

• • 在每次松弛操作中，如果 \( dist[u] \neq \infty \) 且 \( dist[u]+w(u, v)\lt dist[v] \) （其中 \( w(u, v) \) 表示边 \( (u, v) \) 的权值），则更新 \( dist[v] \) 和 \( path[v] \) ：

• • • \( dist[v]=dist[u]+w(u, v) \) 。

• • • \( path[v]=u \) 。

1. 检测负权环：

• • 再对图中的每条边 \( (u, v) \) 进行一次松弛操作。

• • 如果在这次松弛操作中，存在某条边使得 \( dist[u] \neq \infty \) 且 \( dist[u]+w(u, v)\lt dist[v] \) ，则说明图中存在负权环，返回错误信息，表明不存在最短路径；否则， \( dist \) 数组中存储的就是从源点 \( s \) 到其他所有顶点的最短路径长度，通过 \( path \) 数组可以回溯得到具体的最短路径。

4.3 代码实现（以 Python 为例）

def bellman_ford(graph, source):

# 初始化距离字典，设为无穷大

distances = {vertex: float('infinity') for vertex in graph}

distances[source] = 0

# 进行|V|-1次松弛操作

for _ in range(len(graph) - 1):

for u in graph:

for v, weight in graph[u].items():

if distances[u] != float('infinity') and distances[u] + weight < distances[v]:

distances[v] = distances[u] + weight

# 检测负权环

for u in graph:

for v, weight in graph[u].items():

if distances[u] != float('infinity') and distances[u] + weight < distances[v]:

print("图中存在负权环，不存在最短路径")

return

return distances

# 示例图，使用邻接表表示

graph = {

'A': {'B': 1, 'C': 4},

'B': {'C': 2, 'D': 5},

'C': {'D': 1},

'D': {}

}

# 计算从节点'A'开始的最短路径

shortest_paths = bellman_ford(graph, 'A')

print(shortest_paths)

代码解释：

1. 首先创建一个 distances 字典，用于存储每个顶点到源点的距离，初始时除源点外，其他顶点的距离都设为无穷大。

1. 通过外层循环进行 \( n - 1 \) 次松弛操作，内层循环遍历图中的每条边进行松弛。

1. 最后再进行一次额外的循环来检测负权环，如果检测到负权环，则打印提示信息并返回。

1. 如果没有检测到负权环，则返回 distances 字典，其中包含了从源点到各个顶点的最短距离。

4.4 时间复杂度分析

Bellman - Ford 算法的时间复杂度为 \( O(VE) \) ，其中 \( V \) 是图中顶点的数量， \( E \) 是图中边的数量。原因如下：

• 算法需要对每条边进行 \( n - 1 \) 次松弛操作，而每次松弛操作都要遍历所有的边，遍历所有边的时间复杂度为 \( O(E) \) ，进行 \( n - 1 \) 次这样的操作，所以这部分的时间复杂度为 \( O((n - 1)E) \) ，由于 \( n - 1 \) 和 \( n \) 是同阶的，所以可以近似看作 \( O(VE) \) 。

• 最后检测负权环时，也需要遍历所有的边，这部分的时间复杂度同样为 \( O(E) \) 。相对于前面的 \( O(VE) \) ，这部分时间复杂度可以忽略不计 。所以总的时间复杂度为 \( O(VE) \) 。这种时间复杂度在图中边的数量较多时，计算效率相对较低，尤其是与使用优先队列优化后的 Dijkstra 算法相比，在处理没有负权边的图时，Bellman - Ford 算法的效率劣势更为明显。

5. SPFA 算法

5.1 算法思想

SPFA（Shortest Path Faster Algorithm）算法由西南交通大学段凡丁于 1994 年发表，是 Bellman - Ford 算法的一种队列优化 ，用于求解单源最短路径问题，该算法能够处理带有负权边的情况，在某些情况下比 Dijkstra 算法更高效 。

SPFA 算法的核心思想是设立一个队列用来保存待优化的顶点，优化时每次取出队首顶点 \( u \) ，并且用 \( u \) 点当前的最短路径估计值 \( dist[u] \) 对与 \( u \) 点邻接的顶点 \( v \) 进行松弛操作，如果 \( v \) 点的最短路径估计值 \( dist[v] \) 可以更小，且 \( v \) 点不在当前的队列中，就将 \( v \) 点放入队尾 。这样不断从队列中取出顶点来进行松弛操作，直至队列空为止 。通过这种方式，减少了 Bellman - Ford 算法中对一些不必要边的松弛操作，提高了算法效率 。并且其检测负权回路的方法也很简单，如果某个点进入队列的次数大于等于 \( n \) （ \( n \) 为图的顶点数），则存在负权回路 。

5.2 具体步骤

1. 初始化：

• • 设定源点 \( s \) 。

• • 初始化距离数组 \( dist \) ， \( dist[i] \) 表示从源点 \( s \) 到顶点 \( i \) 的当前最短距离，初始时 \( dist[s]=0 \) ，对于其他顶点 \( i \) ， \( dist[i]=\infty \) 。

• • 初始化一个布尔数组 \( in\_queue \) ，用于标记顶点是否在队列中，初始时所有顶点都不在队列中，即 \( in\_queue[i]=False \) 。

• • 初始化一个计数器数组 \( count \) ，用于记录每个顶点入队的次数，初始时 \( count[i]=0 \) 。

• • 创建一个队列 \( Q \) ，并将源点 \( s \) 加入队列，同时标记 \( s \) 在队列中，即 \( in\_queue[s]=True \) ， \( count[s]=1 \) 。

1. 松弛操作与队列更新：

• • 当队列 \( Q \) 不为空时，取出队首顶点 \( u \) ，并标记 \( u \) 不在队列中，即 \( in\_queue[u]=False \) 。

• • 遍历顶点 \( u \) 的所有邻接顶点 \( v \) ：

• • • 计算通过顶点 \( u \) 到达顶点 \( v \) 的新距离 \( new\_distance = dist[u]+w(u, v) \) ，其中 \( w(u, v) \) 表示边 \( (u, v) \) 的权值。

• • • 如果 \( new\_distance \lt dist[v] \) ，则更新 \( dist[v]=new\_distance \) 。

• • • 如果 \( v \) 不在队列中（即 \( in\_queue[v]=False \) ），则将 \( v \) 加入队列，标记 \( v \) 在队列中（即 \( in\_queue[v]=True \) ），并将 \( v \) 的入队次数加 1（即 \( count[v]++ \) ）。

• • • 如果某个顶点 \( v \) 的入队次数 \( count[v] \geq n \) （ \( n \) 为图中顶点的数量），则说明图中存在负权环，返回错误信息，表明不存在最短路径。

1. 结果返回：

• • 当队列 \( Q \) 为空且没有检测到负权环时， \( dist \) 数组中存储的就是从源点 \( s \) 到其他所有顶点的最短路径长度，通过回溯前驱节点（如果有记录前驱节点的数组）可以得到具体的最短路径。

5.3 代码实现（以 Python 为例）

from collections import deque

def spfa(graph, start):

n = len(graph)

# 初始化距离数组，设为无穷大

dist = [float('infinity')] * n

dist[start] = 0

# 标记节点是否在队列中

in_queue = [False] * n

# 记录节点入队次数，用于检测负权环

count = [0] * n

queue = deque([start])

in_queue[start] = True

count[start] = 1

while queue:

u = queue.popleft()

in_queue[u] = False

for v, weight in enumerate(graph[u]):

if weight > 0: # 存在边

new_distance = dist[u] + weight

if new_distance < dist[v]:

dist[v] = new_distance

if not in_queue[v]:

queue.append(v)

in_queue[v] = True

count[v] += 1

if count[v] >= n:

print("图中存在负权环，不存在最短路径")

return

return dist

# 示例图，使用邻接矩阵表示

graph = [

[0, 1, 4, float('infinity'), float('infinity')],

[1, 0, 2, 5, float('infinity')],

[4, 2, 0, 1, float('infinity')],

[float('infinity'), 5, 1, 0, float('infinity')],

[float('infinity'), float('infinity'), float('infinity'), float('infinity'), 0]

]

# 计算从节点0开始的最短路径

shortest_paths = spfa(graph, 0)

print(shortest_paths)

代码解释：

1. 首先创建一个 dist 列表，用于存储每个顶点到源点的距离，初始时除源点外，其他顶点的距离都设为无穷大。

1. 使用 deque 创建一个队列 queue ，并将源点加入队列，同时标记源点在队列中，记录源点入队次数。

1. 在循环中，不断从队列中取出顶点，遍历其邻接顶点进行松弛操作。如果通过当前顶点到达邻接顶点的距离更短，则更新邻接顶点的距离，并将其加入队列（如果不在队列中），同时更新入队次数。

1. 如果某个顶点的入队次数超过顶点数，则说明存在负权环，打印提示信息并返回。

1. 最后返回 dist 列表，其中包含了从源点到各个顶点的最短距离。

5.4 时间复杂度分析

• 最佳时间复杂度：当图是一个类似于链状的结构，且源点位于链的一端时，每个顶点只入队一次，此时时间复杂度为 \( O(n) \) ，其中 \( n \) 是图中顶点的数量 。因为只需要对每个顶点进行一次出队和相关的松弛操作。

• 平均时间复杂度：对于一个随机图，运用均摊分析的思想，每个点的平均出度为 \( O(\frac{m}{n}) \) （ \( m \) 为边的数量），而每个点的平均入队次数为 2 （虽然 2 这个数字的严格证明较难，但在实际情况和研究中一般认为是这样 ），因此时间复杂度为 \( O(n\cdot\frac{m}{n}\cdot2)=O(2m)=O(m) \) ，即与边的数量成正比 。

• 最坏时间复杂度：在一个完全图中，且边权的设置使得每次更新完一个顶点出队后，另一个顶点都可以再次对其进行更新并入队，例如在一个有 \( n \) 个顶点的完全图中，从源点开始，每次更新完顶点 \( k \) 出队后，顶点 \( k + 1 \) 都可以再次对顶点 \( k \) 进行更新并入队 （ \( 1\leq k\leq n - 2 \) ） 。那么 0 点入队 1 次；1 点入队 \( n - 1 \) 次；2 点入队 \( n - 2 \) 次；……； \( n - 2 \) 点入队 2 次； \( n - 1 \) 点入队 1 次 。因为是完全图，每个点的出度为 \( n - 1 \) ，所以总的时间复杂度为 \( (n - 1)\cdot[1 + 1+2 + 3+\cdots+(n - 2)+(n - 1)]=O(n^3) \) ，由于在完全图中 \( m = O(n^2) \) ，所以也可以表达成 \( O(nm) \) 。这也是为什么在 NOI2018Day1T1 归程中，出题人构造了特殊的数据，使得 SPFA 算法被卡，时间复杂度退化为最坏情况，导致原本能得 100 分的算法只能得到 60 分 。所以在没有负环、单纯求最短路径时，如果没有特殊情况，不建议使用 SPFA 算法，而是优先选择 Dijkstra 算法 。

6. 算法比较与选择

在实际应用中，选择合适的单源最短路径算法至关重要，它直接影响到程序的运行效率和资源消耗。我们可以从适用场景、时间复杂度和空间复杂度等方面对 Dijkstra 算法、Bellman - Ford 算法和 SPFA 算法进行比较 。

6.1 适用场景

• Dijkstra 算法：适用于边权非负的图。由于其贪心的本质，一旦确定了某个顶点的最短路径，就不会再改变 。如果图中存在负权边，可能会导致错误的结果。例如在地图导航中，道路的距离或行驶时间通常是非负的，这种情况下 Dijkstra 算法是一个很好的选择 。

• Bellman - Ford 算法：能够处理含有负权边的图，并且可以检测图中是否存在负权环。在一些金融套利场景中，可能会出现负权边（例如存在汇率差异导致的套利机会），此时 Bellman - Ford 算法可以用于寻找最优的套利路径 。如果检测到负权环，说明存在可以无限获利的套利机会，但在实际中这种情况可能需要特殊处理，因为它可能不符合实际的市场规则 。

• SPFA 算法：同样适用于含有负权边的图，是 Bellman - Ford 算法的优化。在平均情况下，其时间复杂度优于 Bellman - Ford 算法 。但在最坏情况下，时间复杂度会退化到与 Bellman - Ford 算法相同，甚至更差 。所以在使用 SPFA 算法时，需要考虑数据的特点，避免遇到最坏情况 。例如在一些稀疏图且存在负权边的场景中，SPFA 算法可能会有较好的表现 。

6.2 时间复杂度

• Dijkstra 算法：使用邻接矩阵实现时，时间复杂度为 \( O(V^2) \) ；使用优先队列（如最小堆）优化后，时间复杂度为 \( O((E + V)\log V) \) 。在稀疏图（ \( E \ll V^2 \) ）中，优先队列优化后的 Dijkstra 算法效率更高 。例如在一个具有大量顶点但边相对较少的网络拓扑图中，使用优化后的 Dijkstra 算法可以显著减少计算时间 。

• Bellman - Ford 算法：时间复杂度为 \( O(VE) \) 。由于每次迭代都需要遍历所有边，当图中边的数量较多时，计算效率相对较低 。比如在一个完全图中，边的数量 \( E = V(V - 1)/2 \) ，此时 Bellman - Ford 算法的时间复杂度会非常高 。

• SPFA 算法：最佳时间复杂度为 \( O(n) \) ，平均时间复杂度为 \( O(m) \) ，最坏时间复杂度为 \( O(nm) \) 。虽然在平均情况下表现较好，但由于最坏时间复杂度较高，在一些竞赛或对时间复杂度要求严格的场景中，需要谨慎使用 。

6.3 空间复杂度

• Dijkstra 算法：主要需要额外的空间来存储距离数组（大小为 \( V \) ，存储从起点到每个节点的最短距离）、已访问集合（同样大小为 \( V \) ）以及优先队列（取决于实现，但常用的数据结构如二叉堆空间复杂度为 \( O(\log V) \) ） 。所以，空间复杂度为 \( O(V + \log V) \) ，近似看作 \( O(V) \) 。

• Bellman - Ford 算法：需要存储距离数组（大小为 \( V \) ）和路径数组（大小为 \( V \) ） ，空间复杂度为 \( O(V) \) 。

• SPFA 算法：需要存储距离数组（大小为 \( V \) ）、布尔数组（大小为 \( V \) ，用于标记顶点是否在队列中）、计数器数组（大小为 \( V \) ，用于记录每个顶点入队的次数）以及队列（大小最多为 \( V \) ） ，空间复杂度为 \( O(V) \) 。

综上所述，在选择算法时，如果图中没有负权边，优先考虑使用 Dijkstra 算法，特别是当图是稀疏图时，使用优先队列优化的 Dijkstra 算法能获得更高的效率；如果图中存在负权边，且对算法的最坏情况时间复杂度有严格要求，或者需要检测负权环，Bellman - Ford 算法是一个可靠的选择；而 SPFA 算法在平均情况下表现良好，但要注意其最坏情况时间复杂度的风险，在合适的场景下（如稀疏图且存在负权边，并且对最坏情况时间复杂度不太敏感时）可以使用 。

7. 总结

单源最短路径问题在现实生活和学术研究中都具有极其重要的地位，它为众多领域提供了关键的解决方案 。Dijkstra 算法、Bellman - Ford 算法和 SPFA 算法作为解决该问题的主要算法，各自具有独特的特点和适用场景。

Dijkstra 算法基于贪心思想，在边权非负的图中表现出色，通过优先队列优化后，在稀疏图中能高效地找到最短路径；Bellman - Ford 算法基于动态规划思想，能够处理含有负权边的图，并且可以检测负权环，虽然时间复杂度较高，但在一些特定场景下不可或缺；SPFA 算法是 Bellman - Ford 算法的队列优化，在平均情况下效率较高，但要警惕最坏情况时间复杂度的退化 。

在实际应用中，我们需要根据图的性质（是否含有负权边）、数据规模（顶点和边的数量）以及对时间复杂度和空间复杂度的要求等因素，综合选择合适的算法 。同时，随着技术的不断发展和实际问题的日益复杂，未来可能会出现更高效、更通用的单源最短路径算法，这也值得我们持续关注和研究 。希望读者通过本文对单源最短路径算法有更深入的理解，并能够将其应用到实际的项目和问题解决中 。