论文基本信息

• 题目: Rethinking Smoothness for Fast and Adaptable Entity Alignment Decoding (为快速和自适应的实体对齐解码重新思考平滑性)
• 作者: Yuanyi Wang, Han Li, Haifeng Sun, Lei Zhang, Bo He, Wei Tang, Tianhao Yan, Qi Qi, Jingyu Wang
• 机构:
  1. 北京邮电大学，网络与交换技术国家重点实验室
  2. 中国联通网络通信有限公司
  3. 华为翻译服务中心
  4. 吉林大学
• 发表地点与年份: Findings of the Association for Computational Linguistics: NAACL 2025
• 关键词术语与定义:
  • Knowledge Graphs (KGs): 以三元组 $(h,r,t)$ 形式存储结构化知识的图，其中 $h$ 和 $t$ 是实体，$r$ 是关系。
  • Entity Alignment (EA): 识别并对齐来自不同知识图谱的等价实体的任务。
  • Encoder-Decoder Architecture: EA 的一种典型架构，编码器负责生成实体和关系的嵌入表示，解码器负责利用这些嵌入来建立对齐。
  • Smoothness (平滑性): 在图嵌入空间中，相邻节点的特征或表示应尽可能相似。本文通过最小化狄利克雷能量 (Dirichlet Energy) 来最大化平滑性。
  • Triple Feature Propagation (TFP): 本文提出的一个快速、自适应的实体对齐解码框架，它仅利用实体嵌入，通过最大化平滑性来重构知识图谱表示。

摘要（详细复述）

• 背景: 实体对齐 (EA) 对于整合多源知识图谱至关重要，其目标是识别不同图谱中的等价实体。现有的大多数 EA 解码方法依赖于实体和关系两种嵌入，这限制了它们在 GNN-based 模型中的通用性和效率。
• 方案概述: 为解决这些挑战，论文提出了 Triple Feature Propagation (TFP) 框架。这是一个自适应且快速的 EA 解码方法，它创新地只使用实体嵌入。TFP 的核心思想是通过最大化实体嵌入的平滑性来重构 KG 的表示。该过程通过一个离散化的平滑性最大化过程实现，并推导出显式的欧拉解。此外，为了捕捉图谱的结构多样性，论文泛化了多种视图矩阵，包括实体-实体、实体-关系、关系-实体和关系-三元组矩阵。
• 主要结果/提升: 在多个公开数据集上的大量实验表明，TFP 框架具有快速和对不同编码器自适应的优点。它能够在 6 秒内取得与当前最先进方法相当的结果，并且在许多情况下超越了它们。
• 结论与意义: TFP 提供了一个高效、通用且理论基础坚实的解码方案，它摆脱了对关系嵌入的依赖，显著提升了解码阶段的效率，并为实体对齐领域提供了一个新的视角。

研究背景与动机

• 学术/应用场景与痛点: 知识图谱 (KGs) 在自然语言处理中扮演着核心角色，但单个 KG 往往存在覆盖不全的问题。通过实体对齐整合多个 KGs 可以获得更完整、互补的知识。然而，现有的 EA 方法，尤其是在解码阶段，存在两大痛点：1) 效率低下：一些解码器计算复杂度高，耗时严重。2) 通用性差：许多解码器（如 DATTI）强依赖于关系嵌入，而很多先进的 GNN-based 编码器并不直接产出关系嵌入，导致解码器无法适用。

• 主流路线与代表工作:

  • 编码器 (Encoder):
    1. 翻译模型 (Translation-based): 如 TransE 及其变体，将关系视为头实体到尾实体的翻译向量。
    2. 图神经网络模型 (GNN-based): 如 GCN-Align 和 Dual-AMN，通过聚合邻居信息来生成实体表示。
  • 解码器 (Decoder):
    1. 局部/贪心策略: 如 CSLS，计算实体对的相似度并进行局部匹配，速度快但可能忽略全局结构。
    2. 全局对齐策略: 如匈牙利算法 (Hungarian algorithm) 和 Sinkhorn 算法，寻求全局最优匹配，但通常忽略 KG 的结构特性。
    3. 结构化解码: 如 DATTI 和 LightEA，尝试利用 KG 的结构信息进行解码，但存在前述的效率或通用性问题。

• 代表工作与局限总结:

方法	优点	不足
CSLS	简单、快速。	仅考虑局部相似性，未充分利用图结构。
Hungarian/Sinkhorn	提供全局一对一匹配。	计算开销大，且未利用 KG 的结构特性。
DATTI	利用高阶张量同构捕捉结构信息，精度高。	依赖关系嵌入，不适用于仅输出实体嵌入的编码器（如 RREA）；计算耗时。
LightEA	解码框架适应性强。	计算开销仍然很大，在实践中不够高效。

问题定义（形式化）

• 输入:

  • 源知识图谱 $G_s=(E_s,R_s,T_s)$。
  • 目标知识图谱 $G_t=(E_t,R_t,T_t)$。
  • 其中 $E$ 是实体集，$R$ 是关系集，$T$ 是三元组集。
  • 一组预对齐的种子实体对 (seed alignments)。
  • 由编码器生成的初始实体嵌入 $X^{(0)}\in {\mathbb{R}}^{|E|\times d}$。

• 输出:

  • 一个一对一的映射函数 $\Phi =\{(e_s,e_t)|e_s\in E_s,e_t\in E_t,e_s\equiv e_t\}$，表示源和目标图谱中等价的实体对。

• 约束与目标函数:

  • 核心目标是最大化实体嵌入的平滑性，这等价于最小化图上的狄利克雷能量 (Dirichlet Energy, DE)。
  • 给定图节点嵌入 $X\in {\mathbb{R}}^{N\times d}$，其狄利克雷能量定义为：
    $$\mathcal{L}(X)=\text{tr}(X^T\Delta X)=\frac{1}{2}\sum _{i,j=1}^N{a}_{ij}{\Vert \frac{X_i}{\sqrt{D_{i,i}+1}}-\frac{X_j}{\sqrt{D_{j,j}+1}}\Vert }^2$$
    其中 $\Delta =I-\tilde{A}$ 是对称归一化拉普拉斯矩阵，$\tilde{A}=D^{-1/2}A{D}^{-1/2}$ 是对称归一化邻接矩阵，$A$ 是邻接矩阵，$D$ 是度矩阵。
  • 在解码过程中，种子对齐实体 $E_s$ 的特征 $x_s$ 保持不变，作为边界条件。

• 评测目标: 使用 Hits@k 和 MRR 指标来评估对齐的准确性。

创新点（逐条可验证）

1. 基于平滑性最大化的解码新范式: 论文首次将图信号处理中的平滑性概念（通过最小化狄利克雷能量实现）作为实体对齐解码的核心驱动力。这提供了一个坚实的数学基础，将解码过程形式化为一个梯度流问题，从而推导出迭代解法。如何做：通过迭代传播过程更新非种子实体的嵌入，使其在特征空间中向其邻居（尤其是已对齐的种子实体）平滑过渡。为什么有效：该方法利用图的内在结构（同质性），使得等价实体在嵌入空间中更加接近，且不依赖于关系嵌入，通用性强。

2. 泛化的多视图矩阵: 论文没有局限于传统的实体-实体邻接矩阵，而是提出了多种捕捉 KG 丰富结构信息的视图矩阵。如何做：定义了实体-关系矩阵 ($A^{\text{proximal}}$)、关系-实体矩阵 ($A^{\text{distal}}$)、加权实体-实体矩阵 ($A^{\text{integral}}$) 和关系-三元组矩阵 ($A^{\text{tri-rel}}$)。为什么有效：这些矩阵从不同角度描述了 KG 的元结构，如 “(London, CapitalOf, England)”，传统邻接矩阵只能表示 London 和 England 相连，而 $A^{\text{proximal}}$ 可以捕捉 London 到 CapitalOf 的链接，$A^{\text{integral}}$ 可以通过统计共现次数区分不同关系下的连接。这使得 TFP 能够捕捉比传统方法更全面的结构信息。

3. 高效的显式欧拉解法: 论文将复杂的梯度流微分方程离散化，得到了一个极其简单高效的迭代算法。如何做：通过将时间导数近似为前向差分，并设步长 $h=1$，推导出了核心迭代公式 $X^{(k+1)}\leftarrow \tilde{A}{X}^{(k)}$。为什么有效：该迭代过程仅涉及稀疏矩阵乘法，计算成本极低，使得 TFP 能够在数秒内完成解码，远快于其他结构化解码方法。

方法与核心思路（重点展开）

整体框架

TFP 框架是一个解码器，它接收编码器产生的初始实体嵌入，并通过一个迭代的传播过程来优化这些嵌入，最终用于对齐。其核心思想是，在一个平滑的嵌入空间中，结构上相似的实体（即等价实体）应该具有相似的表示。TFP 通过模拟一个在图上最小化狄利克雷能量的梯度流过程来实现这一点。该过程被泛化，以利用多种结构视图矩阵，从而实现更全面的信息传播。

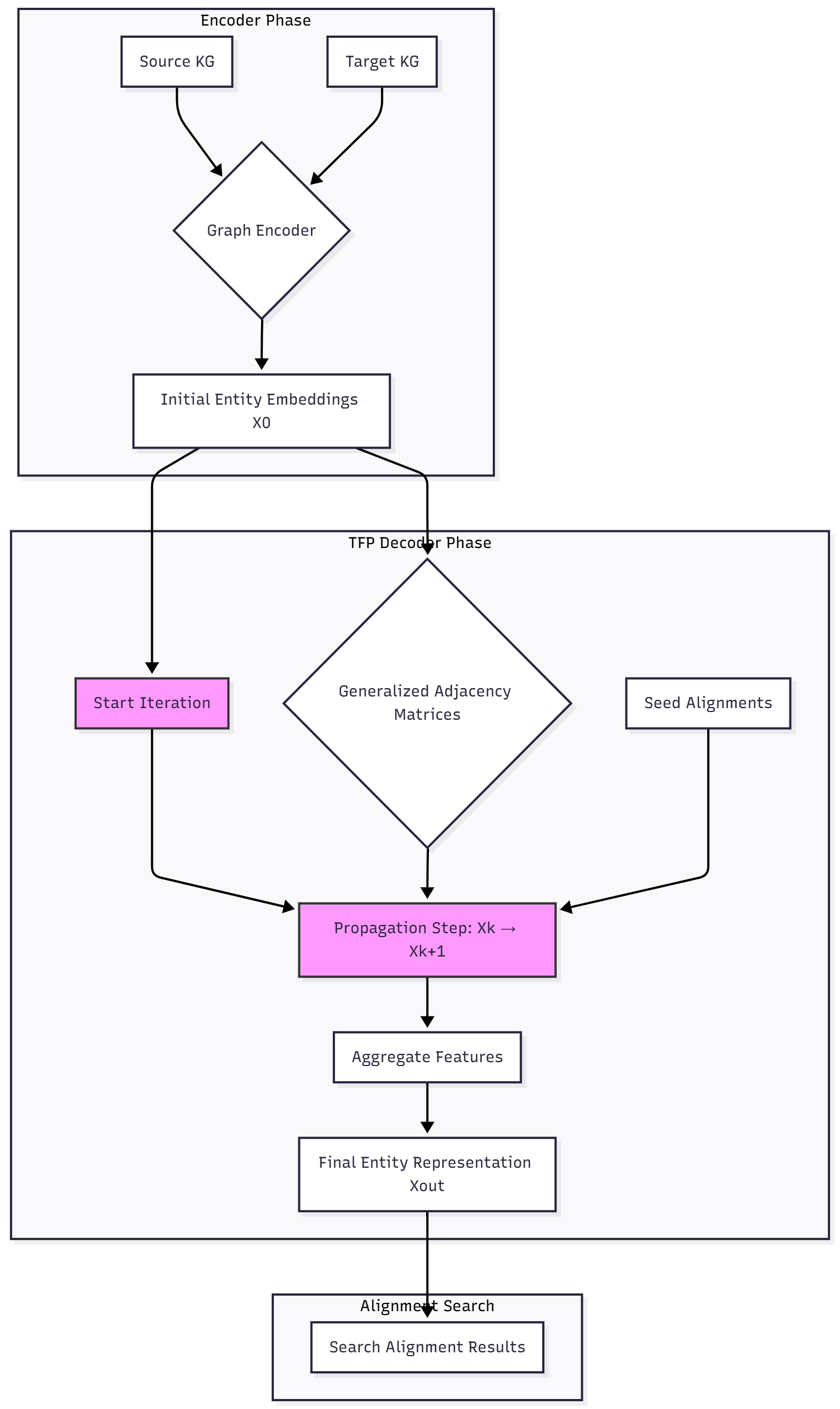
步骤分解与模块交互

1. 理论基础：平滑性与狄利克雷能量

   • TFP 的目标是找到一组实体嵌入 $X$，使得狄利克雷能量 $\mathcal{L}(X)$ 最小。当 $\mathcal{L}(X)$ 很小时，意味着相邻节点的嵌入向量非常相似，即嵌入是“平滑”的。
   • 将实体集划分为种子实体 $E_s$ (特征为 $x_s$) 和其他实体 $E_o$ (特征为 $x_o$)。
   • 该优化问题可以看作一个梯度流过程，由微分方程描述：
     $$\frac{dx(t)}{dt}=-{\nabla }_x\mathcal{L}(X(t))=-\Delta X(t)$$
     其中边界条件为 $x_s(t)=x_s$ (种子实体特征不变)。
   • 该方程的稳态解（即 $\frac{d{x}_o(t)}{dt}=0$）为 $x_o(\infty )=-{\Delta }_{oo}^{-1}{\Delta }_{os}{x}_s$，但这需要矩阵求逆，计算成本为 $O(|E{|}^3)$，不切实际。

2. 数值解：显式欧拉方案

   • 为避免矩阵求逆，论文采用迭代法求解。将微分方程离散化，使用步长 $h=1$ 的显式欧ラ方案：
     $$X^{(k+1)}=X^{(k)}+h\frac{dX(t)}{dt}{|}_{t=k}=X^{(k)}-\Delta X^{(k)}=(I-\Delta )X^{(k)}=\tilde{A}{X}^{(k)}$$
     其中 $\tilde{A}$ 是对称归一化邻接矩阵。
   • 在每一步迭代后，需要重置种子实体的嵌入以满足边界条件。最终，基础 TFP 的迭代公式为：
     $$X^{(k+1)}\leftarrow \tilde{A}{X}^{(k)};x_s^{(k+1)}\leftarrow x_s^{(0)}$$
     这个简单的迭代过程构成了 TFP 的核心。

3. 泛化：多视图矩阵

   • 为了捕捉 KG 中超越简单邻接关系的复杂结构，论文定义了多个视图矩阵。
   • (i) 实体-关系矩阵 $A^{\text{proximal}}$: 描述从头实体 $h$ 到关系 $r$ 的有向连接。例如，对于 (London, CapitalOf, England)，存在从 London 到 CapitalOf 的链接。
   • (ii) 关系-实体矩阵 $A^{\text{distal}}$: 描述从关系 $r$ 到尾实体 $t$ 的有向连接。
   • (iii) 加权实体-实体矩阵 $A^{\text{integral}}$: 这是一个加权的邻接矩阵，其权重 $A_{i,j}^{\text{integral}}$ 表示连接实体 $h_i$ 和 $t_j$ 的三元组数量。这可以区分不同关系下的连接强度。
   • (iv) 关系-三元组矩阵 $A^{\text{tri-rel}}$: 描述关系 $r$ 与包含它的三元组 $T_i$ 之间的关系。
   • 这些矩阵经过归一化处理后，可以像基础 TFP 中的 $\tilde{A}$ 一样，用于特征传播。

4. 完整 TFP 算法流程

   • 传播过程:
     • 首先，关系特征通过关系-实体矩阵传播到实体上：$X_e^{(k)}={\tilde{A}}^{\text{distal}}{X}_r^{(k)}$。
     • 然后，实体特征通过加权实体-实体矩阵和实体-关系矩阵进行更新：$X_e^{(k+1)}={\tilde{A}}^{\text{integral}}{X}_e^{(k)}+{\tilde{A}}^{\text{proximal}}{X}_r^{(k)}$。
     • 种子实体特征被重置：$x_s^{(k+1)}\leftarrow x_s^{(0)}$。
   • 三元组特征构建:
     • 在 $K$ 轮迭代后，每一步的实体特征被拼接起来，形成一个聚合的实体表示 $X_e=[X^{(0)}||X^{(1)}||\dots ||X^{(K)}]$。
     • 关系特征 $X_r$ 与关系-三元组矩阵 $A^{\text{tri-rel}}$ 相乘，得到三元组的隐式表示 $X_t=A^{\text{tri-rel}}{X}_r$。
     • 为了控制维度和计算成本，使用随机投影将 $X_e$ 和 $X_r$ 的维度分别降低到 $d_e$ 和 $d_r$。
   • 最终表示:
     • 降维后的三元组特征 $X_t$ 被视为 $d_r$ 个不同的“关系切片”。每个切片 $X_t(i)$ 定义了一个新的实体-实体邻接关系 $A_i^{\text{triple}}$。
     • 降维后的实体特征 ${\bar{x}}_e$ 在这 $d_r$ 个新的图结构上传播：$X_i=A_i^{\text{triple}}{\bar{x}}_e,i=1,\dots ,d_r$。
     • 最终的实体表示是所有这些传播结果的拼接：$X_{\text{out}}=[X_1||X_2||\dots ||X_{d_r}]$。

伪代码

以下是论文中 Algorithm 1 的伪代码及其解释：

Algorithm 1: TFP

Input: 初始实体嵌入 X^(0), 三元组 T, 迭代次数 K, 维度 d_r, d_e
Output: 重构后的实体特征 X_out

1: Initialize A_proximal, A_distal, A_integral, and A_tri-rel from triples T
2: for k = 1 -> K do
3:   X_r^(k) <- A_distal * X_e^(k)
4:   X_e^(k+1) <- A_integral * X_e^(k) + A_proximal * X_r^(k)
5:   x_s^(k+1) <- x_s^(0)
6: end for
7: X_r <- random_projection(X_r^(K), d_r)
8: X_t <- A_tri-rel * X_r
9: Generate A_triple through X_t
10: X_e <- random_projection(X_e^(K), d_e)
11: X_i <- A_i^triple * X_e
12: X_out <- [X_1 || X_2 || ... || X_{d_r}]
13: return X_out

• 伪代码解释:
  • 第1行: 根据三元组数据构建多视图邻接矩阵。
  • 第2-6行: 进行 $K$ 轮迭代传播。在每一轮中，特征在关系和实体之间双向流动，并重置种子实体特征。
  • 第7-10行: 迭代结束后，对最终的关系和实体特征进行随机投影降维。
  • 第8-9行: 利用关系特征和关系-三元组矩阵构建三元组特征，并将其作为新的图结构。
  • 第11-12行: 在新的三元组图结构上传播降维后的实体特征，并将所有结果拼接成最终的输出表示。

复杂度分析

• 时间复杂度: TFP 的核心是稀疏矩阵乘法。根据论文所述，优化的计算复杂度为 $O(K(|T|d_r+|E|d_e))$。其中 $K$ 是迭代次数，$|T|$ 是三元组数量，$|E|$ 是实体数量，$d_r,d_e$ 是降维后的维度。由于 $K,d_r,d_e$ 通常是小常数，复杂度主要由图谱的规模决定，远低于 $O(|E{|}^3)$。
• 空间复杂度: 主要由存储多视图矩阵和各阶段的嵌入向量决定。

关键设计选择

• 仅使用实体嵌入: 这是 TFP 最关键的设计之一。它使得该解码器能够与任何只生成实体嵌入的编码器（特别是许多 GNN 模型）无缝对接，极大地增强了通用性。
• 显式欧拉方案与步长 $h=1$: 选择这个方案是为了极致的效率。虽然可能在数值精度上不是最优解，但它将复杂的微分方程求解简化为简单的矩阵-向量乘法，使得算法非常快速。实验结果表明，这种近似在实践中是有效的。
• 多视图矩阵: 这是对 KG 结构信息进行深度挖掘的设计。单一的邻接矩阵无法区分不同关系下的连接，而多视图矩阵可以从不同维度捕捉结构信息，为平滑性传播提供了更丰富的路径。
• 随机投影: 在后期处理中引入随机投影是为了控制最终输出特征的维度，避免维度爆炸，同时加速计算。这是一种在保留主要信息的同时降低计算成本的常用技术。

实验设置

• 数据集:

  • DBP15K: 包含三个跨语言子集 (ZH-EN, JA-EN, FR-EN)，每个子集含 15,000 个对齐实体对。
  • SRPRS: 同样包含 15,000 个实体对，但三元组数量远少于 DBP15K，是稀疏图谱的代表。
  • 数据集划分：30% 的对齐实体对用于训练，70% 用于测试。

• 对比基线:

  • 编码器:
    • GNN-based: MRAEA, RREA, Dual-AMN (SOTA)
    • Translation-based: AlignE, RSN, TransEdge
  • 解码器:
    • Hungarian algorithm, Sinkhorn, DATTI (SOTA of EA decoder), LightEA

• 评价指标:

  • Hits@k: 前 k 个候选中正确实体的比例 (k=1, 10)。
  • MRR (Mean Reciprocal Rank): 正确实体排名的倒数的平均值。

• 实现细节:

  • 硬件: NVIDIA RTX A6000 GPU, Intel Xeon Gold 6248R CPU。
  • 超参数:
    • 编码器输出维度 $d$: 根据各自论文设置 (如 Dual-AMN 为 768, RSN 为 256)。
    • TFP 迭代次数 $K$: 根据实验，最佳值通常在 $K=2$ 左右。
    • TFP 降维维度: 关系维度 $d_r=512$，实体维度 $d_e=16$。
  • 推理耗时: 论文强调 TFP 的解码时间通常在 6 秒以内。

实验结果与分析

• 主结果分析:

  • 性能: TFP 在绝大多数编码器和数据集组合上都取得了显著的性能提升。它通常能获得“亚军”的位置，仅次于专门为特定编码器设计的、计算成本高得多的解码器。例如，在 Dual-AMN 编码器上，TFP 的结果与 SOTA 解码器 DATTI 非常接近，但在 RREA (不产生关系嵌入) 上，DATTI 无法使用，而 TFP 表现出色。
  • 效率: Table 2 和 Table 7 展示了 TFP 的巨大速度优势。在 GPU 上，解码时间通常在 4-6 秒之间，远快于 LightEA (约11-17秒) 和 DATTI (约4-8秒)。即使在 CPU 上，TFP 的速度也与基于 GPU 的匈牙利算法相当。
  • 自适应性: TFP 在 GNN-based 和 Translation-based 两类编码器上都表现良好，证明了其强大的自适应能力和通用性。

• 消融实验 (超参数分析):

  • 传播轮数 K (Propagation Round): Figure 3 显示，性能在 $K=2$ 时达到峰值，之后会因“过平滑”问题而略有下降。这说明多视图矩阵能有效捕捉结构，但过多的传播会使节点特征趋于一致，丧失区分度。
  • 实体维度 $d_e$ 和关系维度 $d_r$: TFP 对这些维度的变化不敏感，即使在维度被大幅压缩后，性能也保持稳定。这表明随机投影是有效的，并且 TFP 的鲁棒性很好。

• 无监督文本解码:

  • 将 TFP 用于无监督场景（使用预训练的 GLoVe 词向量作为初始特征，无种子对齐），TFP 在 SRPRS 数据集上超越了所有基线，在 DBP15K 上也取得了极具竞争力的结果。这表明 TFP 的传播机制本身非常强大，能够有效利用图拓扑来优化初始嵌入。

• 实验数据表格总结 (以 DBPZH-EN 和 SRPRSDE-EN 为例):

编码器	解码器	DBPZH-EN (Hits@1/MRR)	SRPRSDE-EN (Hits@1/MRR)	解码时间(s, DBP15K)
DualAMN	(baseline)	83.43 / 88.14	61.20 / 68.30	-
	+DATTI	87.30 / 91.30	62.30 / 69.10	6.6
	+LightEA	84.45 / 89.10	61.38 / 68.86	13.4
	+TFP	85.31 / 89.92	61.84 / 69.01	5.1
TransEdge	(baseline)	76.90 / 83.03	55.65 / 64.28	-
	+DATTI	81.80 / 87.30	59.30 / 67.30	6.1
	+LightEA	80.68 / 87.30	64.80 / 71.24	12.5
	+TFP	82.36 / 87.91	64.12 / 70.95	4.7

复现性清单

• 代码/数据: 论文在第2页提供了 GitHub 链接：https://github.com/wyy-code/TFP。
• 模型权重: 未明确说明是否提供预训练模型权重。
• 环境与依赖: 未详细列出，但提到使用了 Tensorflow。
• 运行命令/配置文件: 未提供。
• 评测脚本: 预计包含在代码库中。
• 许可证与限制: 未说明。

结论与未来工作

• 结论: 论文成功地提出了一种快速、自适应且理论基础坚实的实体对齐解码算法 TFP。通过最大化实体嵌入的平滑性，TFP 显著提升了多种主流 EA 模型的性能，同时将解码时间缩短至 6 秒以内，解决了现有解码方法在效率和通用性上的痛点。

• 未来工作:

  • 性能与效率的权衡: 虽然 TFP 很快，但在某些数据集上与最顶级的（但很慢的）方法仍有微小差距。未来工作将致力于进一步提升精度，同时保持高效率。
  • 多模态实体对齐: 论文的实验仅限于单模态（结构化）数据。未来计划将 TFP 框架扩展到多模态场景（如包含图像、文本等信息的实体），只需使用多模态编码器生成初始嵌入即可。