重要性采样是RL强化学习，特别是调优LLM的PPO等的理论基础。

这里从蒙特卡洛的角度，尝试分析和探索重要性采样，重要分布，以及重要权重的核心要素。

所用到的图标、数据参考和修改自网络资料。

1 蒙特卡洛积分

重要性采样是蒙特卡洛积分的一种策略，在探索重要性采样之前，先来探索一下蒙特卡洛积分。

1.1 均匀采样估计

这里用采样的方式，模拟蒙特卡洛积分。

求函数 f(x) 在区间 [a, b] 上的积分时，如果积分曲线难以解析，那就无法直接求积分。

这时候可以采用估计方式，

即在区间 [a, b] 上进行采样： {x1, x2, ..., xn} 

值为 {f(x1), f(x2),...,f(xn)}。

 如果均匀采样的，采样结果如下图所示。

​

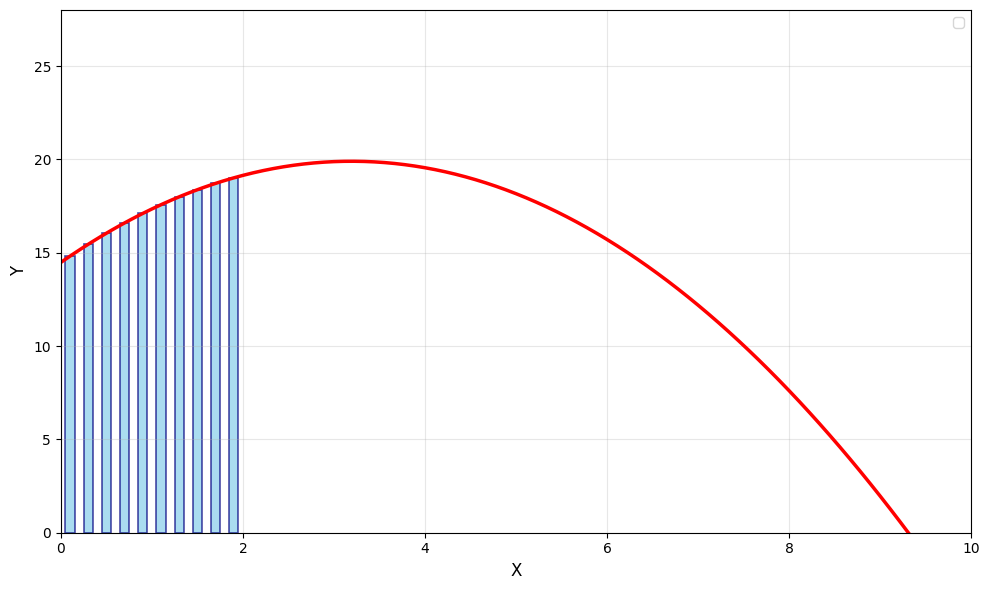
1.2 采样模拟积分

档采样的力度足够细，大致可以采用如下公式估计f(x)的积分。

这里(b-a)/N是上面小长方形的底部宽度，而f(xi)则是长方形的高。

当N足够大时，累加所有小长方形的面积，就能得到[a, b]区间内对f(x)积分的近似。

2 重要性采样

均匀采样的估计方法，随着取样数的增长，估计会越来越精确。

那是否有不需要那么多的样本数，同样可精确估计的方法，这就是这里探索的重要性采样。

2.1 重要性分布

比如如下图所示，通过人为对采样过程进行干预。

​

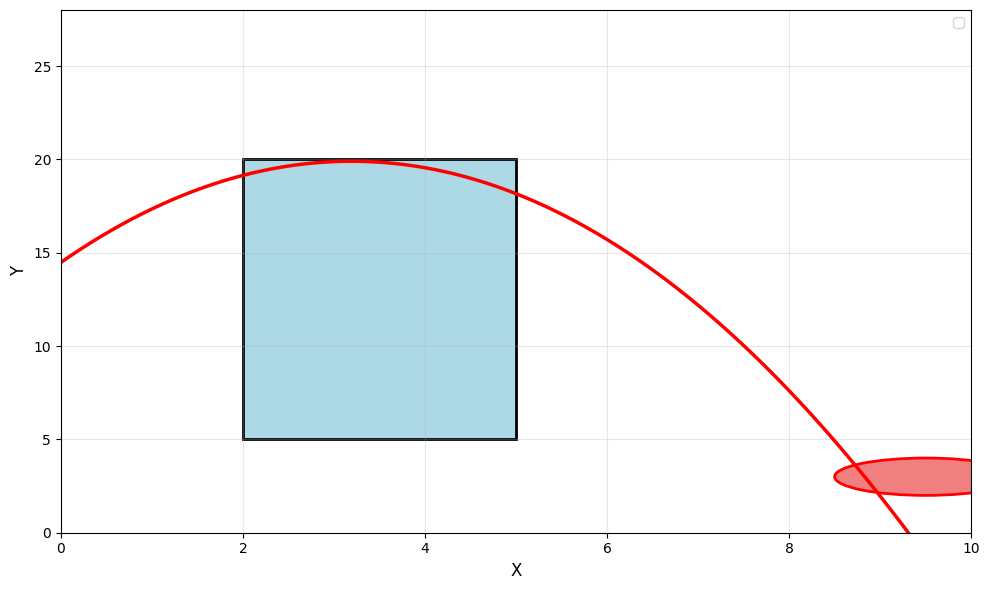
方形区域的函数值对积分的贡献比椭圆形区域要大很多，所以在抽样时，增加在方形区域的的抽样概率，就可以更快的提高估计的准确程度。

假设，一分布p(x)在原函数上进行采样。

​

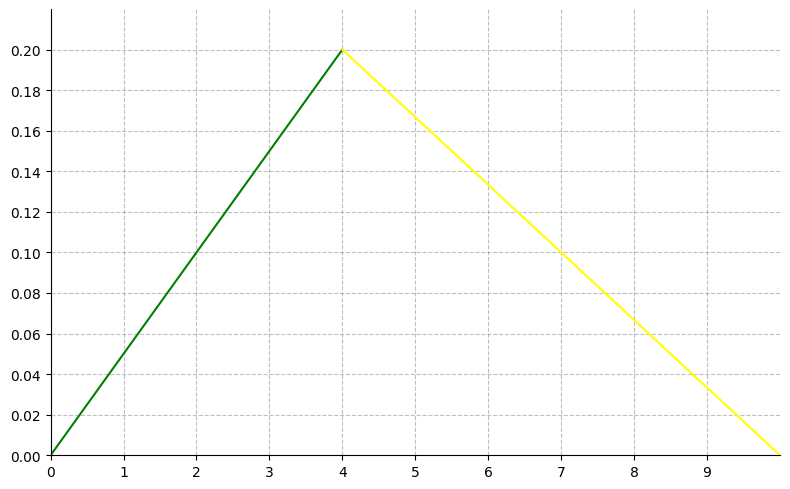
依照这个分布进行采样，一定程度上可以使得在原函数对积分贡献大的区域获得更多的采样机会。但这时不能对 {f(x1),f(x2),...,f(xn)} 进行简单的求和平均来获得估计值，因为此时采样不是均匀分布的，小矩形的“宽”并不等长，所以我们要对其进行加权，这个权重就是重要性权重，后文会讨论。

得到重要性权重之前，重新思考“为什么要引入一个新的分布 p(x) ”

原函数 f(x) 本身就是定义在一个分布之上的，定义这个分布为 π(x) 。

因为一些原因，无法直接从 π(x) 上进行采样，所以重新找到一个更加简明的分布 p(x) ，对它进行取样，希望间接地求出f(x)在分布 p(x) 下的期望。

比如，反常积分，被积函数无界，无界区域附近采样会导致采样结果无界，积分转蒙特卡洛采样，方差可能会很大。重要性采样引入的提议分布p(x)会让被积函数有界。

2.2 重要性权重

首先知道函数 f(x) 在概率分布π(x)下的期望为

但这个期望的值无法直接得到，因此需要借助 p(x) 来进行采样，在p(x)上采用 {x1,x2,...,xn}后，可以估计f在分布p(x)下的期望为

对式子进行改写，即为

所以，可以得到

这个式子可以看作是定义在上的期望。

当在p(x)上采样 {x1,x2,...,xn} 后可以估计f的期望

这里就是重要性权重。

3 示例图代码

这里提供生成以上示例图的python代码。

3.1 蒙特卡洛积分估计示例

以下是使用均匀采样方法模拟积分过程的示例图代码。

import numpy as np
import matplotlib.pyplot as plt

# 定义二次函数形式
def quadratic_func(x, a, b, c):
    a = -0.5317
    b = 3.3944
    c = 14.4805
    return a * x**2 + b * x + c

# 生成平滑的曲线点
x_curve = np.linspace(-1, 10, 100)
y_curve = quadratic_func(x_curve, a, b, c)

# 创建图形
plt.figure(figsize=(10, 6))

# 绘制柱状图
_x_data = [0.1 + i*0.2 for i in range(0, 10)]
_y_data = [ quadratic_func(x, a, b, c)  for x in _x_data]
bars = plt.bar(_x_data, _y_data, width=0.1, alpha=0.7, color='skyblue', 
               edgecolor='navy', linewidth=1.2)

# 绘制拟合的二次曲线
plt.plot(x_curve, y_curve, 'r-', linewidth=2.5)

# 设置图形属性
plt.xlabel('X', fontsize=12)
plt.ylabel('Y', fontsize=12)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.xlim(0, 10)
plt.ylim(0, 28)

# 添加坐标轴刻度
plt.yticks(np.arange(0, 26, 5))

plt.tight_layout()
plt.show()

3.2 重要性采样图示例

以下是使用方形和圆形区域示例重要性采样的示例图代码。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches


# 定义二次函数形式
def quadratic_func(x, a, b, c):
    a = -0.5317
    b = 3.3944
    c = 14.4805
    return a * x**2 + b * x + c

# 生成平滑的曲线点
x_curve = np.linspace(-1, 10, 100)
y_curve = quadratic_func(x_curve, a, b, c)

# 创建图形
fig, ax = plt.subplots(1, 1, figsize=(10, 6))

# 绘制拟合的二次曲线
plt.plot(x_curve, y_curve, 'r-', linewidth=2.5)

# 添加圆形 (基于常见布局假设)
circle = patches.Circle((9.5, 3), 1, 
                       linewidth=2, edgecolor='red', 
                       facecolor='lightcoral')
ax.add_patch(circle)

# 添加长方形 (基于常见布局假设)
rectangle = patches.Rectangle((2, 5), 3, 15, linewidth=2, edgecolor='black', facecolor='lightblue')
ax.add_patch(rectangle)


# 设置图形属性
plt.xlabel('X', fontsize=12)
plt.ylabel('Y', fontsize=12)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.xlim(0, 10)
plt.ylim(0, 28)

# 添加坐标轴刻度
plt.yticks(np.arange(0, 26, 5))

plt.tight_layout()
plt.show()

3.3 重要性采样分布示例图

以下是重要性采样分布的示例图生成代码。

import matplotlib.pyplot as plt

# 创建图形
plt.figure(figsize=(8, 5))

# 绘制折线图 - 蓝色实线带圆点标记
y_values1 = [0, 0.2]
x_values1 = [0, 4]
plt.plot(x_values1, y_values1, 'green', linewidth=1.5, markersize=4)

# 绘制折线图 - 蓝色实线带圆点标记
y_values2 = [0.2, 0]
x_values2 = [4, 10]
plt.plot(x_values2, y_values2, 'yellow', linewidth=1.5, markersize=4)

# 设置坐标轴
plt.xlim(0, 10)
plt.ylim(0, 0.22)

# 设置网格（浅灰色虚线）
plt.grid(True, linestyle='--', color='gray', alpha=0.5)

# 设置刻度
plt.xticks(range(0, 10))
plt.yticks([i*0.02 for i in range(0, 11)])

# 精简样式，去掉边框
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)

plt.tight_layout()
plt.show()

reference

---

PPO算法逐行代码详解

https://zhuanlan.zhihu.com/p/660971357

重要性采样（Importance Sampling）

https://zhuanlan.zhihu.com/p/41217212

PPO优势函数的学习和解读

https://blog.csdn.net/liliang199/article/details/148875214

PPO在强化学习中的应用

https://blog.csdn.net/liliang199/article/details/148840758