本文还有配套的精品资源，点击获取

简介：快速傅里叶变换（FFT）是数字信号处理中的关键算法，特别在音频处理和语音识别中扮演着重要角色。本文将深入探讨FFT的基本概念、原理以及其在C语言中的实现，并结合国外专家的经验和实践进行详细讨论。FFT算法通过提高计算效率和降低DFT的复杂度，对于处理语音信号等长序列数据有显著优势。在C语言实现FFT的过程中，将涉及初始化、递归分治、蝶形运算、位反转和复数处理等关键步骤。此外，文章还讨论了如何将FFT应用于语音识别的后续分析，如计算功率谱密度和提取MFCC。"fft.rar"资源提供了FFT的C语言实现，是学习和实践音频处理技术的宝贵材料。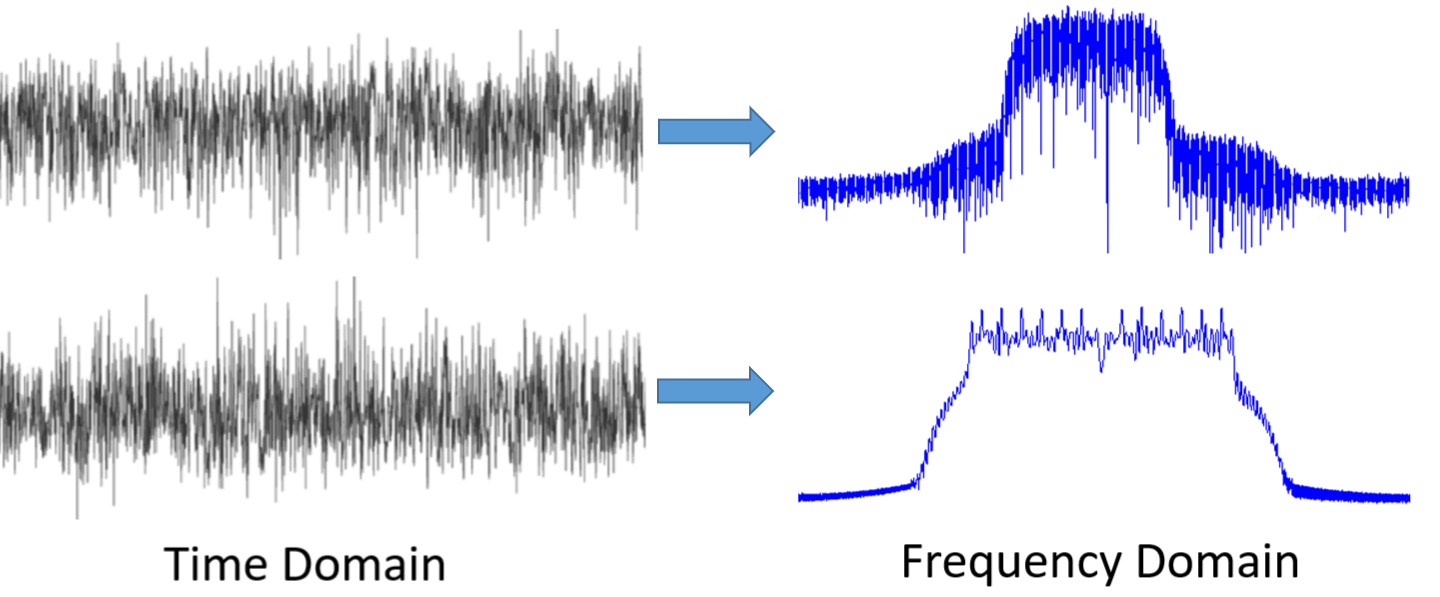

1. FFT的基本概念与原理

快速傅里叶变换（Fast Fourier Transform，FFT）是数字信号处理中的关键技术之一。它的出现极大提高了离散傅里叶变换（Discrete Fourier Transform，DFT）的计算速度，从而使得在计算机上处理复杂信号成为可能。FFT的核心在于减少计算的复杂度，从原始DFT的O(N^2)复杂度降至O(NlogN)，其中N为采样点数。这种效率的提升，使得FFT在音频分析、图像处理、语音识别等众多领域内得到了广泛应用。

傅里叶变换的历史和必要性

傅里叶变换的历史可以追溯到19世纪初，由法国数学家让-巴蒂斯特·约瑟夫·傅里叶提出。傅里叶变换允许我们分析信号的频域特性，从而对信号进行更深入的理解和处理。在工程领域，复杂信号往往可以通过其包含的不同频率的正弦波和余弦波的组合来表示。因此，将信号从时域转换到频域，进行分析和处理，然后再转换回时域，已经成为信号处理领域的常规操作。

基本原理和应用

在基本原理上，FFT允许我们将时域上的离散信号通过快速算法转换到频域。频域分析揭示了信号中不同频率成分的分布，对于信号的特征提取、噪声去除和压缩编码等操作至关重要。在实际应用中，FFT使得复杂的数字信号处理成为现实，并且降低了对计算资源的需求，推动了现代通信、图像和语音处理技术的发展。下一章我们将深入探讨FFT在音频处理中的具体应用案例。

2. FFT在音频处理中的应用

音频处理领域中，FFT技术的应用是无所不在的。它能够将音频信号从时域转换到频域，从而进行各种信号分析与处理。本章节将探讨FFT技术在音频信号分析与处理中的具体应用。

2.1 FFT音频信号分析

2.1.1 音频信号的频域分析

频域分析是对音频信号进行频谱分析的过程，其核心是将时域中的信号转换至频域中，以观察信号的频率组成。这在音乐、语音处理中极其重要，可以揭示音频信号的丰富特性，比如谐波、泛音列、谐音等。

音频信号的频域分析可以揭示信号的频率特性，这对于消除噪声、增强特定频率成分等操作至关重要。例如，在音乐制作中，通过频域分析能够识别出不需要的噪声或回声，并进行相应的处理。

以下是频域分析的一个简单示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft

# 生成音频信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)  # 时间向量
freq = 5  # 信号频率
signal = 0.6*np.sin(2 * np.pi * freq * t)  # 生成5Hz的正弦信号

# FFT变换
signal_fft = fft(signal)

# 频率向量
freqs = np.fft.fftfreq(t.shape[-1], 1/fs)

# 绘制频谱图
plt.figure(figsize=(12, 6))
plt.plot(freqs, np.abs(signal_fft))
plt.title('Frequency Spectrum of the Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()
plt.show()

2.1.2 音频信号的时域分析

虽然频域分析在音频处理中非常重要，但时域分析同样有其不可替代的作用。时域分析关注的是信号随时间变化的特性，这对于检测信号的瞬态变化、进行时间对齐和同步等任务非常有用。

例如，在检测录音开始的瞬间，或者分析声音的瞬态响应时，时域分析是最直观的方式。可以通过波形图展示信号随时间的变化，这有助于识别和处理音频的特定部分。

2.2 FFT音频信号处理

2.2.1 音频信号的滤波与去噪

滤波与去噪是音频处理中常见的任务，目的是从音频信号中去除不需要的噪声成分，同时保留或增强信号中的有用部分。FFT在这里的作用是将信号转换到频域，使得滤波操作变得容易实施。

以低通滤波为例，一旦在频域识别出高于特定频率的信号部分，就可以将这些部分置零或衰减，然后通过逆FFT将信号还原到时域，得到去噪后的音频信号。

2.2.2 音频信号的压缩与编码

音频压缩与编码是为了减少音频文件的存储空间或传输带宽，同时尽量保持音质。使用FFT将音频转换到频域后，可以利用人类听觉的特性来去除人耳难以察觉的频率成分，从而实现有损压缩。

例如，MP3编码算法就是一种使用了FFT技术的音频压缩方法。它通过量化频域中的信号，并只保留对人耳最重要的部分，达到压缩音频数据的目的。

总结

FFT在音频处理中的应用覆盖了从基本的信号分析到复杂的信号处理任务，它是音频工程不可或缺的工具。理解FFT的基本原理和应用方式，对于开发高效和高质量的音频处理系统至关重要。在下一章节中，我们将探讨FFT在语音识别领域的应用，分析其如何帮助改善语音识别的准确性与效率。

3. FFT在语音识别中的应用

3.1 语音信号的频谱特性分析

3.1.1 语音信号的频谱表示

语音信号本质上是一种模拟信号，它包含了丰富的频率成分。在语音识别过程中，将语音信号从时域转换到频域，可以更好地理解和处理信号。快速傅里叶变换（FFT）是将时域信号转换为频域信号的重要工具。频谱表示指的是将语音信号的时域波形通过FFT变换为频率的分布图，也就是频谱。

频谱图中，横轴代表频率，纵轴代表该频率分量的幅度。通过频谱图，我们可以直观地看到不同频率成分的强弱。这种分析对于理解语音信号的特性至关重要，尤其是对于语音识别系统来说，它能够帮助系统识别出语音信号中的关键特征。

3.1.2 语音信号的特征提取方法

语音信号的特征提取是从复杂的语音信号中提取出对识别任务有用的信息。常见的特征包括梅尔频率倒谱系数（MFCCs）、线性预测编码系数（LPCs）和谱包络等。这些特征能够有效捕捉到语音信号的关键信息，如音素的频谱特性。

提取特征的过程中，FFT扮演了至关重要的角色。首先，它能够快速将时域中的语音信号转换为频谱信号，然后，基于得到的频谱信号，可以进一步计算出所需的特征。在特征提取中，FFT不仅仅作为一个工具存在，它还是很多特征计算算法的底层支持。

3.2 FFT与语音识别技术的结合

3.2.1 FFT在语音特征提取中的作用

在语音识别系统中，FFT将连续的时域信号转换为离散的频域信号，这一过程极大地方便了后续的特征提取。比如，MFCC特征提取就需要在频域中完成，通过FFT获得的频谱信息再经过一系列的变换得到最终的MFCC系数。

使用FFT进行特征提取的主要步骤包括：首先进行窗口化处理，然后对每个窗口内的信号进行FFT变换得到频谱，接着通过梅尔滤波器组得到滤波后的能量，并通过取对数和离散余弦变换（DCT）计算MFCC系数。这一系列操作都是基于FFT对信号处理的高效性。

3.2.2 FFT与语音识别模型的融合策略

FFT与语音识别模型的融合需要考虑如何高效地结合两者以提升识别的准确性和速度。常见的语音识别模型包括隐马尔可夫模型（HMM）、深度神经网络（DNNs）和卷积神经网络（CNNs）等。

在融合FFT和这些模型时，关键是设计能够有效利用频谱特征的网络结构或算法。例如，在使用CNN对语音信号进行识别时，可以将FFT得到的频谱图作为输入，直接训练网络识别不同频谱图所代表的语音类别。此外，FFT还可以与时间递归神经网络（RNN）结合，用于提取动态特征，为模型提供时序信息。

3.2.3 FFT与现代语音识别系统的融合实例

在现代语音识别系统中，FFT已经被广泛使用。例如，Google的语音搜索应用中，FFT用于快速计算语音信号的频谱表示，这样可以在用户说出搜索词的同时，系统能够实时地提取特征并进行匹配。

另一个例子是苹果公司的Siri，它在接收用户的语音命令前，也会使用FFT分析语音信号，并将得到的特征送入深度学习模型进行进一步的处理。通过这种结合，FFT不仅提高了特征提取的效率，也提升了整个语音识别系统的性能。

通过上述章节的深入分析，我们可以看到FFT在语音识别中的重要性。它不仅为频谱分析提供了高效的计算方法，而且为语音特征提取和模型训练提供了丰富的信息。在后续章节中，我们将进一步探讨FFT在编程语言中的实现以及优化技巧。

4. FFT在C语言中的实现方法

4.1 C语言中的FFT基础实现

4.1.1 C语言环境准备与库的调用

在C语言中实现FFT，首先需要准备好开发环境，并引入必要的库。对于大多数操作系统，可以使用GCC编译器来编译C代码。此外，对于FFT算法的实现，我们通常会使用一些数学库，如GNU Scientific Library (GSL) 或者是专门为FFT优化的库，比如FFTW（Fastest Fourier Transform in the West）。以下示例将展示如何在C语言中设置开发环境，并调用一个FFT库。

假设使用的是FFTW库，可以通过以下步骤进行安装：

sudo apt-get install libfftw3-dev  # Debian/Ubuntu系统
sudo yum install fftw-devel        # CentOS/RHEL系统

然后在C代码中包含必要的头文件：

#include <fftw3.h>
#include <stdio.h>
#include <math.h>

int main() {
    // FFTW计划初始化和执行的代码将在这里
    return 0;
}

4.1.2 一维FFT的C语言实现

下面的代码段展示了如何用C语言实现一个简单的二维FFT。我们首先初始化输入数组，然后创建输出数组，接着创建一个计划来计算FFT，最后执行该计划并输出结果。

#define N 1024 // 设置变换点数为1024

int main() {
    fftw_complex *in, *out;
    fftw_plan p;

    // 分配输入输出数组
    in = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);

    // 初始化输入数组，这里假设简单地初始化为i
    for(int i = 0; i < N; ++i) {
        in[i][0] = i; // 实部
        in[i][1] = 0; // 虚部
    }

    // 创建计划并执行FFT
    p = fftw_plan_dft_1d(N, in, out, FFTW_FORWARD, FFTW_ESTIMATE);
    fftw_execute(p);

    // 打印输出结果
    for(int i = 0; i < N; ++i) {
        printf("%f + %fi\n", out[i][0], out[i][1]);
    }

    // 清理资源
    fftw_destroy_plan(p);
    fftw_free(in);
    fftw_free(out);

    return 0;
}

在这个简单的例子中，我们创建了一个指向复数数组的指针 in 和 out ，分别用于存储输入和输出数据。接着，我们使用 fftw_plan_dft_1d 函数创建了一个FFT计划，并指定了变换的方向（ FFTW_FORWARD ）和算法的估计方式（ FFTW_ESTIMATE ）。然后，我们通过 fftw_execute 函数执行该计划，并将结果打印到控制台。

在实际应用中，为了得到有意义的频谱信息，输入数据通常来自实际的信号采样。不过在此示例中，为简单起见，我们仅使用了简单的数字序列来模拟输入信号。

4.2 FFT实现中的优化策略

4.2.1 性能优化技巧

性能优化是FFT实现过程中非常重要的一环，特别是对于需要大量FFT运算的场景。优化FFT实现时，常见的技巧包括：

• 使用合适的FFT库：有些库为了可移植性牺牲了性能，而有些库则针对特定的硬件架构进行了优化。
• 避免不必要的数据复制：在处理数据时，尽量减少数据在内存中的复制操作，这样可以减少不必要的内存访问和CPU周期消耗。
• 利用缓存机制：确保频繁访问的数据被放在缓存中，可以大幅度提高数据访问的速度。

4.2.2 内存管理与优化

在FFT的实现中，正确的内存管理对于性能和程序稳定性都至关重要。关键点包括：

• 避免内存泄漏：确保所有分配的内存都被释放。
• 使用内存池：对于频繁分配和释放相同大小内存的情况，使用内存池可以避免碎片化，并提高内存分配速度。
• 内存对齐：确保数据结构在内存中对齐，以提高CPU对内存的访问速度。

4.2.3 代码示例与解析

下面的代码展示了如何在C语言中实现FFT，并对数据进行内存管理与优化。我们将关注内存分配、数据操作、以及最终释放资源的过程。

// FFTW计划初始化和执行的代码
// ...（此处省略了前面的初始化和数组填充代码）

// FFT执行与结果输出
fftw_execute(p);
for(int i = 0; i < N; ++i) {
    printf("%f + %fi\n", out[i][0], out[i][1]);
}

// FFT计划和数据的清理
fftw_destroy_plan(p);
fftw_free(in);
fftw_free(out);

在上述代码中，内存的分配是通过 fftw_malloc 完成的，并且需要确保执行 fftw_free 来释放内存。通过合理的内存管理，我们能够避免内存泄漏，并确保程序的长期稳定运行。

在数据操作方面，我们使用了FFTW库提供的 fftw_execute 函数来执行FFT计划，并将结果直接写入之前分配的输出数组中。这样的操作减少了不必要的数据复制，有助于提升整体性能。

通过这些实践，我们能够在C语言中高效地实现FFT，并对其性能进行优化。

5. FFT算法的关键步骤及高效库使用

5.1 FFT算法的关键步骤解析

快速傅里叶变换（FFT）算法通过将复杂的DFT问题分解成更小的子问题，然后使用递归或迭代方法解决这些子问题。这大大减少了计算量，使得FFT的复杂度由DFT的O(N^2)降低到O(NlogN)。

5.1.1 初始化过程

初始化阶段通常包括设置算法的起始参数，例如确定输入数据的长度N，通常是2的幂次方，因为FFT算法在这样的情况下最为高效。此外，初始化还涉及到分配必要的内存空间以及设置迭代或递归的基准情况。

5.1.2 递归分治过程

FFT算法使用分治法来简化计算。这涉及将原始的DFT问题分解成较小的DFT问题。在递归实现中，问题被不断分解直到达到基本情况。然后，问题通过合并子问题的解来解决。

5.1.3 蝶形运算和位反转

递归或迭代的FFT算法中，蝶形运算是一种重要的步骤，它结合了输入数据的元素以及旋转因子（twiddle factors）进行计算。这些旋转因子在不同的层面上是不同的，它们与旋转角度相关，通常表示为复数。位反转操作是指对数据点的索引进行重排，以确保在每个递归或迭代步骤中正确地配对和计算。

5.1.4 复数处理与结果输出

FFT算法处理的是复数输入和输出。输入数据被假定为时域复数序列，输出数据是频域中的复数表示。处理包括复数加法和乘法运算，而结果输出是复数数组，表示信号在不同频率下的幅度和相位。

5.2 高效FFT库的介绍与应用

在实际应用中，由于FFT算法的复杂性，开发者通常倾向于使用现成的、经过优化的FFT库来实现快速傅里叶变换。这些库封装了FFT算法的关键步骤，并提供了易于使用的接口。

5.2.1 FFTW库的使用方法

FFTW（Fastest Fourier Transform in the West）是最受欢迎的开源FFT库之一。它使用了复杂的代码生成技术，能够生成针对特定硬件优化的FFT代码。使用FFTW库的基本步骤通常包括： - 包含FFTW库头文件。 - 分配输入和输出数组。 - 创建FFT计划（plan）。 - 执行FFT变换。 - 清理资源。

5.2.2 其他常用FFT库的对比与选择

市场上存在多种FFT库，如KissFFT、Intel MKL、cuFFT（针对GPU加速）。每个库都有其独特的优势和使用场景。选择合适的库通常基于以下因素： - 性能需求。 - 平台兼容性（CPU、GPU、FPGA等）。 - 开发环境（如语言支持和API设计）。 - 社区支持和文档质量。 - 开源还是商业。

5.3 频谱分析在语音识别中的应用实例

FFT算法在语音识别领域中应用广泛，特别是在频谱分析和特征提取过程中。

5.3.1 功率谱密度的应用

功率谱密度（PSD）是语音信号频谱分析中一个非常重要的参数，它表示信号功率在频域中的分布。通过计算PSD，可以识别语音信号中的共振峰和谐波结构，这对于语音信号的特征提取至关重要。

5.3.2 MFCC特征提取与应用

梅尔频率倒谱系数（MFCC）是语音识别中常用的特征参数。它们通过以下步骤从信号中提取： - 对信号应用预加重滤波器。 - 将信号分帧并应用窗函数。 - 计算每一帧信号的FFT。 - 将频谱转换为梅尔刻度。 - 应用离散余弦变换（DCT）获取MFCC系数。

5.4 国外开发者在FFT应用上的经验和技巧分享

国际开发者社区在FFT算法的应用和优化上有着丰富的经验和独到的见解。

5.4.1 国外研究者的最佳实践

国外研究者通常分享在FFT应用中的最佳实践，例如： - 使用FFT库而不是从头开始编写FFT算法。 - 对FFT算法进行优化，例如使用SIMD指令集或并行计算。 - 适当地使用算法分支，比如在数据长度不是2的幂时。

5.4.2 开源社区的贡献与创新

开源社区是FFT算法创新和优化的主要推动力。贡献者们： - 不断改进现有的FFT库，修复bug，提高性能。 - 发布新的FFT库，采用最新算法和优化技术。 - 在论坛和会议上交流最新研究成果和应用案例。

在本章节中，我们深入探讨了FFT算法的核心步骤，高效库的使用以及如何将FFT技术应用于语音识别的频谱分析。这些内容为希望掌握FFT算法并在实际项目中应用的IT专业人员提供了宝贵的信息和实践经验。

本文还有配套的精品资源，点击获取

简介：快速傅里叶变换（FFT）是数字信号处理中的关键算法，特别在音频处理和语音识别中扮演着重要角色。本文将深入探讨FFT的基本概念、原理以及其在C语言中的实现，并结合国外专家的经验和实践进行详细讨论。FFT算法通过提高计算效率和降低DFT的复杂度，对于处理语音信号等长序列数据有显著优势。在C语言实现FFT的过程中，将涉及初始化、递归分治、蝶形运算、位反转和复数处理等关键步骤。此外，文章还讨论了如何将FFT应用于语音识别的后续分析，如计算功率谱密度和提取MFCC。"fft.rar"资源提供了FFT的C语言实现，是学习和实践音频处理技术的宝贵材料。

本文还有配套的精品资源，点击获取