DPO (Direct Preference Optimization) 学习笔记

十月十三日更新

一、 核心思想：为何需要 DPO？

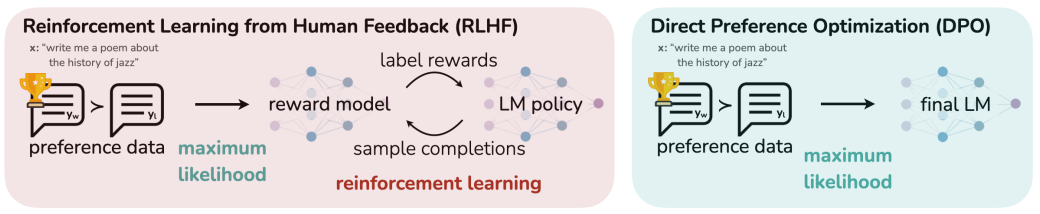
传统的基于人类反馈的强化学习（RLHF）通常是一个复杂的三阶段过程：

1. 监督微调 (SFT)：让模型具备基础能力。
2. 训练奖励模型 (Reward Model, RM)：用人类偏好数据（例如，回答A比回答B好）训练一个独立的模型，让它学会给回答打分。
3. 强化学习 (RL)：使用 PPO 等算法，让语言模型在奖励模型的指导下进行优化，以产生能获得更高分数的回答。

这个流程虽然有效，但存在一些问题：训练过程复杂、不稳定，且需要维护两个大型模型（语言模型和奖励模型）。奖励模型（RM）的准确性成为了整个流程的瓶颈，如果奖励模型的效果不佳，那么后续的所有强化学习阶段都会受此影响。

DPO 的核心思想 是一种范式转移：我们能否跳过显式训练奖励模型这一步，直接利用偏好数据来优化语言模型本身？

DPO 巧妙地证明了，我们可以通过一个简单的分类目标，直接优化语言模型，使其行为与人类偏好对齐。它将“拟合奖励模型”和“强化学习”这两个步骤合并成了一个等价的、更简单的损失函数。

二、 关键概念与定义

在推导之前，我们先明确几个关键定义：

• 策略 (Policy) $\pi$：指语言模型本身。我们希望优化的目标策略记为 ${\pi }_{\theta }$。
• 参考策略 (Reference Policy) ${\pi }_{ref}$：通常是经过 SFT 阶段的模型。它的作用是作为优化的起点和锚点，防止模型在优化过程中“能力退化”或偏离太远。
• 人类偏好数据：数据集中的每个样本包含一个问题（prompt）$x$，一个被人类偏爱的回答（winner）$y_w$，和一个不被偏爱的回答（loser）$y_l$。记为 $(x,y_w,y_l)$。
• 奖励函数 $r(x,y)$：一个未知的、潜在的函数，它能够根据人类的偏好给出一个分数。在传统 RLHF 中，我们需要拟合它；在 DPO 中，我们绕过它。

三、 DPO 公式推导：从 RLHF 目标到分类损失

DPO 的推导从 RLHF 的通用目标出发，通过一系列数学变换，最终得到了一个简单的分类损失函数。

第一步：从带约束的强化学习目标出发

在 RLHF 中，我们的优化目标是最大化奖励，同时不与参考策略 ${\pi }_{ref}$ 偏离太远。这个目标可以写成如下形式：

$$\underset{\pi }{\max }{E}_{x\sim D,y\sim \pi (y|x)}[r(x,y)]-\beta D_{KL}(\pi (y|x)||{\pi }_{ref}(y|x))$$

• $E[\cdot ]$ 项表示最大化期望奖励。
• $D_{KL}(\cdot )$ 项是 KL 散度，作为惩罚项，防止 $\pi$ 与 ${\pi }_{ref}$ 相差过大。$\beta$ 是控制惩罚强度的超参数。

可以证明，这个优化问题的最优解 ${\pi }^{\ast }(y|x)$ 具有以下形式：

$${\pi }^{\ast }(y|x)=\frac{1}{Z(x)}{\pi }_{ref}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$$

相关证明运用了拉格朗日乘子法和KKT约束条件，具体过程详见文末。

其中$Z(x)$ 是一个配分函数，用于确保所有可能回答 $y$ 的概率之和为1。它的具体形式是：
$$Z(x)=\sum _y{\pi }_{ref}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$$

这个公式非常关键，它建立了最优策略 ${\pi }^{\ast }$、参考策略 ${\pi }_{ref}$ 和潜在奖励函数 $r(x,y)$ 之间的桥梁。

第二步：反解奖励函数

既然我们知道了最优策略和参考策略的关系，我们可以反过来，从这个关系中解出奖励函数 $r(x,y)$。

对上面的最优策略公式稍作变换：
$$\exp \left(\frac{1}{\beta }r(x,y)\right)={\pi }^{\ast }(y|x)\cdot Z(x)\cdot \frac{1}{{\pi }_{ref}(y|x)}$$
两边取对数：
$$\frac{1}{\beta }r(x,y)=\log \left(\frac{{\pi }^{\ast }(y|x)}{{\pi }_{ref}(y|x)}\right)+\log Z(x)$$
最终得到：
$$r(x,y)=\beta \log \left(\frac{{\pi }^{\ast }(y|x)}{{\pi }_{ref}(y|x)}\right)+\beta \log Z(x)$$

这个公式告诉我们，任何语言模型策略（这里指最优策略 ${\pi }^{\ast }$）都可以被看作是相对于参考策略 ${\pi }_{ref}$ 的一个隐式奖励函数。奖励分数与两个策略对同一个回答的概率比值的对数成正比。

第三步：将奖励函数与人类偏好关联

现在，我们把人类偏好数据 $(x,y_w,y_l)$ 引入。我们假设人类的偏好符合 Bradley-Terry 模型。该模型指出，人类更偏爱 $y_w$ 而不是 $y_l$ 的概率 $P(y_w\succ y_l|x)$ 可以由它们各自的奖励分数差通过一个 logistic 函数来建模：

$$P(y_w\succ y_l|x)=\sigma (r(x,y_w)-r(x,y_l))$$

其中 $\sigma (z)=\frac{1}{1+e^{-z}}$ 是 logistic sigmoid 函数，

具体为什么使用这个公式见文章后。

现在，我们将第二步中反解出的奖励函数表达式代入上式：

$$r(x,y_w)-r(x,y_l)=\left[\beta \log \frac{{\pi }^{\ast }(y_w|x)}{{\pi }_{ref}(y_w|x)}+\beta \log Z(x)\right]-\left[\beta \log \frac{{\pi }^{\ast }(y_l|x)}{{\pi }_{ref}(y_l|x)}+\beta \log Z(x)\right]$$

代入后 配分函数 $\log Z(x)$ 在相减的过程中被完美地消掉了， 这极大地简化了问题。

$$r(x,y_w)-r(x,y_l)=\beta \left(\log \frac{{\pi }^{\ast }(y_w|x)}{{\pi }_{ref}(y_w|x)}-\log \frac{{\pi }^{\ast }(y_l|x)}{{\pi }_{ref}(y_l|x)}\right)$$

第四步：构建最终的 DPO 损失函数

我们的目标是让我们的模型 ${\pi }_{\theta }$ 尽可能地接近这个理论上的最优策略 ${\pi }^{\ast }$。所以，我们用 ${\pi }_{\theta }$ 来替换 ${\pi }^{\ast }$，然后最大化所有人类偏好数据的对数似然。

最大化 $P(y_w\succ y_l|x)$ 等价于最小化它的负对数似然：

$$L_{DPO}({\pi }_{\theta },{\pi }_{ref})=-E_{(x,y_w,y_l)\sim D}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }(y_w|x)}{{\pi }_{ref}(y_w|x)}-\beta \log \frac{{\pi }_{\theta }(y_l|x)}{{\pi }_{ref}(y_l|x)}\right)\right]$$

这就是最终 DPO 损失函数。我们来解读一下这个损失函数：

• 它是一个分类损失。形式上，它非常像一个二元交叉熵损失。
• $\log \frac{{\pi }_{\theta }(y_w|x)}{{\pi }_{ref}(y_w|x)}$：可以看作是我们的模型 ${\pi }_{\theta }$ 认为“更优回答” $y_w$ 相对于参考模型的“优势”或“改进幅度”。
• $\log \frac{{\pi }_{\theta }(y_l|x)}{{\pi }_{ref}(y_l|x)}$：同理，是模型认为“更差回答” $y_l$ 的“改进幅度”。
• 核心优化目标：为了最小化这个损失函数，模型必须最大化偏好回答 $y_w$ 的相对概率，同时最小化非偏好回答 $y_l$ 的相对概率。

通过优化这个简单的损失函数，我们间接地、但数学上等价地完成了传统 RLHF 中复杂的奖励建模和强化学习两个步骤。

---

四、详细公式推导

1. 最优策略 ${\pi }^{\ast }$ 公式推导

对于目标函数 $J(\pi )=E_{x\sim D,y\sim \pi (y|x)}[r(x,y)]-\beta D_{KL}(\pi (y|x)||{\pi }_{ref}(y|x))$，在其约束条件（$\pi$ 必须是一个有效的概率分布，即 ${\sum }_y\pi (y|x)=1$）下的最优解 ${\pi }^{\ast }$ 是什么。

推导方法：
这是一个在函数空间内寻找最优函数的问题，并且带有一个等式约束。解决这类问题的标准方法是拉格朗日乘子法。

为了简化，我们固定一个 prompt $x$，寻找最优的策略函数 $\pi (y|x)$。目标函数可以写为：
$$J(\pi )=\sum _y\pi (y|x)r(x,y)-\beta \sum _y\pi (y|x)\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}$$
约束条件是：$$\sum _y\pi (y|x)-1=0$$

步骤 1: 构建拉格朗日函数

我们将目标函数与约束条件结合，构建拉格朗日函数 $L(\pi ,\lambda )$：
$$L(\pi ,\lambda )=\left(\sum _y\pi (y|x)r(x,y)-\beta \sum _y\pi (y|x)\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}\right)-\lambda \left(\sum _y\pi (y|x)-1\right)$$
其中 $\lambda$ 是拉格朗日乘子。我们的目标是找到使 $L$ 取得极大值的 $\pi$。

步骤 2: 对 $\pi (y|x)$ 求偏导

为了找到极值点，我们将 $L$ 对每一个 $\pi (y|x)$ 求偏导，并令其等于 0。我们把 $\pi (y|x)$ 看作一个自变量。
$$\frac{\partial L}{\partial \pi (y|x)}=0$$

我们逐项进行求导：

• $\frac{\partial }{\partial \pi (y|x)}\left({\sum }_y\pi (y|x)r(x,y)\right)=r(x,y)$
• $\frac{\partial }{\partial \pi (y|x)}\left(-\beta {\sum }_y\pi (y|x)\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}\right)$: 这一项需要用到链式法则和乘法法则。
  • $\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}=\log \pi (y|x)-\log {\pi }_{ref}(y|x)$
  • $\frac{d}{dz}(z\log z)=\log z+1$
  • 所以，$\frac{\partial }{\partial \pi (y|x)}\left(-\beta \pi (y|x)(\log \pi (y|x)-\log {\pi }_{ref}(y|x))\right)=-\beta (\log \pi (y|x)-\log {\pi }_{ref}(y|x)+1)=-\beta \left(\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}+1\right)$
• $\frac{\partial }{\partial \pi (y|x)}\left(-\lambda ({\sum }_y\pi (y|x)-1)\right)=-\lambda$

将所有导数项合并，得到：
$$\frac{\partial L}{\partial \pi (y|x)}=r(x,y)-\beta \left(\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}+1\right)-\lambda =0$$

步骤 3: 求解 $\pi (y|x)$

现在我们从上式中解出 $\pi (y|x)$：
$$r(x,y)-\beta -\lambda =\beta \log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}$$$$\frac{r(x,y)-\beta -\lambda }{\beta }=\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}$$$$\frac{1}{\beta }r(x,y)-1-\frac{\lambda }{\beta }=\log \frac{\pi (y|x)}{{\pi }_{ref}(y|x)}$$

两边同时取指数：
$$\exp \left(\frac{1}{\beta }r(x,y)-1-\frac{\lambda }{\beta }\right)=\frac{\pi (y|x)}{{\pi }_{ref}(y|x)}$$
$$\pi (y|x)={\pi }_{ref}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)\exp \left(-1-\frac{\lambda }{\beta }\right)$$

步骤 4: 利用约束条件确定常数项

观察上式，$\exp \left(-1-\frac{\lambda }{\beta }\right)$ 这一项是一个与 $y$ 无关的常数（因为 $\lambda$ 是一个常数）。这个常数的作用就是进行归一化，以满足我们的约束条件 ${\sum }_y\pi (y|x)=1$。

我们将这个常数项记为 $1/Z(x)$，这里的 $Z(x)$ 就是配分函数。它只与 $x$ 有关，因为 $\lambda$ 是为固定的 $x$ 而计算的。
所以，最优策略 ${\pi }^{\ast }(y|x)$ 的形式就是：
$${\pi }^{\ast }(y|x)=\frac{1}{Z(x)}{\pi }_{ref}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$$
其中 $Z(x)={\sum }_y{\pi }_{ref}(y|x)\exp \left(\frac{1}{\beta }r(x,y)\right)$，以确保 ${\sum }_y{\pi }^{\ast }(y|x)=1$。

---

2. Bradley-Terry 模型与 Logistic Sigmoid 函数的推导

为什么人类对两个选项的偏好概率，可以用它们潜在奖励分数的差值，通过 logistic sigmoid 函数来建模？即 $P(y_w\succ y_l|x)=\sigma (r(x,y_w)-r(x,y_l))$ 是如何得出的。

这个模型的得出并非凭空捏造，它源于选择理论中的一个基本公理，并有一种非常直观和自然的推导方式。

推导方法：基于 Luce’s Choice Axiom

Luce’s Choice Axiom (卢斯选择公理) 是描述理性选择行为的一个基本原则。对于一个包含多个选项的集合，选择其中任一选项的概率，正比于该选项的“价值”或“强度”。

步骤 1: 定义价值/强度

假设每一个回答 $y$ 都有一个潜在的、不可观测的、正数“价值”评分，我们记为 $v(y)$。这个 $v(y)$ 直接关联到我们所说的奖励 $r(x,y)$。一个非常自然且常用的关联方式是指数关系：
$$v(y)=\exp (r(x,y))$$
选择指数关系有两个好处：

1. 保证价值为正：无论奖励 $r$ 是正还是负，其指数 $\exp (r)$ 永远是正数，符合价值的定义。
2. 数学性质良好：指数和对数运算在后续推导中非常方便。

步骤 2: 应用 Luce’s Choice Axiom

根据卢斯选择公理，在两个选项 $y_w$ 和 $y_l$ 中，选择 $y_w$ 的概率等于 $y_w$ 的价值占两者总价值的比例：
$$P(y_w\succ y_l|x)=\frac{v(y_w)}{v(y_w)+v(y_l)}$$

步骤 3: 代入指数价值并化简

现在，我们将 $v(y)=\exp (r(x,y))$ 代入上式：
$$P(y_w\succ y_l|x)=\frac{\exp (r(x,y_w))}{\exp (r(x,y_w))+\exp (r(x,y_l))}$$

为了得到我们熟悉的形式，我们对这个分式的分子和分母同时除以分子本身，即 $\exp (r(x,y_w))$：
$$P(y_w\succ y_l|x)=\frac{\frac{\exp (r(x,y_w))}{\exp (r(x,y_w))}}{\frac{\exp (r(x,y_w))}{\exp (r(x,y_w))}+\frac{\exp (r(x,y_l))}{\exp (r(x,y_w))}}=\frac{1}{1+\exp (r(x,y_l)-r(x,y_w))}$$

步骤 4: 关联 Logistic Sigmoid 函数

我们知道 logistic sigmoid 函数的定义是 $\sigma (z)=\frac{1}{1+e^{-z}}$。
观察上一步的结果，我们可以做一个简单的变换：
$$r(x,y_l)-r(x,y_w)=-(r(x,y_w)-r(x,y_l))$$所以，$$P(y_w\succ y_l|x)=\frac{1}{1+\exp (-(r(x,y_w)-r(x,y_l)))}$$
令 $z=r(x,y_w)-r(x,y_l)$，上式就变成了：$$P(y_w\succ y_l|x)=\frac{1}{1+e^{-z}}=\sigma (z)=\sigma (r(x,y_w)-r(x,y_l))$$