引入：(可跳过直接看后面的完整过程）

ps:为达到深入可视化，我在举例子处进行了更新（各位可以直接看例子，再来看具体理论）

1. 矩阵的列视角定义

在神经网络矩阵运算中，我们通常遵循以下约定：

• 矩阵的列（Columns）：表示输入特征维度

• 矩阵的行（Rows）：表示输出特征维度

例如，一个权重矩阵 W∈Rm×n：

• 左列（第一列）：对应第一个输入特征的权重

• 上列（第一行）：对应第一个输出特征的权重计算

---

2. LSTM核心矩阵的列结构

2.1 输入到隐藏层的权重矩阵 W∗​

以遗忘门的权重矩阵 WfWf​ 为例：

• 维度：Wf​∈R (h×d)

  • h：hidden_size（行数，输出维度）

  • d：input_size（列数，输入维度）

• 列视角：

  • 每一列对应输入的一个特征（如词向量的某一维）

  • 第k列：Wf​[:,k] 是输入第k个特征对所有隐藏层神经元的权重

# 示例：输入维度d=3，隐藏层h=2
W_f = [[w11, w12, w13],  # 上列：输出h1的权重
       [w21, w22, w23]]  # 下行：输出h2的权重
# 左列[w11, w21]：输入x1对h1,h2的权重

2.2 隐藏层到隐藏层的权重矩阵 U∗

以输入门的 Ui​ 为例：

• 维度：Ui​∈R (h×h)

• 列视角：

  • 每一列对应前一时刻隐藏状态的一个神经元

  • 第k列：Ui​[:,k] 是前一时刻第k个隐藏神经元对当前所有隐藏神经元的影响

---

3. 参数与矩阵维度的对应关系

3.1 单层LSTM的矩阵布局

对于单层LSTM，所有门（遗忘门、输入门、输出门、候选记忆）的权重矩阵会被纵向拼接：

W = [W_f; W_i; W_o; W_c]  # 维度 (4h × d)
U = [U_f; U_i; U_o; U_c]  # 维度 (4h × h)

• 列数：

  • W 的列数 = input_size（输入特征维度）

  • U 的列数 = hidden_size（隐藏层维度）

• 行数：4×hidden_size（因为4个门）

3.2 多层LSTM的堆叠

对于num_layers > 1的多层LSTM：

• 第k层的输入：

  • 第1层的输入：原始输入 xt​（维度 input_size）

  • 第k层（k≥2）的输入：前一层的隐藏状态 htk−1​（维度 hidden_size）

• 权重矩阵的调整：

  • 第1层的 W 维度：(4h×d)

  • 第k层的 W 维度：(4h×h)（因为输入来自前一层的隐藏状态）

---

4. 矩阵运算的跟踪示例

4.1 输入和隐藏状态的拼接

LSTM的实际计算会将输入 xt 和前一隐藏状态 ht−1​ 横向拼接：

z = [x_t; h_{t-1}]  # 维度 (d + h) × 1

此时：

• 矩阵左列：对应输入 xt​ 的特征

• 矩阵右列：对应隐藏状态 ht−1​ 的神经元

4.2 合并权重矩阵的列视角

将 W 和 U 横向拼接得到大矩阵 W=[W U]     维度 4h×(d+h）：

• 左半部分列（前d列）：处理输入的权重

• 右半部分列（后h列）：处理隐藏状态的权重

# 示例：h=2, d=3
W = [[w11, w12, w13 | u11, u12],  # 遗忘门（上列）
     [w21, w22, w23 | u21, u22],  # 遗忘门（下行）
     [..., ..., ... | ..., ...],   # 其他门...
     ...]

4.3 分块计算的门控信号

通过矩阵乘法 W⋅z 得到4个门的信号：

gates = W_f x_t + U_f h_{t-1}  # 遗忘门部分
       = W_f[:, :d] @ x_t + W_f[:, d:] @ h_{t-1}  # 列分块乘法

---

5. 代码实现与列视角验证

以下代码验证矩阵的列布局：

import numpy as np

input_size = 3
hidden_size = 2
num_layers = 2

# 单层LSTM的权重初始化
W = np.random.randn(4 * hidden_size, input_size + hidden_size)
print("W的维度:", W.shape)  # (8, 5)

# 列分块验证
W_input = W[:, :input_size]    # 处理输入的列 (8 × 3)
W_hidden = W[:, input_size:]   # 处理隐藏状态的列 (8 × 2)
assert W_input.shape == (4*hidden_size, input_size)
assert W_hidden.shape == (4*hidden_size, hidden_size)

---

6. 关键总结

参数	矩阵列意义	维度关系
input_size	W 的左半部分列数	输入特征维度
hidden_size	U 的列数或 W 的右半列数	隐藏神经元数量
num_layers	每层的 W 列数可能变化	第1层用input_size，之后用hidden_size

核心规则：

1. 左列永远对应输入特征（无论是原始输入还是前一层的隐藏状态）

2. 上列对应输出门控信号（如遗忘门、输入门等）

3. 多层LSTM中，第k≥2层的输入维度=hidden_size，因此其 W 的列数会减少。

 ——————————————————————————————————————————

完整过程

 ——————————————————————————————————————————

确标注所有维度变化和权重矩阵的拼接逻辑。

---

1. 输入与初始状态定义

• 输入向量：xt​∈R d×1 （d = input_size）

• 前一隐藏状态：ht−1​∈R h×1 （h = hidden_size）

• 前一记忆单元：ct−1​∈R h×1

---

2. 拼接输入与隐藏状态

zt​=[xt​ ht−1​​]∈R(d+h)×1

维度变化：

• xt​: (d×1)

• ht−1​: (h×1)

• 拼接后 zt​: (d+h)×1

• 

---

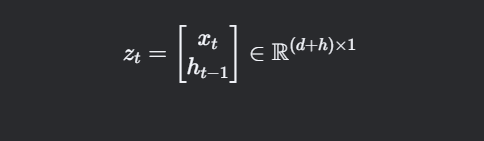
3. 权重矩阵的分块结构

每个门（遗忘门 f、输入门 i、输出门 o、候选记忆 c~）的权重矩阵 W∗​ 均分为两部分：

W∗=[W∗,input⏟d列 W∗,hidden⏟h列]∈R h×(d+h)

• 左半 W∗,input∈R h×d：处理输入 xt

• 右半 W∗,hidden∈R h×h：处理隐藏状态 ht−1

---

4. 分步计算各门信号

(1) 遗忘门 ft

ft=σ(Wf,inputxt⏟输入贡献+Wf,hidden ht−1⏟隐藏贡献+bf)∈R h×1

• 计算步骤：

  1. Wf,input​xt​: (h×d)⋅(d×1)→(h×1)(h×d)⋅(d×1)→(h×1)

  2. Wf,hidden​ht−1​: (h×h)⋅(h×1)→(h×1)(h×h)⋅(h×1)→(h×1)

  3. 相加后通过Sigmoid：(h×1)

(2) 输入门 it​ 和候选记忆 c~t

it=σ(Wi,input xt+Wi,hidden ht−1+bi)∈R h×1   

c~t=tanh⁡(Wc,input xt+Wc,hidden ht−1+bc)∈R h×1

• 维度变化：与遗忘门完全相同，仅权重和激活函数不同。

(3) 输出门 otot​

ot=σ(Wo,input xt+Wo,hidden ht−1+bo)∈R h×1

---

5. 合并计算的实现方式

实际代码中，所有门的计算会合并为一个矩阵乘法：

gates=W *zt+b∈R 4h×1,其中 W=[Wf Wi Wo Wc]∈R 4h×(d+h)

• 分块后的 W：

• 输出分割：

  gates=[ft it ot c~t],每部分 h×1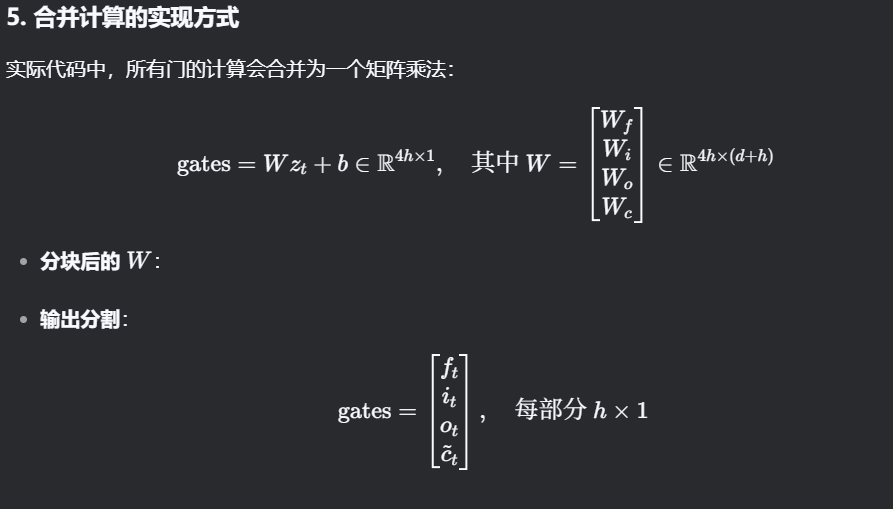

---

6. 记忆与隐藏状态更新

ct=ft ⊙ ct−1+it⊙c~t∈R h×1

ht=ot⊙tanh⁡(ct)∈R h×1

• 维度不变：所有操作保持 h×1。

---

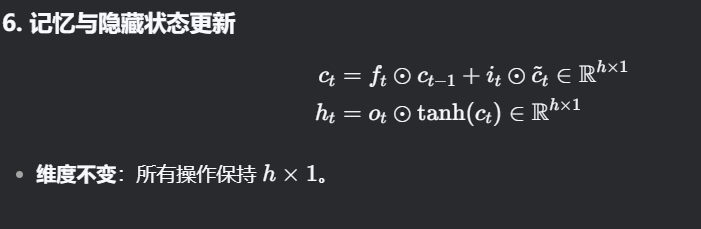
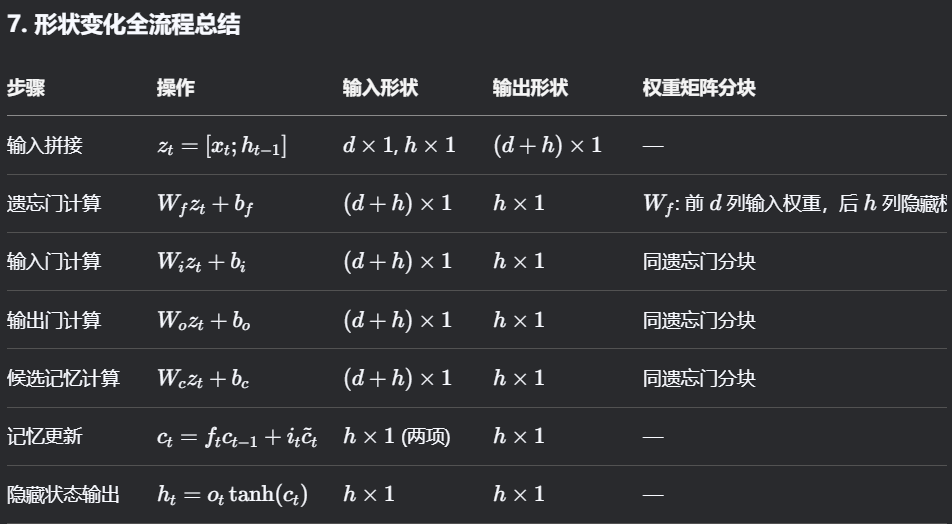
7. 形状变化全流程总结

---

8. 举例子

• 示例维度：假设 d=3（输入维度），h=2（隐藏层维度），则 W∈R 4h×(d+h)=R 8×5。

• 分块说明：

  • 前3列（蓝色/绿色/红色/紫色左半）：对应各门的输入权重 W∗,input​（处理 xt​）。

  • 后2列（蓝色/绿色/红色/紫色右半）：对应各门的隐藏权重 W∗,hidden​（处理 ht−1​）。

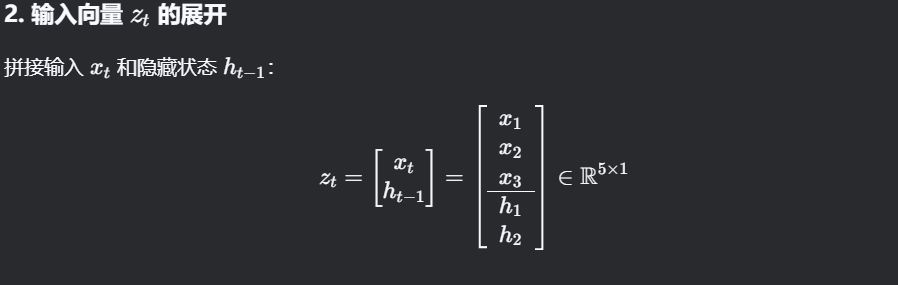
3. 矩阵乘法 Wzt​ 的逐步计算： gates=W* zt​ + b

 

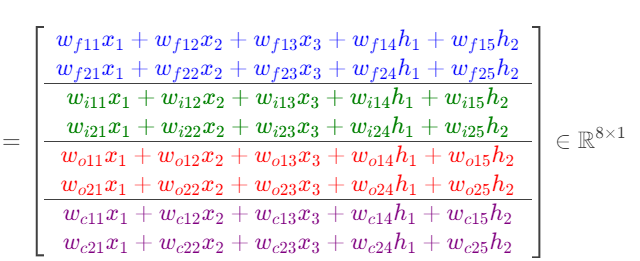
4. 分块提取各门信号 ：

 注意还要加上各自的偏置b!! gates=Wzt​+b

5.激活函数应用与状态更新(对照上图表）

门信号	计算式	输出形状
遗忘门 ft	σ(ft)	2×1
输入门 it	σ(it)	2×1
输出门 ot	σ(ot)	2×1
候选记忆 c~t	tanh⁡(c~t)	2×1

最终状态更新：

ct = ft ⊙ct−1+it⊙c~t ∈R 2×1

ht = ot ⊙tanh⁡(ct) ∈R 2×1

---

6. 代码验证分块计算

import torch

# 参数设置
d, h = 3, 2
W = torch.randn(4*h, d+h)  # (8, 5)
b = torch.randn(4*h, 1)    # (8, 1)
x_t = torch.randn(d, 1)    # (3, 1)
h_prev = torch.randn(h, 1) # (2, 1)
c_prev = torch.randn(h, 1) # (2, 1)

# 拼接输入
z_t = torch.cat([x_t, h_prev], dim=0)  # (5, 1)

# 矩阵乘法
gates = W @ z_t + b  # (8, 1)

# 分块提取各门
f_t = torch.sigmoid(gates[0:h])      # 遗忘门 (2, 1)
i_t = torch.sigmoid(gates[h:2*h])    # 输入门 (2, 1)
o_t = torch.sigmoid(gates[2*h:3*h])  # 输出门 (2, 1)
c̃_t = torch.tanh(gates[3*h:4*h])     # 候选记忆 (2, 1)

# 更新状态
c_t = f_t * c_prev + i_t * c̃_t
h_t = o_t * torch.tanh(c_t)