基于CasADi工具箱的模型预测控制求解示例学习，适合入门MPC轨迹跟踪运动控制器设计。 带录制视频讲解与配套MATLAB，python脚本文件，讲义文件等。 将MPC转换为非线性规划（NLP）问题的求解，并基于多重打靶法Multiple shooting将模型预测控制问题（MPC）转化为一般的NLP问题，进而利用CasADi工具箱对优化问题求解。 1.控制模型离散化 利用欧拉公式或其他数值离散化方法，采用一定间隔的离散时间，对连续模型离散化。 2.优化问题转化 将MPC优化问题转化为NLP问题。 MPC的最优控制（OCP）的表达形式如下所示： 3.利用CasADi，完成对NLP问题的求解。

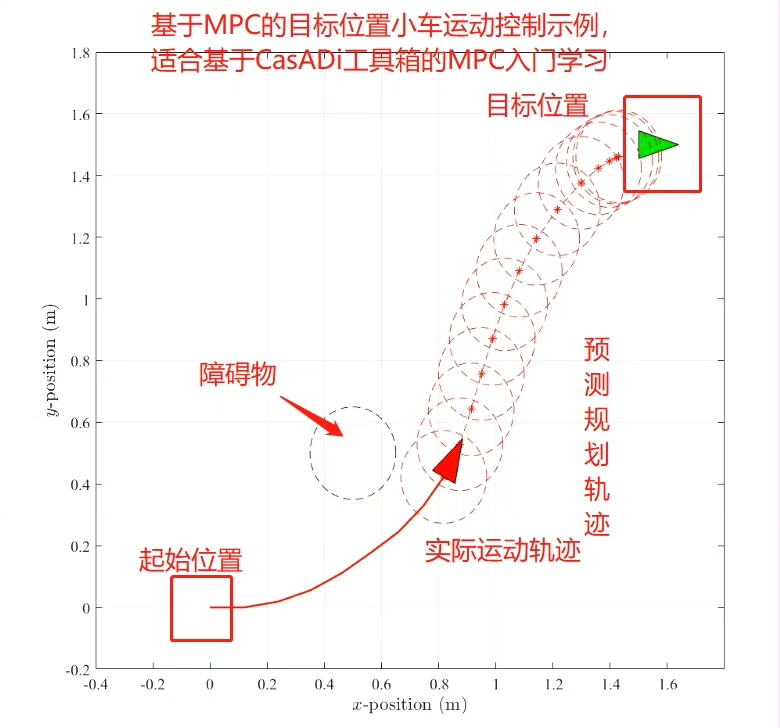
在自动驾驶和机器人等众多领域，模型预测控制（MPC）凭借其出色的性能，成为设计轨迹跟踪运动控制器的热门选择。今天就来和大家分享基于CasADi工具箱的MPC轨迹跟踪运动控制器设计示例学习，这个过程中还贴心准备了录制视频讲解，以及配套的MATLAB、Python脚本文件和讲义文件，非常适合入门。

MPC到NLP的转变

MPC本质上是求解一个最优控制问题（OCP），但为了方便求解，我们通常把它转化为非线性规划（NLP）问题。这里用到了多重打靶法（Multiple shooting），这种方法将模型预测控制问题（MPC）转化为一般的NLP问题，然后借助CasADi工具箱就能轻松求解优化问题啦。

控制模型离散化

实际应用中，我们的系统大多是连续的，但计算机处理需要离散的数据，所以要对连续模型离散化。常用的方法比如欧拉公式，当然也可以用其他数值离散化方法。

以一个简单的一阶系统 $\dot{x} = -ax + bu$ 为例，采用欧拉向前离散化，离散时间间隔设为 $T_s$。

连续状态方程为：

\[ \dot{x}(t) = -ax(t) + bu(t) \]

离散化后：

\[ x{k + 1} = xk + Ts(-axk + bu_k) \]

用Python代码简单示意离散化过程：

import numpy as np

# 定义参数
a = 1.0
b = 1.0
Ts = 0.1  # 离散时间间隔

# 初始状态
x_k = 0.0
u_k = 1.0

# 离散化更新状态
x_k_plus_1 = x_k + Ts * (-a * x_k + b * u_k)
print("离散化后的状态 x_{k+1}:", x_k_plus_1)

这里就是根据欧拉公式实现了简单的离散化，每次按照固定的时间间隔 Ts 更新系统状态。

优化问题转化

MPC的最优控制（OCP）有其特定的表达形式。一般来说，OCP要最小化一个代价函数，同时满足一系列约束条件。把MPC优化问题转化为NLP问题，核心就是将这些代价函数和约束用NLP能处理的形式表达出来。

假设MPC的代价函数为：

\[ J = \sum{k = 0}^{N - 1} (xk - x{ref,k})^2 + \rho uk^2 \]

其中，$x_{ref,k}$ 是参考状态，$\rho$ 是控制输入惩罚因子，$N$ 是预测时域。

状态转移方程作为约束：

\[ x{k + 1} = f(xk, u_k) \]

这样就把MPC的OCP转化为了NLP问题的形式，CasADi工具箱就可以大展身手啦。

利用CasADi求解NLP问题

CasADi是一个用于数值计算和优化的开源软件包，功能十分强大。下面用MATLAB代码示例如何利用CasADi求解转化后的NLP问题。

% 导入CasADi相关函数
import casadi.*

% 定义参数
N = 10; % 预测时域
rho = 0.1; % 控制输入惩罚因子
Ts = 0.1; % 离散时间间隔

% 定义状态和控制变量
x = SX.sym('x', 1); % 状态变量
u = SX.sym('u', 1); % 控制变量

% 定义状态转移函数
f = @(x, u) x + Ts * (-x + u);

% 定义代价函数
J = 0;
x_k = x;
for k = 1:N
    J = J + (x_k - 1)^2 + rho * u^2; % 参考状态设为1
    x_k = f(x_k, u);
end

% 定义优化变量
opt_variables = [x; repmat(u, N, 1)];

% 定义约束
g = [];
x_k = x;
for k = 1:N
    g = [g; x_k - f(x_k, u)];
    x_k = f(x_k, u);
end

% 定义优化问题
prob = struct('f', J, 'x', opt_variables, 'g', g);

% 选择求解器
solver = nlpsol('solver', 'ipopt', prob);

% 初始猜测值
x0 = [0; repmat(0, N, 1)];

% 求解
sol = solver('x0', x0);

在这段代码里，我们先定义了参数、状态和控制变量，构建了状态转移函数和代价函数。然后把优化变量和约束整合起来定义优化问题，选择 ipopt 求解器求解。通过这样的步骤，就利用CasADi完成了NLP问题的求解，进而实现MPC轨迹跟踪。

总之，通过控制模型离散化、优化问题转化以及CasADi求解这一系列步骤，我们就能实现基于CasADi工具箱的MPC轨迹跟踪运动控制器设计，希望大家能在这个过程中顺利入门MPC设计。配合我们提供的视频、脚本和讲义，相信学习效果会更好哦！