顶刊TAC 多智能体分布式自适应一致性控制（线性和非线性动力学，包含一个是纯一致性的 一个是leader-follower一致性的） 包含：文献+纯一致性 matlab 复现代码+leader-follower 一致性 matlab 复现代码 主要内容：本技术概要考虑具有一般线性和Lipschitz非线性动力学的多智能体系统的分布式一致性问题。 针对线性和非线性两种情况，设计了具有自适应调节相邻智能体间耦合权值的分布式相对状态一致性协议，使所有无向连通通信图都能达成一致性。 进一步研究了领导-追随者沟通图的推广情况。 与文献中的现有结果相反，这里的自适应一致性协议可以由每个智能体以完全分布式的方式实现，而不使用任何全局信息。

在多智能体系统的研究领域，顶刊TAC上关于多智能体分布式自适应一致性控制的研究成果相当瞩目，尤其是针对具有一般线性和Lipschitz非线性动力学的系统。

一、文献概述

此研究聚焦于多智能体系统的分布式一致性问题，在面对线性和非线性动力学场景时，设计出能自适应调节相邻智能体间耦合权值的分布式相对状态一致性协议，确保在所有无向连通通信图的情况下都能实现一致性。不仅如此，还对领导 - 追随者沟通图的推广情形展开了深入探究。与以往文献结果不同的是，这里提出的自适应一致性协议可让每个智能体以完全分布式的方式执行，无需借助任何全局信息。这一特性大大提升了多智能体系统在实际应用中的灵活性和自主性。

二、纯一致性Matlab复现代码及分析

% 纯一致性Matlab代码示例
% 定义智能体数量
n = 5; 
% 生成随机无向连通图
A = gallery('wgraph',n,1); 
% 拉普拉斯矩阵计算
L = diag(sum(A)) - A; 

% 初始状态
x0 = randn(n,1); 
% 时间设置
tspan = 0:0.01:10; 

% 定义动力学方程
odefun = @(t,x) -L*x; 

% 求解ODE
[t,x] = ode45(odefun,tspan,x0); 

% 绘图
figure;
for i = 1:n
    plot(t,x(:,i));
    hold on;
end
xlabel('时间 t');
ylabel('智能体状态');
title('纯一致性智能体状态随时间变化');
legend(strcat('智能体',num2str((1:n)')));

代码分析

1. 智能体数量与图生成：首先定义了智能体的数量 n，这里设置为5。然后通过 gallery('wgraph',n,1) 函数生成一个随机的无向连通图，并存储在邻接矩阵 A 中。无向连通图是确保智能体之间能够相互通信并达成一致性的基础结构。
2. 拉普拉斯矩阵计算：根据邻接矩阵 A 计算拉普拉斯矩阵 L，拉普拉斯矩阵在多智能体一致性研究中起着关键作用，它反映了智能体之间的连接关系以及信息传播的方式。
3. 初始状态与时间设置：随机生成智能体的初始状态 x0，这模拟了实际场景中智能体初始状态的不确定性。同时设置时间范围 tspan，用于观察智能体状态随时间的变化。
4. 动力学方程定义：定义 odefun 函数来描述智能体的动力学方程，这里是 -L*x，表明每个智能体的状态变化率与拉普拉斯矩阵和自身状态相关，这正是实现一致性的核心规则。
5. 求解与绘图：使用 ode45 函数求解常微分方程，得到每个时间点上智能体的状态。最后通过绘图直观展示每个智能体状态随时间的变化过程，从图中可以观察到智能体状态逐渐趋于一致。

三、Leader - Follower一致性Matlab复现代码及分析

% Leader - Follower一致性Matlab代码示例
% 智能体数量
n = 5; 
% 领导者索引
leader = 1; 
% 生成随机无向连通图（包含领导者与追随者连接）
A = gallery('wgraph',n,1); 
% 假设领导者与其他智能体有连接（这里简单处理，实际可能更复杂）
A(leader,:) = 1; A(:,leader) = 1; A(leader,leader) = 0; 
% 拉普拉斯矩阵计算
L = diag(sum(A)) - A; 

% 初始状态
x0 = randn(n,1); 
% 时间设置
tspan = 0:0.01:10; 

% 定义动力学方程（考虑领导者 - 追随者）
odefun = @(t,x) -L*x; 
if leader ~= 1
    odefun = @(t,x) [-x(leader); -L(2:end,2:end)*(x(2:end)-x(leader)*ones(n - 1,1))];
end

% 求解ODE
[t,x] = ode45(odefun,tspan,x0); 

% 绘图
figure;
for i = 1:n
    plot(t,x(:,i));
    hold on;
end
xlabel('时间 t');
ylabel('智能体状态');
title('Leader - Follower一致性智能体状态随时间变化');
legend(strcat('智能体',num2str((1:n)')));

代码分析

1. 领导者设定与图调整：在代码开头除了定义智能体数量 n 外，还指定了领导者的索引 leader。生成无向连通图后，通过一些操作确保领导者与其他追随者之间有连接，这里简单地将领导者与所有智能体建立连接（实际场景可能需更细致的连接设计）。
2. 拉普拉斯矩阵重新计算：基于调整后的邻接矩阵 A 重新计算拉普拉斯矩阵 L，因为图结构的改变会影响智能体间信息传播的方式，拉普拉斯矩阵也相应改变。
3. 动力学方程调整：根据是否是领导者来定义不同的动力学方程 odefun。如果当前智能体不是领导者，动力学方程会考虑与领导者状态的差异，使追随者朝着领导者的状态调整，这体现了领导者 - 追随者一致性的核心机制。
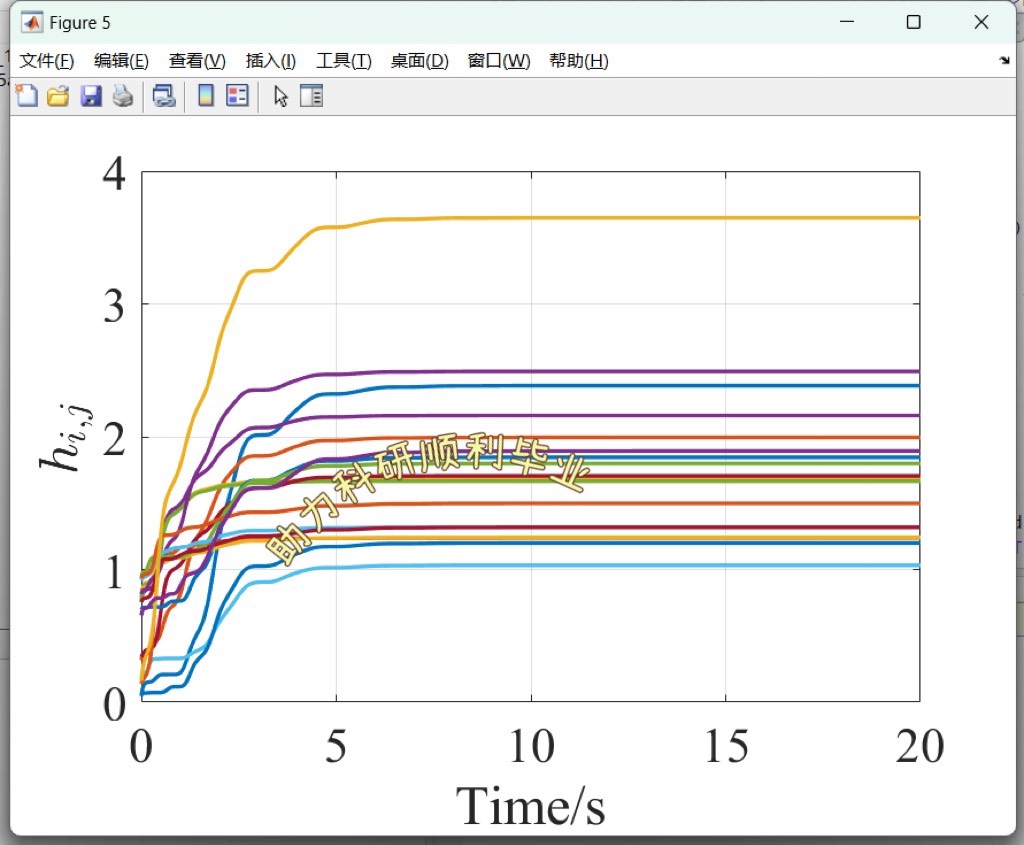
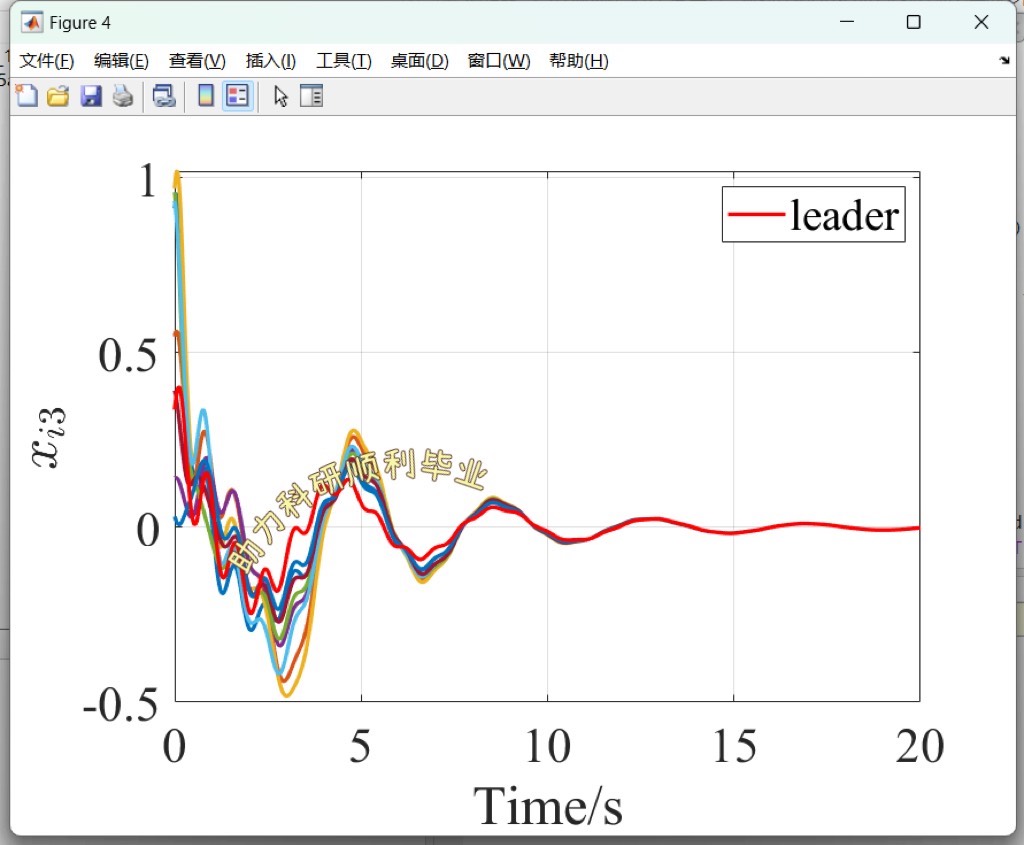
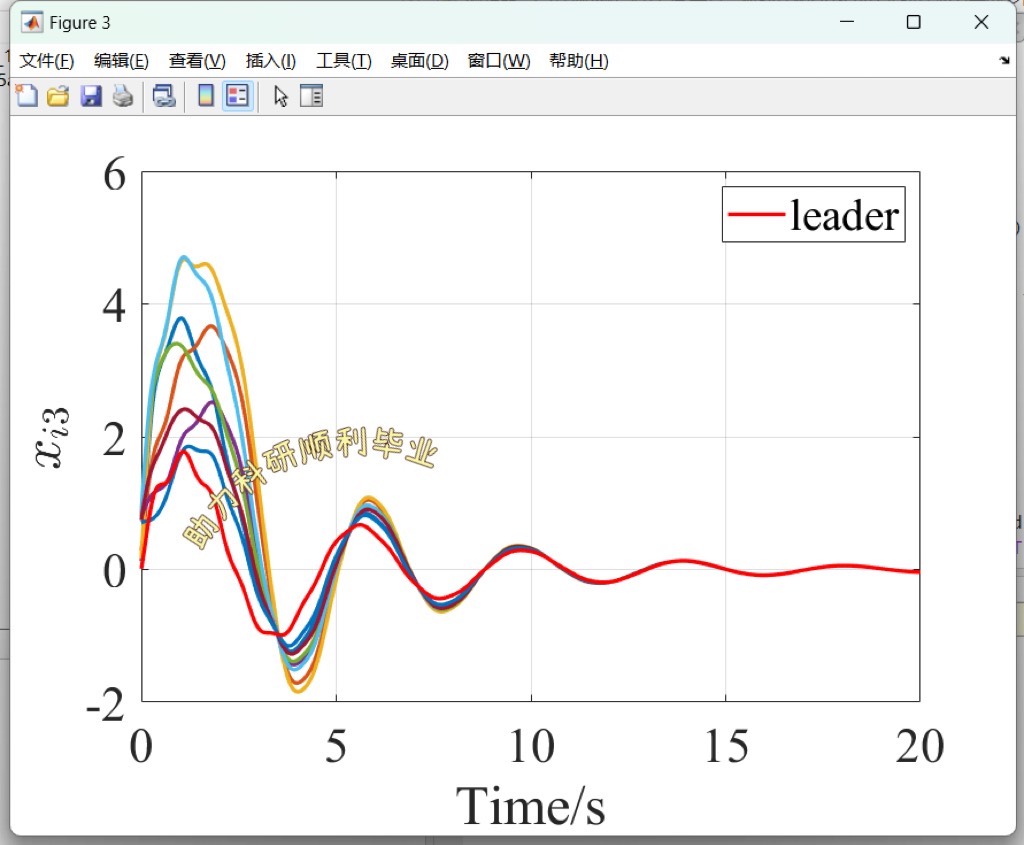
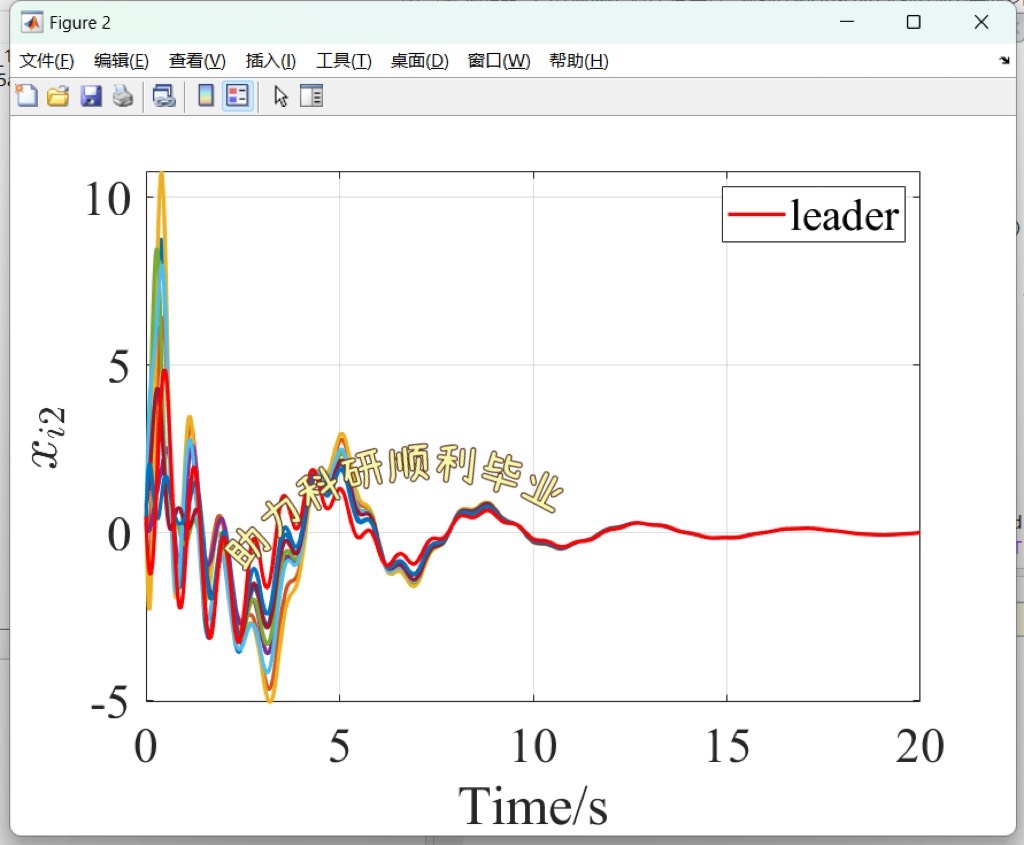
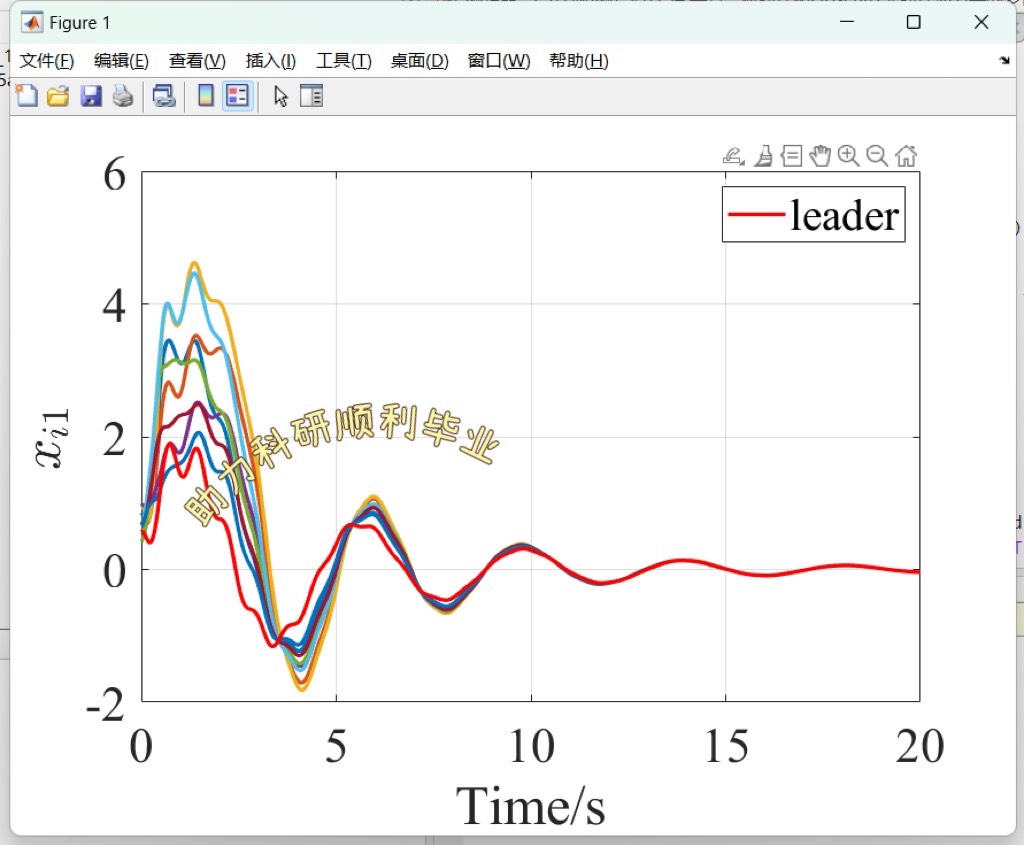
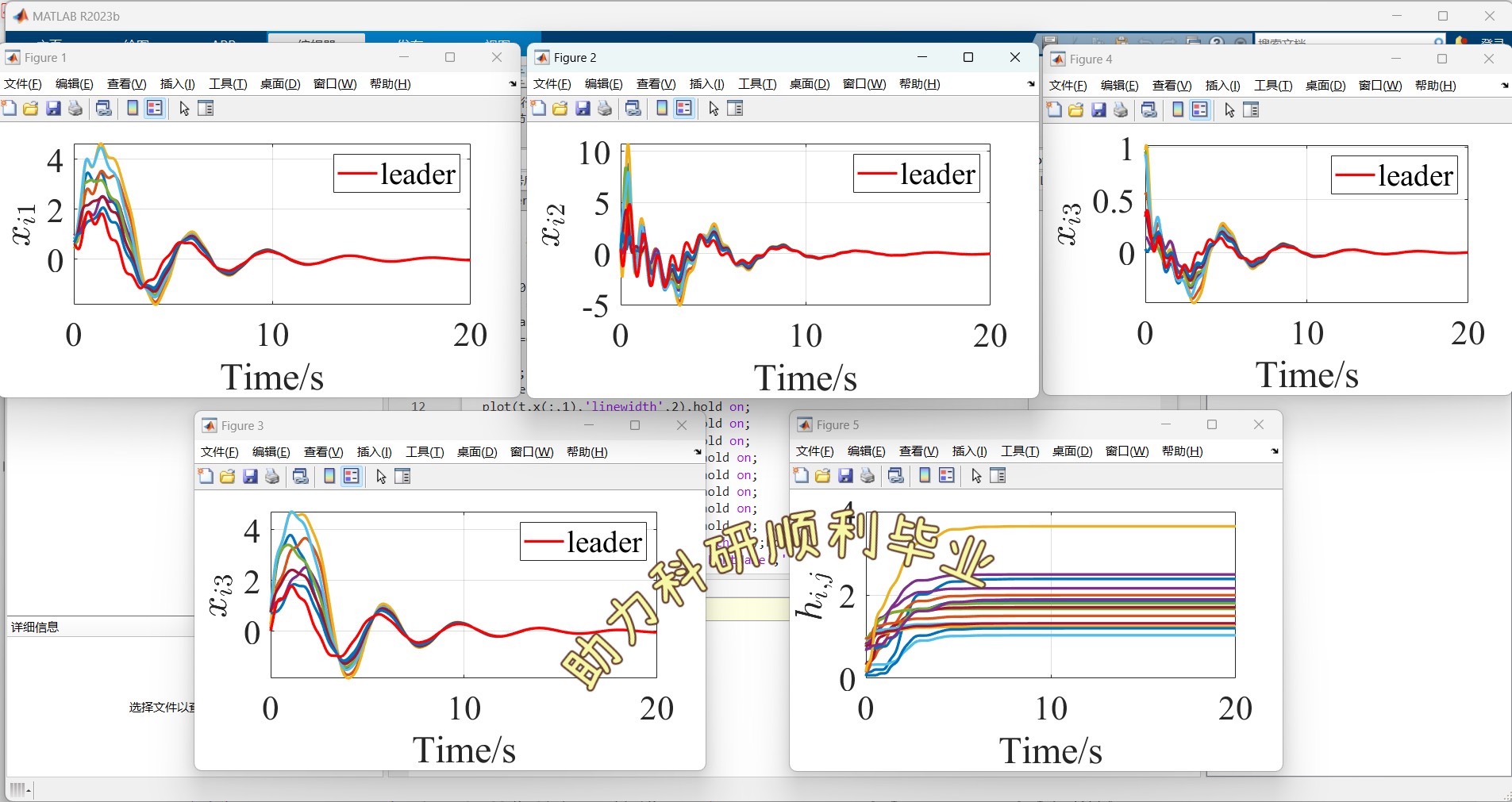
4. 求解与绘图：同样使用 ode45 函数求解常微分方程，并绘图展示每个智能体状态随时间的变化。从图中能清晰看到追随者的状态逐渐向领导者状态靠拢，实现了领导者 - 追随者一致性。

通过以上代码示例和分析，我们能对顶刊TAC中多智能体分布式自适应一致性控制有更直观深入的理解，无论是纯一致性还是领导者 - 追随者一致性，都为多智能体系统在众多领域的应用提供了坚实的理论和实践基础。