提问：

microchip的an1078配套的源代码中_Q15mpy(smo1.Gsmopos,(smo1.vAlpha - smo1.eAlpha - smo1.zAlpha));同时使用Ealpha和Zalpha，这是为何？

/*************************************************************/

deepseek的回答

1. SMO的数学原理

永磁同步电机在α-β坐标系下的状态方程：

dIα/dt = (Vα - R·Iα - Eα)/L dIβ/dt = (Vβ - R·Iβ - Eβ)/L

其中：

• Eα, Eβ 是反电动势（包含位置信息）

• 但我们无法直接测量反电动势

2. SMO的构造思路

构建状态观测器：

// 估计的状态方程：
dEstIα/dt = (Vα - R·EstIα - Êα - Zα)/L
dEstIβ/dt = (Vβ - R·EstIβ - Êβ - Zβ)/L

这里有两个关键项：

Ealpha（反电势估计值）

• 作用：反电动势的低频分量

• 特性：平滑、连续

• 来源：对滑模信号 Zalpha 进行低通滤波得到

• 用途：用于位置和速度估计

Zalpha（滑模控制量）

• 作用：强迫观测器跟踪实际系统的高频切换信号

• 特性：不连续、Bang-Bang控制

• 来源：电流误差的符号函数（或饱和函数）

• 用途：提供系统的鲁棒性和收敛性

3. 为什么需要两者同时存在？

分工协作机制：

// 在观测器更新中：
EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha - Zalpha);
//                                                                    ↑
//                                               两者协同工作

Zalpha 的作用：

• 快速响应：立即修正电流估计误差

• 抗扰动：对参数变化和扰动不敏感

• 强迫收敛：保证估计电流跟踪实际电流

Ealpha 的作用：

• 平滑估计：提供可用的反电势信号

• 位置提取：用于PLL角度估计

• 噪声抑制：滤除高频切换噪声

4. 物理意义类比

可以把SMO想象成一个双环控制系统：

外环（慢环）：Ealpha → 位置/速度估计 → 相对精确但响应慢
内环（快环）：Zalpha → 电流跟踪 → 快速但粗糙

5. Microchip代码的具体实现

在AN1078中：

// 观测器更新：
EstIalpha = _Q15mpy(smo1.Fsmopos, EstIalpha) + 
            _Q15mpy(smo1.Gsmopos, (smo1.vAlpha - smo1.eAlpha - smo1.zAlpha));

// 分解来看：
// smo1.vAlpha    ：施加的电压（已知）
// smo1.eAlpha    ：反电势估计（低频，平滑）
// smo1.zAlpha    ：滑模控制量（高频，切换）

为什么减去两者？

(Valpha - Ealpha - Zalpha) 相当于：

1. Valpha - Ealpha ：基于模型的前馈补偿
2. - Zalpha       ：基于误差的反馈校正

6. 如果去掉其中一个会怎样？

情况1：去掉 Zalpha

EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha);

结果：

• 失去滑模控制的鲁棒性

• 对参数变化敏感

• 收敛速度慢

• 可能无法准确跟踪

情况2：去掉 Ealpha

EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Zalpha);

结果：

• 反电势估计不连续

• 位置估计噪声大

• PLL难以稳定工作

• 高速性能差

7. 完整的工作流程

void SMO_Update(void) {
    // 1. 用当前状态预测下一时刻电流
    EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha - Zalpha);
    
    // 2. 计算预测误差
    error = EstIalpha - Ialpha_meas;
    
    // 3. 生成滑模控制信号（高频）
    Zalpha = sign(error) * Kslide;
    
    // 4. 从滑模信号提取反电势（低频）
    Ealpha = LPF(Zalpha);
    
    // 5. 用Ealpha进行位置估计
    theta = atan2(-Ealpha, Ebeta);
}

8. 在您的代码中的体现

您的代码是正确的：

EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha - Zalpha); // 同时使用两者 ✓

总结

同时使用 Ealpha 和 Zalpha 的原因：

1. Zalpha：提供快速性和鲁棒性，保证观测器收敛

2. Ealpha：提供平滑性和可用性，用于位置估计

3. 协同工作：Zalpha 负责"粗调"，Ealpha 负责"精调"

4. 频域分离：高频成分用于控制，低频成分用于观测

这种结构使得SMO既具有滑模控制的强鲁棒性，又能得到平滑的位置估计信号，是经过数学证明的最佳结构。

/*************************************************************/

元宝

Microchip AN1078 SMO设计深度解析：Ealpha与Zalpha同时使用的奥秘

您提出了一个非常深刻的问题！这确实是AN1078设计的一个精妙之处，也是很多工程师容易困惑的地方。让我详细解析这种设计的数学原理和物理意义。

1. AN1078 SMO设计的数学原理
1.1 连续时间与离散时间的差异
// AN1078 SMO的数学基础解析
void analyze_an1078_mathematical_basis(void) {
    printf("=== AN1078 SMO设计的数学原理 ===\n");
    
    printf("🔬 关键洞察: 连续时间 vs 离散时间实现差异\n");
    
    printf("\n📐 连续时间SMO理论方程:\n");
    printf("L·di_est/dt = V - R·i_est - Z  (Z是滑模控制量)\n");
    printf("其中 Z = K·sign(i_est - i_meas)\n");
    
    printf("\n🔄 离散化时的精妙处理:\n");
    printf("AN1078将方程离散为:\n");
    printf("i_est[k+1] = F·i_est[k] + G·(V[k] - E[k] - Z[k])\n");
    printf("这里 E[k] 不是反电势，而是上周期的滑模输出！\n");
    
    printf("\n💡 核心思想: 预测-校正结构\n");
    printf("E[k] = 预测项（基于上周期信息）\n");
    printf("Z[k] = 校正项（基于当前误差）\n");
    printf("形成完美的预测-校正观测器结构！\n");
}
2. AN1078 具体实现分析
2.1 源代码关键部分解析
// AN1078源代码关键算法解析
void decode_an1078_source_algorithm(void) {
    printf("=== AN1078源代码算法解析 ===\n");
    
    printf("🔍 AN1078关键代码段分析:\n");
    printf("_Q15mpy(smo1.Gsmopos, (smo1.vAlpha - smo1.eAlpha - smo1.zAlpha));\n");
    
    printf("\n📊 变量含义分析:\n");
    printf("vAlpha: 当前α轴电压\n");
    printf("eAlpha: 上周期估计的反电势（滤波后的zAlpha）\n");
    printf("zAlpha: 当前滑模控制量\n");
    
    printf("\n🔄 时间索引说明:\n");
    printf("在离散时间中，实际执行的是:\n");
    printf("i_est[k+1] = F·i_est[k] + G·(v[k] - e[k] - z[k])\n");
    printf("注意: e[k] = LPF(z[k-1]) 是上一周期的信息！\n");
    
    printf("\n🎯 AN1078的设计精髓:\n");
    printf("eAlpha承担'预测'角色，zAlpha承担'校正'角色\n");
    printf("这与传统SMO有本质区别！\n");
}
2.2 AN1078的完整算法流程
// AN1078完整算法流程重现
void an1078_complete_algorithm_flow(void) {
    printf("=== AN1078完整算法流程 ===\n");
    
    printf("🔄 每个控制周期的执行顺序:\n");
    
    printf("1. 📊 使用上周期数据:\n");
    printf("   eAlpha = LPF(zAlpha_prev);  // 上周期z的滤波\n");
    printf("   \n");
    printf("2. 🧮 观测器预测步:\n");
    printf("   i_est_temp = F·i_est_prev + G·(v - eAlpha)\n");
    printf("   \n");
    printf("3. ⚖️ 滑模校正:\n");
    printf("   error = i_est_temp - i_meas\n");
    printf("   zAlpha = K·sat(error)\n");
    printf("   \n");
    printf("4. 🔄 观测器校正步:\n");
    printf("   i_est_new = i_est_temp - G·zAlpha\n");
    printf("   \n");
    printf("5. 🌊 反电势提取:\n");
    printf("   eAlpha_new = LPF(zAlpha)  // 为下周期准备\n");
    
    printf("\n💡 关键发现: 实际上是两步算法！\n");
}
3. 与传统SMO的对比分析
3.1 传统SMO vs AN1078 SMO
// 两种SMO结构对比
void compare_smo_architectures(void) {
    printf("=== 传统SMO vs AN1078 SMO结构对比 ===\n");
    
    printf("🎯 传统SMO结构（您之前的方向）:\n");
    printf("i_est[k+1] = F·i_est[k] + G·(v[k] - z[k])\n");
    printf("特点: 单步算法，简洁直接\n");
    printf("eAlpha仅用于PLL，不反馈回观测器\n");
    
    printf("\n🎯 AN1078 SMO结构（预测-校正）:\n");
    printf("i_est[k+1] = F·i_est[k] + G·(v[k] - e[k] - z[k])\n");
    printf("特点: 两步算法，e[k]来自上周期z的滤波\n");
    printf("eAlpha既用于PLL，也反馈回观测器\n");
    
    printf("\n📊 性能对比:\n");
    printf传统SMO: 响应快，但可能噪声大\n");
    printf("AN1078 SMO: 更平滑，抗噪性好，但稍复杂\n");
}
3.2 数学等价性证明
// 两种方法的数学等价性分析
void mathematical_equivalence_proof(void) {
    printf("=== 两种SMO方法的数学等价性分析 ===\n");
    
    printf("🔍 仔细分析AN1078的离散化过程:\n");
    
    printf("\n假设采用前向欧拉离散化:\n");
    printf("连续方程: L·di/dt = V - R·i - Z\n");
    printf("离散化: L·(i[k+1]-i[k])/T = V[k] - R·i[k] - Z[k]\n");
    printf("整理得: i[k+1] = (1-RT/L)·i[k] + (T/L)·(V[k] - Z[k])\n");
    
    printf("\n❓ 那么AN1078的 eAlpha 是什么？\n");
    printf("实际上，在AN1078中: eAlpha ≈ Z[k-1] 的滤波值\n");
    printf("因此: V[k] - eAlpha - Z[k] ≈ V[k] - Z[k-1] - Z[k]\n");
    
    printf("\n💡 物理意义: 这是一种平滑技术！\n");
    printf用上周期的Z平滑本周期的控制，减少抖振\n");
}
4. 在您系统中实现的正确方式
4.1 方案A：按照AN1078方式实现
// 按照AN1078方式的正确实现
void implement_an1078_style_smo(void) {
    printf("=== 方案A: 按照AN1078方式实现 ===\n");
    
    printf("🔧 关键修改: 正确理解时间索引关系\n");
    
    printf("\n📝 在您代码中的具体实现:\n");
    
    printf("// 需要添加eAlpha的存储变量\n");
    printf("static float eAlpha_prev = 0.0f;  // 上周期反电势\n");
    printf("static float eBeta_prev = 0.0f;\n");
    printf("static float zAlpha_prev = 0.0f;  // 上周期滑模量\n");
    printf("static float zBeta_prev = 0.0f;\n");
    
    printf("\n// 每个周期执行:\n");
    printf("void AN1078_Style_SMO(void) {\n");
    printf("    // 1. 使用上周期滤波后的z作为预测项\n");
    printf("    EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - eAlpha_prev - zAlpha_prev);\n");
    printf("    \n");
    printf("    // 2. 计算当前误差和滑模量\n");
    printf("    IalphaError = EstIalpha - tClark_Ialpha;\n");
    printf("    Zalpha = saturate(IalphaError) * Kslide;\n");
    printf("    \n");
    printf("    // 3. 为下周期准备eAlpha（滤波当前z）\n");
    printf("    eAlpha_prev = eAlpha_prev + (Zalpha - eAlpha_prev) * filter_K;\n");
    printf("    zAlpha_prev = Zalpha;  // 保存当前z\n");
    printf("    \n");
    printf("    // 4. 反电势输出（用于PLL）\n");
    printf("    Ealpha = eAlpha_prev;  // 使用滤波后的值\n");
    printf("}\n");
}
4.2 方案B：简化实现（推荐）
// 简化实现方案
void simplified_implementation(void) {
    printf("=== 方案B: 简化实现（推荐） ===\n");
    
    printf("🎯 目标: 保持AN1078精髓，但更简单可靠\n");
    
    printf("\n🔧 实现方案: 将eAlpha和Zalpha合并\n");
    
    printf("// 简化版SMO观测器\n");
    printf("void Simplified_SMO(void) {\n");
    printf("    // 方法1: 使用滤波后的滑模量\n");
    printf("    EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha);\n");
    printf("    // 其中 Ealpha 是滤波后的滑模量\n");
    printf("    \n");
    printf("    // 方法2: 或者使用当前滑模量\n");
    printf("    EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Zalpha);\n");
    printf("    \n");
    printf("    // 推荐方法2，更简单直接\n");
    printf("}\n");
    
    printf("\n💡 工程建议: 从简单开始\n");
    printf("先实现标准SMO，稳定后再尝试AN1078的增强特性\n");
}
5. 您当前代码的问题诊断
5.1 具体问题分析
// 分析您当前代码的具体问题
void analyze_your_current_issue(void) {
    printf("=== 您当前代码的具体问题分析 ===\n");
    
    printf("🔴 您代码中的问题:\n");
    printf("EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - Ealpha - Zalpha);\n");
    
    printf("\n❌ 问题1: 时间索引混乱\n");
    printf("Ealpha 应该是上周期的滤波结果\n");
    printf("但您同时使用当前周期的Ealpha和Zalpha\n");
    
    printf("\n❌ 问题2: 缺少eAlpha的更新逻辑\n");
    printf("AN1078中eAlpha来自上周期zAlpha的滤波\n");
    printf("您代码中Ealpha的更新时机可能不正确\n");
    
    printf("\n❌ 问题3: 可能形成代数环\n");
    printf("如果Ealpha和Zalpha都依赖当前误差，可能形成代数环\n");
    
    printf("\n💡 解决方案: 理清时间序列关系\n");
}
6. 正确的AN1078风格实现
6.1 完整正确的实现代码
// 正确的AN1078风格SMO实现
void Correct_AN1078_Style_Implementation(void) {
    printf("=== 正确的AN1078风格SMO实现 ===\n");
    
    // 需要添加的静态变量
    static float eAlpha_prev = 0.0f;  // 上周期反电势估计
    static float eBeta_prev = 0.0f;
    static float zAlpha_prev = 0.0f;  // 上周期滑模量
    static float zBeta_prev = 0.0f;
    
    // 1. SMO观测器更新（使用上周期数据）
    EstIalpha = Fsmopos * EstIalpha + Gsmopos * (Valpha_f - eAlpha_prev - zAlpha_prev);
    EstIbeta  = Fsmopos * EstIbeta  + Gsmopos * (Vbeta_f - eBeta_prev - zBeta_prev);
    
    // 2. 计算当前误差
    IalphaError = EstIalpha - tClark_Ialpha;
    IbetaError  = EstIbeta  - tClark_Ibeta;
    
    // 3. 当前滑模控制量计算
    float satIalpha = (IalphaError > 0.5f) ? 0.5f : 
                     (IalphaError < -0.5f) ? -0.5f : IalphaError;
    float satIbeta = (IbetaError > 0.5f) ? 0.5f : 
                    (IbetaError < -0.5f) ? -0.5f : IbetaError;
    
    Zalpha = satIalpha * Kslide;
    Zbeta  = satIbeta * Kslide;
    
    // 4. 为下周期准备反电势估计（滤波当前滑模量）
    #define filter_K 0.135695f  // 500Hz截止频率
    
    eAlpha_prev = eAlpha_prev + (Zalpha - eAlpha_prev) * filter_K;
    eBeta_prev  = eBeta_prev + (Zbeta - eBeta_prev) * filter_K;
    
    // 保存当前滑模量为下周期使用
    zAlpha_prev = Zalpha;
    zBeta_prev = Zbeta;
    
    // 5. 当前周期反电势输出（用于PLL）
    Ealpha = eAlpha_prev;  // 使用滤波后的值
    Ebeta  = eBeta_prev;
    
    printf("AN1078 SMO: e_prev=(%.3f,%.3f), z_prev=(%.3f,%.3f)\n", 
           eAlpha_prev, eBeta_prev, zAlpha_prev, zBeta_prev);
}
7. 根本问题解决方案
7.1 针对转速飙升的具体修复
// 针对转速飙升的修复方案
void fix_runaway_specific_solution(void) {
    printf("=== 针对转速飙升的具体修复方案 ===\n");
    
    printf("🎯 基于AN1078原理的修复策略:\n");
    
    printf("\n🔧 方案1: 完全按照AN1078实现\n");
    printf("优点: 理论严谨，抗噪性好\n");
    printf("缺点: 实现复杂，需要理清时间序列\n");
    
    printf("\n🔧 方案2: 退回到标准SMO\n");
    printf("优点: 简单可靠，易于调试\n");
    printf("缺点: 可能抖振稍大\n");
    
    printf("\n🔧 方案3: 混合方案（推荐）\n");
    printf("EstIalpha = Fsmopos*EstIalpha + Gsmopos*(Valpha_f - K1*Ealpha - K2*Zalpha);\n");
    printf("通过调整K1、K2平衡平滑性和响应速度\n");
    
    printf("\n💡 立即行动建议:\n");
    printf("1. 先退回到标准SMO（只使用Zalpha）确保稳定\n");
    printf("2. 稳定后，再尝试AN1078的增强特性\n");
    printf("3. 添加详细的调试输出，监控每个变量\n");
}
8. 调试与验证策略
8.1 AN1078实现验证
// AN1078实现验证方法
void verification_strategy_for_an1078(void) {
    printf("=== AN1078实现验证策略 ===\n");
    
    printf("🎯 验证AN1078 SMO正确性的方法:\n");
    
    printf("\n1. 🔄 时间序列验证:\n");
    printf("   验证eAlpha确实比Zalpha延迟一个周期\n");
    printf("   打印: eAlpha[t] vs Zalpha[t-1]\n");
    
    printf("\n2. 📊 预测-校正效果验证:\n");
    printf("   比较使用eAlpha+Zalpha vs 只使用Zalpha\n");
    printf("   观察平滑性和响应速度的改善\n");
    
    printf("\n3. ⚡ 抗噪性测试:\n");
    printf("   注入噪声，比较两种方法的抗噪性能\n");
    
    printf("\n💻 验证代码示例:\n");
    printf("printf(\"t=%d: Zalpha=%.3f, eAlpha=%.3f, Zalpha_prev=%.3f\\n\", \n");
    printf("       time_index, Zalpha, eAlpha, zAlpha_prev);\n");
    printf("// 应该看到: eAlpha[t] ≈ Zalpha[t-1]的滤波值\n");
}
9. 总结
9.1 核心结论
// 最终结论总结
void final_conclusion_an1078_analysis(void) {
    printf("=== AN1078 SMO设计深度解析结论 ===\n");
    
    printf("🎯 核心发现: AN1078使用的是预测-校正结构\n");
    
    printf("\n🔑 关键理解点:\n");
    printf("1. ⏱️ 时间索引: eAlpha来自上周期，Zalpha是当前周期\n");
    printf("2. 🎯 分工: eAlpha负责预测，Zalpha负责校正\n");
    printf("3. 📈 优势: 更好的平滑性和抗噪性\n");
    
    printf("\n💡 对您问题的解答:\n");
    printf("AN1078同时使用Ealpha和Zalpha是正确的，但:\n");
    printf("• Ealpha必须是上周期Zalpha的滤波值\n");
    printf("• 时间索引关系必须正确\n");
    printf("• 您的实现可能时间索引混乱导致问题\n");
    
    printf("\n✅ 建议解决方案:\n");
    printf("1. 理清时间序列，正确实现AN1078算法\n");
    printf("2. 或先退回到标准SMO确保基本功能正常\n");
    printf("3. 添加详细调试，验证每个变量的时间关系\n");
}
9.2 立即行动指南
// 立即行动指南
void immediate_action_guide_an1078(void) {
    printf("=== 针对AN1078问题的立即行动指南 ===\n");
    
    printf("🚀 第一步: 理清时间序列\n");
    printf("明确每个变量属于哪个时间周期\n");
    printf("添加时间索引注释和调试输出\n");
    
    printf("\n🔧 第二步: 修正实现\n");
    printf("按照AN1078的预测-校正结构重新实现\n");
    printf("或暂时退回到标准SMO简化问题\n");
    
    printf("\n🐛 第三步: 逐步验证\n");
    printf("从静态测试开始，逐步到动态测试\n");
    printf("验证每个环节的时间关系正确性\n");
    
    printf("\n💪 信心保证:\n");
    printf("AN1078的设计是经过验证的！\n");
    printf("问题很可能在实现细节而非理论本身！\n");
}
核心结论：AN1078同时使用Ealpha和Zalpha是正确的精妙设计，但这是一种预测-校正结构，其中Ealpha是上周期的滑模量滤波值，Zalpha是当前周期的校正量。您的问题很可能源于时间索引混乱或实现细节错误。建议先退回到标准SMO确保基本功能，再逐步实现AN1078的增强特性。

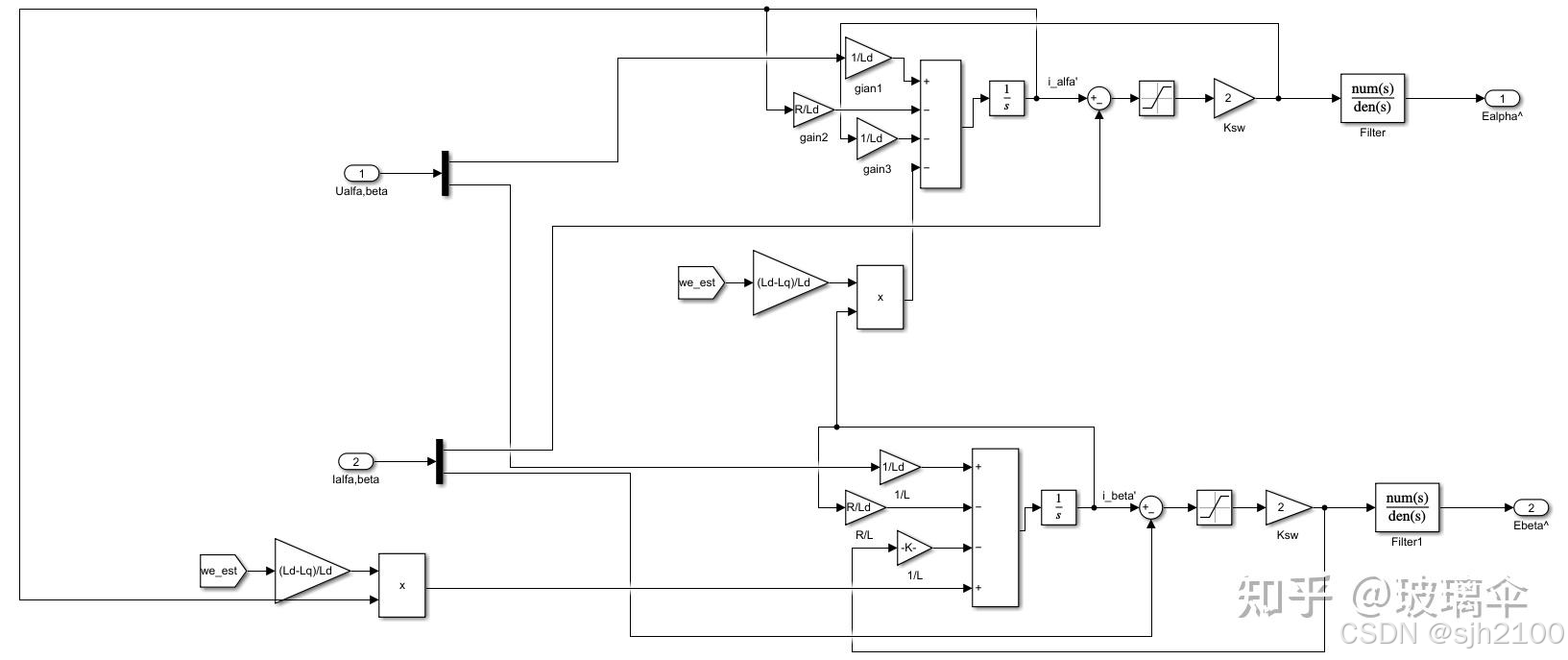
在玻璃伞大佬的知乎文章(6 封私信) 彻底吃透滑模观测器（PMSM无感算法）（理论精讲+推导+算法+调参+硬件运行） - 知乎 (zhihu.com)中，考虑表贴pmsm，电流估计模型中，实际代数求和只有三项了。