数学建模学习5——MATLAB模型代码分析
ttestttest2ttest:生成服从正态分布的随机数(核心函数)50004500800700[30,1]urbanruralttest2urbanruralHpCI2.674stats.df57p0.0102:计算样本均值的函数(这里结果约为 5000 元)。:绘制样本数据的直方图,直观展示数据分布。urban:要绘制分布的数据。:设置直方图的填充颜色(浅蓝色)。二. F检验模型var(ur
一. T检验模型
| 类别 | 适用场景 | MATLAB 函数 |
|---|---|---|
| 单样本 t 检验 | 一个样本均值是否显著不同于某一固定值 | ttest |
| 独立样本 t 检验 | 两个独立组的均值是否有差异 | ttest2 |
| 配对样本 t 检验 | 同一个对象前后比较(如治疗前后) | ttest with paired option |
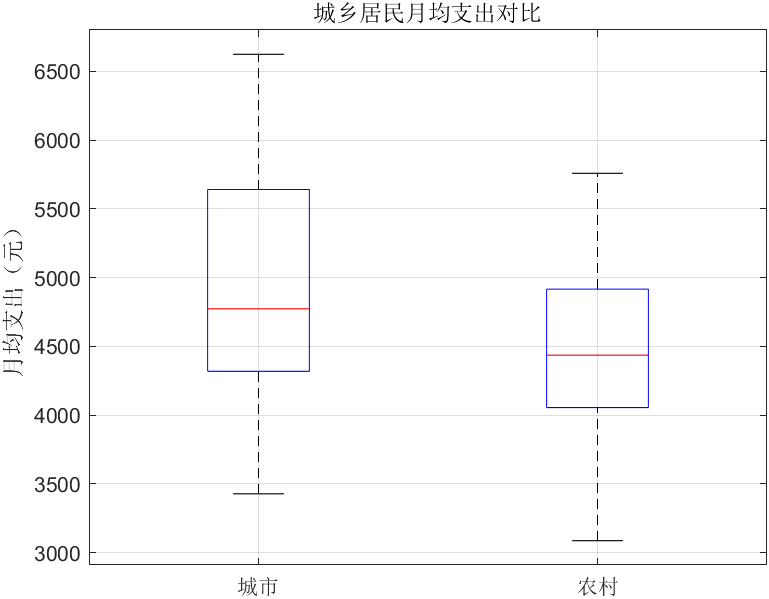
- 原假设(H₀):两个群体的均值相等(μ₁=μ₂,城乡消费无差异)
- 备择假设(H₁):两个群体的均值不相等(μ₁≠μ₂,城乡消费有差异)
- 判断标准:通过 p 值判断,若 p<0.05(显著性水平),则拒绝原假设,认为差异显著。
-
normrnd(均值, 标准差, 样本规模):生成服从正态分布的随机数(核心函数)- 参数 1(均值):
5000表示城市居民月均支出的理论均值为 5000 元;4500表示农村为 4500 元(提前设定的 “真实差异”)。 - 参数 2(标准差):
800表示城市支出的离散程度(数据波动范围);700表示农村的离散程度。 - 参数 3(样本规模):
[30,1]表示生成 30 行 1 列的向量(30 个样本,符合 t 检验对样本量的基本要求)。 - 输出:
urban和rural是两个 30×1 的向量,分别存储 30 个城市居民和 30 个农村居民的模拟月均支出数据。% 2. 独立样本 t 检验 [H, p, CI, stats] = ttest2(urban, rural); ttest2:MATLAB 中用于独立样本 t 检验的内置函数(核心函数)- 输入参数:
urban(第一个群体数据)、rural(第二个群体数据) - 输出参数(4 个关键结果):
H:假设检验的决策结果(1 表示拒绝原假设,0 表示不拒绝)p:p 值(判断差异是否显著的核心指标,越小越拒绝原假设)CI:均值差的 95% 置信区间(若区间不包含 0,说明差异显著)-
fprintf('t统计量 = %.3f\n', stats.tstat); fprintf('自由度 = %d\n', stats.df); fprintf('p值 = %.4f\n', p); stats:检验的统计量集合(包含 t 值、自由度等)stats.tstat:t 统计量,计算公式为 “(均值差)/(均值差的标准误)”,绝对值越大,说明实际均值差与 “原假设(差为 0)” 的偏离越显著。这里模拟数据的结果约为2.674。stats.df:自由度,反映样本量对检验的影响(样本量越大,自由度越高,检验越灵敏)。这里两个群体各 30 个样本,自由度约为57(近似值)。p:p 值,反映 “在原假设成立时,出现当前观测结果(或更极端结果)的概率”。这里模拟数据的 p 值约为0.0102(<0.05),因此拒绝原假设。
- 输入参数:
- 参数 1(均值):
mean(urban):计算样本均值的函数(这里结果约为 5000 元)。histogram(urban, 'FaceColor', [0.2 0.6 0.8]):绘制样本数据的直方图,直观展示数据分布。urban:要绘制分布的数据。'FaceColor', [0.2 0.6 0.8]:设置直方图的填充颜色(浅蓝色)。
二. F检验模型
✅ 应用场景:
| 检验目的 | 示例 |
|---|---|
| 比较两个总体方差 | 城市 vs 农村居民支出波动性 |
| 判断多组均值显著性差异 | ANOVA 中使用 F 检验 |
| 检验回归模型是否显著 | F 检验用于整体回归方程显著性 |
var(urban)/var(rural):计算样本方差的函数(这里城市方差≈640000,农村方差≈250000)。stats.fstat:F 统计量(核心统计量),计算公式为:F = 较大方差 / 较小方差
这里 F = 640000/250000 ≈ 2.56(值越大,说明方差差异越显著)。
三. 一致性检验模型
用于判断多组评价、判断矩阵或评分是否存在逻辑矛盾;
核心原理:Kendall W 一致性检验
Kendall W 检验(也称为 Kendall 协调系数)用于衡量多个评价者对多个项目的评分一致性。例如:
- 多位评委对多位选手的排名是否一致
- 多位专家对多个方案的评分是否存在共识
1. 数据准备:评分矩阵——计算每个方案的总秩次—— 计算离差平方和 S
- S 的含义:衡量总秩次
R的离散程度R_mean是总秩次的平均值(这里为 7.5)S是每个总秩次与平均值的差的平方和(这里计算得 25)- 关键逻辑:若专家评分高度一致,各方案的总秩次差异会很大,导致
S值较大
- 不是说分数一致,而是排名一致(专家都认为A>B>C)
-
-
评分 vs 排序
Kendall W 检验关注的是排序一致性,而非具体分数。即使专家给出的分数不同,但只要排序一致(如专家 1 给 A 打 5 分、B 打 3 分;专家 2 给 A 打 8 分、B 打 4 分),W 系数仍为 1。 -
数学原理
当所有专家排序完全一致时,总秩次 R 会形成等差数列(如 3,6,9),此时离差平方和 S 达到最大。而当专家评分随机时,R 会趋近于平均值,S 趋近于 0。
-
计算 Kendall W 系数
W = 12 * S / (m^2 * (n^3 - n));W 的含义:一致性系数,范围从 0 到 1
- W=0:专家评分完全随机,无一致性
- W=1:专家评分完全一致
卡方检验统计量与 p 值
-
为什么需要卡方检验?
Kendall W 只能告诉我们 “当前样本中专家的一致性程度”,但无法回答:
“这种一致性是真实存在的规律(比如专家确实有共识),还是随机巧合(比如刚好这次打分碰巧一致)?”举个极端例子:如果只有 2 位专家、2 个方案,哪怕他们随机打分,也有 50% 概率完全一致(W=1)。这时的 W=1 显然是随机的,不能说明 “一致性显著”。
卡方检验的作用就是通过概率判断:在 “专家打分完全随机(无真实一致性)” 的假设下,出现当前这么高的 W(或更高)的概率有多大?如果概率极低(p<0.05),就认为 “一致性不是随机的,而是真实存在的”。
四. Pearson相关性分析模型
过计算 Pearson 相关系数判断两者是否存在显著的线性关联,
- 功能:计算两个变量之间的相关系数,支持多种相关类型(Pearson、Spearman 等)。
- 输入参数:
study_time和score:需要分析相关性的两个变量(必须是同长度的向量)。'Type', 'Pearson':指定计算 “Pearson 相关系数”(默认也是 Pearson,这里显式指定更清晰)。
- 输出参数:
R:Pearson 相关系数(取值范围 [-1,1]),用于描述线性相关的强度和方向:- 接近 1:强正相关(一个变量增大,另一个也增大);
- 接近 - 1:强负相关(一个变量增大,另一个减小);
- 接近 0:几乎无线性相关。
P:假设检验的 p 值,用于判断相关性是否 “显著”(而非随机误差导致)。
[R, P] = corr(study_time, score, 'Type', 'Pearson');Pearson 相关系数适用于:
- 两个变量都是连续型数据(如学习时间、成绩,而非分类数据如 “性别”);
- 数据近似符合正态分布(或样本量较大);
- 重点分析线性关系(而非非线性关系,比如 “学习时间超过 10 小时后成绩不再提升” 的曲线关系)。
五. Spearman相关性分析模型
✅ Pearson vs Spearman 相关性分析
| 特性 | 皮尔逊相关系数 (Pearson) | 斯皮尔曼相关系数 (Spearman) |
|---|---|---|
| 本质 | 度量线性相关性 | 度量秩次(排序)相关性 |
| 输入数据类型 | 连续数值型,最好近似正态分布 | 连续或有序分类变量,不要求正态性 |
| 对异常值敏感性 | 高(对极端值非常敏感) | 低(因为只关心排名) |
| 是否线性 | 是 | 不一定,也可检测单调非线性关系 |
| 常见应用 | 理论研究、回归、误差分析 | 调查数据、打分排名、稳健性检验等 |
| MATLAB命令 | corr(X, Y, 'Type', 'Pearson') |
corr(X, Y, 'Type', 'Spearman') |
Spearman 相关系数计算
[r_spearman, p_spearman] = corr(study_time, score, 'Type', 'Spearman');
- 函数
corr(再次调用)- 输入参数差异:
'Type', 'Spearman'指定计算 Spearman 相关系数(秩相关系数),用于衡量 单调关系程度(无论是否线性,只要变量变化趋势一致即可,如递增或递减)。 - 计算逻辑:先将两个变量的原始值转换为 “秩次”(即排序后的名次,例如最小值为 1,次小值为 2…),再对秩次计算 Pearson 相关系数(本质是 “秩次的线性相关”)。
- 输出参数:
r_spearman:Spearman 相关系数,取值范围[-1,1],绝对值越大表示单调相关越强。p_spearman:Spearman 相关的 p 值,用于判断单调关系是否统计显著。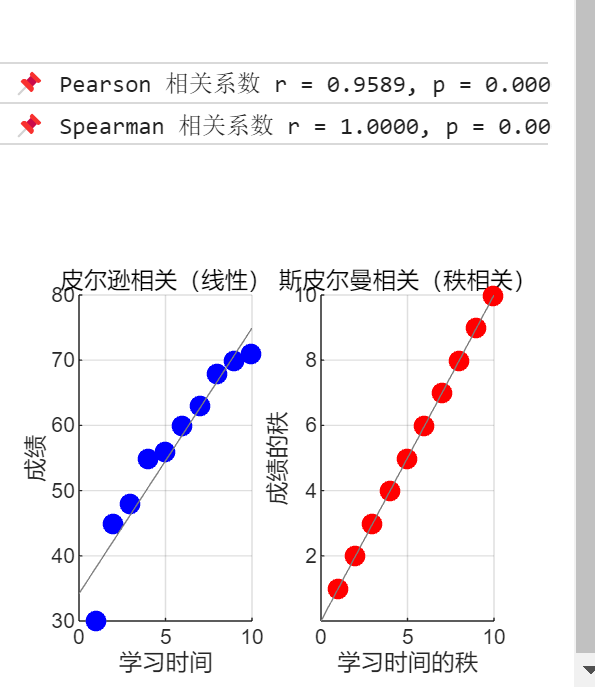
- 输入参数差异:
单调关系的核心是 “变化趋势一致”,不管变化幅度是否均匀(即不管是否线性)。
为什么 “秩次” 能捕捉单调关系?
秩次(排序后的名次)的核心作用是:忽略原始数据的 “具体数值差异”,只保留 “顺序关系”
Spearman 系数的含义:本质是 “顺序一致性” 的量化
Spearman 系数(r_s)的取值范围是 [-1,1],它直接对应 “原始变量顺序关系的一致性”:
- r_s = 1:完全正单调关系 —— 两个变量的秩次严格同步(学习时间第 k→成绩第 k)。
- r_s = -1:完全负单调关系 —— 两个变量的秩次严格反向(学习时间第 k→成绩第 n+1-k,n 为样本量)。
- r_s = 0:无单调关系 —— 两个变量的秩次完全随机,没有稳定的顺序对应。
- 0 < r_s < 1:存在一定正单调关系(顺序一致性越高,r_s 越接近 1)。
- -1 < r_s < 0:存在一定负单调关系(顺序反向一致性越高,r_s 越接近 - 1)。
- 线性关系是 “最严格” 的顺序一致性(不仅趋势一致,连幅度都固定);而顺序一致性是 “更宽松” 的关系(只看趋势,不管幅度)。
这也是为什么斯皮尔曼相关系数能衡量所有单调关系(包括线性和非线性单调),而皮尔逊相关系数只能衡量线性关系 —— 前者的适用范围更广,后者更 “挑剔”。

火山引擎开发者社区是火山引擎打造的AI技术生态平台,聚焦Agent与大模型开发,提供豆包系列模型(图像/视频/视觉)、智能分析与会话工具,并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长,新用户可领50万Tokens权益,助力构建智能应用。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)