💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

分布式控制多智能体系统、PID控制、卡尔曼滤波器的一致性研究

一、引言

二、分布式控制多智能体系统一致性概述

2.1 基本概念

2.2 研究现状

三、PID控制在多智能体系统一致性中的应用

3.1 PID控制原理

3.2 在多智能体系统中的应用策略

3.3 参数调节与优化

四、卡尔曼滤波器在多智能体系统中的作用

4.1 卡尔曼滤波器原理

4.2 在多智能体系统一致性中的应用

五、结论

📚2 运行结果

🎉3 参考文献 

🌈4 Matlab代码实现

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

分布式控制多智能体系统、PID控制、卡尔曼滤波器的一致性研究

摘要：本研究聚焦于分布式控制多智能体系统的一致性问题，深入探讨PID控制与卡尔曼滤波器在其中的应用。首先分析分布式控制多智能体系统一致性的基本概念与研究现状，接着详细阐述PID控制策略对系统一致性的影响及参数调节方式，同时介绍卡尔曼滤波器在处理多智能体系统信息融合与提高一致性方面的作用。通过理论分析、仿真实验等方法，验证所提方法在提升多智能体系统一致性方面的有效性，为多智能体系统在多个领域的广泛应用提供理论支持与实践指导 。

一、引言

在当今科技快速发展的时代，多智能体系统（MAS）在诸如无人机编队飞行、机器人协作作业、智能交通系统等众多领域展现出巨大的应用潜力。分布式控制多智能体系统旨在通过各个智能体之间的局部交互，实现整个系统的全局目标，而系统一致性是衡量其能否有效运行的关键指标。一致性意味着所有智能体经过一定时间的交互后，其状态能够达到一致或协调 。

PID控制作为一种经典且应用广泛的控制策略，因其结构简单、鲁棒性强等优点，在多智能体系统一致性控制中受到关注。然而，将其应用于多智能体系统，如何合理分配控制器参数以确保系统稳定性成为关键问题。卡尔曼滤波器作为一种高效的数据处理工具，能够在存在噪声干扰的情况下，对系统状态进行最优估计，有助于提高多智能体系统信息融合的准确性，进而对系统一致性产生积极影响 。

二、分布式控制多智能体系统一致性概述

2.1 基本概念

多智能体系统由多个自主智能体组成，这些智能体通过网络拓扑结构进行信息交互。在分布式控制模式下，每个智能体仅依据其自身及邻居智能体的信息做出决策和行动。一致性问题可描述为所有智能体的某些状态变量随时间推移趋于相同的值。例如在无人机编队中，所有无人机的位置、速度等状态需达到一致，以实现整齐的编队飞行 。

2.2 研究现状

目前，针对多智能体系统一致性问题已有大量研究。不同的拓扑结构（如有向图、无向图）对一致性的影响被深入分析，同时各种控制策略不断涌现。但在复杂环境下，如存在噪声干扰、通信时延等情况下，实现高效稳定的一致性仍面临挑战。

三、PID控制在多智能体系统一致性中的应用

3.1 PID控制原理

PID控制器由比例（P）、积分（I）、微分（D）三个环节组成。比例环节根据当前误差信号成比例地调节输出；积分环节对误差信号进行积分，消除系统的稳态误差；微分环节则根据误差信号的变化率来提前调整输出，改善系统的动态性能 。

3.2 在多智能体系统中的应用策略

在多智能体系统中应用PID控制，首先要通过变量转换将一致性问题转化为误差系统的渐近稳定性问题。例如，可将智能体的实际状态与期望的一致状态之间的误差作为PID控制器的输入。然后构造Lyapunov函数进行稳定性分析，基于线性矩阵不等式（LMI）给出系统实现一致性的充分条件，以此来确定合适的PID参数 。

3.3 参数调节与优化

合适的PID参数对系统一致性至关重要。可采用试凑法、Ziegler - Nichols方法等传统方法进行初步参数整定，也可利用智能优化算法（如遗传算法、粒子群优化算法）对参数进行优化，以获得更好的控制效果。例如，在存在噪声干扰的环境中，通过优化后的PID参数，系统能够更快地克服干扰，实现一致性 。

四、卡尔曼滤波器在多智能体系统中的作用

4.1 卡尔曼滤波器原理

卡尔曼滤波器是一种基于线性系统状态空间模型的最优递推估计算法。它通过预测和更新两个步骤，在已知系统动态模型和观测数据的情况下，对系统状态进行最优估计。其核心在于能够有效处理系统噪声和观测噪声，提供准确的状态估计值 。

4.2 在多智能体系统一致性中的应用

在多智能体系统中，各个智能体获取的信息往往带有噪声。卡尔曼滤波器可用于对智能体的观测信息进行滤波处理，提高信息的准确性。通过信息融合，智能体能够更准确地了解自身及邻居的状态，从而更好地调整自身行为，有助于实现系统的一致性。例如在机器人协作搬运任务中，卡尔曼滤波器对机器人传感器获取的位置、力等信息进行处理，使机器人能更精确地协作，保持一致的动作 。

五、结论

本研究深入探讨了分布式控制多智能体系统的一致性问题，详细阐述了PID控制和卡尔曼滤波器在其中的应用。理论分析和仿真实验表明，PID控制能够通过合理的参数调节实现多智能体系统的一致性，而卡尔曼滤波器的引入进一步提高了系统对噪声的抵抗能力，缩短了收敛时间，增强了系统的稳定性和一致性。未来的研究可进一步探索在更复杂环境（如时变拓扑结构、非线性系统）下，如何更好地融合PID控制与卡尔曼滤波器等先进技术，以实现多智能体系统更高效、稳定的一致性.

📚2 运行结果

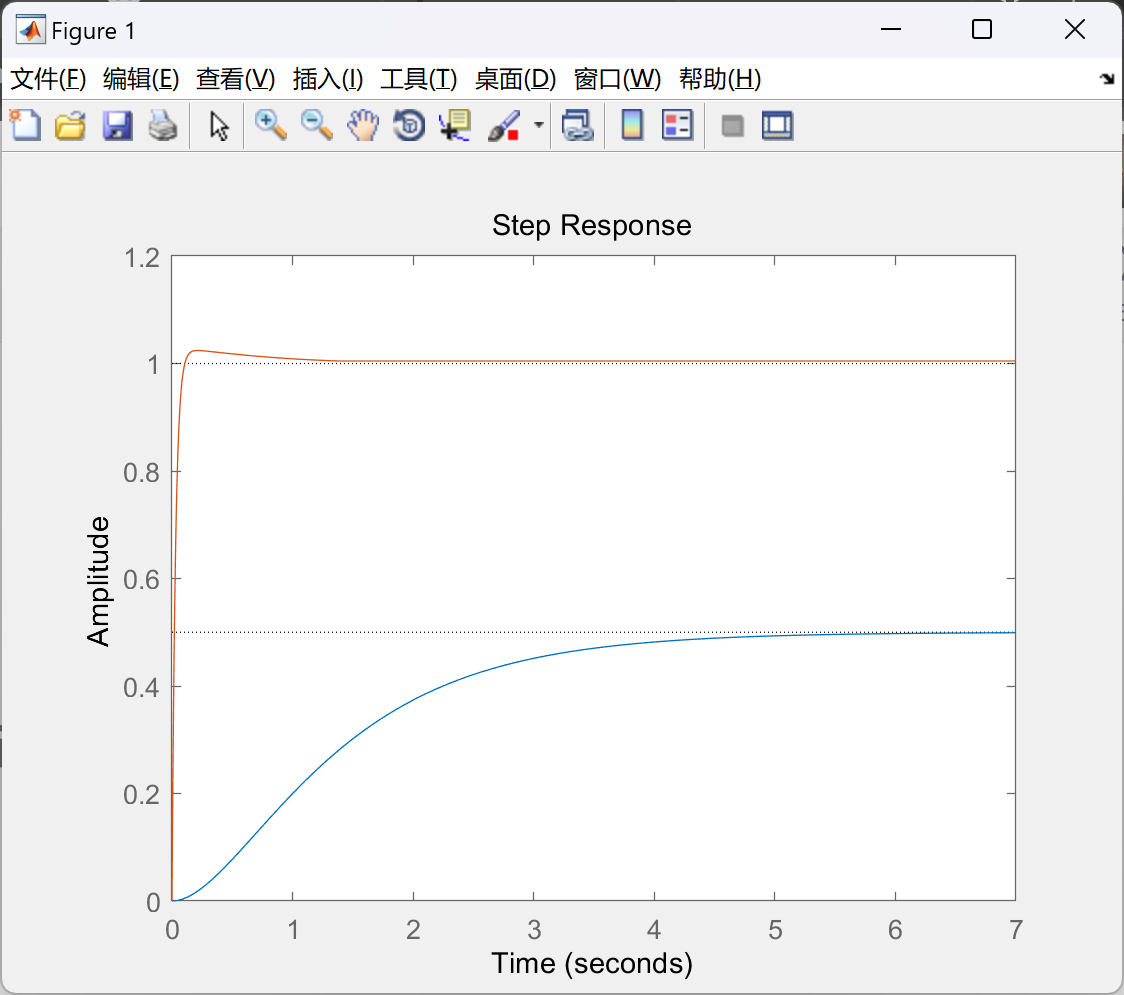
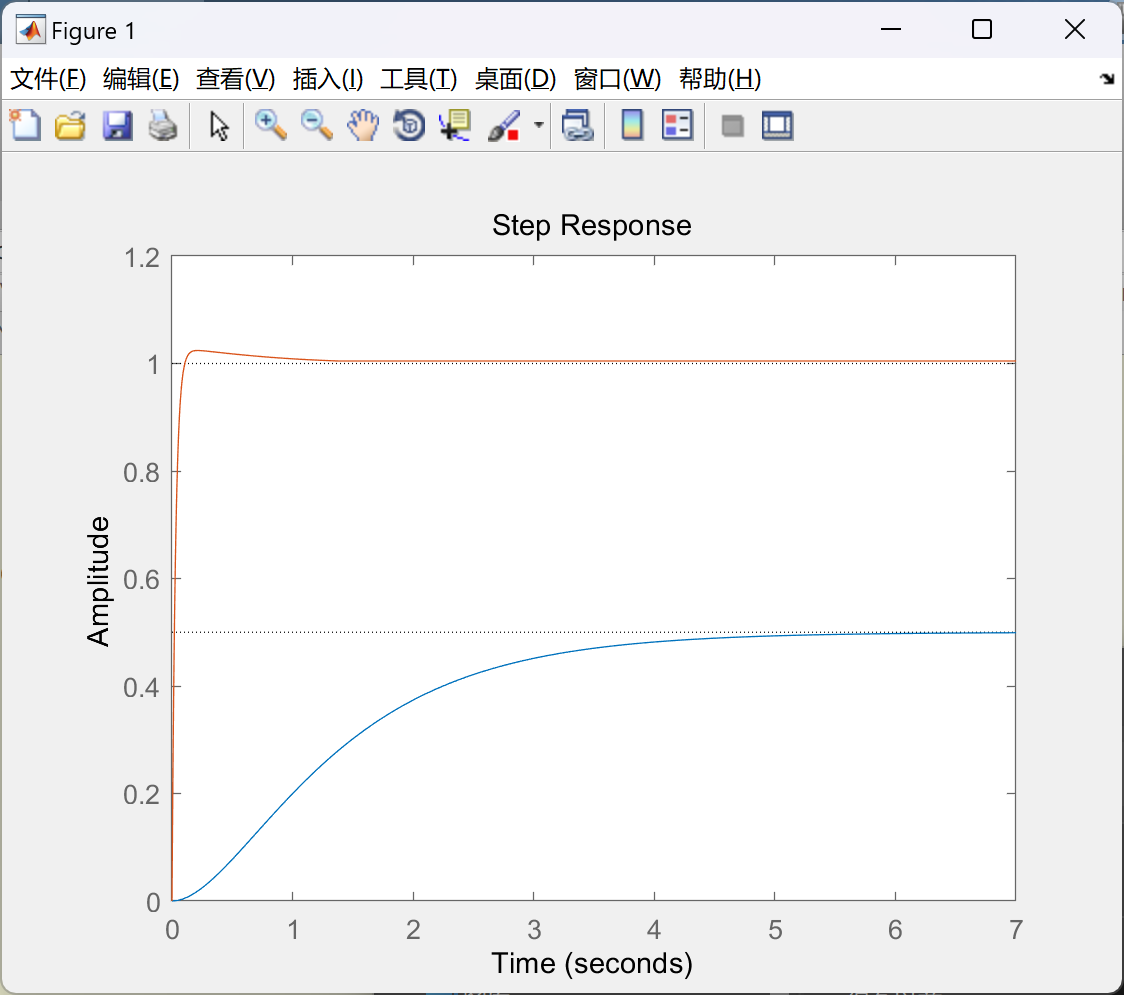
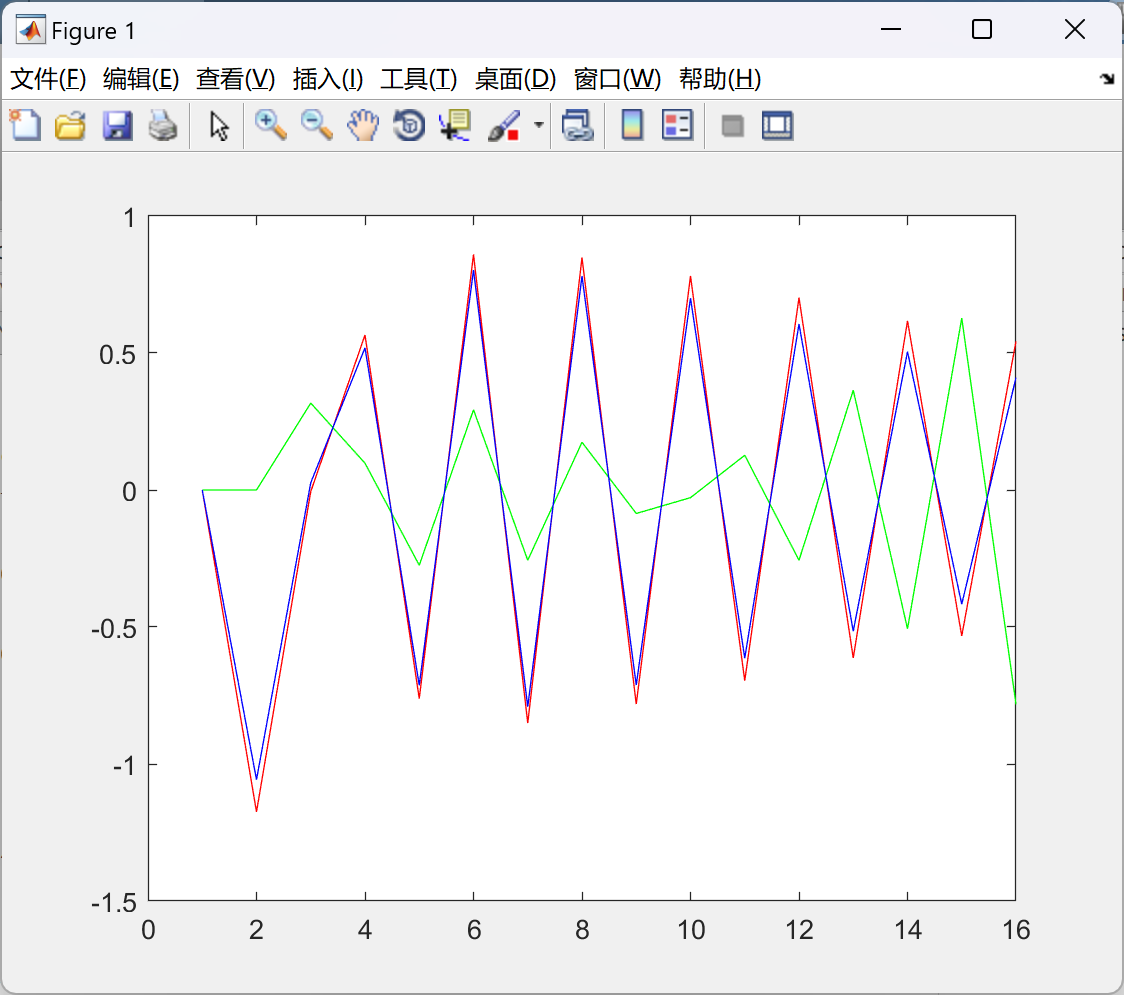
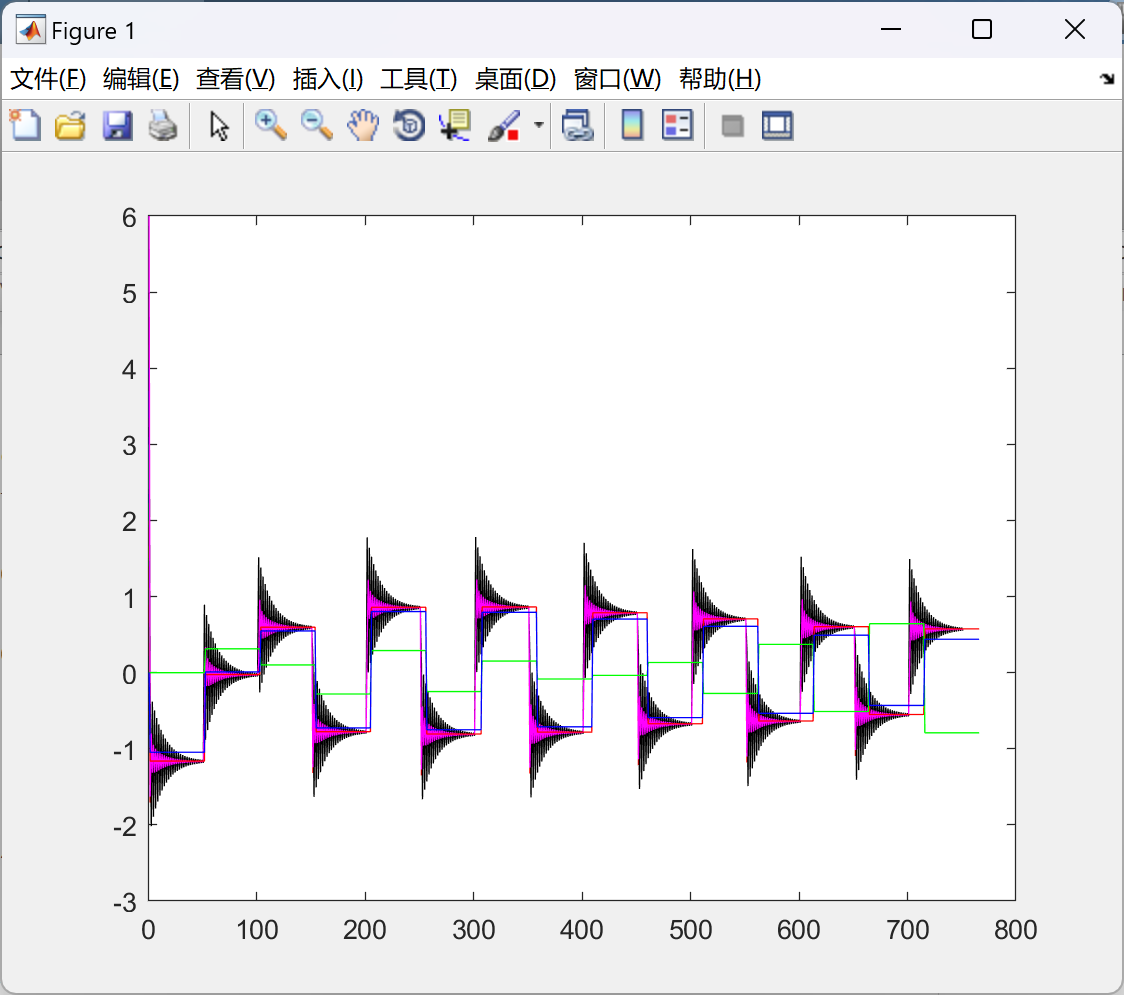
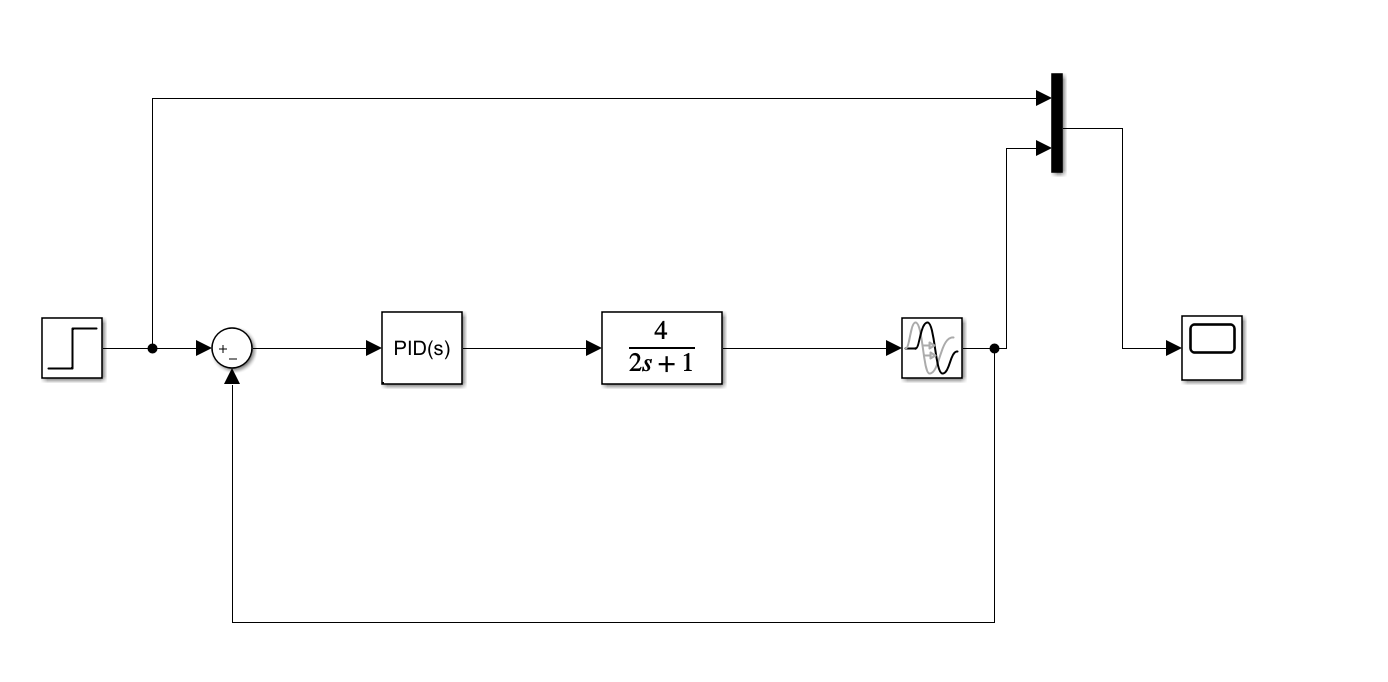
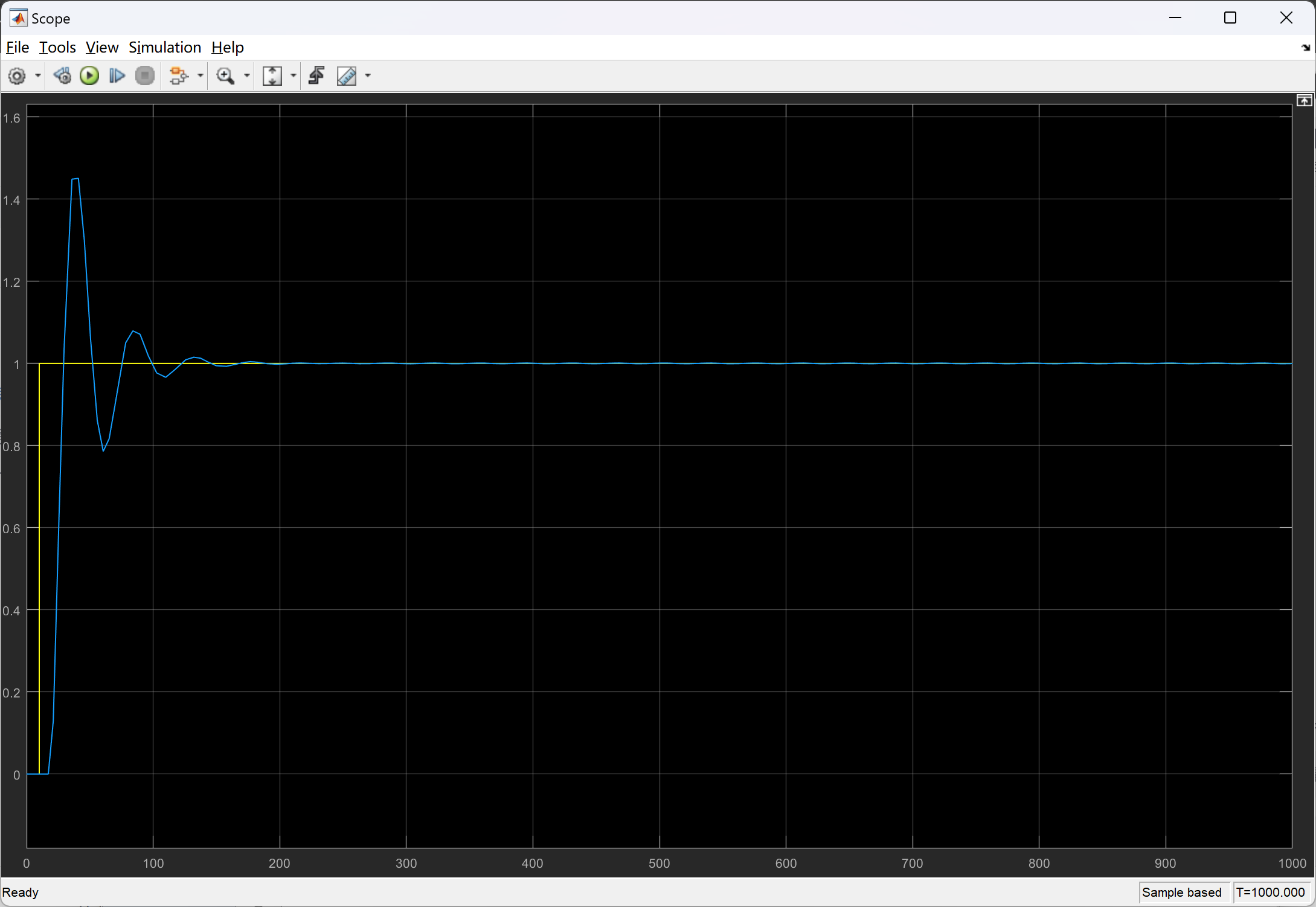
部分代码：

% system intinial state
zx=[4; 4];
zy=0 ;

%estimations
zestx=[0; 0]; % a priori
zesty=0 ;    % a priori
zestxm=0 ; % a posteriori
zestym=0 ; % a posteriori

% aggregation vectors of estimations

zzy=[  0];
zzesty= [  0];    % a priori
zzestym= [  0]; % a posteriori

% Kalman gain
    K=[0.9 ; 0.9];
    

for ii=1:15

    zestx= A*zestx; 
    zesty=C*zestx;% a priori
    
    zx=A*zx+.05*rand(1,1);
    zy=C*zx;
    
    % consensus
    
        %collapse measurements
         x=[zy+1 zy-1 zy-2 zy-1 zy+3 ]';
        
        for jj=1:50
            x=(eye(5)-L/2.6)*x;
            y= [ y x];
        end
        zy=x(1,1);
    
    % end consensus

    
     zestxm=  zestx+K*(zy-zesty)  ;        % a posteriori
     zestym=C*zestxm;    % a posteriori
     zestx=zestxm;
     zzesty=[zzesty  zesty];
     zzestym=[zzestym  C*zestxm];
     zzy= [ zzy   zy];
     

%    add delays to plot consensus procedure  (1/2)
      zzesty=[zzesty  zesty*ones(1,50)];
       zzestym=[zzestym zestym*ones(1,50)    ];
   zzy= [ zzy    zy*ones(1,50)    ]; 
     
     
     
end

% end of simulation

% plotting

%    add delays to plot consensus procedure  (2/2)
  plot (y(1,:), 'red')
    hold on
    plot (y(2,:),'green')
   plot (y(3,:),'blue')
    plot (y(4,:), 'black')
     plot (y(5,:),'magenta')
 

%bita figure
% real, apriori, aposteriori
 plot (zzy(1,:), 'red');
 hold on;
 plot (zzesty(1,:), 'green');
plot (zzestym(1,:), 'blue');

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]马磊,史习智.多智能体系统中一致性卡尔曼滤波的研究进展[J].西南交通大学学报, 2011, 46(2):7.

[2]ZHANG Zhe,WU Jian,HE Cheng,等.基于卡尔曼滤波和增量式PID控制的智能车载系统[J].现代信息科技, 2019(010):003.

[3]林澈.多智能体系统中分布式源点定位与状态估计的研究[D].浙江大学,2017.

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取