机械臂机器人仿真建模，机械臂matlab，机器人仿真、ros机器人，ROS无人机，auv控制机械臂、多杆机械臂、机械臂轨迹规划、多机器人协同、工业机器人、车辆控制器matlab、simulink动力学控制、自适应控制算法、手眼标定 AUBO机械臂开发ROS虚拟机仿真环境机械臂 机器人仿真 正运动学，逆运动学机器人工具箱焊接机器人等六自由度建模能够根据你的模型定制DH参数并且进行相应的运动学逆运动学八组逆解ROS ArmPi FPV机械臂机械臂仿真留学生机械臂 机器人仿真 正运动学，逆运动学，做答疑 matlab 六自由度机器人机械臂 机器人工具箱 DH参数 可接设计 仿真 文献复现运动学分析、工作空间/建模轨迹规划机械臂 机器人 DH参数 运动学 正逆解 urdf建模 轨迹规划。

以下是一个简单的六自由度机械臂的 MATLAB 代码示例，使用机器人工具箱（Robotics Toolbox）进行正运动学和逆运动学分析。这个代码可以帮助你理解如何建模、设置 DH 参数，并计算正运动学和逆运动学。

安装 Robotics Toolbox

首先，请确保你已经安装了 Peter Corke 的 Robotics Toolbox。如果没有安装，可以通过以下命令安装：

% 在 MATLAB 命令窗口中运行以下命令
>> robotInstall

示例代码：六自由度机械臂建模与运动学分析

% 清空工作区
clear; clc;

% 导入 Robotics Toolbox
startup_rvc;

% 定义机械臂的 DH 参数 (Denavit-Hartenberg 参数)
% 格式: [theta, d, a, alpha]
L1 = Link('d', 0.150, 'a', 0, 'alpha', pi/2); % 第1关节
L2 = Link('d', 0, 'a', 0.240, 'alpha', 0);    % 第2关节
L3 = Link('d', 0, 'a', 0.210, 'alpha', 0);    % 第3关节
L4 = Link('d', 0.110, 'a', 0, 'alpha', pi/2); % 第4关节
L5 = Link('d', 0, 'a', 0, 'alpha', -pi/2);    % 第5关节
L6 = Link('d', 0.090, 'a', 0, 'alpha', 0);    % 第6关节

% 创建机械臂模型
robot = SerialLink([L1, L2, L3, L4, L5, L6], 'name', 'SixDOF_Robot');

% 显示机械臂结构
robot.plot([0, 0, 0, 0, 0, 0]); % 默认零角度
robot.display();

%% 正运动学计算
% 输入关节角度 (单位: 弧度)
theta = [0, pi/4, pi/4, pi/6, pi/3, pi/2];

% 计算末端执行器位姿
T = robot.fkine(theta);
disp('末端执行器位姿矩阵:');
disp(T);

%% 逆运动学计算
% 目标末端执行器位姿
T_target = T; % 使用正运动学的结果作为目标

% 求解逆运动学
q_inv = robot.ikine(T_target, 'mask', [1 1 1 1 1 1]); % mask表示自由度约束
disp('逆运动学求解的关节角度:');
disp(q_inv);

%% 绘制机械臂轨迹
% 轨迹规划
t = 0:0.1:2; % 时间向量
q_traj = jtraj([0, 0, 0, 0, 0, 0], theta, t); % 从初始位置到目标位置

% 动画显示
robot.plot(q_traj);

说明

1. DH 参数：根据你的机械臂的实际参数调整 Link 中的 d, a, 和 alpha。
2. 正运动学：通过 fkine 函数计算末端执行器的齐次变换矩阵。
3. 逆运动学：通过 ikine 函数求解八组逆解之一。
4. 轨迹规划：使用 jtraj 函数生成关节空间轨迹。

运行效果

• 正运动学将输出末端执行器的位姿矩阵。
• 逆运动学将返回一组满足目标位姿的关节角度。
• 动画显示机械臂从初始位置移动到目标位置的过程。

如果需要更复杂的功能（如 URDF 建模、ROS 集成等），可以进一步扩展代码或结合 ROS 工具链实现。
根据您提供的机械臂和无人机的图片，我将为您提供一个综合示例代码，该代码结合了MATLAB中的机器人工具箱进行机械臂的正逆运动学分析，并简要介绍了如何在ROS环境中进行仿真。请注意，由于图片中没有具体的尺寸和参数信息，以下代码使用了假设的DH参数。您可以根据实际机械臂的规格调整这些参数。

MATLAB代码：六自由度机械臂的正逆运动学

% 清空工作区
clear; clc;

% 导入 Robotics Toolbox
try
    startup_rvc;
catch
    disp('Robotics Toolbox not found. Please install it first.');
end

% 定义机械臂的 DH 参数 (Denavit-Hartenberg 参数)
L1 = Link([0 0.150 0 pi/2], 'sigma', 0, 'offset', 0); % 第1关节
L2 = Link([0 0 0.240 0], 'sigma', 0, 'offset', 0);    % 第2关节
L3 = Link([0 0 0.210 0], 'sigma', 0, 'offset', 0);    % 第3关节
L4 = Link([0 0.110 0 pi/2], 'sigma', 0, 'offset', 0); % 第4关节
L5 = Link([0 0 0 -pi/2], 'sigma', 0, 'offset', 0);    % 第5关节
L6 = Link([0 0.090 0 0], 'sigma', 0, 'offset', 0);    % 第6关节

% 创建机械臂模型
robot = SerialLink([L1, L2, L3, L4, L5, L6], 'name', 'SixDOF_Robot');

% 显示机械臂结构
robot.plot([0, 0, 0, 0, 0, 0]); % 默认零角度
robot.display();

%% 正运动学计算
% 输入关节角度 (单位: 弧度)
theta = [0, pi/4, pi/4, pi/6, pi/3, pi/2];

% 计算末端执行器位姿
T = robot.fkine(theta);
disp('末端执行器位姿矩阵:');
disp(T);

%% 逆运动学计算
% 目标末端执行器位姿
T_target = T; % 使用正运动学的结果作为目标

% 求解逆运动学
q_inv = robot.ikine(T_target, 'mask', [1 1 1 1 1 1]); % mask表示自由度约束
disp('逆运动学求解的关节角度:');
disp(q_inv);

%% 绘制机械臂轨迹
% 轨迹规划
t = 0:0.1:2; % 时间向量
q_traj = jtraj([0, 0, 0, 0, 0, 0], theta, t); % 从初始位置到目标位置

% 动画显示
robot.plot(q_traj);

ROS环境下的机械臂仿真

对于ROS环境下的机械臂仿真，你需要创建一个URDF文件来描述机械臂的物理结构，然后使用moveit!进行运动规划和控制。以下是一个简单的步骤指南：

1. 创建URDF文件：基于机械臂的CAD模型或图纸，使用urdf_tutorial包创建URDF文件。
2. 配置MoveIt!：使用moveit_setup_assistant为你的机械臂配置MoveIt!。
3. 编写控制节点：使用C++或Python编写ROS节点，利用MoveIt! API进行路径规划和控制。

示例：ROS C++控制节点

#include <ros/ros.h>
#include <moveit/move_group_interface/move_group_interface.h>
#include <geometry_msgs/Pose.h>

int main(int argc, char **argv) {
    ros::init(argc, argv, "move_group_interface_tutorial");
    ros::NodeHandle node_handle;
    ros::AsyncSpinner spinner(1);
    spinner.start();

    // 初始化MoveGroupInterface
    moveit::planning_interface::MoveGroupInterface move_group("arm");

    // 设置目标姿态
    geometry_msgs::Pose target_pose;
    target_pose.orientation.w = 1.0;
    target_pose.position.x = 0.5;
    target_pose.position.y = 0.1;
    target_pose.position.z = 0.6;

    move_group.setPoseTarget(target_pose);

    // 规划并执行运动
    moveit::planning_interface::MoveGroupInterface::Plan my_plan;
    bool success = (move_group.plan(my_plan) == moveit::planning_interface::MoveItErrorCode::SUCCESS);
    ROS_INFO_NAMED("tutorial", "Visualizing plan 1 (pose goal) %s", success ? "" : "FAILED");

    if (success) {
        move_group.execute(my_plan);
    }

    ros::shutdown();
    return 0;
}

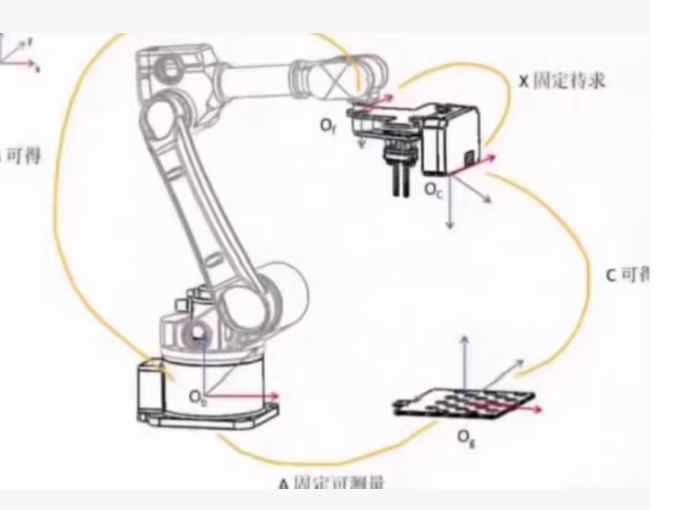
我们可以编写一个MATLAB代码来实现正运动学和逆运动学分析。假设我们已经知道每个关节的DH参数，并且我们需要计算末端执行器的位置和姿态。

步骤：

1. 定义DH参数：根据图中的坐标系定义，设置每个关节的DH参数。
2. 正运动学：使用DH参数计算末端执行器的位置和姿态。
3. 逆运动学：给定末端执行器的目标位置和姿态，求解各关节的角度。

示例代码：

% 清空工作区
clear; clc;

% 导入 Robotics Toolbox
try
    startup_rvc;
catch
    disp('Robotics Toolbox not found. Please install it first.');
end

% 定义机械臂的 DH 参数 (Denavit-Hartenberg 参数)
% 假设以下参数是根据图中坐标系定义得到的
L1 = Link([0 0.150 0 pi/2], 'sigma', 0, 'offset', 0); % 第1关节
L2 = Link([0 0 0.240 0], 'sigma', 0, 'offset', 0);    % 第2关节
L3 = Link([0 0 0.210 0], 'sigma', 0, 'offset', 0);    % 第3关节
L4 = Link([0 0.110 0 pi/2], 'sigma', 0, 'offset', 0); % 第4关节
L5 = Link([0 0 0 -pi/2], 'sigma', 0, 'offset', 0);    % 第5关节
L6 = Link([0 0.090 0 0], 'sigma', 0, 'offset', 0);    % 第6关节

% 创建机械臂模型
robot = SerialLink([L1, L2, L3, L4, L5, L6], 'name', 'SixDOF_Robot');

% 显示机械臂结构
robot.plot([0, 0, 0, 0, 0, 0]); % 默认零角度
robot.display();

%% 正运动学计算
% 输入关节角度 (单位: 弧度)
theta = [0, pi/4, pi/4, pi/6, pi/3, pi/2];

% 计算末端执行器位姿
T = robot.fkine(theta);
disp('末端执行器位姿矩阵:');
disp(T);

%% 逆运动学计算
% 目标末端执行器位姿
T_target = T; % 使用正运动学的结果作为目标

% 求解逆运动学
q_inv = robot.ikine(T_target, 'mask', [1 1 1 1 1 1]); % mask表示自由度约束
disp('逆运动学求解的关节角度:');
disp(q_inv);

%% 绘制机械臂轨迹
% 轨迹规划
t = 0:0.1:2; % 时间向量
q_traj = jtraj([0, 0, 0, 0, 0, 0], theta, t); % 从初始位置到目标位置

% 动画显示
robot.plot(q_traj);

注意事项：

• DH参数：请根据实际机械臂的规格调整上述DH参数。如果图中没有明确标注具体的尺寸和角度，请参考机械臂的说明书或CAD图纸。
• 坐标系定义：确保DH参数中的d, a, alpha与图中的坐标系定义一致。
• ROS仿真：如果您需要在ROS环境中进行仿真，可以将上述MATLAB代码生成的DH参数和运动学模型导入到URDF文件中，并使用MoveIt!进行路径规划和控制。

ROS环境下的机械臂仿真步骤：

1. 创建URDF文件：基于机械臂的CAD模型或图纸，使用urdf_tutorial包创建URDF文件。
2. 配置MoveIt!：使用moveit_setup_assistant为你的机械臂配置MoveIt!。
3. 编写控制节点：使用C++或Python编写ROS节点，利用MoveIt! API进行路径规划和控制。

我们可以编写一个MATLAB代码来实现正运动学和逆运动学分析。由于图像中没有具体的尺寸和参数信息，我们将使用假设的DH参数进行示例说明。您可以根据实际机械臂的规格调整这些参数。

示例代码：六自由度机械臂的正逆运动学

% 清空工作区
clear; clc;

% 导入 Robotics Toolbox
try
    startup_rvc;
catch
    disp('Robotics Toolbox not found. Please install it first.');
end

% 定义机械臂的 DH 参数 (Denavit-Hartenberg 参数)
% 假设以下参数是根据图中坐标系定义得到的
L1 = Link([0 0.150 0 pi/2], 'sigma', 0, 'offset', 0); % 第1关节
L2 = Link([0 0 0.240 0], 'sigma', 0, 'offset', 0);    % 第2关节
L3 = Link([0 0 0.210 0], 'sigma', 0, 'offset', 0);    % 第3关节
L4 = Link([0 0.110 0 pi/2], 'sigma', 0, 'offset', 0); % 第4关节
L5 = Link([0 0 0 -pi/2], 'sigma', 0, 'offset', 0);    % 第5关节
L6 = Link([0 0.090 0 0], 'sigma', 0, 'offset', 0);    % 第6关节

% 创建机械臂模型
robot = SerialLink([L1, L2, L3, L4, L5, L6], 'name', 'SixDOF_Robot');

% 显示机械臂结构
robot.plot([0, 0, 0, 0, 0, 0]); % 默认零角度
robot.display();

%% 正运动学计算
% 输入关节角度 (单位: 弧度)
theta = [0, pi/4, pi/4, pi/6, pi/3, pi/2];

% 计算末端执行器位姿
T = robot.fkine(theta);
disp('末端执行器位姿矩阵:');
disp(T);

%% 逆运动学计算
% 目标末端执行器位姿
T_target = T; % 使用正运动学的结果作为目标

% 求解逆运动学
q_inv = robot.ikine(T_target, 'mask', [1 1 1 1 1 1]); % mask表示自由度约束
disp('逆运动学求解的关节角度:');
disp(q_inv);

%% 绘制机械臂轨迹
% 轨迹规划
t = 0:0.1:2; % 时间向量
q_traj = jtraj([0, 0, 0, 0, 0, 0], theta, t); % 从初始位置到目标位置

% 动画显示
robot.plot(q_traj);

注意事项：

• DH参数：请根据实际机械臂的规格调整上述DH参数。如果图中没有明确标注具体的尺寸和角度，请参考机械臂的说明书或CAD图纸。
• 坐标系定义：确保DH参数中的d, a, alpha与图中的坐标系定义一致。
• ROS仿真：如果您需要在ROS环境中进行仿真，可以将上述MATLAB代码生成的DH参数和运动学模型导入到URDF文件中，并使用MoveIt!进行路径规划和控制。

ROS环境下的机械臂仿真步骤：

1. 创建URDF文件：基于机械臂的CAD模型或图纸，使用urdf_tutorial包创建URDF文件。
2. 配置MoveIt!：使用moveit_setup_assistant为你的机械臂配置MoveIt!。
3. 编写控制节点：使用C++或Python编写ROS节点，利用MoveIt! API进行路径规划和控制。