参考文章

Train With Mixed Precision
Transformer Math 101
论文：2019.02 - Adapters: Parameter-Efficient Transfer Learning for NLP
论文：2021.01 - Prefix-Tuning: Optimizing Continuous Prompts for Generation
论文：2021.04 - Prompt Tuning: The Power of Scale for Parameter-Efficient Prompt Tuning
论文：2021.05 - P-Tuning: GPT Understands, Too
论文：2021.10 - P-Tuning v2: Prompt Tuning Can Be Comparable to Fine-tuning Universally Across Scales and Tasks
论文：2021.06 - LoRA: Low-Rank Adaptation of Large Language Models
论文：2023.05 - QLoRA: Efficient Finetuning of Quantized LLMs

---

TLDR;

对于特定下游任务，人工设计prompt存在较大方差，结果往往是次优的。大模型全参数微调占用显存大、训练速度慢（梯度计算、参数更新），而且每个下游任务都需要训练一个大模型，多场景时部署困难。

高效微调的出发点是避免或缓解人工设计prompt过程、单个任务仅新增少量参数、多任务共享pretrained backbone。为此，有了以下几种微调算法：

方法	说明	微调参数量	性能水平	推理延迟	适用场景
Full Fine-tune	全参数微调	100%	100%	无	全部任务
Adapters	Self-Attn和FFN层后增加MLP层	0.1%~1%	95%以上	轻微	全部任务
Prefix-Tuning/Prompt-Tuning	输入层添加密集向量	0.01%~1%	90%以上	无	多任务NLG
P-Tuning	输入层添加多段密集向量，并使用LSTM+MLP编码	0.01%	90%以上	无	多任务NLU
P-Tuning v2	各层输入添加密集向量	0.05%~2%	95%以上	轻微	多任务NLU
LoRA	选择部分参数矩阵，添加两个低秩旁路矩阵	0.01%~0.1%	95%以上	无	全部任务

---

基础知识

FP32 (Single-precision floating-point, 单精度浮点数)

IEEE 754标准的单精度浮点数使用1位符号位、8位指数位和23位尾数位，表示如下：

二进制转十进制浮点数的转换公式：
$$(-1{)}^{b_{31}}\times 2^{(b_{30}\cdots b_{23}{)}_2-127}\times (1.b_{22}\cdots b_0{)}_2=(-1{)}^s\times 2^{E-127}\times \left(1+\sum _{i=0}^{22}{b}_{22-i}{2}^{-i-1}\right)$$

32位有符号整数最大数值为$2^{31}-1=2147483647$，32位基为2的单精度浮点数最大数值为$(-1{)}^0\times 2^{254-127}\times (1+1-2^{-23})\approx 3.4028235\times 10^{38}$。指数位取值范围是1~254，全0和全1用于表示特殊数字，比如inf和nan等。

上图中浮点数为$(-1{)}^0\times 2^{124-127}\times (1+2^{-2})=1/8\times 5/4=0.15625$。

单精度浮点数不同指数取值下的数值间隔/精度
浮点数比定点数能够表示范围更高的数值，但会损失一定精度。IEEE 754约定了数值转换精度，6位有效数字的十进制数转为单精度浮点数，可无损转回到原十进制数；9位有限数字的单精度浮点数转为十进制数，可无损转回原单精度浮点数。

数值精度：7位有效数字
对于指数位为150的情况，最小数值为8388608，间隔为1，也就是说可以精确表示8388609，无法表示8388608.5。也就是说，可以精确表示该区间内7位有效数字的数，无法表示的数值会自动舍入到可最近表示的数值。

对于1024~12048之间的数，查表可知间隔为0.00012207，只能精确表示3位小数，比如无法存储1024.0005。

FP16 (Half-precision floating-point, 半精度浮点数)

IEEE 754标准的单精度浮点数使用1位符号位、5位指数位和10位尾数位，表示如下：

16位基为2的单精度浮点数的最大数值为$-1^0\times 2^{30-15}\times (1+1-2^{-10})=65504$，最小正数为$-1^0\times 2^{1-15\times 1}=2^{-14}\approx 6.10\times 10^{-5}$。

单精度在部分数值区间的表示精度

数值精度：3～4位有效数字
对于0.25到0.5区间，间隔为0.000244，能精确表示到0.001，4位有效数字。对于2048到4096区间，间隔位2，能精确表示到10分位，3位有效数字。

BF16 (Brain floating-point)

使用1位符号位，8位指数位，7位尾数位。数值动态范围与FP32一致，相互之间转换快。FP32把后16位尾数截断就可以转为BF16；BF16扩展到32位，低位补0就可以转为FP32。

混合精度训练显存分析

GPU具有高带宽、高并行特点，GPU与显存之间的数据读写、转换速度受显存带宽限制。低精度数据显存占用少，带宽需求低，可加速数据转换操作。Volta和Turing架构的低精度Tensor Core，算力也更高。混合精度训练可在需要高精度的运算中使用高精度计算，其他地方使用低精度计算。

A100算力：A100 80GB PCIe GPU的FP32 CUDA Core算力是19.5TFLOPS，而FP16 Tensor Core算力是312TFLOPS。A100 SXM的Tensor Core算力还要比PCIe再高一倍。

CUDA Core vs Tensor Core： CUDA Core是GPU通用计算单元，可灵活执行图形渲染、常规数学计算，并行处理小任务。Tensor Core专用于深度学习，高吞吐，可在单时钟内完成多次混合/低精度矩阵运算（乘法和加法），协作处理大矩阵运算。

训练过程中包含静态显存和动态显存。静态显存主要是模型参数、梯度和优化器状态，动态显存是激活显存。

静态显存分析
不同类型半精度训练的差异，原文在这里。 FP16精度训练，梯度以FP16存储，backward时要缩放loss以避免梯度数值溢出，更新梯度时转为FP32。BF16精度训练，梯度以FP32存储，不需要转换。

对于参数量为$\Phi$的模型，使用Adam优化器，混合精度训练。使用FP16+FP32混合精度单卡训练，FP16参数$2\Phi$，FP32参数副本$4\Phi$，FP16梯度$2\Phi$，FP32梯度副本$4\Phi$，优化器一二阶状态$8\Phi$，总计$20\Phi$。若使用BF16，梯度直接以FP32存储，总计$18\Phi$。

训练过程中计算loss后，一般会执行loss.float()把loss转为FP32，不会影响内部参数的梯度精度！

分布式混合精度训练：FP16精度下，DDP模式与单卡一致；ZeRO1分割$8\Phi$优化器状态，以及$4\Phi$参数副本和$4\Phi$梯度副本；ZeRO2分割$2\Phi$的梯度；ZeRO3分割$2\Phi$的参数。BF16精度下，因梯度存储、更新方式不一致，有所区别。详见下表。

动态显存分析
LLMs训练时激活显存受批次大小、序列长度和模型架构影响。对于标准单层Transformer Layer，若输入长度为$s$，隐藏层大小为$d$，注意力头数为$a$，无dropout，则激活显存：注意力输入QKV为3sd、QK注意力分数+权重为2ass、注意力输出+输出变换为2sd、MLP上采样+激活+下采样为9sd、2层归一化为2sd，总计16sd+2ass。

若批次大小$b$为2、序列长度$s$为1024、精度为BF16，对于0.6B的Qwen3模型（隐藏层大小$d$为1024、网络层数$l$为28、注意力头数$a$为16），不考虑输入输出embedding层、QK的Norm，总激活显存为2bl(16sd+2ass)=5.25Gb。

这篇论文考虑dropout，半精度激活显存是2bl(17sd + 2.5ass)，0.5是考虑bool型的attention_mask。

现在训练大模型大多开启Activation checkpointing/recomputation，forward时不保存中间激活值，backward时重新计算。backward计算量大约是forward的2倍，重新执行forward算力约损失33.3%。

前后向计算量分析
输入$x$，标签$y$，$z$为线性变化输出，$a$为非线性激活值，两层神经网络：
$$z_1=w_{1}x+b_1,a_1=\sigma (z_1),z_2=w_2{z}_1+b_2,a_2=\sigma (z_2)⟹\mathcal{L}(a_2,y)$$
梯度更新，对损失函数$\mathcal{L}(a_2,y)$链式求导：
$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial w_2}& =\frac{\partial \mathcal{L}}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}={\delta }_2\cdot \frac{\partial z_2}{\partial w_2}={\delta }_2\cdot z_1\\ & \\ \frac{\partial \mathcal{L}}{\partial w_1}& ={\delta }_2\cdot \frac{\partial z_2}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}={\delta }_1\cdot \frac{\partial z_1}{\partial w_1}={\delta }_1\cdot x\end{array}$$
从后向过程的链式求导来看，计算量与前向过程一致，但还需要考虑梯度计算的计算量，因此大致是2倍。

高效训练参数

内容来自于：Hugging Face: Efficient Training on a Single GPU。

• Batch Size 批次大小影响显存占用和训练速度。大批次可充分利用GPU并行算力，通常设置为2的N次方。如果使用Tensor Core，批次大小取决于GPU型号和数据精度。如FP16训练，通常设置为8的倍数，A100则设置为64的倍数。
• Gradient Accumulation 累积多个mini-batch的梯度更新模型，用于需要使用大批次更新参数，但受显存限制，单次不能使用大批次的情况。需要累加梯度，训练速度略降。
• Gradient Checkpointing 仅存储forward中的少部分激活，backward时重新计算，避免存储所有中间激活状态，以降低激活显存，增加了额外计算量（33%），训练速度约降低20%。
• Mixed Precision 部分计算使用FP16/BF16，其他计算使用FP32，权衡速度和精度。半精度计算成本低，GPU的半精度算力通常比单精度高得多。参数优化时需要将FP16梯度转为FP32梯度，并且需要额外的FP32模型副本，对于小批次（不考虑Gradient Checkpoint）会占用更多显存。
• Optimizers 默认使用Adam优化器，Adam需要存储梯度的历史状态（一二阶动量），占大量显存。有一些高效实现，比如NVIDIA的adam_apex_fused、8-bit AdamW等。
• Data preloading 在GPU计算时，CPU同步加载数据。可通过为CPU分配pinned memory存储数据，并直接转换到GPU，或者使用多进程CPU预加载数据。
• torch.empty_cache_steps 训练过程中释放训练未用的GPU缓存，避免OOM，但训练速度大约下降10%。
• torch.compile 把pytorch代码编译为优化的kernel，提升训练速度。

高效微调方法

为什么要进行高效/部分参数微调？ LLMs zeroshot或者fewshot无法获取较好效果；LLMs对prompt敏感，人工设计的prompt通常是次优的；全参数微调代价高，并且多个下游任务无法共用一个基座模型。

Adapters: Parameter-Efficient Transfer Learning for NLP

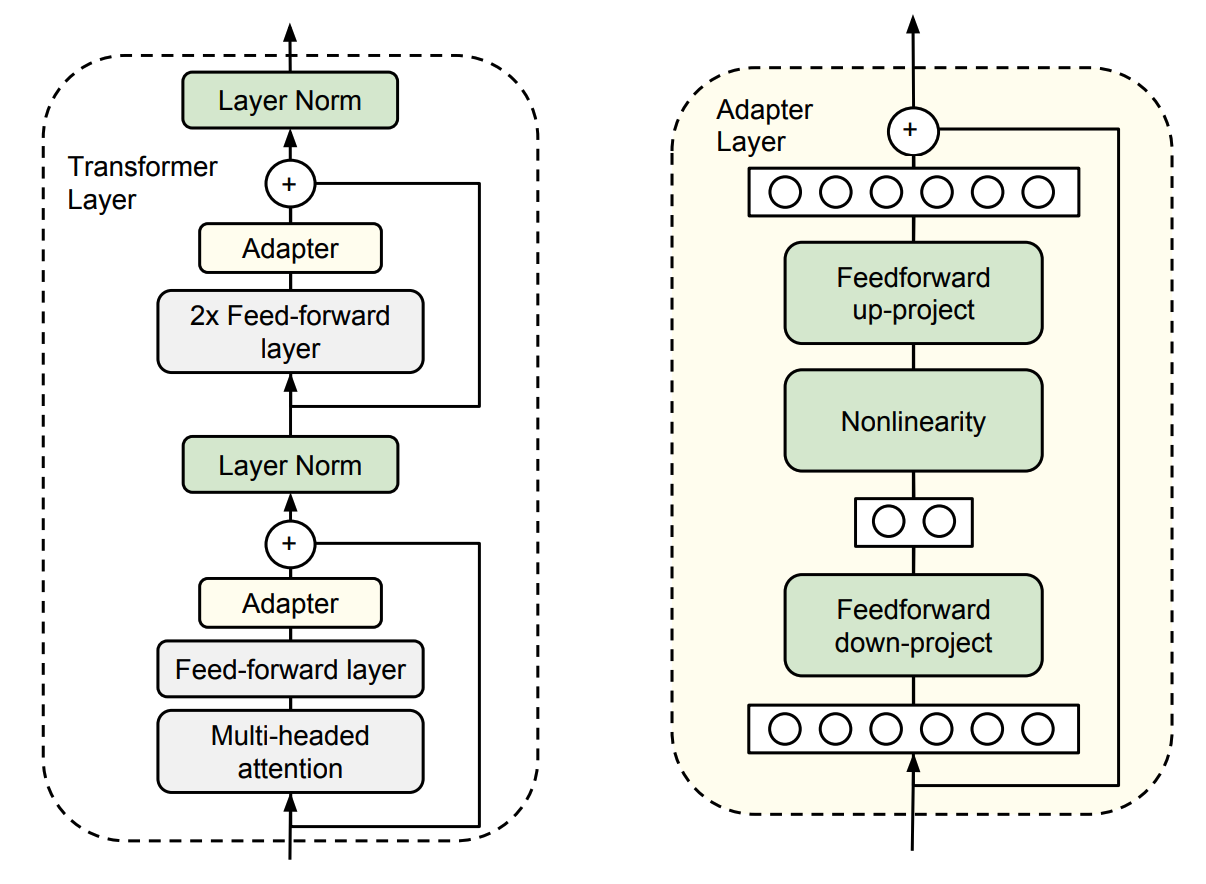
在原始Transformer Layer的Self-Attn层和FFN层之后分别添加一个FFN层，下游任务微调时冻结原模型参数，只调整新增Adapters层的参数。

模型隐藏层为$d$，Adapters隐藏层大小为$m$，则新增参数量为$2md+m+d$。新增FFN的隐藏层大小$m\ll d$，以控制整个网络新增的参数量，大约是原模型参数的$0.3-8\%$。新增FFN的输入和输出之间使用residual，若初始化参数接近0，如0均值小方差，则初始微调时不影响原网络输出。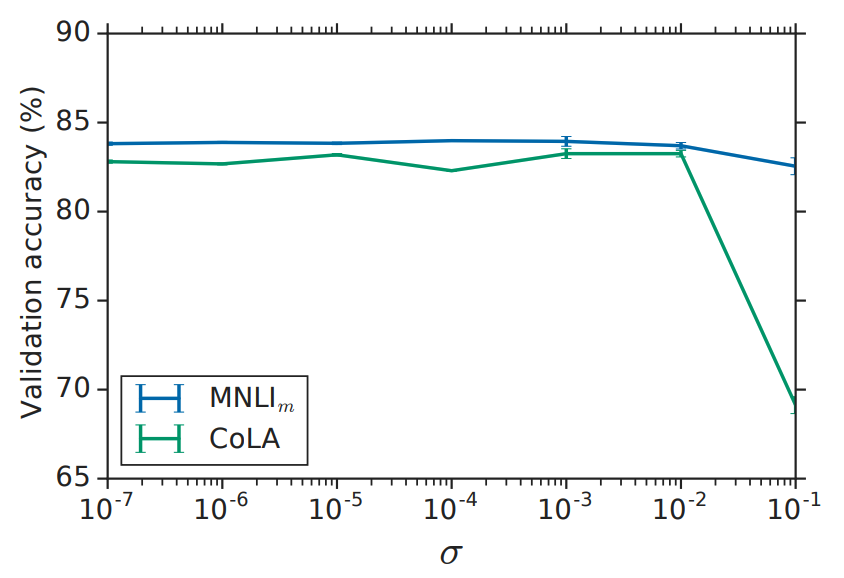

Adapter参数不同初始化方差对性能的影响

---

Prefix-Tuning: Optimizing Continuous Prompts for Generation

适用于NLG微调：GPT自回归模型，输入构造为【PREFIX; x; y】；T5编解码模型，输入构造为【PREFIX; x; PREFIX’; y】。PREFIX是提示密集向量，为保证训练稳定性，PREFIX密集向量还会经过一层MLP，最终新增参数仅为0.1%。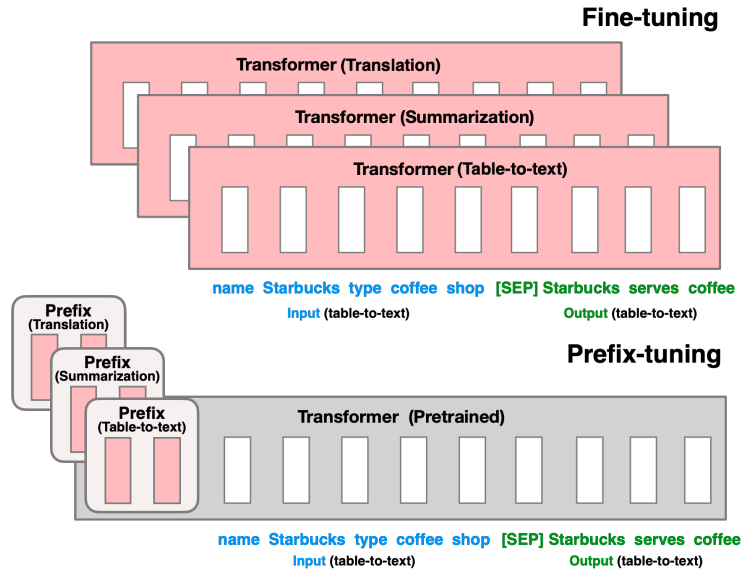

该方法与Prompt-tuning方法基本一致，更多细节可查阅下面的Prompt Tuning章节。

---

Prompt Tuning: The Power of Scale for Parameter-Efficient Prompt Tuning

与Prefix-tuning思想相近，只比Prefix-tuning少了一层MLP。

Prompt-tuning是在输入序列前添加一些额外token，作为“soft prompt”，来适配下游任务的方法。具体来说，在每个任务的输入序列前加上$k$个可调整权重的token（称为“soft prompt”），这可视作为在输入序列前加入一些特殊token，再去生成目标文本。训练时，冻结预训练模型参数。端到端训练后，加入的token embedding压缩了整个标注数据集的信号，可以同时适配多个下游任务，最终效果好于few-shots，逼近全参数微调。

输入文本（分词后长度为$n$）的嵌入表示为$X_e\in {\mathbb{R}}^{n\times e}$，对于特定任务，我们在输入嵌入前扩展大小为${\mathbb{R}}^{p\times e}$的密集嵌入$P_e$，最终输入为$[P_e;X_e]\in {\mathbb{R}}^{(p+n)\times e}$。具体初始化、拼接代码如下：

# __init__
# 可以设计一个简单的prompt，通过word_embedding编码作为初始参数。
self.prompt_embedding = torch.nn.Parameter(torch.randn(prompt_length, hidden_size))

# forward
batch_size, seq_len, hidden_size = inputs_embeds.size()
# 假设微调单个任务
prompt_embeds = self.prompt_embedding.unsqueeze(0).expand(batch_size, -1, -1)
inputs_embeds = torch.cat((prompt_embeds, inputs_embeds), dim=1)
# 调整attn_mask
...

---

P-Tuning: GPT Understands, Too

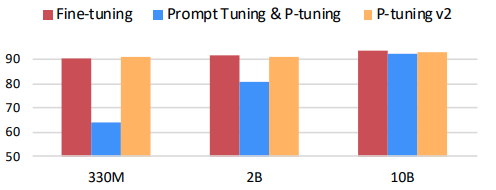
P-Tuning是一种将GPT簇模型应用到NLU任务的方法，人工设计prompt方差大，性能次优。在NLU任务上Fine-tune预训练模型，BERT的效果明显优于GPT。若使用P-Tuning方法，SuperGLUE任务上两簇模型效果均得到提升，GPT簇模型提升更加显著，最终效果优于BERT Fine-tune。

P-Tuning将输入模板中prompt的离散token换成密集向量，微调过程可视为在连续空间中搜索prmpt，而prompt-engineering是在离散空间中人工设计prompt。具体做法是，在输入序列中前后两端插入prompt密集向量（插入位置和数量可调），输入序列变为：
{ h 0 , . . . , h i , e ( x ) , h i + 1 , ⋯   , h m , e ( y ) } \{h_0,...,h_i,\bm e(\bm x), h_{i+1}, \cdots, h_{m}, \bm e(\bm y)\} {h0​,...,hi​,e(x),hi+1​,⋯,hm​,e(y)}

其中${\mathbf{h}}_{0:i}$和${\mathbf{h}}_{i+1:m}$是两段prompt密集向量。

下图(a)中prompt使用固定离散的标记，图(b)使用随机初始化的密集向量。训练过程中[MASK]替换为真值。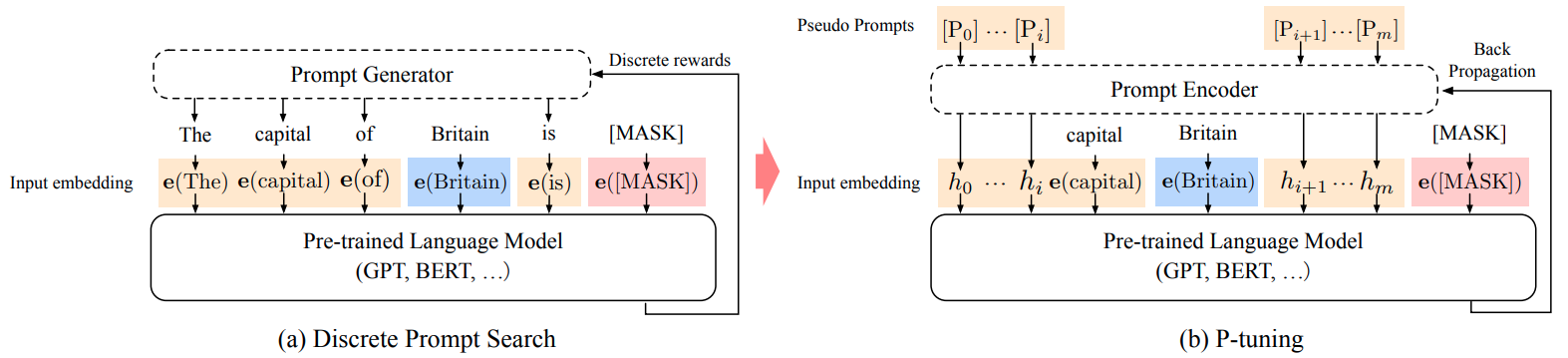

为增加prompt tokens之间的内在关联性，我们通过prompt编码器（LSTM和MLP层）对prompt向量编码。此外，在模板中加入一些锚点可以进一步增加P-Tuning的性能，比如RTE任务中在[HYP]后添加?，充当询问部分。

---

P-Tuning v2: Prompt Tuning Can Be Comparable to Finetuning Universally Across Scales and Tasks

P-Tuning v2出发点是改善P-Tuning在小模型和序列任务上表现不佳的问题。该方法在每一层网络输入前添加prompt嵌入，可视为prefix-tuning方法在NLU任务上的优化版本。作为 “deep prompt tuning” 方法，在小模型和复杂任务上也有不错的表现。

在每层网络前添加PREFIX向量，适用于分类、序列标注等NLU任务。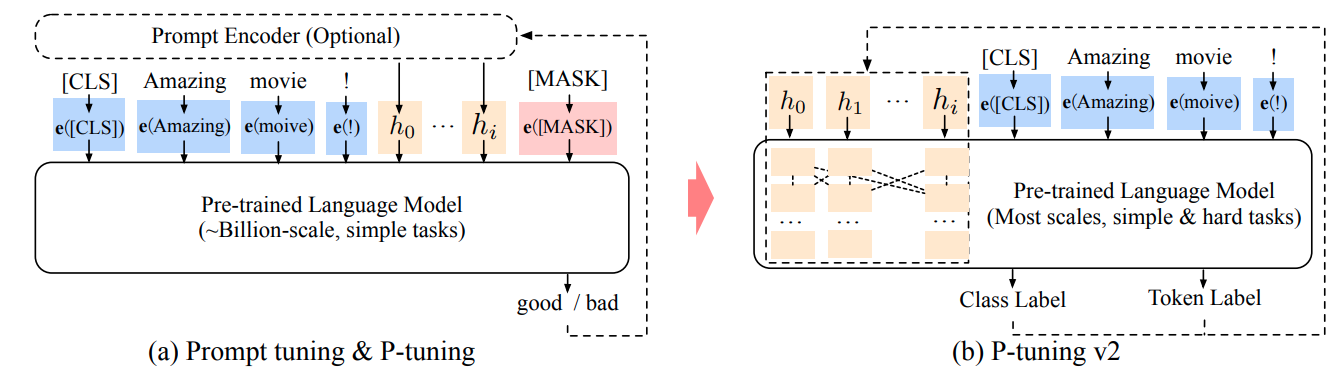

新增大约0.1%至3%的参数。

---

LoRA: Low-Rank Adaptation of Large Language Models

训练好的模型参数通常是低秩矩阵。假设微调下游任务时，参数更新矩阵也是低秩矩阵，则更新过程等价于：
$$h=W_{0}x+\Delta Wx=W_{0}x+BAx$$

其中参数更新矩阵$\Delta W$可表示为两个低秩矩阵相乘，其中$A\in {\mathbb{R}}^{r\times d}$，$B\in {\mathbb{R}}^{d\times r}$，$r\ll n$。训练过程中固定原参数，至更新两个低秩矩阵。

若$\gamma$表示应用LoRA的参数比例，全参数微调的参数更新量为$d^2$，使用Lora微调的参数更新量为$\gamma 2dr$，大约是$2\gamma r/d$。

LoRA算法参数：

• r：秩的数值。
• alpha：BA矩阵乘的缩放系数，数值大小影响训练速度和稳定性，配合学习率使用，一般去4r。
• dropout：LoRA输入的概率裁剪值；

---

QLoRA: Efficient Finetuning of Quantized LLMs

相比LoRA的区别：使用NF4量化权重；对量化常数再量化；分页管理优化器显存峰值。

为何使用NF4量化权重？
QLoRA认为权重基于正太分布初始化，训练好的参数也服从正太分布。也就是说，大量权重分布与均值附近，使用均匀量化会导致大量权重被压缩到较窄的量化区间。NF4（4-bit Normal Float）通过分位数量化（Quantile Quantization）存储服从正太分布的权重，是信息论最优的存储。NF4属于非均匀、对称量化方法。

怎么使用NF4量化权重？
需要将分位数和权重都缩放到[-1, 1]区间。

17分位数缩放到[-1, 1]区间。 权重使用absmax缩放，属于对称量化，无法精确表示零点。零点在深度学习中（填充和稀疏表示）有重要作用，为此，NF4将[-1, 0]区间分成7段，[0, 1]区间分成8段，共计16个分位点。我们需要找到左侧面积等于右侧面积的分位数，可以从一个偏移量开始查找。NF4使用左右不对称分位，偏移量为(1-1/(2*15) + 1-1/(2*16))/2=0.9677083。详见：quantile quantization #94。

正太分布[-1, 1]内的17等分位点（16段）如下，与bitsandbytes.functional.bitandyutes.get_4bit_type中预定义的一致。

import numpy as np
import scipy.stats

offset = 0.9677083
edges = np.linspace(0.5, offset, 9)
norm_values = scipy.stats.norm.ppf(edges)
v2 = norm_values / norm_values.max()

edges = np.linspace(offset, 0.5, 8)
norm_values = scipy.stats.norm.ppf(edges)
v1 = norm_values / -norm_values.max()

v = v1.round(6).tolist()[:-1] + [0] + v2.round(6).tolist()[1:]

[-1, 1]分位量化的16个点位：

[-1.0, -0.696193, -0.525073, -0.394917, -0.284441, -0.184773, -0.09105, 0, 
  0.07958, 0.16093, 0.246112, 0.337915, 0.44071, 0.562617, 0.722957, 1.0]

权重缩放到[-1, 1]区间并执行分位量化。 根据block-size划分组，计算每组权重的absmax值，缩放到[-1, 1]区间，取最近邻分位点的索引作为量化数值。反量化时，取量化数值对应的分位点，乘以所在组的absmax即可。

bitsandbytes使用c实现，源码不可见，py复现版本如下：

from typing import Tuple

import torch
from bitsandbytes.functional import dequantize_nf4, get_4bit_type, quantize_nf4

# 正态分布[-1,1]内的16个分位点，用于4进制分位量化。
QUANTILES = get_4bit_type('nf4', device='cpu')


def fp32_to_nf4(w: torch.Tensor, blocksize=64):
    absmax = w.view(-1, blocksize).abs().max(1, keepdim=True).values
    a = w.view(-1, blocksize) / absmax.float()
    diff = a.unsqueeze(-1) - QUANTILES.view(1, -1)
    out = diff.abs().argmin(-1)
    out = out.view(-1, 2)
    out = ((out[:, 0] << 4) + out[:, 1]).to(torch.uint8)
    return out, absmax, w.shape


def nf4_to_fp32(w: torch.Tensor, absmax: torch.Tensor, shape: Tuple[int, ...], blocksize: int):
    w = w.view(-1)
    assert blocksize == 2 * w.numel() // absmax.numel()
    out = torch.stack((w >> 4, w & 0x0F), 1).view(-1).to(torch.int32)
    out = QUANTILES[out].view(-1, blocksize)
    out = out * absmax.view(-1, 1)
    out = out.view(*shape).float()
    return out


if __name__ == '__main__':
    torch.manual_seed(1234)
    sigma = 0.1
    w0 = torch.randn((1024, 4096), dtype=torch.float32) * sigma
    blocksize = 64
    out, absmax, shape = fp32_to_nf4(w0, blocksize)
    w1 = nf4_to_fp32(out, absmax, shape, blocksize)

    print('\n\nOrigin Weight:\n', w0)
    print('\n\nQuant-Dequant Weight:\n', w1)

    out, state = quantize_nf4(w0.cuda(), blocksize=blocksize, )
    w2 = dequantize_nf4(out, state)
    print('\n\nQuant-Dequant Weight In BNB:\n', w2)

Origin Weight:
 tensor([[-0.0112, -0.0497,  0.0163,  ..., -0.0897, -0.2172, -0.0275],
        [-0.0399, -0.2378, -0.0214,  ...,  0.1027,  0.0515,  0.0291],
        [ 0.1195, -0.1546, -0.1371,  ...,  0.0308, -0.2074, -0.0901],
        ...,
        [-0.1053,  0.0842, -0.0432,  ...,  0.0388,  0.0810, -0.1221],
        [ 0.0156,  0.1027,  0.1449,  ...,  0.0167,  0.0208,  0.0495],
        [ 0.0437,  0.0561, -0.0503,  ...,  0.0036, -0.0129, -0.0376]])


Quant-Dequant Weight:
 tensor([[-0.0199, -0.0403,  0.0174,  ..., -0.0916, -0.2241, -0.0293],
        [-0.0439, -0.2378, -0.0217,  ...,  0.0923,  0.0604,  0.0298],
        [ 0.1059, -0.1673, -0.1262,  ...,  0.0262, -0.2296, -0.0938],
        ...,
        [-0.1031,  0.0882, -0.0482,  ...,  0.0429,  0.0901, -0.1053],
        [ 0.0210,  0.0892,  0.1486,  ...,  0.0233,  0.0233,  0.0471],
        [ 0.0359,  0.0549, -0.0412,  ...,  0.0000, -0.0234, -0.0475]])


Quant-Dequant Weight In BNB:
 tensor([[-0.0199, -0.0403,  0.0174,  ..., -0.0916, -0.2241, -0.0293],
        [-0.0439, -0.2378, -0.0217,  ...,  0.0923,  0.0604,  0.0298],
        [ 0.1059, -0.1673, -0.1262,  ...,  0.0262, -0.2296, -0.0938],
        ...,
        [-0.1031,  0.0882, -0.0482,  ...,  0.0429,  0.0901, -0.1053],
        [ 0.0210,  0.0892,  0.1486,  ...,  0.0233,  0.0233,  0.0471],
        [ 0.0359,  0.0549, -0.0412,  ...,  0.0000, -0.0234, -0.0475]],
       device='cuda:0')

为何要对量化参数二次量化？
考虑blocksize=64量化，反量化所需的absmax使用32位存储，因此每个参数需要4+32/64=4.5bit。如果将absmax使用blocksize=256量化到8bit，则每个参数量化后只需要4+(8+32/256)/64=4.127bit。

Paged Optimizers
NVIDIA允许GPU和CPU之间数据page-to-page交换，QLoRA在显存OOM时，将优化器状态移到CPU内存，需要更新优化器状态时再移到GPU显存。这一过程很像deepspeed中的optimizer cpu offload技术。