微环谐振腔的光学频率梳matlab仿真 微腔光频梳仿真 包括求解LLE方程（Lugiato-Lefever equation）实现微环中的光频梳，同时考虑了色散，克尔非线性，外部泵浦等因素，具有可延展性。 已实现论文复现，不加热效应的原始LLE方程也有。

在光学领域，微环谐振腔的光学频率梳研究一直是个热门方向。今天就来聊聊基于Matlab对微腔光频梳进行仿真的那些事儿。

核心：求解LLE方程

我们的关键任务之一是求解Lugiato - Lefever equation（LLE方程），以此来实现微环中的光频梳。这个方程可不简单，它综合考虑了诸多重要因素，像色散、克尔非线性以及外部泵浦等等，正是这些因素让微环中的光频梳现象得以呈现，而且基于此方程的仿真还具备可延展性，这意味着后续可以进一步拓展研究内容。

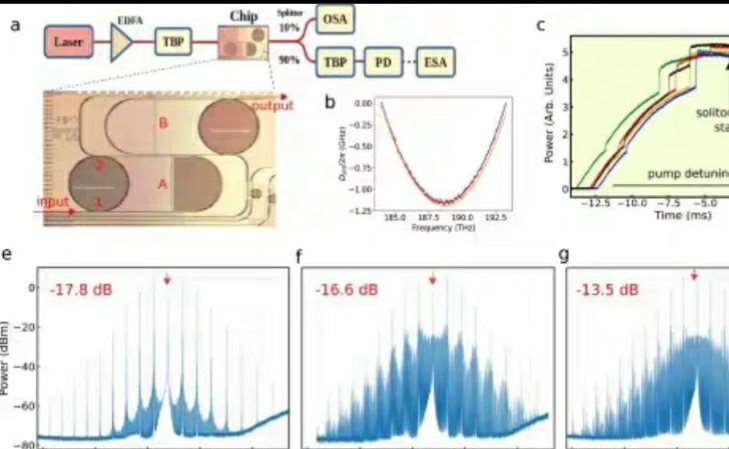
下面简单展示一下求解LLE方程在Matlab中的代码框架（为简化理解，仅呈现关键部分）：

% 参数设定
lambda0 = 1550e - 9; % 中心波长
omega0 = 2 * pi * physconst('LightSpeed') / lambda0; % 中心角频率
gamma = 1e9; % 克尔非线性系数
beta2 = - 20e - 24; % 二阶色散系数
kappa = 1e6; % 腔损耗率
Pp = 1e - 3; % 泵浦功率

% 空间和时间离散化
N = 1024; % 空间点数
T = 1e - 6; % 总时间
dt = 1e - 12; % 时间步长
dz = 1e - 6; % 空间步长

z = (0:N - 1) * dz;
t = (0:dt:T - dt);

% 初始化场
E = zeros(N, length(t));
E(:, 1) = sqrt(Pp) * exp(1i * omega0 * t(1));

% 迭代求解LLE方程
for n = 1:length(t) - 1
    E_temp = E(:, n);
    dE_dt = - 1i * (beta2 / 2) * diff(E_temp, 2) / dz ^ 2 - 1i * gamma * abs(E_temp). ^ 2 * E_temp - 1i * kappa * E_temp;
    E(:, n + 1) = E_temp + dE_dt * dt;
end

在这段代码里，首先我们设定了一系列的参数，像中心波长lambda0，它决定了我们研究的光频梳所在的大致频段，通过中心波长算出中心角频率omega0。克尔非线性系数gamma体现了光与物质相互作用时的非线性特性，二阶色散系数beta2影响着光在传播过程中的色散效应，腔损耗率kappa表示光在微环中传播时能量的损耗情况，泵浦功率Pp则是为微环中的光频梳提供能量输入。

接着对空间和时间进行离散化处理，确定了空间点数N和总时间T以及时间步长dt和空间步长dz，这是数值求解方程的基础。初始化场E，假设在初始时刻有一个带有泵浦功率的光场。然后通过迭代来求解LLE方程，在每一步迭代中，计算场关于时间的变化率dEdt，这里面包含了色散项（- 1i (beta2 / 2) diff(Etemp, 2) / dz ^ 2），它考虑了二阶色散对光场的影响；克尔非线性项（- 1i gamma abs(Etemp). ^ 2 Etemp），体现了光强对光场的非线性作用；以及腔损耗项（- 1i kappa * E_temp）。最后根据这个变化率更新光场E。

论文复现与原始LLE方程

值得一提的是，目前已经实现了相关论文的复现。而且在不考虑加热效应的情况下，原始的LLE方程也已具备。不考虑加热效应简化了模型，让我们能更专注于色散、克尔非线性和外部泵浦等关键因素对光频梳的影响。在实际仿真中，这种简化可以帮助我们快速理解和验证基本原理，之后再逐步添加复杂因素进行深入研究。

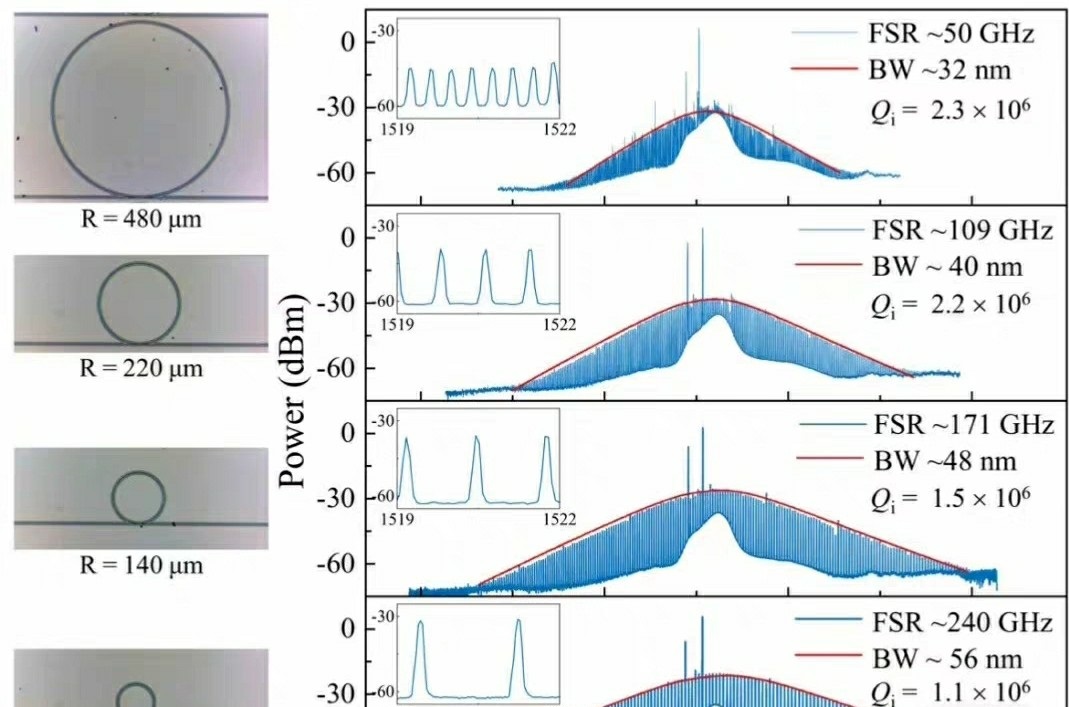
通过Matlab对微环谐振腔的光学频率梳进行仿真，基于LLE方程的求解，综合考虑多种因素，不仅实现了论文复现，还为后续进一步探索光频梳的特性和应用奠定了基础。无论是在基础光学研究还是未来光通信等应用领域，这都有着重要的意义。希望感兴趣的小伙伴们可以一起深入研究，挖掘更多有趣的现象和潜在应用。