激活函数(使模型非线性,更真实接近现实生活)
激活函数公式/规则输出范围主要用途优点缺点Sigmoid(0, 1)输出层(二分类)输出为概率梯度消失,非零中心Tanh(-1, 1)隐藏层(尤其是RNN)零中心,梯度比Sigmoid大梯度消失ReLUmax(0, x)[0, +∞)隐藏层(默认首选)计算快,缓解梯度消失神经元死亡Leaky ReLUmax(αx, x)(-∞, +∞)隐藏层(ReLU替代)解决神经元死亡问题效果不一定总优于ReL
一句话概括
激活函数是神经网络中每个神经元上的一个“开关”或“过滤器”,它决定了这个神经元是否应该被“激活”(即向下一个层传递多强的信号)。
如果没有激活函数,神经网络无论多深,都只能等价于一个简单的线性回归模型,无法学习复杂的模式和特征。
为什么需要激活函数?—— 核心作用
-
引入非线性
-
这是最根本的作用。 现实世界的数据(如图像、语言、声音)都是高度非线性的。如果没有激活函数,神经网络的每一层都只是线性变换(加权求和),那么整个网络堆叠起来依然是一个巨大的线性模型,无法拟合复杂函数。
-
比喻: 就像你用乐高积木,如果只有一种形状的积木(线性),你只能搭出简单的墙。但有了各种弯曲、转角的积木(非线性),你才能搭出城堡、飞船等复杂结构。激活函数就是给神经网络提供了“非线性积木”。
-
-
决定神经元是否激活
-
激活函数对输入信号进行转换,决定输出信号的强度。例如,有些函数像“开关”(阶跃函数),要么全有要么全无;有些则像“水龙头”(Sigmoid, Tanh),可以调节流量大小。
-
常见的激活函数及其特性
下图直观地展示了四种主要激活函数及其输出范围,帮助你快速比较它们的核心差异:
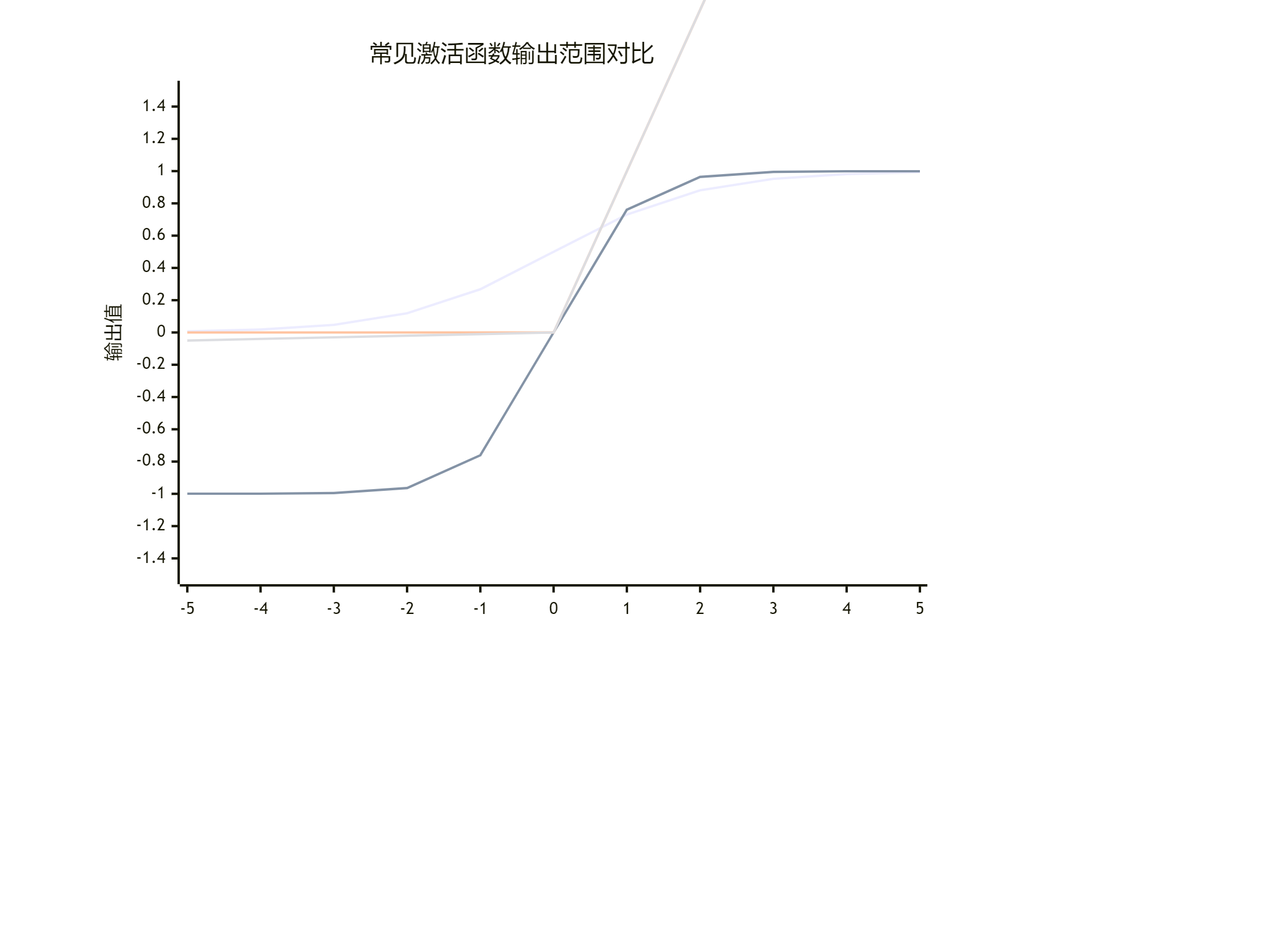
下面我们来详细看看它们的公式、特点和应用场景。
1. Sigmoid(S型函数)
-
公式:
f(x) = 1 / (1 + e^(-x)) -
特点: 将输入压缩到 (0, 1) 之间。曲线平滑,易于求导。
-
优点: 输出可以理解为概率,非常适用于二分类问题的输出层。
-
缺点:
-
梯度消失: 当输入值非常大或非常小时,函数的梯度(导数)接近于0。在反向传播时,梯度会不断相乘,导致梯度越来越小,使得网络深层的权重几乎无法更新。
-
输出非零中心: 输出恒为正,这会导致梯度更新时出现“之”字形下降,影响训练效率。
-
-
现状: 现在很少用于隐藏层,主要用在二分类的输出层。
2. Tanh(双曲正切函数)
-
公式:
f(x) = (e^x - e^(-x)) / (e^x + e^(-x)) -
特点: 将输入压缩到 (-1, 1) 之间。可以看作是Sigmoid的缩放版。
-
优点: 输出是零中心的,其收敛速度通常比Sigmoid快。
-
缺点: 同样存在梯度消失问题。
-
应用: 在自然语言处理等任务中,Tanh比Sigmoid更受欢迎,因为它具有零中心特性。
3. ReLU(整流线性单元)—— 当前最主流、默认的选择
-
公式:
f(x) = max(0, x) -
特点: 输入为正时,输出等于输入;输入为负时,输出为0。
-
优点:
-
计算极其简单,大大加快了训练速度。
-
缓解梯度消失: 在正区间,梯度恒为1,有效解决了梯度消失问题。
-
-
缺点:
-
Dying ReLU(神经元死亡): 一旦输入落入负区间,梯度为0,该神经元可能永远无法被再次激活,相应的权重也无法更新。
-
-
应用: 是绝大多数卷积神经网络和深度前馈网络的隐藏层标配。
4. Leaky ReLU(带泄露的ReLU)—— ReLU的改进版
-
公式:
f(x) = max(αx, x)(其中α是一个很小的常数,如0.01) -
特点: 当输入为负时,不再直接输出0,而是输出一个很小的斜率值(αx)。
-
优点: 解决了“Dying ReLU”问题,给负区间一个微小的梯度,使得神经元有机会被修复。
-
应用: 当担心出现大量“死亡神经元”时,可以作为ReLU的替代品。
5. Softmax函数
-
特点: 它将多个神经元的输出(通常是输出层)压缩到 (0, 1) 之间,并且所有输出值的和为1。
-
优点: 输出结果可以直接解释为概率分布。例如,一个10分类问题的输出层有10个神经元,Softmax会计算出输入样本属于这10个类别中每一个的概率。
-
应用: 专门用于多分类问题的输出层。
如何选择激活函数?
虽然选择没有绝对规则,但有以下通用指南:
-
隐藏层:
-
首选ReLU: 因为它计算简单、效果好,是大多数情况的默认选择。
-
如果担心“神经元死亡”,可以尝试 Leaky ReLU 或其变体(如PReLU)。
-
在RNN等网络中,Tanh 有时仍有应用。
-
-
输出层:
-
二分类问题: 用 Sigmoid,输出可以理解为正类的概率。
-
多分类问题: 用 Softmax,输出每个类别的概率。
-
回归问题(如预测房价): 通常不使用激活函数(或称使用线性激活函数),直接输出任意实数。
-
总结
| 激活函数 | 公式/规则 | 输出范围 | 主要用途 | 优点 | 缺点 |
|---|---|---|---|---|---|
| Sigmoid | 1 / (1 + e^(-x)) |
(0, 1) | 输出层(二分类) | 输出为概率 | 梯度消失,非零中心 |
| Tanh | (e^x - e^(-x)) / (e^x + e^(-x)) |
(-1, 1) | 隐藏层(尤其是RNN) | 零中心,梯度比Sigmoid大 | 梯度消失 |
| ReLU | max(0, x) |
[0, +∞) | 隐藏层(默认首选) | 计算快,缓解梯度消失 | 神经元死亡 |
| Leaky ReLU | max(αx, x) |
(-∞, +∞) | 隐藏层(ReLU替代) | 解决神经元死亡问题 | 效果不一定总优于ReLU |
| Softmax | e^z_i / ∑(e^z_j) |
(0, 1) 且和为1 | 输出层(多分类) | 输出为概率分布 | 仅用于输出层 |
简单记住:隐藏层用ReLU,分类输出层用Sigmoid或Softmax,你就已经掌握了90%的应用场景。

火山引擎开发者社区是火山引擎打造的AI技术生态平台,聚焦Agent与大模型开发,提供豆包系列模型(图像/视频/视觉)、智能分析与会话工具,并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长,新用户可领50万Tokens权益,助力构建智能应用。
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容





所有评论(0)