1. 一段话总结

为解决Latent Diffusion Models (LDMs)（如Stable Diffusion）生成高分辨率图像时迭代采样计算密集、速度慢的问题，研究人员借鉴Consistency Models提出Latent Consistency Models (LCMs)；LCMs在图像潜在空间直接预测增强概率流ODE（PF-ODE）的解，通过一步引导蒸馏方法（融合Classifier-Free Guidance, CFG）和SKIPPING-STEP技术（k=20，将时间步从千级缩短至几十级）加速收敛，仅需32 A100 GPU小时即可训练出支持2∼4步生成768×768高分辨率图像的模型；同时提出Latent Consistency Fine-tuning (LCF) 适配定制数据集，在LAION-5B-Aesthetics数据集上，LCMs在1∼4步推理下的FID和CLIP分数均超越DDIM、DPM、Guided-Distill等基线，实现少步推理的SOTA性能。

---

2. 思维导图（mindmap）

## 一、研究背景与动机
- 1. 现有模型局限
  - LDMs（如Stable Diffusion）：高分辨率但迭代采样慢
  - Consistency Models：仅像素空间，不支持高分辨率/文本生成
- 2. 研究目标
  - 实现高分辨率文本-图像生成的少步（2∼4步）快速推理
  - 适配定制数据集，保留高效推理能力
## 二、核心方法：Latent Consistency Models (LCMs)
- 1. 基础框架
  - 依赖Stable Diffusion的自编码器（E/D）：z=E(x)，x=D(z)
  - 核心：潜在空间预测增强PF-ODE的t=0解（z₀）
- 2. 关键技术
  - ① 潜在空间一致性蒸馏（LCD）
    - 一致性函数f_θ(z_t, c, t)→z₀，支持ε/v预测参数化
  - ② 一步引导蒸馏
    - 增强PF-ODE融合CFG：ε̃_θ=(1+ω)ε_θ(c)-ωε_θ(∅)
    - 损失函数含ω采样（ω∈[2,14]）
  - ③ SKIPPING-STEP
    - k=20，时间步从1000→几十，加速收敛
    - 损失对齐t_{n+k}与t_n的预测结果
  - ④ Latent Consistency Fine-tuning (LCF)
    - 随机选t_n/t_{n+k}，加相同噪声得z_{t_n}/z_{t_{n+k}}
    - 无需定制数据集的教师模型，30K迭代适配
## 三、预备知识
- 1. 扩散模型
  - 前向SDE：dx_t=f(t)x_t dt+g(t)dw_t
  - 反向PF-ODE：dx_t/dt=f(t)x_t + g²(t)ε_θ/(2σ_t)
  - CFG：ω调节条件/无条件噪声预测权重
- 2. 一致性模型
  - 一致性映射f(x_t, t)→x_ε，自一致性f(x_t,t)=f(x_t',t')
  - EMA目标模型θ⁻=μθ⁻+(1-μ)θ，损失d(f_θ(x_{t+1}),f_θ⁻(x_t^hat))
## 四、实验设计与结果
- 1. 数据集
  - LAION-Aesthetics-6+（12M，512×512）
  - LAION-Aesthetics-6.5+（650K，768×768）
  - Pokemon/Simpsons（定制，数百文本-图像对）
- 2. 模型配置
  - 教师模型：SD-V2.1-Base（512×512，ε预测）/SD-V2.1（768×768，v预测）
  - 训练参数：100K迭代，批量72（512）/16（768），学习率8e-6，EMA=0.999943
- 3. 核心结果
  - 512×512：1步FID 35.36（超Guided-Distill的108.21），CLIP 24.14
  - 768×768：2步FID 16.32（超DPM++的67.14），CLIP 27.92
  - LCF：30K迭代生成Pokemon/Simpsons定制风格图像
## 五、结论与未来方向
- 1. 结论
  - LCMs实现少步（2∼4步）高效推理，性能SOTA
  - LCF低成本适配定制数据集
- 2. 未来
  - 扩展至文本引导图像编辑、修复、超分辨率

---

3. 详细总结

1. 研究背景与核心目标

• 问题痛点：Latent Diffusion Models（LDMs，如Stable Diffusion）虽能生成高分辨率文本-图像，但迭代采样过程计算密集，生成速度慢（需数十步）；现有Consistency Models仅支持像素空间生成，无法适配高分辨率和文本条件任务。
• 核心目标：提出LCMs，在预训练LDM基础上实现2∼4步甚至1步的快速推理，同时保持高生成质量；并设计LCF方法适配定制数据集。

2. 相关工作梳理

模型类型	核心特点	局限
扩散模型	训练稳定、数据似然估计优，通过反向去噪生成样本	迭代采样慢，实时性差
扩散模型加速方法	无训练型（ODE solver如DDIM/DPM，10∼20步）；训练型（蒸馏如Guided-Distill）	Guided-Distill需两阶段蒸馏，成本高（≥45 A100 GPU天），易累积误差
LDMs（如SD）	利用自编码器将图像压缩至潜在空间，降低计算量，支持高分辨率生成	仍需多步迭代，生成速度未根本解决
Consistency Models	学习一致性映射，支持1步生成，无需迭代	仅局限于像素空间，不支持文本条件和高分辨率生成

3. 预备知识核心要点

3.1 扩散模型关键公式

• 前向SDE：描述数据添加噪声的过程，$d{x}_t=f(t)x_{t}dt+g(t)d{w}_t$，其中$w_t$为标准布朗运动，$f(t)=\frac{d\log \alpha (t)}{dt}$，$g^2(t)=\frac{d{\sigma }^2(t)}{dt}-2\frac{d\log \alpha (t)}{dt}{\sigma }^2(t)$。
• 反向PF-ODE：去噪过程的核心，$\frac{d{x}_t}{dt}=f(t)x_t+\frac{g^2(t)}{2{\sigma }_t}{ϵ}_{\theta }(x_t,t)$，${ϵ}_{\theta }$为噪声预测模型，目标是从$x_T$（纯噪声）反向求解$x_0$（真实样本）。
• Classifier-Free Guidance (CFG)：通过$\omega$调节条件与无条件预测的权重，公式为${\widetilde{ϵ}}_{\theta }(z_t,\omega ,c,t)=(1+\omega ){ϵ}_{\theta }(z_t,c,t)-\omega {ϵ}_{\theta }(z_t,\varnothing ,t)$，$\omega$通常取2∼14，提升生成质量与文本对齐度。

3.2 一致性模型核心机制

• 一致性映射：$f(x_t,t)\mapsto x_{ϵ}$（$ϵ$为极小值），需满足自一致性属性：$f(x_t,t)=f(x_{t^{\prime }},t^{\prime })$（任意$t,t^{\prime }\in [ϵ,T]$）。
• EMA目标模型：维护${\theta }^{-}=\mu {\theta }^{-}+(1-\mu )\theta$（$\mu =0.999943$），通过损失$\mathcal{L}(\theta ,{\theta }^{-};\Phi )={\mathbb{E}}_{x,t}[d(f_{\theta }(x_{t_{n+1}},t_{n+1}),f_{{\theta }^{-}}({\hat{x}}_{t_n}^{\varphi },t_n))]$ enforce一致性。

4. LCMs核心方法详解

4.1 潜在空间一致性蒸馏（LCD）

• 核心思想：复用Stable Diffusion的自编码器（$E$：图像→潜在z；$D$：z→图像），在潜在空间$z$中实现一致性蒸馏，而非像素空间（降低计算量）。
• 一致性函数参数化：
  • 若教师模型为$ϵ$-预测（如SD-V2.1-Base）：$f_{\theta }(z,c,t)=c_{skip}(t)z+c_{out}(t)\cdot \frac{z-{\sigma }_t{\widehat{ϵ}}_{\theta }(z,c,t)}{{\alpha }_t}$，其中$c_{skip}(0)=1$，$c_{out}(0)=0$。
  • 若教师模型为$v$-预测（如SD-V2.1）：$f_{\theta }(z,c,t)=c_{skip}(t)z+c_{out}(t)\cdot ({\alpha }_t{z}_t-{\sigma }_t{v}_{\theta }(z_t,c,t))$。

4.2 一步引导蒸馏（融合CFG）

• 增强PF-ODE：将CFG融入PF-ODE，公式为$\frac{d{z}_t}{dt}=f(t)z_t+\frac{g^2(t)}{2{\sigma }_t}{\widetilde{ϵ}}_{\theta }(z_t,\omega ,c,t)$，解决Consistency Models不支持文本条件的问题。
• 损失函数：引入$\omega$的均匀采样（$\omega \in [2,14]$），损失为${\mathcal{L}}_{CD}(\theta ,{\theta }^{-};\Psi )={\mathbb{E}}_{z,c,\omega ,n}[d(f_{\theta }(z_{t_{n+1}},\omega ,c,t_{n+1}),f_{{\theta }^{-}}({\hat{z}}_{t_n}^{\Psi ,\omega },\omega ,c,t_n))]$，其中${\hat{z}}_{t_n}^{\Psi ,\omega }$由增强PF-ODE求解器（如DDIM）估计。

4.3 SKIPPING-STEP技术

• 问题解决：传统SD时间步为1000，相邻步$z_{t_n}$与$z_{t_{n+1}}$差异小，损失小导致收敛慢。
• 实现方式：跳过$k$步（实验中$k=20$），对齐$t_{n+k}$与$t_n$的预测结果，将时间步从1000缩短至几十，大幅加速收敛。
• 修改后损失：${\mathcal{L}}_{CD}(\theta ,{\theta }^{-};\Psi )={\mathbb{E}}_{z,c,\omega ,n}[d(f_{\theta }(z_{t_{n+k}},\omega ,c,t_{n+k}),f_{{\theta }^{-}}({\hat{z}}_{t_n}^{\Psi ,\omega },\omega ,c,t_n))]$。

4.4 Latent Consistency Fine-tuning (LCF)

• 核心作用：将预训练LCM高效适配到定制数据集（如Pokemon、Simpsons），无需在定制数据上训练教师扩散模型。
• 实现步骤：
  1. 编码定制数据至潜在空间：$z=E(x)$，构建数据集$D_z=\{(z,c)|(x,c)\in D_{定制}\}$。
  2. 随机采样$(z,c)$、$n$（$n\in [1,N-k]$）、$\omega$，生成相同噪声$ϵ$，得到$z_{t_n}=\alpha (t_n)z+\sigma (t_n)ϵ$、$z_{t_{n+k}}=\alpha (t_{n+k})z+\sigma (t_{n+k})ϵ$。
  3. 计算损失$\mathcal{L}=d(f_{\theta }(z_{t_{n+k}},\omega ,c,t_{n+k}),f_{{\theta }^{-}}(z_{t_n},\omega ,c,t_n))$，更新模型。
• 训练效率：30K迭代（学习率8e-6）即可生成定制风格图像。

5. 实验结果与分析

5.1 实验配置

配置项	512×512分辨率	768×768分辨率
数据集	LAION-Aesthetics-6+（12M文本-图像对）	LAION-Aesthetics-6.5+（650K文本-图像对）
教师模型	Stable Diffusion-V2.1-Base（ε预测）	Stable Diffusion-V2.1（v预测）
训练迭代	100K	100K
批量大小	72（原Guided-Distill为512）	16
学习率	8e-6	8e-6
EMA速率	0.999943	0.999943
ODE求解器与k值	DDIM，k=20	DDIM，k=20
CFG scale范围	[2,14]	[2,14]

5.2 核心性能结果（ω=8）

模型	分辨率	1步FID（↓）	2步FID（↓）	4步FID（↓）	1步CLIP（↑）	2步CLIP（↑）	4步CLIP（↑）
DDIM	512×512	183.29	81.05	22.38	6.03	14.13	25.89
DPM++	512×512	185.78	72.81	18.43	6.35	15.10	26.64
Guided-Distill	512×512	108.21	33.25	15.12	12.08	22.71	27.25
LCM（本文）	512×512	35.36	13.31	11.10	24.14	27.83	28.69
DDIM	768×768	186.83	77.26	24.28	6.93	16.32	26.48
DPM++	768×768	188.91	67.14	20.08	7.41	17.11	27.26
Guided-Distill	768×768	120.28	30.70	16.70	12.88	24.88	28.45
LCM（本文）	768×768	34.22	16.32	13.53	25.32	27.92	28.60

• 结论：LCM在1∼4步推理下的FID（越低越好）和CLIP（越高越好）分数均显著超越所有基线，尤其1步推理优势最大（512×512 FID仅35.36，远超Guided-Distill的108.21）。

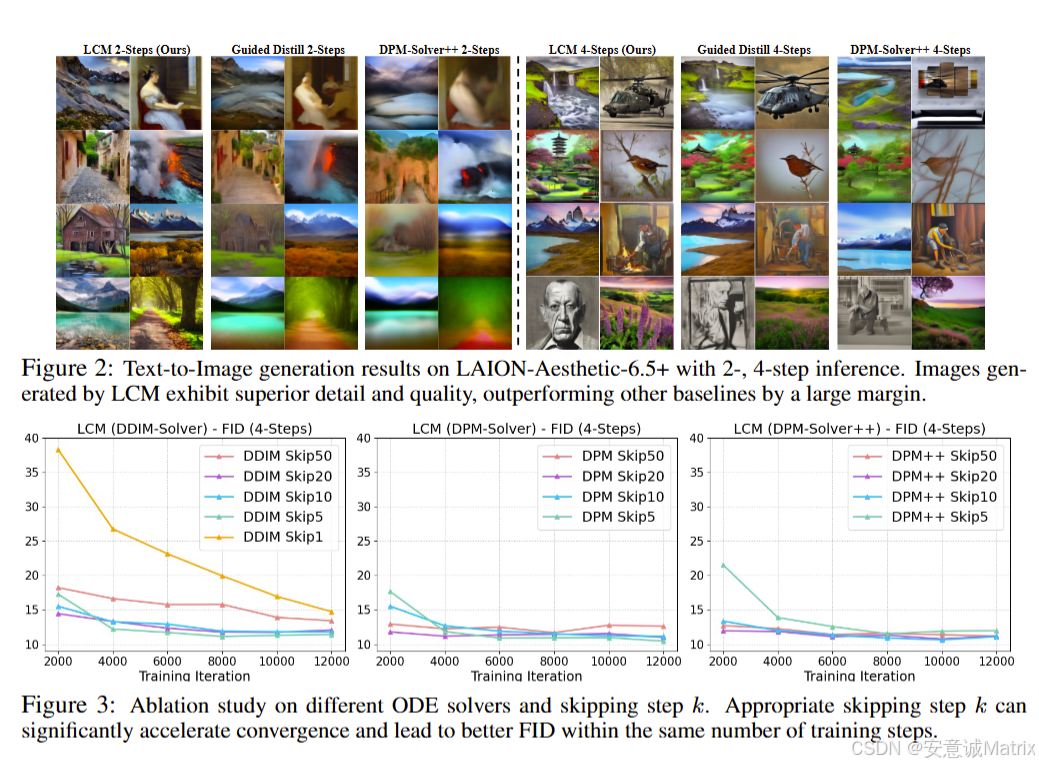
5.3 消融实验关键发现

• ODE求解器对比：DDIM在k=20时收敛最优，DPM/DPM++可支持更大k（如k=50）但复杂度更高；
• k值影响：k=1收敛极慢，k=5∼20收敛加速，k=50（DDIM）因ODE近似误差增大性能下降，故选择k=20；
• CFG scale（ω）影响：ω越大，CLIP分数越高（质量越好），但FID略有上升（多样性略降）；2∼8步推理性能差距小，1步仍有优化空间。

6. 结论与未来方向

• 核心结论：
  1. LCMs通过潜在空间蒸馏、一步引导蒸馏和SKIPPING-STEP，实现2∼4步高分辨率（768×768）生成，训练成本仅32 A100 GPU小时；
  2. LCF可高效适配定制数据集，无需定制教师模型；
  3. LAION-5B-Aesthetics数据集上验证LCMs为少步推理的SOTA模型。
• 未来方向：将LCMs扩展至文本引导图像编辑、图像修复、超分辨率等任务。

---

4. 关键问题与答案

问题1：LCMs通过哪些技术创新实现了“少步（2∼4步）高分辨率生成”与“低训练成本”的平衡？

答案：LCMs通过三项核心技术实现平衡：

1. 潜在空间复用：直接使用Stable Diffusion的自编码器（E/D）将图像压缩至低维潜在空间$z$，相比Consistency Models的像素空间，计算量降低一个数量级，为高分辨率少步生成奠定基础；
2. 一步引导蒸馏：将CFG直接融入增强PF-ODE，避免Guided-Distill的两阶段蒸馏，减少累积误差，同时损失函数中采样$\omega$（2∼14）确保文本对齐，训练仅需100K迭代（32 A100 GPU小时），远低于Guided-Distill的45 A100 GPU天；
3. SKIPPING-STEP技术：通过k=20跳过冗余时间步，将传统SD的1000步时间 schedule缩短至几十步，既加速模型收敛（2000迭代内达到稳定FID），又避免因步长过大导致的生成质量下降。

问题2：在文本-图像生成任务中，LCMs相比传统加速方法（如DDIM、DPM++）的核心优势是什么？从“速度-质量”维度具体说明。

答案：核心优势是在“极快速度（1∼4步）”下保持“SOTA生成质量”，具体对比如下：

1. 速度维度：DDIM、DPM++需10∼20步才能达到可接受质量，而LCMs仅需2∼4步，甚至1步即可生成高分辨率图像（768×768），推理速度提升3∼5倍；且LCMs每步仅需1次前向传播，内存占用比含CFG的DDIM/DPM++更低；
2. 质量维度：以512×512分辨率为例（ω=8）：
   • 1步推理：LCM的FID=35.36，CLIP=24.14，而DDIM的FID=183.29、CLIP=6.03，DPM++的FID=185.78、CLIP=6.35，质量差距悬殊；
   • 2步推理：LCM的FID=13.31，CLIP=27.83，而DDIM的FID=81.05、CLIP=14.13，DPM++的FID=72.81、CLIP=15.10，LCM在质量上实现碾压式超越。
     本质是LCMs直接预测PF-ODE的最终解（z₀），而非逐步去噪，避免了传统方法的累积误差。

问题3：Latent Consistency Fine-tuning (LCF)相比传统扩散模型微调（如LoRA），在适配定制数据集时具有哪些独特优势？

答案：LCF相比传统微调（如LoRA）的优势体现在“效率”和“依赖条件”两方面：

1. 无需定制教师模型：传统扩散模型微调（如LoRA）需依赖预训练LDM（如SD）在定制数据集上的适配版本（或额外训练教师模型），而LCF直接基于预训练LCM进行微调，无需在定制数据上训练任何教师扩散模型，大幅降低数据依赖和前置成本；
2. 训练效率更高：传统LoRA微调需数万至数十万迭代才能稳定，而LCF仅需30K迭代（学习率8e-6）即可在Pokemon/Simpsons等定制数据集上生成符合风格的图像，且保持2∼4步的快速推理能力；
3. 保留少步推理特性：传统微调易因参数更新破坏原模型的少步推理能力，而LCF通过“相同噪声添加+自一致性损失”，在适配定制风格的同时，严格保留LCMs的少步（2∼4步）高效推理特性，避免微调后推理速度退化。