基于驭风25-1-自然语言训练营第一章NLP模型基础完成以下内容。

# 作业一 Word2Vec&TranE的实现

## 案例简介

Word2Vec是词嵌入的经典模型，它通过词之间的上下文信息来建模词的相似度。TransE是知识表示学习领域的经典模型，它借鉴了Word2Vec的思路，用“头实体+关系=尾实体”这一简单的训练目标取得了惊人的效果。本次任务要求在给定的框架中分别基于Text8和Wikidata数据集实现Word2Vec和TransE，并用具体实例体会词向量和实体/关系向量的含义。

---

## A Word2Vec实现

在这个部分，你需要基于给定的代码实现Word2Vec，在Text8语料库上进行训练，并在给定的WordSim353数据集上进行测试

WordSim353是一个词语相似度基准数据集，在WordSim353数据集中，表格的第一、二列是一对单词，第三列中是该单词对的相似度的人工打分(第三列也已经被单独抽出为ground_truth.npy)。我们需要用我们训练得到的词向量对单词相似度进行打分，并与人工打分计算相关性系数，总的来说，越高的相关性系数代表越好的词向量质量。

我们提供了一份基于gensim的Word2Vec实现，请同学们阅读代码并在Text8语料库上进行训练, 关于gensim的Word2Vec模型更多接口和用法，请参考[2]。

由于gensim版本不同，模型中的size参数可能需要替换为vector_size（不报错的话不用管）

运行`word2vec.py` 后，模型会保存在`word2vec_gensim`中，同时代码会加载WordSim353数据集，进行词对相关性评测，得到的预测得分保存在score.npy文件中

之后在Word2Vec文件夹下运行 ``python evaluate.py score.npy``, 程序会自动计算score.npy 和ground_truth.npy 之间的相关系数得分，此即为词向量质量得分。

### 任务

- 运行`word2vec.py`训练Word2Vec模型, 在WordSim353上衡量词向量的质量。

- 探究Word2Vec中各个参数对模型的影响，例如词向量维度、窗口大小、最小出现次数。

- （选做）对Word2Vec模型进行改进，改进的方法可以参考[3]，包括加入词义信息、字向量和词汇知识等方法。请详细叙述采用的改进方法和实验结果分析。

### 快速上手（参考）

在Word2Vec文件夹下运行 ``python word2vec.py``, 即可成功运行, 运行生成两个文件 word2vec_gensim和score.npy。

---

## B TransE实现

这个部分中，你需要根据提供的代码框架实现TransE，在wikidata数据集训练出实体和关系的向量表示，并对向量进行分析。

在TransE中，每个实体和关系都由一个向量表示，分别用$h, r,t$表示头实体、关系和尾实体的表示向量，首先对这些向量进行归一化

则得分函数(score function)为

其中表示向量的范数。得分越小，表示该三元组越合理。

在计算损失函数时，TransE采样一对正例和一对负例，并让正例的得分小于负例，优化下面的损失函数

其中, 别表示正例和负例，是​一个超参数(margin)，用于控制正负例的距离。

### 任务

- 在文件`TransE.py`中，你需要补全`TransE`类中的缺失项，完成TransE模型的训练。需要补全的部分为：

  - `_calc()`：计算给定三元组的得分函数(score function)

  - `loss()`：计算模型的损失函数(loss function)

- 完成TransE的训练，得到实体和关系的向量表示，存储在`entity2vec.txt`和`relation2vec.txt`中。

- 给定头实体Q30，关系P36，最接近的尾实体是哪些？

- 给定头实体Q30，尾实体Q49，最接近的关系是哪些？

- 在 https://www.wikidata.org/wiki/Q30 和 https://www.wikidata.org/wiki/Property:P36 中查找上述实体和关系的真实含义，你的程序给出了合理的结果吗？请分析原因。

- （选做）改变参数`p_norm`和`margin`，重新训练模型，分析模型的变化。

## 快速上手（参考）

在TransE文件夹下运行 ``python TransE.py``, 可以看到程序在第63行和第84行处为填写完整而报错，将这两处根据所学知识填写完整即可运行成功代码（任务第一步），然后进行后续任务。

## 评分标准

请提交代码和实验报告，评分将从代码的正确性、报告的完整性和任务的完成情况等方面综合考量。

## 参考资料

[1] https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient

[2] https://radimrehurek.com/gensim/models/word2vec.html

[3] A unified model for word sense representation and disambiguation. in Proceedings of EMNLP, 2014.

1.Word2Vec实现

1.1 Word2Vec原理

Word2Vec 是一种非常著名的词向量（Word Embedding）技术，由 Google 在 2013 年提出，用于将自然语言中的词语转化为计算机可以理解的数值向量。它的基本理念是一个词的意义（meaning）是由它周围的词决定的。因此，我们会使用一个固定大小的窗口沿着句子滑动，在每一个窗口中，选择一个词作为中心词（一般为中间的那个词），其他词作为上下文，两两组成训练样本。如下图所示（窗口为5）：

Word2Vec的核心架构：

1.1.1连续词袋模型（CBOW: Continuous Bag of Words）

CBOW的核心思想是根据上下文预测中心词，简单来说，就是模型取目标词前后各N个单词，再根据这些单词在词嵌入矩阵中对应的向量进行相应的计算，最后得出的向量来预测目标词。CBOW适合较小的词汇表和较短的上下文窗口，具有训练效率高、对常见词效果好，能平滑噪音等优点。但不擅长处理罕见词的语义。

1.1.2跳跃式模型（Skip-Gram）

Skip-Gram的核心思想是根据中心词预测它周围的上下文，模型取中心词在词嵌入矩阵中的向量进行计算，分多次预测所有上下文，所以它的缺点明显，训练速度慢，但是它的优点很多，能够更好的学习罕见词的语义，捕捉更多的词义细节。Skip-Gram通常相比CBOW更准确，特别是在较大词汇表和更长上下文窗口的表现。

1.2 Word2Vec代码

Word2Vec实验已给出相应代码，Word2Vec训练代码如下：

import gensim  # 导入 gensim 库，用于训练 Word2Vec 模型
import logging  # 导入 logging，用于记录训练过程中的日志信息
import multiprocessing  # 导入多进程库，用于并行加速训练
from gensim.models import word2vec  # 从 gensim 中导入 word2vec 相关工具
import numpy as np  # 导入 numpy，用于数值计算与保存结果
from time import time  # 导入 time，用于计时

logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s',
                    level=logging.INFO)  # 配置日志输出格式与级别

if __name__ == '__main__':  # 仅当作为脚本运行时执行以下代码

    data_path = 'text8'  # 数据文件路径（text8语料）
    t = time()  # 记录开始时间

    # loading dataset
    sents = word2vec.Text8Corpus('text8')  # 加载 text8 语料，按句子迭代

    # training word2vec
    model = gensim.models.Word2Vec(sents,  # 训练 Word2Vec 模型
                                   vector_size=200,  # 词向量维度
                                   window=10,  # 上下文窗口大小
                                   min_count=30,  # 词频阈值（低于该频次的词会被忽略）
                                   sg=0,  # 训练算法：1 为 Skip-gram，0 为 CBOW
                                   workers=multiprocessing.cpu_count())  # 使用CPU核心数进行并行训练

    # saving to file
    model.save("word2vec_gensim")  # 保存 gensim 模型文件
    model.wv.save_word2vec_format("word2vec_org",  # 导出词向量到文本格式
                                  "vocabulary",  # 导出词表（与向量对应的词）
                                  binary=False)  # 以文本格式保存，而非二进制

    print ("Total time: %d s" % (time() - t))  # 打印训练总耗时（秒）
    
    # testing on wordsim353
    sims = []  # 存放模型计算的相似度分数
    ground_truth = []  # 存放数据集中的人工标注相似度
    with open('wordsim353/combined.csv') as f:  # 打开 wordsim353 测试集
        for line in f.readlines()[1:]:  # 跳过首行表头，逐行读取
            l = line.strip().split(',')  # 逗号分隔得到 [词1, 词2, 人工分]
            if l[0] in model.wv.key_to_index and l[1] in model.wv.key_to_index:  # 过滤掉不在词表内的词
                sims.append(model.wv.similarity(l[0], l[1]))  # 模型打分：计算两个词的余弦相似度
                ground_truth.append(float(l[2]))  # 记录人工标注的分数（转为浮点数）
    
    np.save('score.npy', np.array(sims))  # 将模型分数保存为 numpy 数组文件
    np.save('ground_truth.npy', np.array(ground_truth))  # 将人工分数保存为 numpy 数组文件

代码主要使用gensim库对Word2Vec进行训练，更多方法可以查看【2】了解学习。运行完程序后得到'score.npy'和'ground_truth.npy'用于后续的评估与分析。

评估代码如下：

import sys  # 导入 sys 用于读取命令行参数
# 用于打印JSON编码的评分结果
import json  # 导入 json 用于输出评测结果为 JSON 字符串
import numpy as np  # 导入 numpy 用于加载与处理 .npy 文件
from scipy.stats import spearmanr  # 从 scipy 导入 spearmanr 计算斯皮尔曼相关系数


def eval(submit_file):  # 定义评估函数，参数为命令行参数列表（通常是 sys.argv）
    # 如果未传入参数，默认使用当前目录下的 score.npy
    try:  # 捕获可能的文件与运行时异常
        sims_path = submit_file[1] if len(submit_file) > 1 else 'score.npy'  # 若提供参数则用之，否则默认 score.npy
        sims = np.load(sims_path)  # 读取模型生成的相似度得分数组
        score = np.load('ground_truth.npy')  # 读取人工标注的标准分数组
        # 计算Spearman相关系数
        spcor = spearmanr(score, sims)[0]  # 取 spearmanr 返回的相关系数（第一个元素）
        # 以下返回值主要用于aistudio的比赛，但是本次实验不设置比赛，大家只用看score的值
        return {
            "score": spcor,              # 替换为最终评测分数（核心输出）
            "errorMsg": "success",      # 错误提示信息（成功时为 success）
            "code": 0,                  # code 为 0 表示成功，非 0 表示失败
            "data": [                   # 可选的数据字段（保持原结构）
                {
                    "score": spcor      # 冗余地再次放置分数
                }
            ]
        }
    except FileNotFoundError as e:  # 当文件路径不正确或文件不存在时的异常处理
        return {
            "score": 0.0,                # 失败时分数置为 0.0（占位）
            "errorMsg": f"文件未找到: {e}",  # 返回详细的文件未找到信息
            "code": 1,                   # 非 0 表示失败
            "data": []                   # 失败时 data 为空列表
        }
    except Exception as e:  # 其他所有类型异常的兜底处理
        return {
            "score": 0.0,                # 失败时分数占位
            "errorMsg": f"运行出错: {e}",   # 返回异常信息
            "code": 1,                   # 非 0 表示失败
            "data": []                   # 失败时 data 为空
        }


if __name__ == '__main__':  # 脚本入口：仅当直接运行该文件时执行
    # 打印格式必须为JSON编码的字符串
    print(json.dumps(eval(sys.argv)))  # 调用评估函数并以 JSON 字符串形式打印输出

使用spearman相关系数，评估 Word2Vec 模型生成的单词相似度分数与真实分数之间的相关性。（Spearman 相关系数（Spearman's Rank Correlation Coefficient）是一种非参数统计方法，用来衡量两个变量之间的单调关系（monotonic relationship）。它不关心变量之间是不是线性关系，而是关心：一个变量增大时，另一个变量是否也倾向于增大（或减小）。

）

1.3 参数对模型的影响

本次实验我们需要从词向量维度、窗口大小、最小出现次数三个维度探讨其对score分数和Time(s)训练时间的影响。

A.固定窗口大小与最小出现次数，调整词向量维度

1.词向量维度=200、窗口大小=10、最小出现次数=10。

{"score": 0.6924131907316371}

2.词向量维度=50、窗口大小=10、最小出现次数=10。

{"score": 0.6682678312695682}

3.词向量维度=100、窗口大小=10、最小出现次数=10。

{"score": 0.683491081977539}

4.词向量维度=150、窗口大小=10、最小出现次数=10。

{"score": 0.6930524869189425}

5.词向量维度=250、窗口大小=10、最小出现次数=10。

{"score": 0.6888651706759551}

6.词向量维度=300、窗口大小=10、最小出现次数=10。

{"score": 0.6899484817581628}

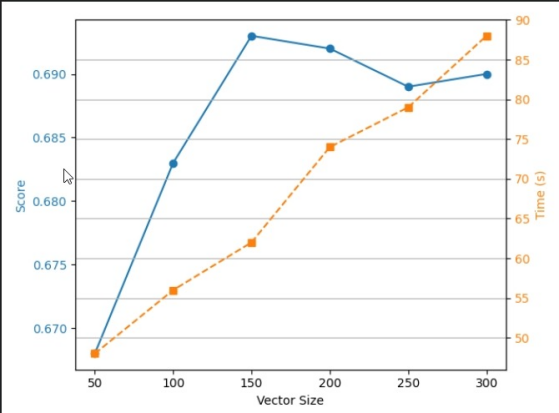
可以看出，随着Vector Size的增大，训练时间不断增加，而Score先增加后降低，再Vector Size为150时，取得最大值0.693.

B.固词向量维度与最小出现次数，调整窗口大小

1.窗口大小=10、词向量维度=200、最小出现次数=10。

{"score": 0.6924131907316371}

2.窗口大小=5、词向量维度=200、最小出现次数=10。

{"score": 0.6452402153594002}

3.窗口大小=15、词向量维度=200、最小出现次数=10。

{"score": 0.7101534549741877}

4.窗口大小=20、词向量维度=200、最小出现次数=10。

{"score": 0.7250984585342083}

5.窗口大小=25、词向量维度=200、最小出现次数=10。

{"score": 0.7163290003957505}

6.窗口大小=30、词向量维度=200、最小出现次数=10。

{"score": 0.723594415465177}

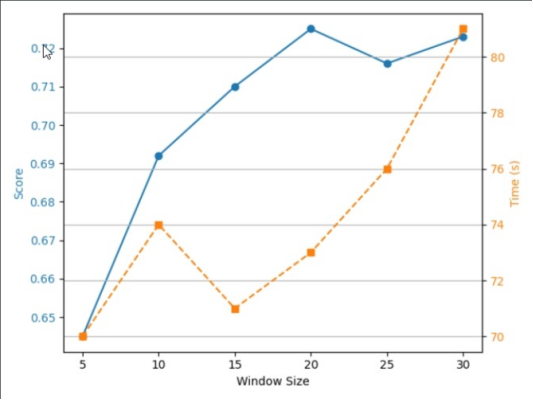
随着Window Size增加，训练时间先增加，后下降，然后继续上升，总体在70-81之间波动，Score先增加后在Window Size为25时下降后上升，在Window Size为20取得最大值0.725.

C.固词向量维度与窗口大小，调整最小出现次数

1.最小出现次数=10、窗口大小=10、词向量维度=200。

{"score": 0.6924131907316371}

2.最小出现次数=5、窗口大小=10、词向量维度=200。

{"score": 0.6787672917295096}

3.最小出现次数=15、窗口大小=10、词向量维度=200。

{"score": 0.6820090939831387}

4.最小出现次数=20、窗口大小=10、词向量维度=200。

{"score": 0.6892887795884203}

5.最小出现次数=25、窗口大小=10、词向量维度=200。

{"score": 0.7080805294688178}

6.最小出现次数=30、窗口大小=10、词向量维度=200。

{"score": 0.6981777498507565}

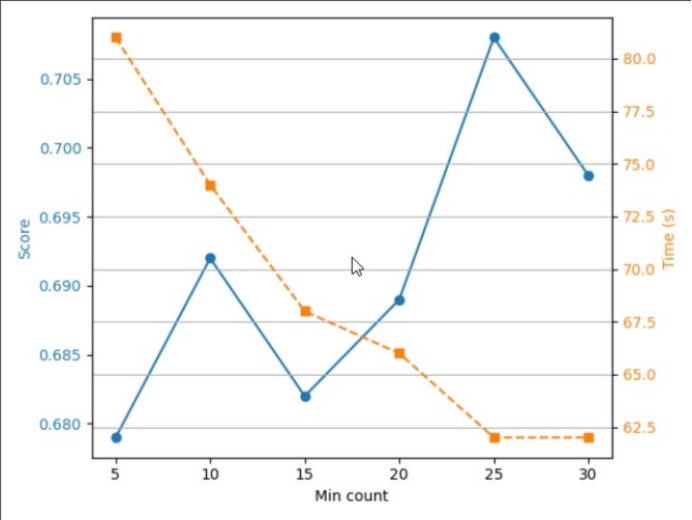
随着Min count的增加，训练时间不断降低，而Score则在0.692-0.708不断波动，在Min count为25时取得最大值0.708.

1.4 模型改进

1.4.1 使用Skip-gram进行训练

为了将CBOW替换为Skip-gram，我们需要将training word2vec中'sg=0'改为'sg=1'，其它参数保持不变。

词向量维度=200、窗口大小=10、最小出现次数=10。

Total Time(s):272

{"score": 0.7218032575325762}

使用Skip-gram进行训练，获得了更好的结果，score分数相比之前score分数多出0.03左右，但消耗时间多出198s。

1.4.2  WordNet 的同义词关系增强词向量

词向量维度=200、窗口大小=10、最小出现次数=10。

代码如下：

import gensim  # 导入 gensim 库，用于训练 Word2Vec 模型
import logging  # 导入 logging，用于记录训练过程中的日志信息
import multiprocessing  # 导入多进程库，用于并行加速训练
from gensim.models import word2vec  # 从 gensim 中导入 word2vec 相关工具
import numpy as np  # 导入 numpy，用于数值计算与保存结果
from time import time  # 导入 time，用于计时
import nltk  # 导入 NLTK 库，用于 WordNet 功能
from nltk.corpus import wordnet  # 从 NLTK 导入 WordNet 语料库
import zipfile  # 导入 zipfile 用于处理压缩文件错误

# 下载 WordNet 数据（如果尚未下载）
try:
    nltk.data.find('corpora/wordnet')
    print("WordNet 数据已存在")
except (LookupError, zipfile.BadZipFile, Exception) as e:
    print(f"WordNet 数据问题: {e}")
    print("正在重新下载 WordNet 数据...")
    try:
        nltk.download('wordnet', quiet=False)
        print("WordNet 数据下载完成")
    except Exception as download_error:
        print(f"下载失败: {download_error}")
        print("请手动运行: nltk.download('wordnet')")
        sys.exit(1)

logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s',
                    level=logging.INFO)  # 配置日志输出格式与级别


def get_synonyms_antonyms(word):
    """获取单词的同义词和反义词"""
    synonyms = []  # 存储同义词列表
    antonyms = []  # 存储反义词列表
    
    for syn in wordnet.synsets(word):  # 遍历该词的所有词义集合
        for lemma in syn.lemmas():  # 遍历每个词义的所有词形
            synonyms.append(lemma.name().replace('_', ' '))  # 添加同义词（替换下划线为空格）
            if lemma.antonyms():  # 如果存在反义词
                antonyms.append(lemma.antonyms()[0].name().replace('_', ' '))  # 添加反义词
    
    # 去重并返回
    return list(set(synonyms)), list(set(antonyms))


def enhance_vector_with_wordnet(model, alpha=0.5):
    """用 WordNet 同义词增强词向量"""
    print("开始使用 WordNet 增强词向量...")
    enhanced_vectors = {}  # 存储增强后的词向量
    total_words = len(model.wv.key_to_index)  # 总词数
    processed = 0  # 已处理词数
    
    for word in model.wv.key_to_index:  # 遍历模型中的所有词
        vector = model.wv[word].copy()  # 复制原始词向量
        synonyms, _ = get_synonyms_antonyms(word)  # 获取同义词和反义词
        synonym_vectors = []  # 存储同义词的向量
        
        for syn in synonyms:  # 遍历同义词
            if syn in model.wv.key_to_index:  # 如果同义词在模型中存在
                synonym_vectors.append(model.wv[syn])  # 添加同义词向量
        
        if synonym_vectors:  # 如果找到同义词向量
            avg_syn_vector = np.mean(synonym_vectors, axis=0)  # 计算同义词向量的平均值
            # 加权融合：原始向量 + 同义词平均向量
            vector = alpha * vector + (1 - alpha) * avg_syn_vector
        
        enhanced_vectors[word] = vector  # 存储增强后的向量
        processed += 1
        
        # 显示进度
        if processed % 1000 == 0:
            print(f"已处理 {processed}/{total_words} 个词...")
    
    print(f"WordNet 增强完成！共处理 {processed} 个词")
    return enhanced_vectors


def calculate_similarity_with_enhanced_vectors(enhanced_vectors, word1, word2):
    """使用增强后的向量计算两个词的相似度"""
    if word1 not in enhanced_vectors or word2 not in enhanced_vectors:
        return None  # 如果任一词不在增强向量中，返回 None
    
    vec1 = enhanced_vectors[word1]  # 获取词1的增强向量
    vec2 = enhanced_vectors[word2]  # 获取词2的增强向量
    
    # 计算余弦相似度
    dot_product = np.dot(vec1, vec2)  # 点积
    norm1 = np.linalg.norm(vec1)  # 向量1的模长
    norm2 = np.linalg.norm(vec2)  # 向量2的模长
    
    if norm1 == 0 or norm2 == 0:  # 避免除零错误
        return 0.0
    
    similarity = dot_product / (norm1 * norm2)  # 余弦相似度
    return similarity


if __name__ == '__main__':  # 仅当作为脚本运行时执行以下代码

    data_path = 'text8'  # 数据文件路径（text8语料）
    t = time()  # 记录开始时间

    # loading dataset
    sents = word2vec.Text8Corpus('text8')  # 加载 text8 语料，按句子迭代

    # training word2vec
    print("开始训练 Word2Vec 模型...")
    model = gensim.models.Word2Vec(sents,  # 训练 Word2Vec 模型
                                   vector_size=200,  # 词向量维度
                                   window=10,  # 上下文窗口大小
                                   min_count=30,  # 词频阈值（低于该频次的词会被忽略）
                                   sg=1,  # 训练算法：1 为 Skip-gram，0 为 CBOW
                                   workers=multiprocessing.cpu_count())  # 使用CPU核心数进行并行训练

    # saving to file
    model.save("word2vec_gensim")  # 保存 gensim 模型文件
    model.wv.save_word2vec_format("word2vec_org",  # 导出词向量到文本格式
                                  "vocabulary",  # 导出词表（与向量对应的词）
                                  binary=False)  # 以文本格式保存，而非二进制

    print("Word2Vec 训练完成！")
    print("Total time: %d s" % (time() - t))  # 打印训练总耗时（秒）
    
    # 使用 WordNet 增强词向量
    enhanced_vectors = enhance_vector_with_wordnet(model, alpha=0.7)  # 增强词向量，权重为0.7
    
    # testing on wordsim353 with enhanced vectors
    print("开始使用增强向量在 wordsim353 上测试...")
    sims = []  # 存放模型计算的相似度分数
    ground_truth = []  # 存放数据集中的人工标注相似度
    valid_pairs = 0  # 有效词对数量
    
    with open('wordsim353/combined.csv') as f:  # 打开 wordsim353 测试集
        for line in f.readlines()[1:]:  # 跳过首行表头，逐行读取
            l = line.strip().split(',')  # 逗号分隔得到 [词1, 词2, 人工分]
            if l[0] in enhanced_vectors and l[1] in enhanced_vectors:  # 过滤掉不在增强向量中的词
                similarity = calculate_similarity_with_enhanced_vectors(enhanced_vectors, l[0], l[1])  # 使用增强向量计算相似度
                if similarity is not None:  # 如果成功计算相似度
                    sims.append(similarity)  # 添加模型计算的相似度
                    ground_truth.append(float(l[2]))  # 记录人工标注的分数（转为浮点数）
                    valid_pairs += 1
    
    print(f"有效词对数量: {valid_pairs}")
    
    # 保存增强后的结果
    np.save('score_enhanced.npy', np.array(sims))  # 将增强后的模型分数保存为 numpy 数组文件
    np.save('ground_truth_enhanced.npy', np.array(ground_truth))  # 将对应的人工分数保存为 numpy 数组文件
    
    # 同时保存原始格式的结果（用于兼容性）
    np.save('score.npy', np.array(sims))  # 保存为 score.npy（与原始评估脚本兼容）
    np.save('ground_truth.npy', np.array(ground_truth))  # 保存为 ground_truth.npy（与原始评估脚本兼容）
    
    print("增强向量测试完成！结果已保存到 score.npy 和 ground_truth.npy")
    print("可以使用 evaluation.py 脚本评估增强后的效果")

使用模型生成的score.npy和ground_truth.npy文件去做评估。得到以下结果：

Total Time(s):266s

{"score": 0.7153374160383908}

相比原模型，score分数提高了0.02左右，但训练时间消耗多192s。

2.TransE实现

2.1 TransE原理

TransE是一种经典的知识图谱嵌入（Knowledge Graph Embedding）模型，由Bordes等人于2013年提出。它的核心思想是将知识图谱中的实体（Entity）和关系（Relation）表示为低维连续向量空间中的向量，并通过向量间的“翻译”操作来建模三元组（头实体，关系，尾实体）。它的原理可以用一个简单的几何概念来理解：向量平移。即一个三元组 (h, r, t)（即头实体 h，关系 r，尾实体 t），在向量空间中，头实体向量 h 经过关系向量 r 的“翻译”后，应该接近尾实体向量 t。

2.2 TransE代码

实验给出了TransE的基础代码，但需要补全_calc、loss处的代码。代码如下：

import torch  # 导入PyTorch深度学习框架
import torch.nn as nn  # 导入神经网络模块
import torch.nn.functional as F  # 导入函数式接口，包含激活函数等
import torch.optim as optim  # 导入优化器模块
from torch.autograd import Variable  # 导入自动求导变量（已弃用，但保留兼容性）
from load_data import PyTorchTrainDataLoader  # 导入自定义的数据加载器
import ctypes  # 导入C类型库，用于底层操作
import os  # 导入操作系统接口
import time  # 导入时间处理模块
import numpy as np  # 导入NumPy数值计算库

class Config(object):
    """配置类，存储TransE模型的超参数"""

    def __init__(self):
        self.p_norm = 1  # L1范数，用于计算距离
        self.hidden_size = 50  # 嵌入向量维度
        self.nbatches = 100  # 批处理数量
        self.entity = 0  # 实体数量（运行时设置）
        self.relation = 0  # 关系数量（运行时设置）
        self.trainTimes = 100  # 训练轮数
        self.margin = 1  # 损失函数中的边界值
        self.learningRate = 0.01  # 学习率
        self.use_gpu = False  # 是否使用GPU训练

def to_var(x, use_gpu):
    """将numpy数组转换为PyTorch变量，支持GPU"""
	if use_gpu:  # 如果使用GPU
	    return Variable(torch.from_numpy(x).cuda())  # 将数据移到GPU上
	else:  # 如果使用CPU
	    return Variable(torch.from_numpy(x))  # 在CPU上处理数据

class TransE(nn.Module):
    """TransE知识图谱嵌入模型"""

    def __init__(self, ent_tot, rel_tot, dim = 100, p_norm = 1, norm_flag = True, margin = None):
        '''
        初始化TransE模型
        参数:
        ent_tot: 实体总数
        rel_tot: 关系总数
        dim: 嵌入向量维度
        p_norm: 1 for l1-norm, 2 for l2-norm
        norm_flag: 是否使用归一化
        margin: 损失函数中的边界值
        '''
        super(TransE, self).__init__()  # 调用父类构造函数

        self.dim = dim  # 嵌入向量维度
        self.margin = margin  # 边界值
        self.norm_flag = norm_flag  # 归一化标志
        self.p_norm = p_norm  # 范数类型
        self.ent_tot = ent_tot  # 实体总数
        self.rel_tot = rel_tot  # 关系总数
        
        # 创建实体嵌入层，将实体ID映射为向量
        self.ent_embeddings = nn.Embedding(self.ent_tot, self.dim)
        # 创建关系嵌入层，将关系ID映射为向量
        self.rel_embeddings = nn.Embedding(self.rel_tot, self.dim)

        # 使用Xavier均匀分布初始化实体嵌入权重
        nn.init.xavier_uniform_(self.ent_embeddings.weight.data)
        # 使用Xavier均匀分布初始化关系嵌入权重
        nn.init.xavier_uniform_(self.rel_embeddings.weight.data)
            
        if margin != None:  # 如果指定了边界值
            self.margin = nn.Parameter(torch.Tensor([margin]))  # 创建可学习参数
            self.margin.requires_grad = False  # 设置边界值不需要梯度更新
            self.margin_flag = True  # 设置边界标志为True
        else:  # 如果没有指定边界值
            self.margin_flag = False  # 设置边界标志为False


    def _calc(self, h, t, r):
        """
        计算TransE的得分函数
        核心思想：h + r ≈ t，即头实体向量 + 关系向量 ≈ 尾实体向量
        """
        if self.norm_flag:  # 如果启用归一化
            # 对头实体向量进行L2归一化
            h = F.normalize(h, p=self.p_norm, dim=1)
            # 对尾实体向量进行L2归一化
            t = F.normalize(t, p=self.p_norm, dim=1)
            # 对关系向量进行L2归一化
            r = F.normalize(r, p=self.p_norm, dim=1)
        # 计算得分：||h + r - t||_p，得分越小表示三元组越可能为真
        score = torch.norm(h + r - t, self.p_norm, dim=1)
        return score

    def forward(self, data):
        """前向传播函数"""
        batch_h = data['batch_h']  # 获取批次中的头实体ID
        batch_t = data['batch_t']  # 获取批次中的尾实体ID
        batch_r = data['batch_r']  # 获取批次中的关系ID
        
        # 通过嵌入层获取头实体向量
        h = self.ent_embeddings(batch_h)
        # 通过嵌入层获取尾实体向量
        t = self.ent_embeddings(batch_t)
        # 通过嵌入层获取关系向量
        r = self.rel_embeddings(batch_r)
        
        # 计算得分
        score = self._calc(h, t, r)
        return score

    def predict(self, data):
        """预测函数，返回numpy格式的得分"""
        score = self.forward(data)  # 计算得分
        return score.cpu().data.numpy()  # 转换为numpy数组并返回
    
    def loss(self, pos_score, neg_score):
        """
        计算损失函数
        使用margin ranking loss：max(0, margin + pos_score - neg_score)
        """
        # 计算正例得分与负例得分的差值，加上边界值，然后取ReLU
        return torch.nn.ReLU()(self.margin + (pos_score - neg_score).mean())
        


def main():
    """主函数，执行TransE模型的训练"""
    config = Config()  # 创建配置对象
    
    # 创建数据加载器，从./data/目录加载训练数据
    train_dataloader = PyTorchTrainDataLoader(
                            in_path = "./data/",  # 数据路径
                            nbatches = config.nbatches,  # 批次数
                            threads = 8)  # 线程数
    
    # 创建TransE模型实例
    transe = TransE(
            ent_tot = train_dataloader.get_ent_tot(),  # 实体总数
            rel_tot = train_dataloader.get_rel_tot(),  # 关系总数
            dim = config.hidden_size,  # 嵌入维度
            p_norm = config.p_norm,  # 范数类型
            norm_flag = True,  # 启用归一化
            margin=config.margin)  # 边界值
    
    # 创建SGD优化器
    optimizier = optim.SGD(transe.parameters(), lr=config.learningRate)

    if config.use_gpu:  # 如果使用GPU
        transe.cuda()  # 将模型移到GPU上
    
    # 开始训练循环
    for times in range(config.trainTimes):  # 训练指定轮数
        ep_loss = 0.  # 初始化每轮损失
        for data in train_dataloader:  # 遍历每个批次
            optimizier.zero_grad()  # 清零梯度
            
            # 前向传播，计算得分
            score = transe({
                    'batch_h': to_var(data['batch_h'], config.use_gpu).long(),  # 头实体
                    'batch_t': to_var(data['batch_t'], config.use_gpu).long(),  # 尾实体
                    'batch_r': to_var(data['batch_r'], config.use_gpu).long()})  # 关系
            
            pos_score, neg_score = score[0], score[1]  # 分离正例和负例得分
            loss = transe.loss(pos_score, neg_score)  # 计算损失
            loss.backward()  # 反向传播
            optimizier.step()  # 更新参数
            ep_loss += loss.item()  # 累加损失
        print("Epoch %d | loss: %f" % (times+1, ep_loss))  # 打印每轮损失
    
    print("Finish Training")  # 训练完成提示
    
    # 保存实体嵌入向量到文件
    f = open("entity2vec.txt", "w")  # 打开实体向量文件
    enb = transe.ent_embeddings.weight.data.cpu().numpy()  # 获取实体嵌入权重
    for i in enb:  # 遍历每个实体向量
        for j in i:  # 遍历向量中的每个元素
            f.write("%f\t" % (j))  # 写入数值
        f.write("\n")  # 换行
    f.close()  # 关闭文件

    # 保存关系嵌入向量到文件
    f = open("relation2vec.txt", "w")  # 打开关系向量文件
    enb = transe.rel_embeddings.weight.data.cpu().numpy()  # 获取关系嵌入权重
    for i in enb:  # 遍历每个关系向量
        for j in i:  # 遍历向量中的每个元素
            f.write("%f\t" % (j))  # 写入数值
        f.write("\n")  # 换行
    f.close()  # 关闭文件

            
if __name__ == "__main__":
    main()  # 运行主函数

_calc中需要对h、r、t经行归一化，可以参考学习：torch.nn.functional.normalize — PyTorch 2.8 documentation

loss中根据margin ranking loss：max(0, margin + pos_score - neg_score)给出对应的代码就行了。

2.3 结果分析

其它参数保持不变，将训练轮次trainTimes调整到100.

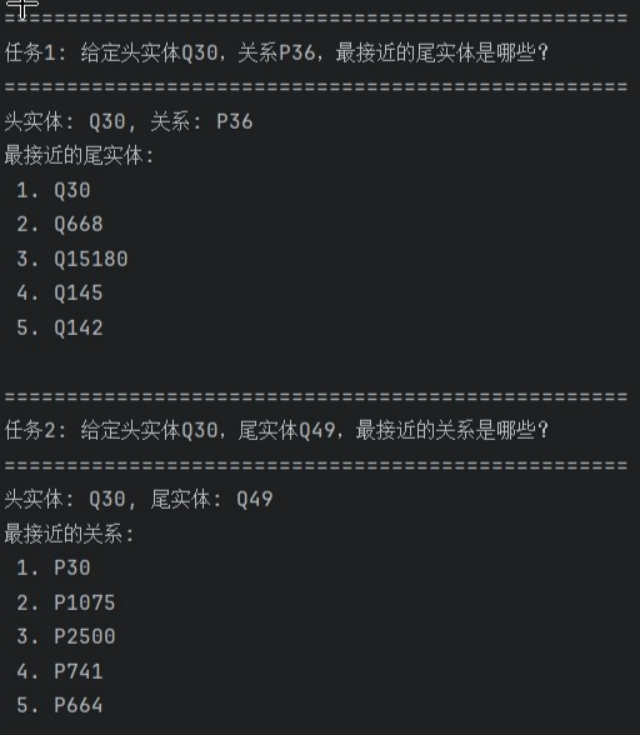
通过在https://www.wikidata.org/wiki/Q30与​​​​​​​https://www.wikidata.org/wiki/Property:P36上查询可以得出实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）

1. Q30(United States)
2. Q668(India)
3. Q15180(Soviet Union)
4. Q145(United Kingdom)
5. Q142(France)

按照正常推理，最接近的关系应该是华盛顿，但给出的关系都不太相符，推测原因可能是训练轮次不够导致损失函数任然偏大(只训练了70轮，损失函数18.68)。

实体Q30（United States），实体Q49(North America),最接近关系（Top5）

1. P30(continent)
2. P1075（rector）
3. P2500(league level below)
4. P741(playing hand)
5. P664(organizer)

两实体关系推测大概与大洲相关，美国位于北美洲，第一个答案相当接近了，但接下来4个答案就相差较远了。

2.4 模型改进

2.4.1更改p_norm

p_norm主要决定score函数中的范数类型，p_norm=1为L1（曼哈顿距离）、p_norm=2为L2（欧几里得距离）,下图是p_norm=1时，模型收敛情况。

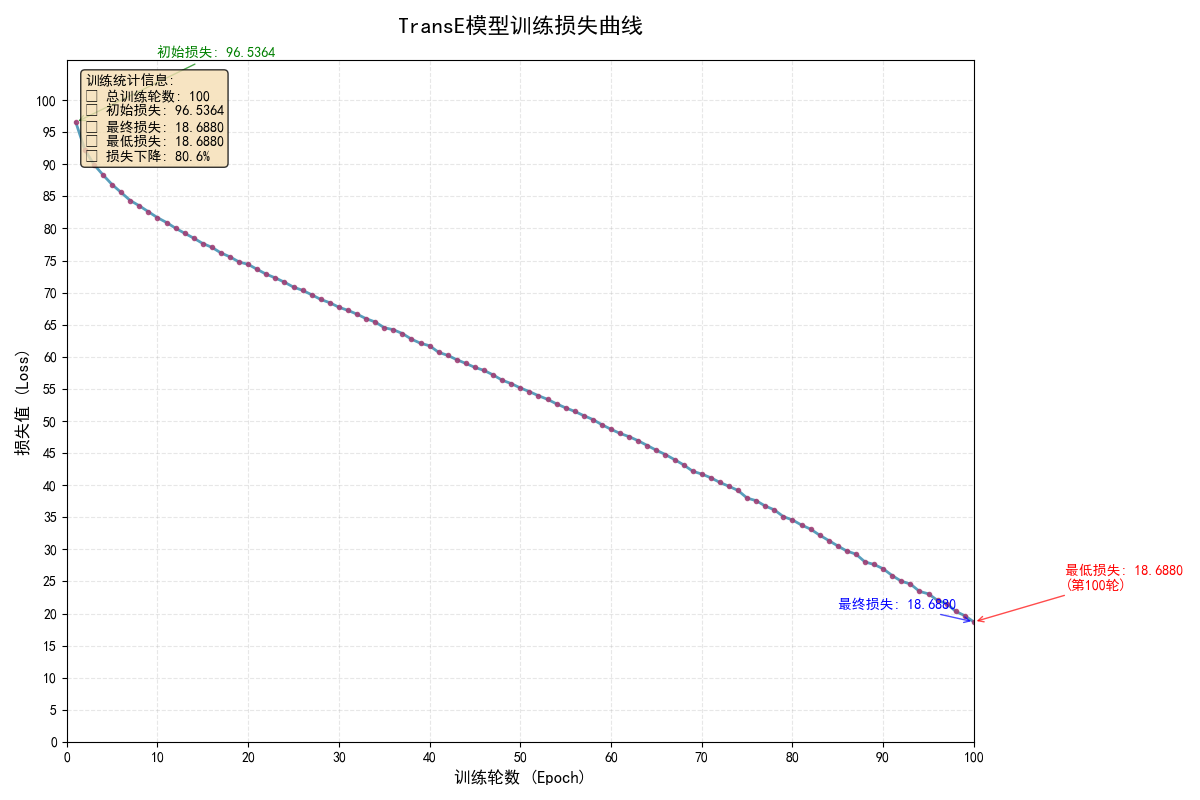
实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）

1. Q30(United States)
2. Q668(India)
3. Q15180(Soviet Union)
4. Q145(United Kingdom)
5. Q142(France)

实体Q30（United States），实体Q49(North America),最接近关系（Top5）

1. P30(continent)
2. P1075（rector）
3. P2500(league level below)
4. P741(playing hand)
5. P664(organizer)

当p_norm=2时，模型收敛情况与结果

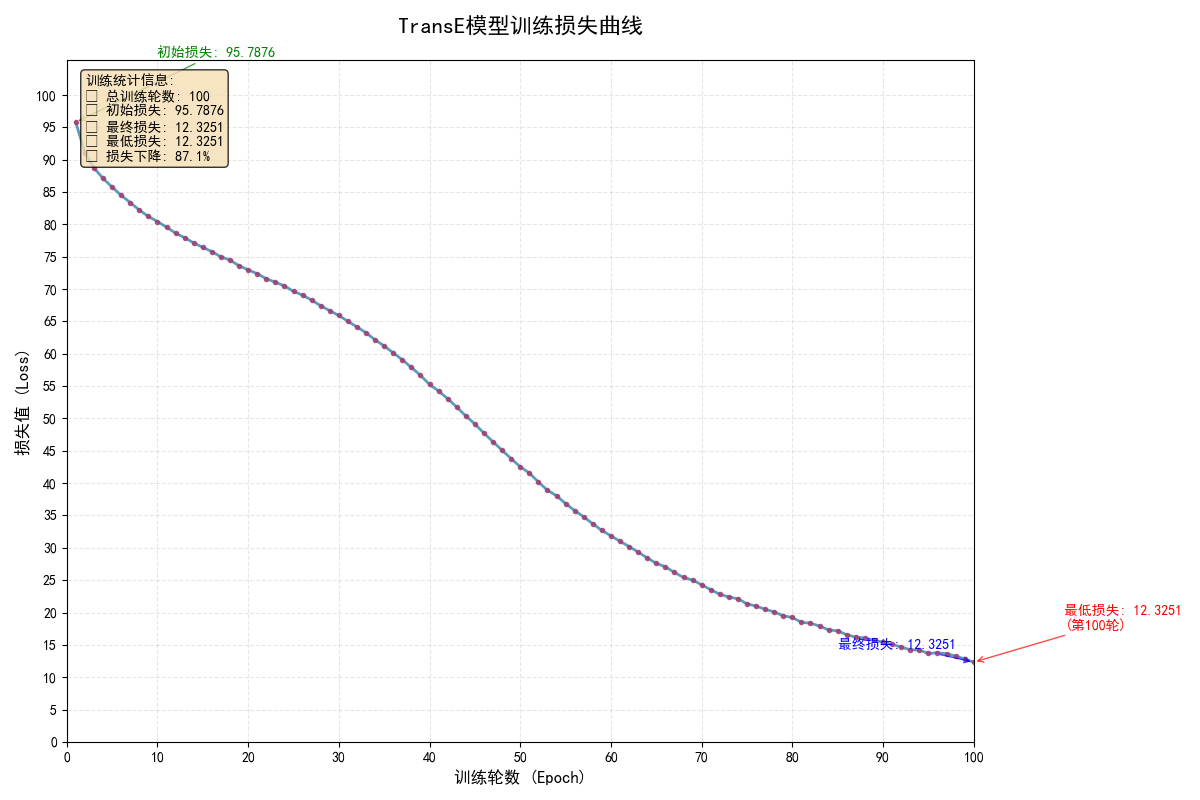
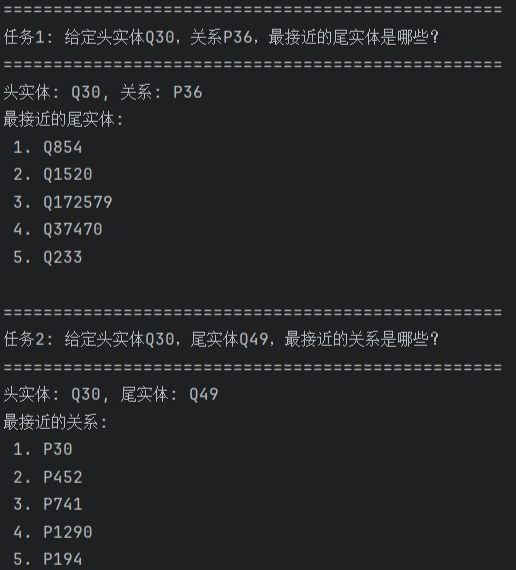
实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）

1. Q854(Sri Lanka)
2. Q1520(Astana)
3. Q172579(Kingdom of Italy)
4. Q37470(United Nations Security Council)
5. Q233(Malta)

实体Q30（United States），实体Q49(North America),最接近关系（Top5）

1. P30(continent)
2. P452（industry）
3. P741(playing hand)
4. P1290(godparent)
5. P194(legislative body)

对比p_norm=1和p_norm=2的两种情况，当p_norm=2时模型收敛更快，且最终loss相比p_norm=1时减少了7.36，但在描述实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）时，给出的答案更差，在描述实体Q30（United States），实体Q49(North America),最接近关系（Top5）时答案都在第一位给对了相应关系。

2.4.2 更改margin 

Margin是TransE损失函数中的一个关键超参数，用于控制正例和负例之间的"安全距离"。下图为分别是margin=1和margain=0.5时的losses收敛情况。

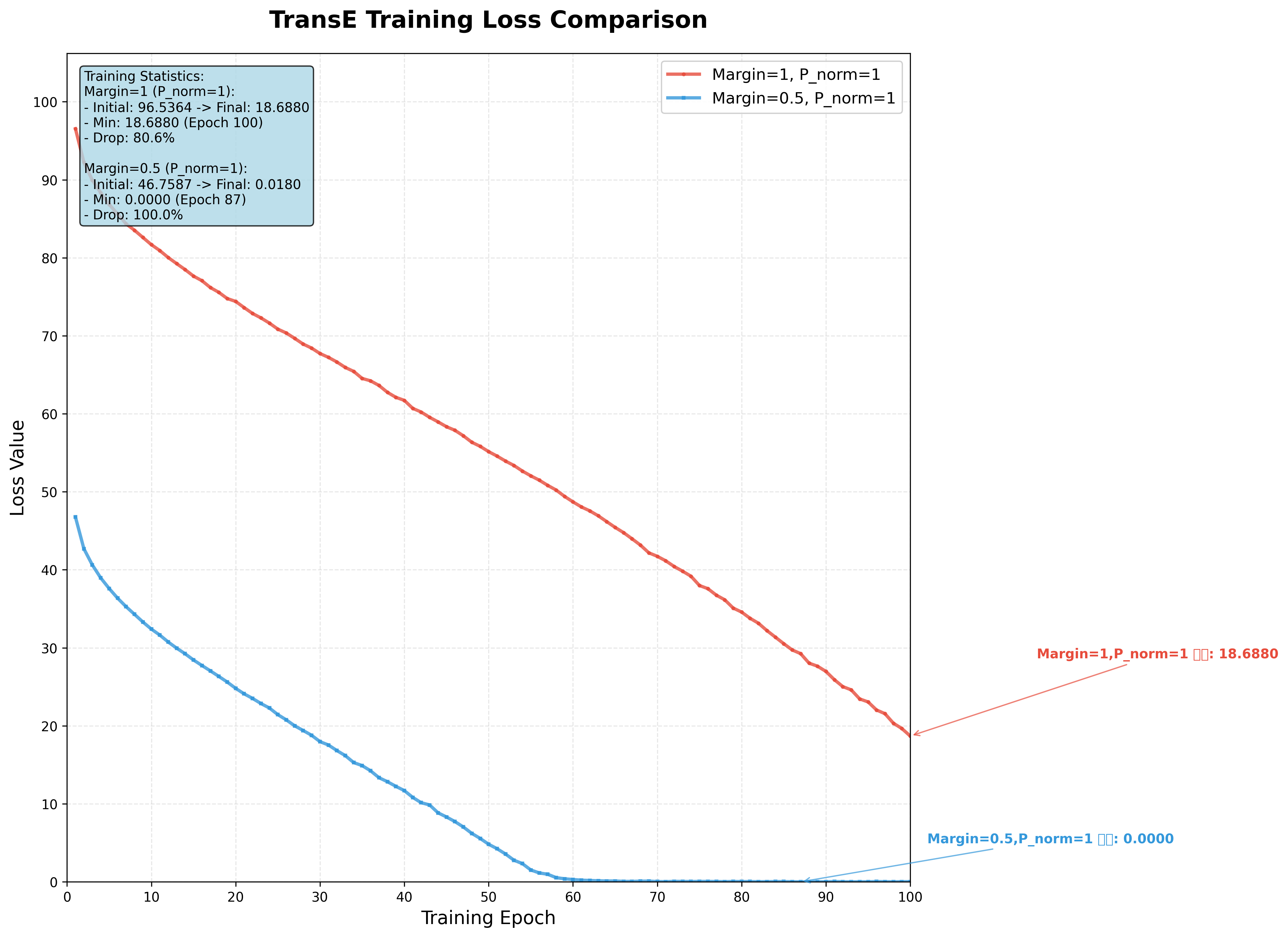
可以明显看出当margain=0.5时，losses收敛更快。

margain=0.5时得到结果如下：

实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）

1. Q30(United States)
2. Q142(France)
3. Q668(India)
4. Q17(Japan)
5. Q38(Italy)

实体Q30（United States），实体Q49(North America),最接近关系（Top5）

1. P30(continent)
2. P289（vessel class）
3. P530（diplomatic relation)
4. P1346(winner)
5. P598(commander of (DEPRECATED))

margain=0.5模型运行结果与margain=1模型运行结果相似，在预测实体Q30（United States），关系P36(capital)，最接近尾实体（Top5）时，排第一的都是United States，预测实体Q30（United States），实体Q49(North America),最接近关系（Top5）时，排第一的也都是continent。