LeetCode 391：完美矩形

问题本质：精确覆盖的两个核心条件

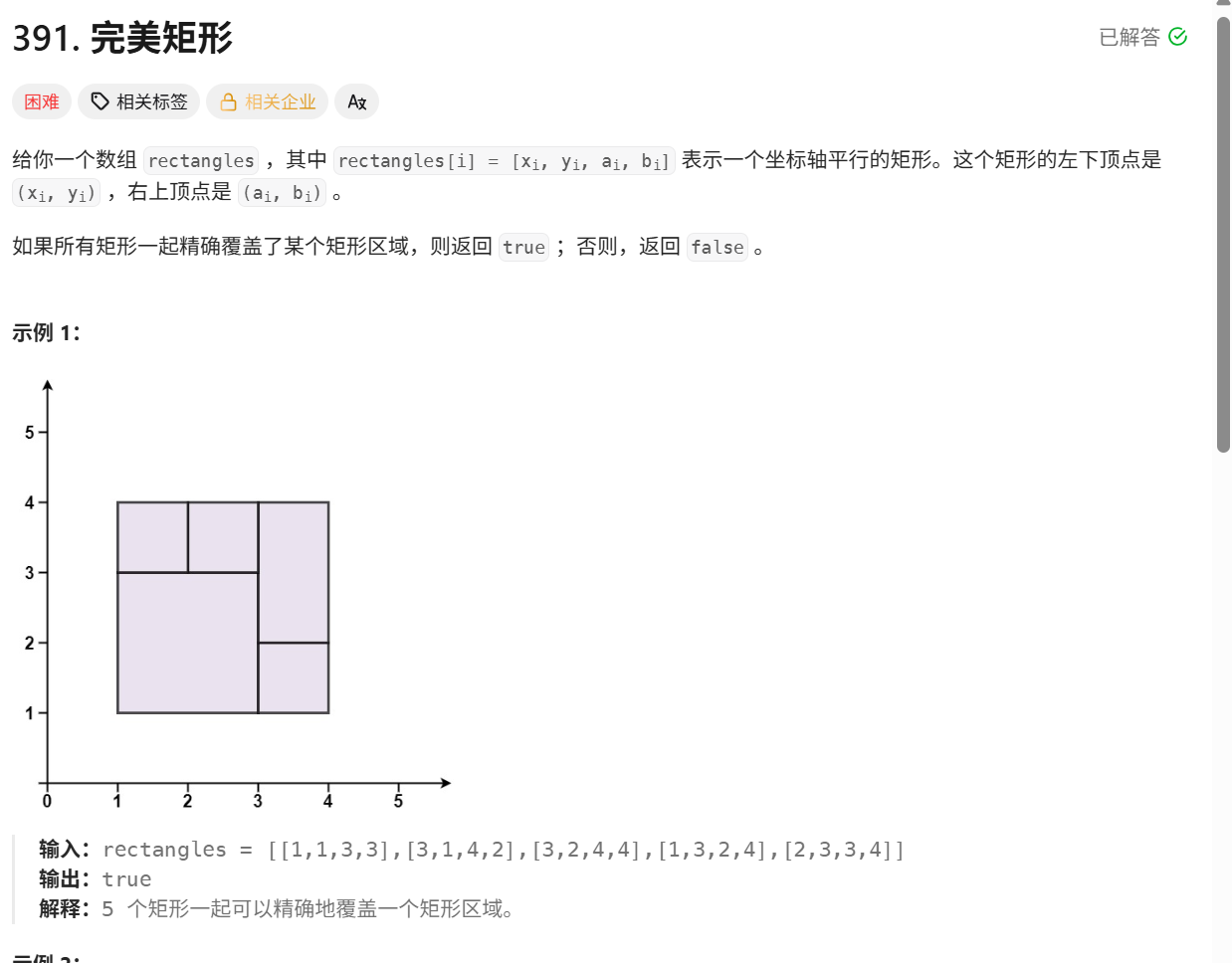
给定若干轴对齐的小矩形，判断它们是否能恰好覆盖一个大矩形（无重叠、无间隙）。需满足：

1. 面积守恒：所有小矩形的面积和等于大矩形的面积。
2. 顶点唯一：除大矩形的4个顶点外，其他顶点必须出现偶数次（重叠时顶点会被覆盖两次，间隙则会导致顶点缺失）。

核心思路：面积 + 顶点统计

1. 面积校验

• 遍历所有小矩形，计算 大矩形的边界（最小左边界 left、最小下边界 bottom、最大右边界 right、最大上边界 top）。
• 计算 小矩形总面积 和 大矩形面积，若不相等，直接返回 false（存在间隙）。

2. 顶点校验

• 用哈希表统计所有小矩形的 4个顶点（左下、左上、右下、右上）的出现次数。
• 大矩形的4个顶点必须仅出现1次（唯一角），其余顶点必须出现偶数次（重叠抵消）。

算法步骤详解

步骤 1：计算大矩形边界与面积

int left = Integer.MAX_VALUE;   // 初始为极大值，确保被更新
int bottom = Integer.MAX_VALUE; 
int right = Integer.MIN_VALUE;  // 初始为极小值，确保被更新
int top = Integer.MIN_VALUE;    
long sumArea = 0;               // 小矩形总面积

for (int[] rect : rectangles) {
    int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
    // 更新大矩形边界
    left = Math.min(left, x1);
    bottom = Math.min(bottom, y1);
    right = Math.max(right, x2);
    top = Math.max(top, y2);
    // 累加小矩形面积
    sumArea += (long)(x2 - x1) * (y2 - y1);
}

// 大矩形面积
long totalArea = (long)(right - left) * (top - bottom);
if (sumArea != totalArea) {
    return false; // 面积不等，直接失败
}

步骤 2：统计顶点出现次数

用哈希表记录每个顶点的出现次数（顶点用 (x, y) 唯一标识，通过位运算转换为 long 键）：

Map<Long, Integer> pointCount = new HashMap<>();

for (int[] rect : rectangles) {
    int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
    // 四个顶点：左下、左上、右下、右上
    addPoint(pointCount, x1, y1);
    addPoint(pointCount, x1, y2);
    addPoint(pointCount, x2, y1);
    addPoint(pointCount, x2, y2);
}

// 辅助方法：将(x,y)转换为唯一long键
private long getKey(int x, int y) {
    return (long)x << 32 | (y & 0xFFFFFFFFL); // x左移32位，y存低32位
}

// 辅助方法：更新顶点计数
private void addPoint(Map<Long, Integer> map, int x, int y) {
    long key = getKey(x, y);
    map.put(key, map.getOrDefault(key, 0) + 1);
}

步骤 3：校验顶点规则

1. 大矩形的4个顶点必须仅出现1次：

   int[][] corners = {
       {left, bottom},  // 左下
       {left, top},     // 左上
       {right, bottom}, // 右下
       {right, top}     // 右上
   };
   
   for (int[] corner : corners) {
       int x = corner[0], y = corner[1];
       long key = getKey(x, y);
       Integer cnt = pointCount.get(key);
       if (cnt == null || cnt != 1) {
           return false; // 顶点不存在或次数不对
       }
       pointCount.put(key, cnt - 1); // 次数减为0（后续统一校验偶数）
   }
   

2. 所有顶点次数必须为偶数（包括大矩形顶点减为0的情况）：

   for (int count : pointCount.values()) {
       if (count % 2 != 0) {
           return false; // 存在奇数次顶点，说明重叠或缺失
       }
   }
   

完整代码（Java）

import java.util.HashMap;
import java.util.Map;

class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        if (rectangles == null || rectangles.length == 0) {
            return false;
        }

        // 步骤1：计算大矩形的边界和总面积
        int left = Integer.MAX_VALUE;
        int bottom = Integer.MAX_VALUE;
        int right = Integer.MIN_VALUE;
        int top = Integer.MIN_VALUE;
        long sumArea = 0;

        for (int[] rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
            left = Math.min(left, x1);
            bottom = Math.min(bottom, y1);
            right = Math.max(right, x2);
            top = Math.max(top, y2);
            sumArea += (long)(x2 - x1) * (y2 - y1);
        }

        // 校验面积是否相等
        long totalArea = (long)(right - left) * (top - bottom);
        if (sumArea != totalArea) {
            return false;
        }

        // 步骤2：统计所有顶点的出现次数
        Map<Long, Integer> pointCount = new HashMap<>();
        for (int[] rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
            addPoint(pointCount, x1, y1);
            addPoint(pointCount, x1, y2);
            addPoint(pointCount, x2, y1);
            addPoint(pointCount, x2, y2);
        }

        // 步骤3：校验大矩形的四个顶点（必须出现1次，然后次数减为0）
        int[][] corners = {
            {left, bottom},
            {left, top},
            {right, bottom},
            {right, top}
        };

        for (int[] corner : corners) {
            int x = corner[0], y = corner[1];
            long key = getKey(x, y);
            Integer cnt = pointCount.get(key);
            if (cnt == null || cnt != 1) {
                return false;
            }
            pointCount.put(key, cnt - 1); // 次数减为0
        }

        // 步骤4：校验所有顶点的次数是否为偶数
        for (int count : pointCount.values()) {
            if (count % 2 != 0) {
                return false;
            }
        }

        return true;
    }

    private long getKey(int x, int y) {
        return (long)x << 32 | (y & 0xFFFFFFFFL);
    }

    private void addPoint(Map<Long, Integer> map, int x, int y) {
        long key = getKey(x, y);
        map.put(key, map.getOrDefault(key, 0) + 1);
    }
}

复杂度分析

• 时间复杂度：O(n)，n 是小矩形数量。遍历矩形（O(n)）、统计顶点（O(n)，每个矩形4个顶点）、校验顶点（O(n)，顶点数最多为 4n，但哈希表遍历是线性的）。
• 空间复杂度：O(n)，哈希表最多存储 4n 个顶点（实际远小于，因为大量顶点会重复）。

示例验证

• 示例1：面积相等，大矩形顶点各出现1次，其余顶点偶数次 → 返回 true。
• 示例2：存在间隙，面积虽相等，但顶点次数不满足 → 返回 false。
• 示例3：存在重叠，某顶点出现奇数次 → 返回 false。

该方法通过面积和顶点的双重约束，高效判断完美覆盖，是处理几何覆盖问题的经典思路。