目录

一、前言

二、算法思想

三、图解

四、测试

 五、优化--队列优化

 六、负权回路

七、源码

一、前言

上篇文章中提到对于带有负权值的边的图，Dijkstra算法是不能求出最小生成路径的，那么对于带有负权值的边的图我们该如何求出来它的最小生成路径呢？接下来就该介绍Bellman-Ford算法

二、算法思想

Bellman-Ford是一种比较暴力的求解更新：

该算法会对图进行最多 V−1 次迭代，其中 V 表示图中顶点的数量。之所以是 V−1次，其原因我们将在后文详细解释。

在每一次迭代过程中，算法会遍历图中的所有边，并对每条边的终点执行“松弛”操作。所谓松弛，是指：对于一条从顶点 uu 指向顶点 vv 的边，检查从源点 ss 到 uu 的当前最短距离加上边 (u,v)(u,v) 的权重，是否小于从 ss 到 vv 的当前已知距离。如果更小，就更新 vv 的最短距离为这个更优的值；否则，保持原距离不变。通过这种方式，逐步优化并逼近每个顶点的真实最短路径。

值得注意的是，如果在某次完整迭代中，没有任何顶点的最短距离被更新，说明所有最短路径已经确定，算法可以提前终止。这一特性也为后续的性能优化提供了可能。

Dijkstra算法

• 采用贪心策略： 每一步都选择当前距离源点最近的未处理顶点（"最短路径优先"），并认为该顶点的最短路径已最终确定。这个过程类似于涟漪扩散，从源点逐步向外扩展。

• 无法检测负权环。若存在负权环，算法可能陷入死循环或给出错误结果。

• 使用优先队列优化时：O((|V|+|E|)log|V|) 适用于稠密图（边数接近 |V|² 时效率较高）

• Dijkstra算法 需要借助优先队列（最小堆） 高效选择顶点，实现较复杂。

• 在非负权图中能快速收敛，每个顶点只需处理一次。

• 适用于路由导航、物流规划等非负权场景，是实际应用中更常用的选择。

Bellman-Ford算法

• 采用动态规划思想： 通过 |V|-1 轮全局松弛操作（每轮遍历所有边），逐步逼近最优解。不假设局部最优解即全局最优，而是通过多轮迭代保证全局收敛。
• 通过额外一轮松弛操作可精准检测负权环：若第 |V| 轮松弛后距离仍可优化，则证明存在负权环。
• 固定为 O(|V|·|E|) 在稀疏图（|E| << |V|²）中可能更高效
• 仅需简单循环嵌套：外层 |V|-1 次，内层遍历所有边，实现更简单。
• 需要完整的 |V|-1 轮迭代才能保证收敛，可能存在冗余计算。

• 专为解决金融套利检测、含负权边的网络建模等特殊场景设计，例如：

   
  • 货币汇率套利（负权环=无限套利机会）
  • 游戏中的伤害转移路径（负权表示增益效果）
  • 带惩罚机制的网络路由

三、图解

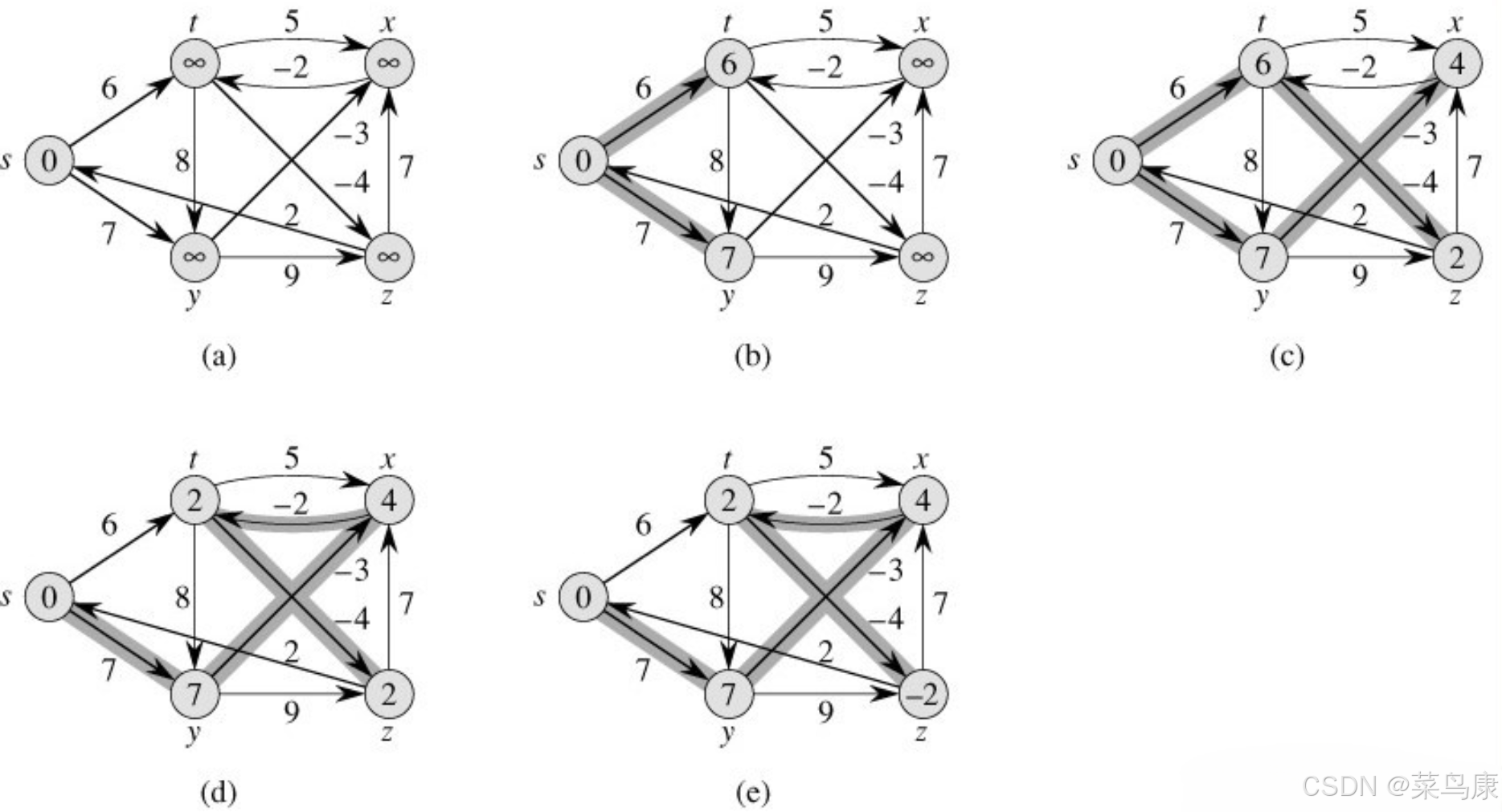
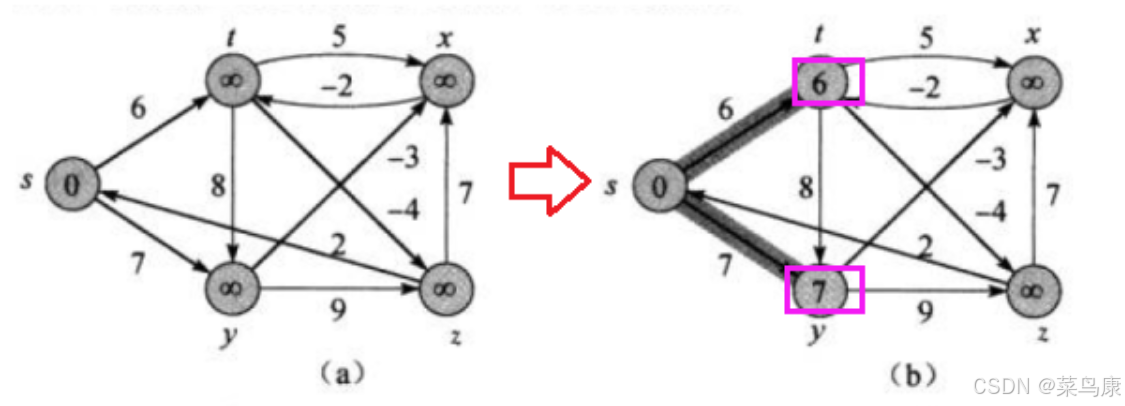
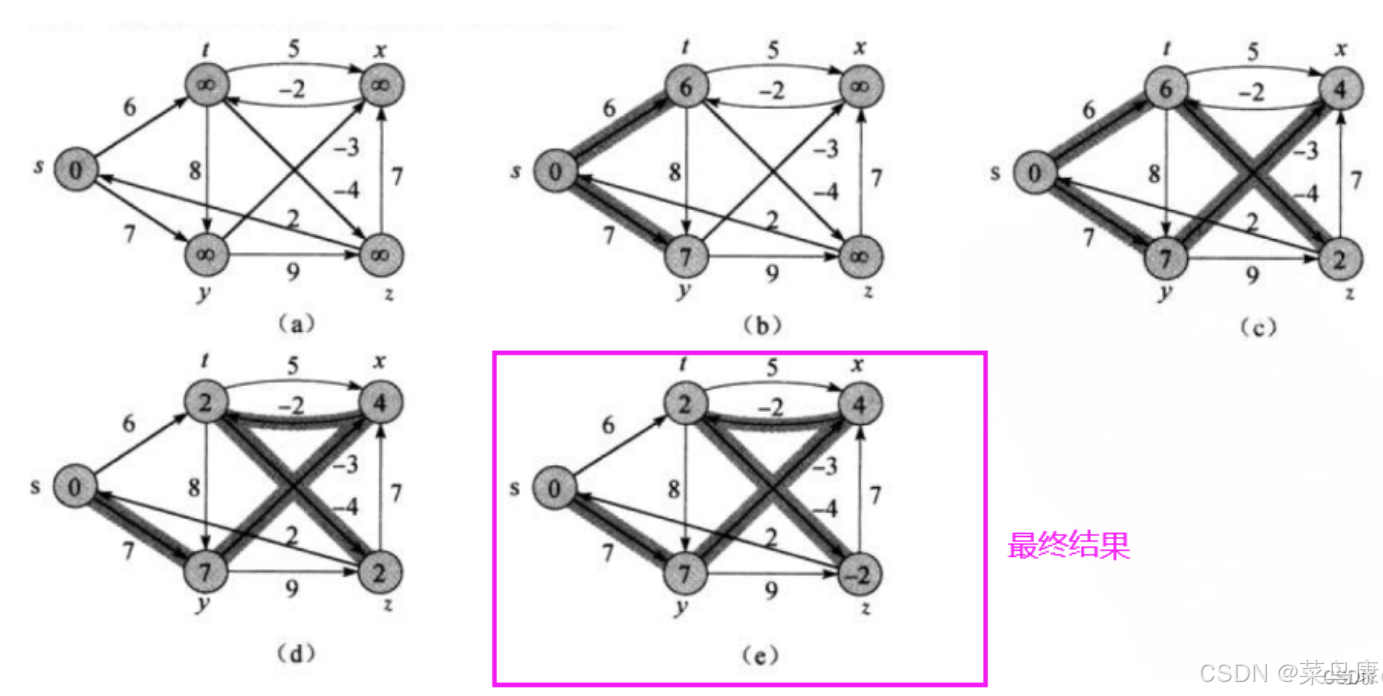
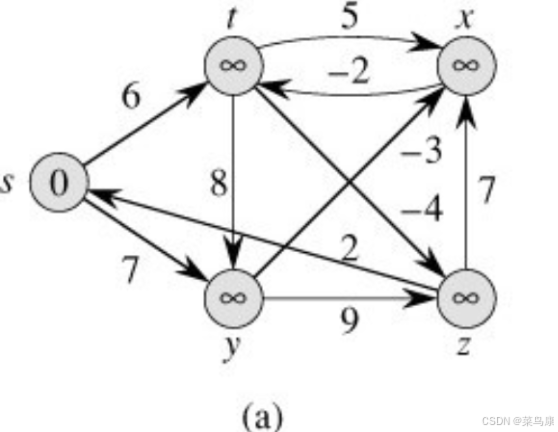
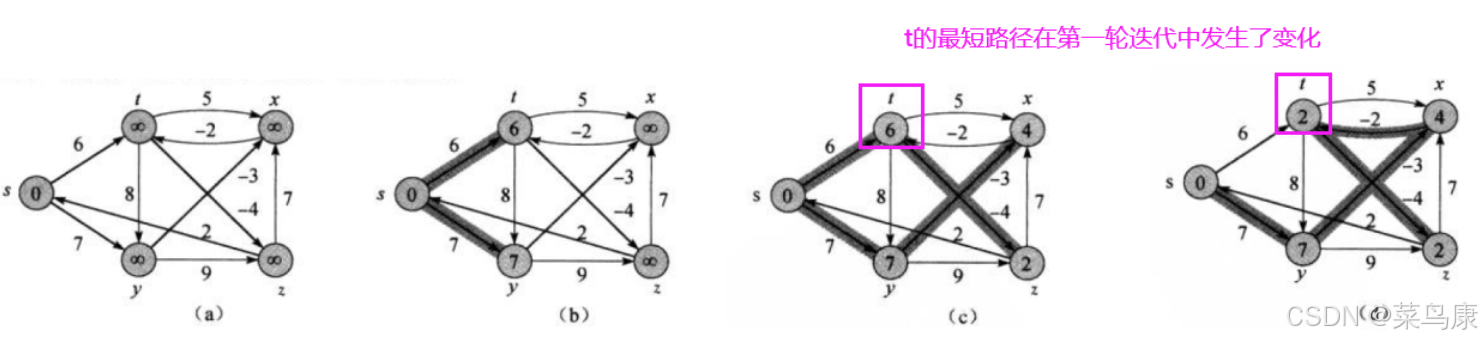
 首先，起始状态时，s位为源点，对s的相邻顶点进行松弛（当然实际中应该是按照顶点在邻接矩阵里面存储的顺序去遍历的，那其实这个图和我们上一篇文章讲Dijkstra算法的那个图顶点都是一样的，只是权值不同，所以下面我们就按之前的存储顺序去走） 那s的话这里他连出去的两条边肯定都会更新（因为源节点s到当前结点u（这里就是s) 的代价与u 到v 的代价之和是否比原来s 到v 的代价更小） 那第一次松弛之后如下：

然后对y的相邻顶点进行松弛如下

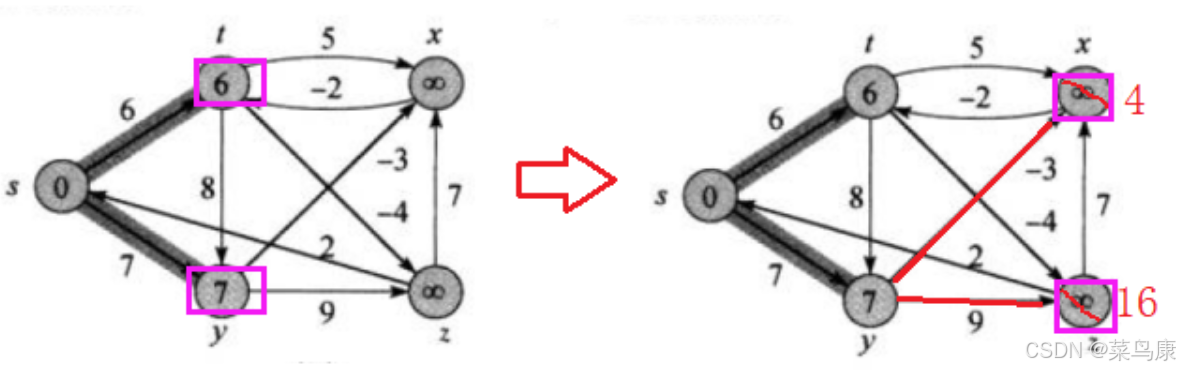
接着是z

z只连出去一条边z->x，但是这里不会更新，因为s->z+z->x的距离大于目前s->x的距离 接着是t

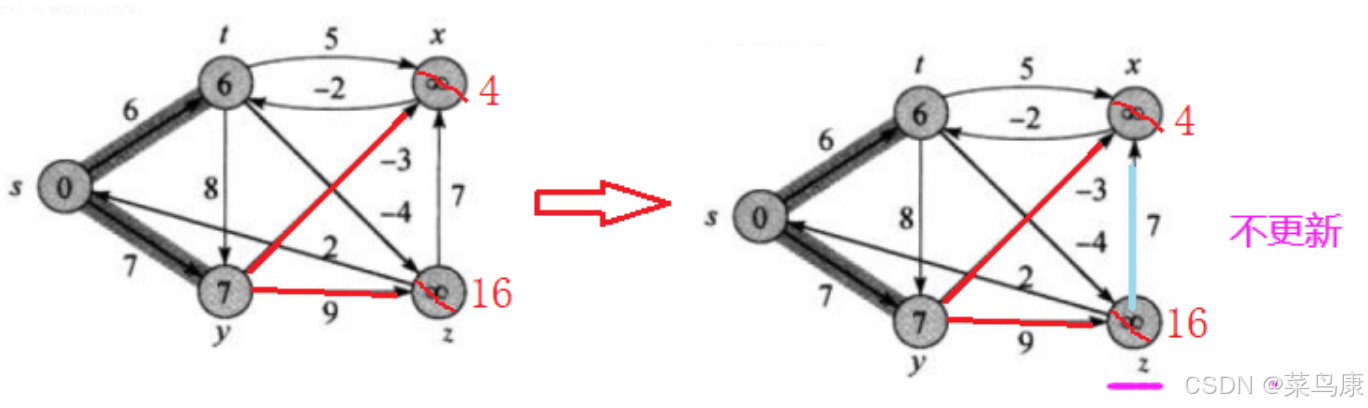
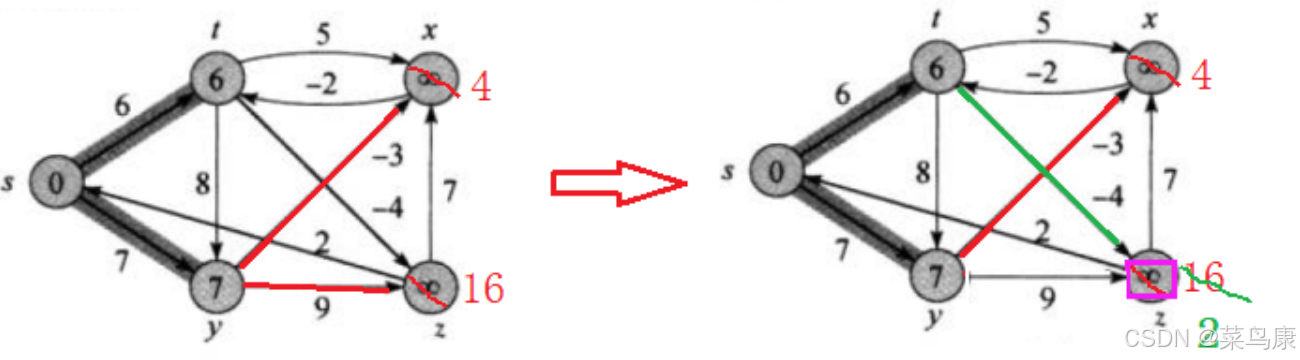 t连出去了两条t->z和t->x，只更新t->z，那之前的s->y->z(16)就不再是z目前的最短路径了（当然实际写代码中的话我们的两个数组：路径距离/权值的数组dist 和 存储路径的数组pPath就也需要相应的修改） 最后是x

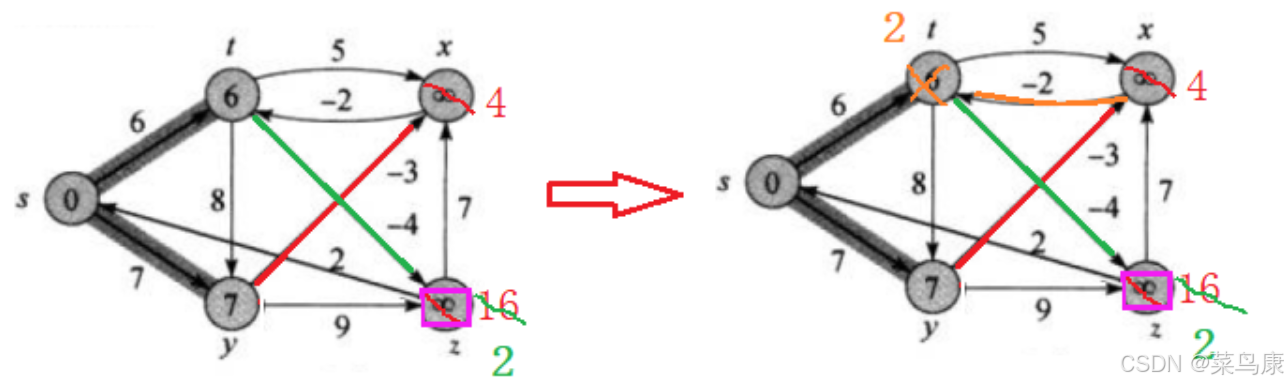
x只连出去一条边x->t，进行更新

那现在其实一趟迭代就完成了，所有顶点的相邻顶点都完成了一次松弛

我们现在得到的是这样一个样子：

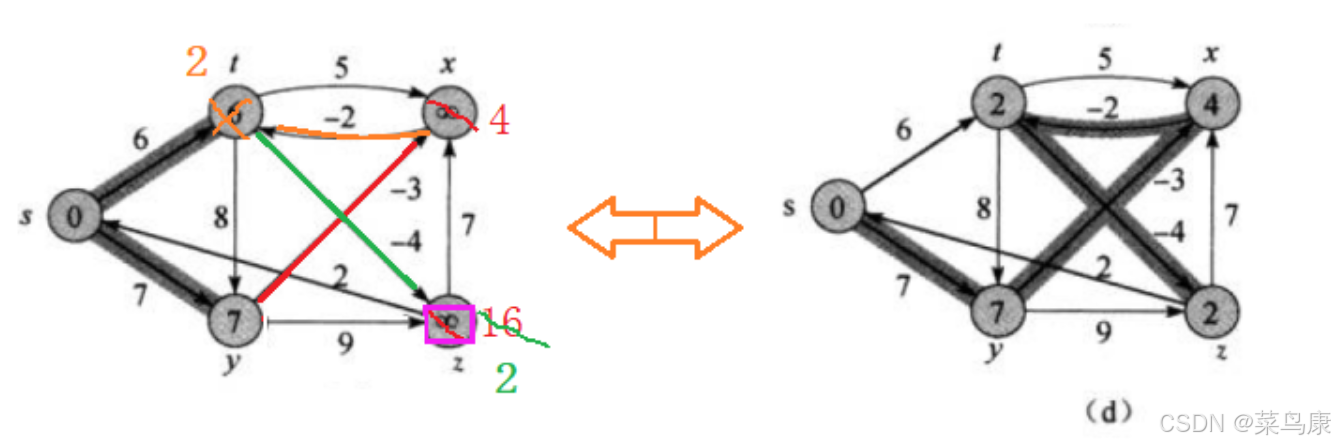
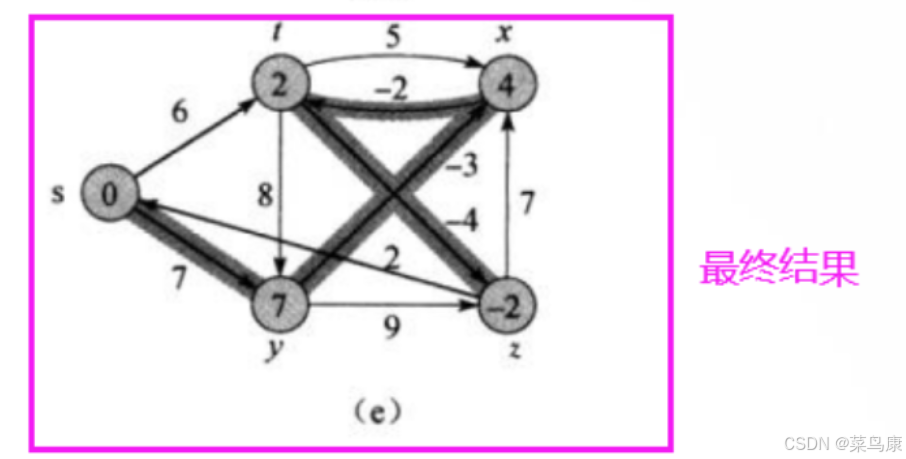
 其实就是最开始给大家看的图里面倒数第二个

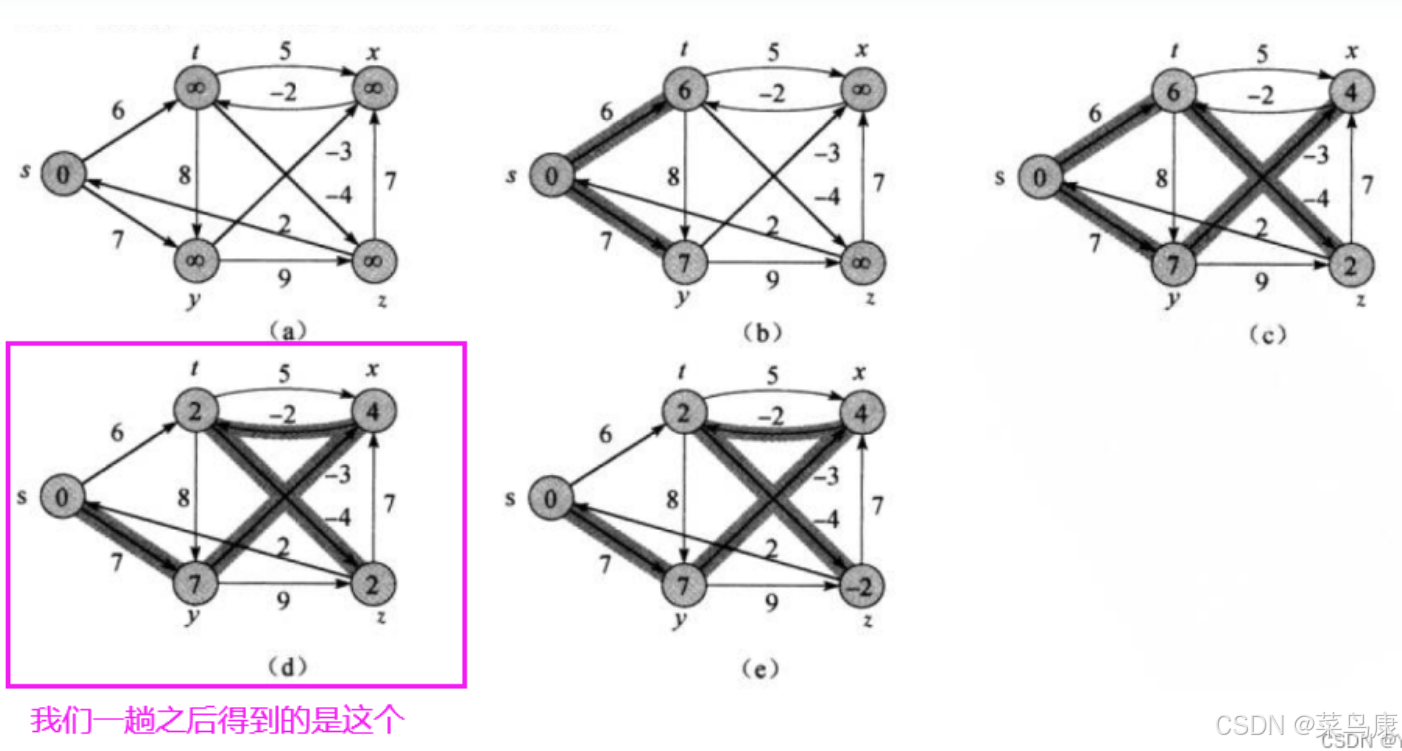
可是最后一幅才是最终结果啊：

是的，所以我们上面也说了： Bellman-Ford算法是比较暴力的把所有的边都更新（即先后对所有的顶点的相邻顶点进行松弛），而不像Dijkstra算法的贪心那样每次选的都是最短的，也因此它一遍过后可能得不出最短的路径，可能需要进行多次迭代

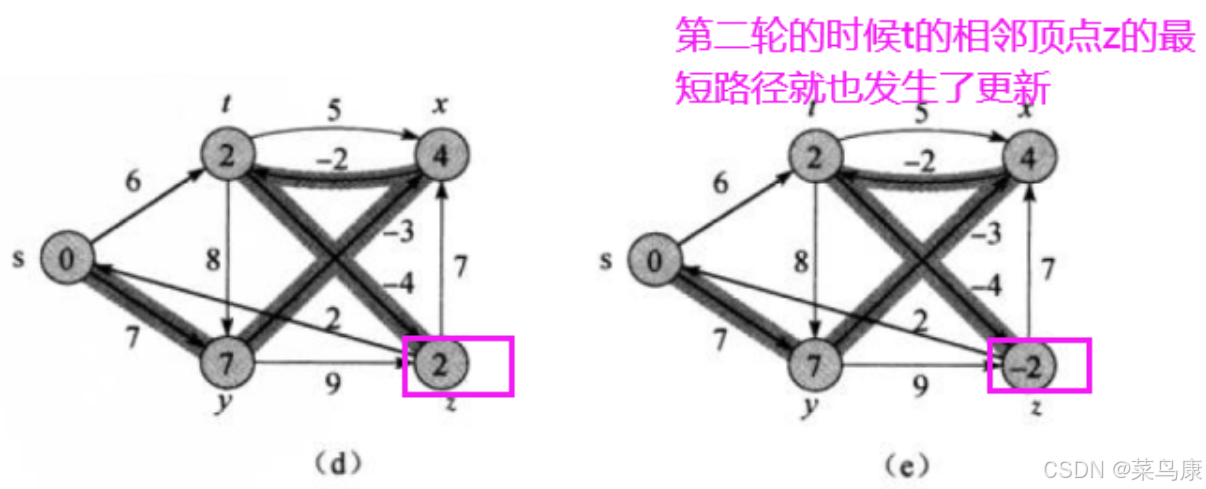
 下面进行第二次迭代：

首先第一个还是s顶点，那这里没有边需要更新； 然后是y，也没有边更新； 接着z，也没有更新； 再下面t，更新一条：现在t的最短路径是2，t->z是-4，所以z的最短路径更新为-2

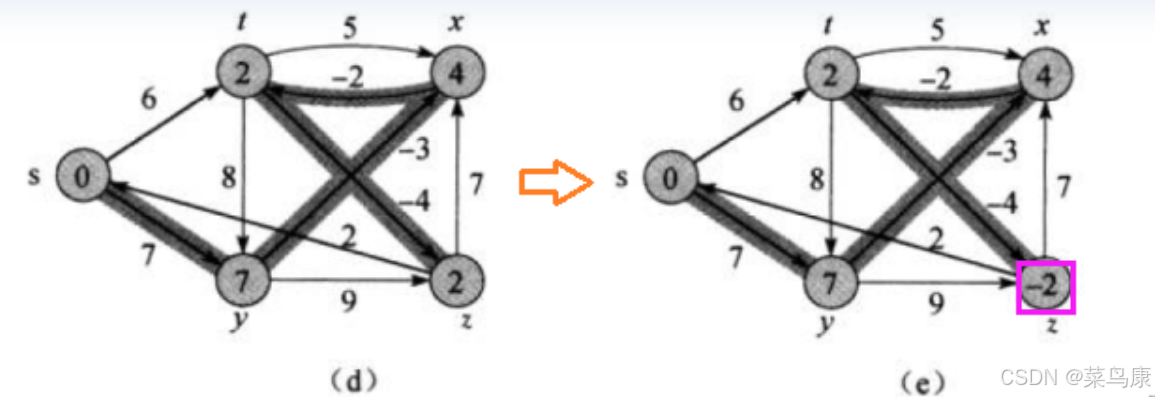
我们看到这次边并没有变化，只是权值更新了； 因为上一轮z的最短路径确定为s->t->z：2（此时t的最短路径是s->t：6）之后，t的最短路径又被更新成了s->y-x-t：2 t的最短路径变了，导致z的最短路径也变了，但是在第二轮才更新出来 最后顶点x，也没有边更新

 此时就得到了最终结果，所以我们看到这里这个图起始更新了两轮（后面代码写出来我们也可以验证一下是不是两轮）就得到了最终结果，后续即使再进行迭代，也不会有新的路径更新了。 所以我们说了可以提前结束，不一定非要迭代V-1 次， V 是图中顶点的数量

因为如果一个图有V个顶点，那图中路径最多也只经过V-1条边，所以V-1次迭代可以保证所有顶点的最短路径被正确地计算更新。 当然我们可以通过判断提前结束。这就是为什么要迭代V-1次。 

四、代码实现

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)

• const V& src：源顶点（起点），类型为 V（可能是 string, int 等）。
• vector<W>& dist：输出参数，存储从 src 到各个顶点的最短距离。W 是权值类型（如 int, double）。
• vector<int>& pPath：输出参数，记录每个顶点在最短路径上的“前驱”（父节点），用于重构路径。

---

size_t n = _vertexs.size();//获取顶点数量
size_t srci = GetVertexIndex(src);//获取源点索引
dist.resize(n, MAX_W);//存储源点到各个顶点的最小权重，进行初始化
pPath.resize(n, -1);//存储最短路径的具体路径，初始化为 -1，表示所有顶点都没有前驱（即路径未确定）。
//W() 是 W 类型的默认构造函数，通常为 0（比如 int() 就是 0）。
dist[srci] = W();//dist[srci] = 0;源点到自己的距离为 0。

初始化操作

---

for (size_t k = 0; k < n; ++k)
{
    bool update = false;
    cout << "更新第:" << k << "轮" << endl;

• Bellman-Ford 的核心思想是：对所有边进行最多 n-1 次松弛操作，就能得到最短路径。
• 这里循环 n 次（0 到 n-1），是因为第 0 轮是初始化后的第一次更新。
• update 标记本轮是否有任何距离被更新。如果没有，说明已经收敛，可以提前退出。
• 输出当前是第几轮，便于调试。

---

    for (size_t i = 0; i < n; ++i)
    {
        for (size_t j = 0; j < n; ++j)
        {
            if (_matrix[i][j] != MAX_W && dist[i] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
            {
                update = true;
                dist[j] = dist[i] + _matrix[i][j];
                pPath[j] = i;
            }
        }
    }

• 双重循环遍历图中所有可能的边 (i, j)。

---

_matrix[i][j] != MAX_W      // 存在边 i -> j
&& dist[i] != MAX_W         // 当前已知从 srci 到 i 的最短距离
&& dist[i] + _matrix[i][j] < dist[j]  // 通过 i 到 j 更短

如果满足以上三个条件，说明可以通过 i 改善 j 的最短距离，进行松弛操作：

• update = true;：标记本轮有更新。
• dist[j] = dist[i] + _matrix[i][j];：更新最短距离。
• pPath[j] = i;：记录 j 的前驱是 i，用于路径还原。

---

    if (update == false)
    {
        break;
    }

提前终止优化

• 如果某一轮中没有任何边被松弛，说明最短路径已经收敛，后续轮次不会再有变化。
• 提前退出，提高效率。
• 最坏情况下仍需 n-1 轮，但最好情况可能只需几轮。

---

四、测试

还是使用我们上面图解的图来做测试

void TestGraphBellmanFord()
	{
		const char* str = "syztx";
		Graph<char, int, INT_MAX, true> g(str, strlen(str));
		g.AddEdge('s', 't', 6);
		g.AddEdge('s', 'y', 7);
		g.AddEdge('y', 'z', 9);
		g.AddEdge('y', 'x', -3);
		//g.AddEdge('y', 's', 1); // 新增
		g.AddEdge('z', 's', 2);
		g.AddEdge('z', 'x', 7);
		g.AddEdge('t', 'x', 5);
		//g.AddEdge('t', 'y', -8); //更改
		g.AddEdge('t', 'y', 8);

		g.AddEdge('t', 'z', -4);
		g.AddEdge('x', 't', -2);
		vector<int> dist;
		vector<int> parentPath;
		g.BellmanFord('s', dist, parentPath))
		g.PrintShortPath('s', dist, parentPath);
	}

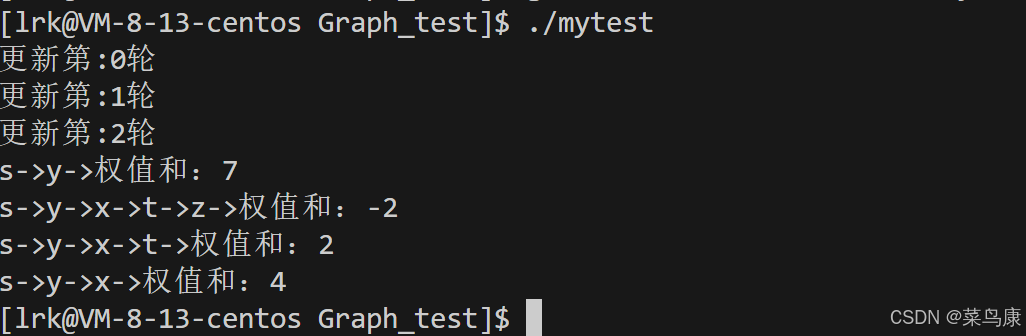
 运行结果如下，可以看到结果正如我们之前流程中的那样

 

 五、优化--队列优化

西南交通大学的段凡丁于1994年提出了用队列来优化的算法：

松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上。 通过使用队列来存储需要进行松弛操作的顶点，可以减少不必要的重复操作。在每次迭代中，只需要对队列中的顶点进行松弛操作，而不用遍历整个图。

就比如我们上面那个图的例子，它其实只有前两轮进行了更新，而且第二轮的时候只对结点t进行了松弛更新

为什么呢？ 因为第一轮t的最短路径更新为s->t(6)之后，后面又变成了s->y-x-t(2) 

 那它就可能影响它的相邻顶点的最短路径

 而除了t之外的其它顶点第二轮并没有真正松弛更新，虽然进行了判断

所以就可以进行队列优化：

搞一个队列，第一轮让所有顶点都入队列，第二轮就只让第一轮更新出更短路径的顶点入队列（后续也是如此），只对队列中的顶点进行松弛操作，就可以避免冗余计算。

 六、负权回路

虽然Bellman-Ford算法可以解决负权图的单源最短路径问题，但是对于图中有负权回路/环（即图中存在环/回路，且环的权值之和为负值）的情况，Bellman-Ford算法也无能为力，在存在负权回路的情况下，理论上可以通过绕这个环路无数次来不断减少路径的总权重，从而使得路径权重趋于负无穷大。这意味着，在这种情况下，“最短路径”的概念变得没有意义，因为总是可以找到更“短”的路径。

在实际中我们可以考虑检测以下这种情况

其实很好办： 如果在进行了n-1次迭代之和还能更新，就是带负权回路的情况 因为如果不带负权回路的情况，最多迭代n-1次就可以得到最终结果

for (size_t i = 0; i < n; ++i)
{
    for (size_t j = 0; j < n; ++j)
    {
        if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
        {
            return false;
        }
    }
}

负权回路检测

• 在完成最多 n-1 轮松弛后，理论上最短路径已确定。
• 如果还能继续松弛（即 dist[i] + w < dist[j] 成立），说明存在负权回路。
• 因为负权回路可以无限绕圈使路径越来越短，最短路径无解。
• 此时返回 false，表示算法失败。

七、源码

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
		{
			size_t n = _vertexs.size();
			size_t srci = GetVertexIndex(src);

			// vector<W> dist,记录srci-其他顶点最短路径权值数组
			dist.resize(n, MAX_W);

			// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组
			pPath.resize(n, -1);

			// 先更新srci->srci为缺省值
			dist[srci] = W();

			//cout << "更新边：i->j" << endl;


			// 总体最多更新n轮
			for (size_t k = 0; k < n; ++k)
			{
				// i->j 更新松弛
				bool update = false;
				cout << "更新第:" << k << "轮" << endl;
				for (size_t i = 0; i < n; ++i)
				{
					for (size_t j = 0; j < n; ++j)
					{
						// srci -> i + i ->j
						if (_matrix[i][j] != MAX_W && dist[i] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
						{
							update = true;
							//cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;
							dist[j] = dist[i] + _matrix[i][j];
							pPath[j] = i;
						}
					}
				}

				// 如果这个轮次中没有更新出更短路径，那么后续轮次就不需要再走了
				if (update == false)
				{
					break;
				}
			}


			// 还能更新就是带负权回路
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					// srci -> i + i ->j
					if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
					{
						return false;
					}
				}
			}

			return true;
		}

---

感谢阅读！