一. ARIMA模型

ARIMA（Autoregressive Integrated Moving Average）全称自回归积分滑动平均模型，专门用于时间序列预测，核心解决 3 类问题：

1. 自回归（AR）：用历史数据的线性组合预测未来（依赖自身过去值）。
2. 差分（I）：将非平稳序列转化为平稳序列（解决趋势、周期性问题）。
3. 滑动平均（MA）：用历史预测误差的线性组合修正预测（依赖过去的误差）。

1. 平稳性检测与差分处理

一阶差分的定义（超简单）

一阶差分 = 后一个数据 - 前一个数据

一阶差分的核心作用：让数据变 “平稳”（ARIMA 的前提）

ARIMA 模型有个硬性要求：输入的数据必须是 “平稳序列”。
什么是平稳序列？简单说就是：

• 没有明显的上升 / 下降趋势（比如你的原始销量从 120 涨到 255，明显在上升，这叫 “非平稳”）；
• 波动幅度稳定（不会突然从每月涨 10 变成每月涨 100）。

2. 自相关（ACF）与偏自相关（PACF）图

• ACF（自相关图）：看 “当前值” 和 “滞后值” 的直接 + 间接相关性，主要用来选 q（MA 阶数）；
• PACF（偏自相关图）：看 “当前值” 和 “滞后值” 的直接相关性（排除中间滞后项的干扰），主要用来选 p（AR 阶数）。

自相关是衡量一个时间序列和它自身 “滞后版本” 之间的相关性。

比如你有 36 个月的销量数据（记为sales(1)到sales(36)）：

• 滞后 1 期（lag=1）：比较sales(1)与sales(2)、sales(2)与sales(3)……sales(35)与sales(36)的相关性；
• 滞后 2 期（lag=2）：比较sales(1)与sales(3)、sales(2)与sales(4)……sales(34)与sales(36)的相关性；
• 滞后 k 期（lag=k）：比较第 i 个月和第 i+k 个月的销量相关性。

相关性数值范围是[-1,1]：

• 接近 1：滞后 k 期的两个序列 “同向变动”（比如本月销量高，k 个月后也容易高）；
• 接近 - 1：“反向变动”（本月高，k 个月后可能低）；
• 接近 0：几乎无关联。
• 

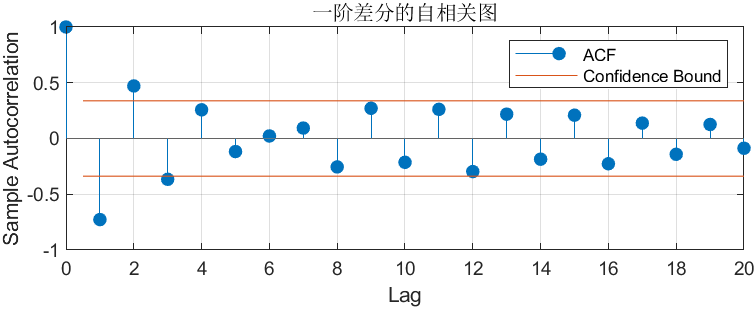
你的代码里对 “一阶差分序列” 画了 ACF 图（autocorr(diff(sales))），输出的图长这样（示意图）：

• 如果 lag=1 的竖线超过红线：说明 “当月销量变化” 和 “上月销量变化” 显著相关；
• 如果 lag=2 的竖线也超过红线：说明和 “上上月变化” 也相关；
• 到某个 lag 后竖线落在红线内：说明更远的滞后项已无显著关联。

• x 轴：滞后阶数（lag=0,1,2,...，通常显示到 10-20 阶）；
• y 轴：自相关系数（上面说的[-1,1]数值）；
• 蓝色竖线：每个滞后阶数对应的自相关系数；
• 红色虚线：置信区间（通常 95%）—— 超过这条线的系数，说明 “相关性显著”（不是偶然出现的）。

• 
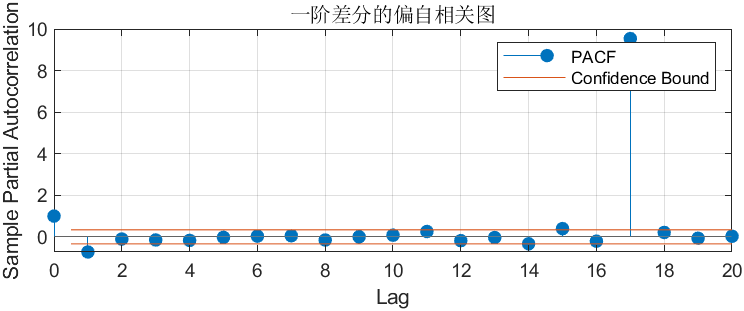
• ACF 看 MA（q）：找 “显著超过置信区间的最大 Lag”；
• PACF 看 AR（p）：找 “显著超过置信区间的最大 Lag”；

步骤	代码操作	原理核心
1. 数据观察	plot(sales)	识别趋势、周期性（判断是否需要差分）
2. 平稳化	diff(sales)	通过差分消除趋势，使序列平稳
3. 定阶	autocorr/parcorr	用 ACF/PACF 选 AR (p) 和 MA (q) 的阶数
4. 建模	arima(p,d,q)	组合 AR、差分、MA 构建模型
5. 拟合	estimate(model, sales)	用历史数据估计模型参数（φ, θ）
6. 预测	forecast(fitModel, 6)	递推计算未来值，结合 AR 和 MA 逻辑

二. LSTM模型 

LSTM 是一种循环神经网络（RNN）的变体，专门解决时间序列数据的 “长期依赖” 问题（比如用前 5 天的访问量预测第 6 天，需要模型记住前 5 天的关联）。

2. 对模型的具体影响（分场景）

场景 1：数据有 “长期趋势”（如你的模拟数据）

场景 2：数据有 “周期性规律”（如每周销量高峰）

场景 3：数据波动大、噪声多

3. 如何选择步长？（3 个实用方法）

• RMSE（均方根误差）：衡量预测值与真实值的平均偏差，值越小说明预测越准；

  滑动窗口步长（sequenceLength）的影响

  滑动窗口步长（代码中 sequenceLength=5）指用 “前几天的数据” 预测 “后 1 天”，它直接影响模型学习的 “时序关联长度”。以下从原理和场景分析其影响：

  1. 滑动窗口的本质：决定模型 “看多远的历史”

• sequenceLength=5：模型用前 5 天的历史数据预测第 6 天；
• sequenceLength=3：模型用前 3 天的历史数据预测第 4 天；
• 步长越大，模型能看到的历史越长，但也会增加学习难度（需要记住更多关联）。
• 步长太小（如 sequenceLength=2）：
  模型只能看到前 2 天的数据，无法捕捉 “5 天的累加趋势”，预测误差会大；
• 步长适中（如 sequenceLength=5）：
  刚好覆盖 “趋势形成的关键历史”（5 天累加足够形成可见趋势），模型能学习到趋势；
• 步长太大（如 sequenceLength=10）：
  模型需要记住前 10 天的波动，可能因 “噪声过多” 导致过拟合（把波动当趋势学习）。
• 步长 = 7：
  模型用前 7 天数据预测第 8 天，能捕捉 “一周的周期”（如第 7 天是周六，第 8 天是周日，访问量高）；
• 步长 = 5：
  可能错过 “周末高峰” 的周期，导致预测不准。
• 步长太小：模型无法区分 “趋势” 和 “噪声”，容易把噪声当趋势；
• 步长太大：模型会记住过多噪声，导致预测结果波动大，无法捕捉真实趋势。
• 领域知识法：
  如果是 “日访问量”，根据经验选 “1 周（7 天）” 或 “1 个月（30 天）” 的步长；
• 验证法：
  尝试不同步长（如 3、5、7），看测试集 RMSE 哪个最小；
• 自动搜索法：
  用循环遍历步长，结合交叉验证选最优（适合数据量大的场景）。

  代码环节	LSTM 核心逻辑
  滑动窗口构造样本	将时间序列转化为 “历史序列→未来值” 的监督学习对，让 LSTM 学习 “时序关联”
  LSTM 层设计	通过门机制（遗忘 / 输入 / 输出门）控制信息的记忆与遗忘，解决长期依赖问题
  训练过程	前向传播计算预测，反向传播调整门参数和全连接层权重，最小化预测误差
  预测与评估	用训练好的门机制，对新序列预测未来值；用 RMSE 量化误差，可视化验证趋势捕捉能力

三. 朴素贝叶斯分类器模型 

• 理论理解：朴素贝叶斯的核心是贝叶斯定理 + 特征独立性假设
• 实现关键：
  • 计算先验概率：P(Ck)=nknP(C_k) = \frac{n_k}{n} P(Ck​)=nnk​​
  • 计算似然概率：假设高斯分布，用均值和方差描述
  • 预测时选择后验概率最大的类别
  • fitcnb：MATLAB 内置函数，用于训练分类朴素贝叶斯模型
    • 参数：X（特征矩阵）和 y（标签向量）
    • 返回：训练好的模型对象，包含：
      • 先验概率 P (类别)：每个类别的样本占比
      • 条件概率 P (特征 | 类别)：每个特征在每个类别下的分布

四. 卡方检验模型

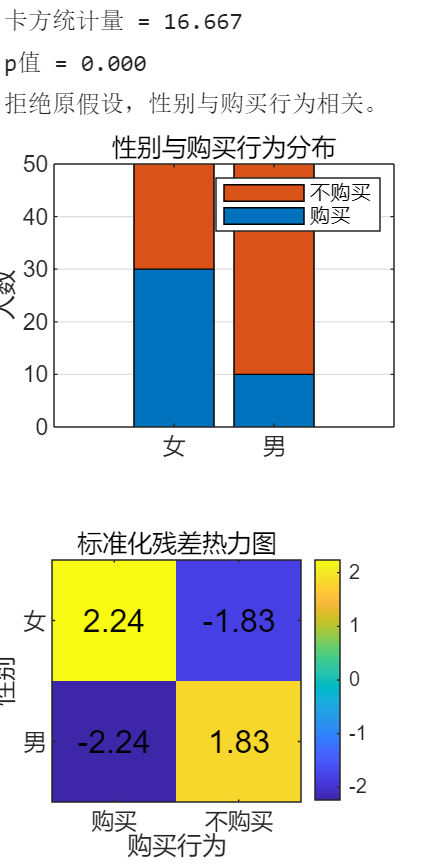
卡方检验（Chi-square Test）是一种基于 “实际观测值” 与 “理论期望值” 差异的统计方法，用于判断两个分类变量是否独立。

• 原假设（H₀）：两个变量独立（无关联）
• 备择假设（H₁）：两个变量不独立（有关联）
• 判断标准：计算 p 值，若 p < 0.05（显著性水平），则拒绝原假设，认为变量相关。