大模型对齐算法(二): TDPO(Token-level Direct Preference Optimization)
TDPO:基于Token级偏好的语言模型优化方法 TDPO(Token-level Direct Preference Optimization)是针对DPO方法在句子级KL散度控制上的局限性提出的改进方案。传统DPO存在KL增长失衡和多样性下降等问题,而TDPO通过将RLHF任务拆分为token级MDP,引入Bellman方程和双向KL约束机制。
TDPO(Token-level Direct Preference Optimization)
1. 研究背景
| 痛点 | 说明 |
|---|---|
| DPO 句子级 KL | 只在完整回答上算 KL,无法细粒度控制逐 token 的偏离。 |
| KL 增长失衡 | 图1 显示,DPO 在 dis-preferred 回答上的 SeqKL 增长更快,导致分布差异越拉越大。 |
| 多样性下降 | 反向 KL 的“mode-seeking”特性限制了生成多样性。 |
2. TDPO 核心思想
- 把 RLHF 任务拆成 token-level MDP
- 状态:prompt + 已生成的 token
- 动作:下一个 token
- 奖励:rt=R([x,y<t],yt)r_t = R([x, y_{<t}], y_t)rt=R([x,y<t],yt)
-
用 Bellman 方程把句子奖励
r(x,y)=∑t=1Tγt−1rtr(x, y)=\sum_{t=1}^{T}\gamma^{t-1} r_tr(x,y)=∑t=1Tγt−1rt -
在 token 上同时引入
- 反向 KL(防止整体偏离)
- 正向 SeqKL(抑制 dis-preferred 回答的 KL 暴涨)
3. 关键公式速览
| 名称 | LaTeX | 说明 |
|---|---|---|
| token 级目标 | maxπθEx,y<t,z[Aπref−βDKL(πθ∥πref)]\max_{\pi_\theta} \mathbb{E}_{x,y_{<t},z} \Big[A^{\pi_{\text{ref}}} - \beta D_{\text{KL}}\bigl(\pi_\theta\|\pi_{\text{ref}}\bigr)\Big]maxπθEx,y<t,z[Aπref−βDKL(πθ∥πref)] | TRPO 风格 |
| 最优策略 | π∗(z,y<t)∝πref(z,y<t)exp(1βQπref(y<t,z))\pi^*(z, y_{<t}) \propto \pi_{\text{ref}}(z, y_{<t})\exp\Bigl(\tfrac{1}{\beta}Q^{\pi_{\text{ref}}}(y_{<t},z)\Bigr)π∗(z,y<t)∝πref(z,y<t)exp(β1Qπref(y<t,z)) | |
| BT-token 模型 | P(y1≻y2,x)=σ (u−δ)P(y_1\succ y_2, x)=\sigma\!\bigl(u-\delta\bigr)P(y1≻y2,x)=σ(u−δ) | |
| uuu 与 δ\deltaδ | u=βlogπθ(y1)πref(y1)−βlogπθ(y2)πref(y2)u=\beta\log\frac{\pi_\theta(y_1)}{\pi_{\text{ref}}(y_1)}-\beta\log\frac{\pi_\theta(y_2)}{\pi_{\text{ref}}(y_2)}u=βlogπref(y1)πθ(y1)−βlogπref(y2)πθ(y2) δ=βDSeqKL(y2)−βDSeqKL(y1)\delta=\beta D_{\text{SeqKL}}(y_2)-\beta D_{\text{SeqKL}}(y_1)δ=βDSeqKL(y2)−βDSeqKL(y1) |
奖励差+KL差 |
4. 损失函数
论文给出 两个版本:
| 版本 | 公式 | 特色 |
|---|---|---|
| TDPO1 | −Elogσ (u−δ)-\mathbb{E}\log\sigma\!\bigl(u-\delta\bigr)−Elogσ(u−δ) | 双向 KL 同时约束 |
| TDPO2 | −Elogσ (u−αδ2)-\mathbb{E}\log\sigma\!\bigl(u-\alpha\delta_2\bigr)−Elogσ(u−αδ2) δ2\delta_2δ2 用 stop-gradient 保护 preferred KL |
防止 preferred 回答 KL 被拉高 |
5. 实验结果
| 数据集 | 指标 | 结论 |
|---|---|---|
| IMDb | Reward vs SeqKL Frontier | TDPO2 优于 DPO、f-DPO,更高奖励 + 更低 KL |
| Anthropic-HH | 对齐准确率 & 熵 | TDPO2 同时提升 准确率 67.3% 和 熵 4.915 |
| MT-Bench | GPT-4 打分 | TDPO2 vs DPO:60.4% 胜 28.8% 平 10.8% 负 |
6. 代码片段(PyTorch)
def tdpo_loss(pi_logits, ref_logits, yw_idxs, yl_idxs,
labels, beta=0.1, alpha=0.5, if_tdpo2=True):
pi_logp = pi_logits.log_softmax(-1).gather(-1, labels.unsqueeze(-1)).squeeze(-1)
ref_logp = ref_logits.log_softmax(-1).gather(-1, labels.unsqueeze(-1)).squeeze(-1)
# per-token KL
kl = (ref_logits.softmax(-1) * (ref_logits.log_softmax(-1) - pi_logits.log_softmax(-1))).sum(-1)
yw_kl, yl_kl = kl[yw_idxs], kl[yl_idxs]
u = beta * (pi_logp[yw_idxs] - ref_logp[yw_idxs]) \
- beta * (pi_logp[yl_idxs] - ref_logp[yl_idxs])
if if_tdpo2:
delta = beta * yl_kl - beta * yw_kl.detach()
else:
delta = beta * yl_kl - beta * yw_kl
loss = -F.logsigmoid(u - alpha * delta)
return loss
7. 总结
TDPO = 把 DPO 的“句子级 KL”拆成“token 级 KL”,再叠一个正向 SeqKL 差分,既对齐人类偏好,又压住 KL 暴涨,实验全面优于 DPO & PPO。
8. 附录
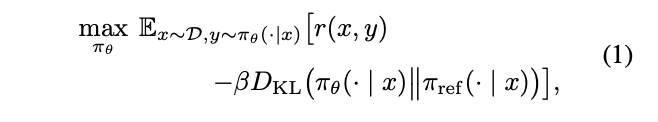
公式1是怎么推导出公式2的呢?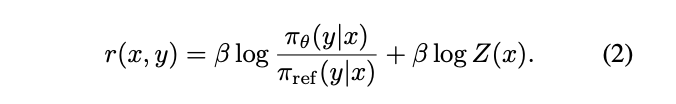
✅ 1 写出带 KL 的目标(公式 1)
maxπθ Ex∼D Ey∼πθ(⋅∣x) [r(x,y)−βDKL(πθ(⋅∣x)∥πref(⋅∣x))]\max_{\pi_\theta}\; \mathbb{E}_{x\sim\mathcal{D}}\; \mathbb{E}_{y\sim\pi_\theta(\cdot|x)}\; \Bigl[r(x,y)-\beta D_{\mathrm{KL}}\bigl(\pi_\theta(\cdot|x)\|\pi_{\mathrm{ref}}(\cdot|x)\bigr)\Bigr]maxπθEx∼DEy∼πθ(⋅∣x)[r(x,y)−βDKL(πθ(⋅∣x)∥πref(⋅∣x))]
✅ 2 把 KL 写成期望形式
DKL(πθ∥πref)=Ey∼πθ[logπθ(y∣x)πref(y∣x)]D_{\mathrm{KL}}\bigl(\pi_\theta\|\pi_{\mathrm{ref}}\bigr) =\mathbb{E}_{y\sim\pi_\theta}\Bigl[\log\frac{\pi_\theta(y|x)}{\pi_{\mathrm{ref}}(y|x)}\Bigr]DKL(πθ∥πref)=Ey∼πθ[logπref(y∣x)πθ(y∣x)]
代入后得到
maxπθ Ex,y∼πθ[r(x,y)−βlogπθ(y∣x)πref(y∣x)]\max_{\pi_\theta}\; \mathbb{E}_{x,y\sim\pi_\theta}\Bigl[ r(x,y)-\beta\log\frac{\pi_\theta(y|x)}{\pi_{\mathrm{ref}}(y|x)} \Bigr]maxπθEx,y∼πθ[r(x,y)−βlogπref(y∣x)πθ(y∣x)]
✅ 3 用变分法求最优策略
令目标函数为
J(π)=Ex,y∼π[r(x,y)−βlogπ(y∣x)πref(y∣x)]J(\pi)=\mathbb{E}_{x,y\sim\pi}\Bigl[r(x,y)-\beta\log\frac{\pi(y|x)}{\pi_{\mathrm{ref}}(y|x)}\Bigr]J(π)=Ex,y∼π[r(x,y)−βlogπref(y∣x)π(y∣x)]
在约束
∑yπ(y∣x)=1\sum_y \pi(y|x)=1∑yπ(y∣x)=1
下对 (π\piπ) 做 拉格朗日乘子法,得到
π∗(y∣x)∝πref(y∣x)exp (1βr(x,y))\pi^*(y|x)\propto\pi_{\mathrm{ref}}(y|x)\exp\!\bigl(\tfrac{1}{\beta}r(x,y)\bigr)π∗(y∣x)∝πref(y∣x)exp(β1r(x,y))
归一化后
π∗(y∣x)=πref(y∣x)exp (1βr(x,y))∑y′πref(y′∣x)exp (1βr(x,y′))\pi^*(y|x)=\frac{\pi_{\mathrm{ref}}(y|x)\exp\!\bigl(\tfrac{1}{\beta}r(x,y)\bigr)} {\sum_{y'}\pi_{\mathrm{ref}}(y'|x)\exp\!\bigl(\tfrac{1}{\beta}r(x,y')\bigr)}π∗(y∣x)=∑y′πref(y′∣x)exp(β1r(x,y′))πref(y∣x)exp(β1r(x,y))
✅ 4 反解奖励函数(得到公式 2)
把上式两边取对数并乘 (β\betaβ):
βlogπ∗(y∣x)πref(y∣x)=βlog1Z(x)+r(x,y)\beta\log\frac{\pi^*(y|x)}{\pi_{\mathrm{ref}}(y|x)} =\beta\log\frac{1}{Z(x)}+r(x,y)βlogπref(y∣x)π∗(y∣x)=βlogZ(x)1+r(x,y)
其中
Z(x)=∑y′πref(y′∣x)exp (1βr(x,y′))Z(x)=\sum_{y'}\pi_{\mathrm{ref}}(y'|x)\exp\!\bigl(\tfrac{1}{\beta}r(x,y')\bigr)Z(x)=∑y′πref(y′∣x)exp(β1r(x,y′))
因此
r(x,y)=βlogπ∗(y∣x)πref(y∣x)+βlogZ(x)r(x,y)=\beta\log\frac{\pi^*(y|x)}{\pi_{\mathrm{ref}}(y|x)}+\beta\log Z(x)r(x,y)=βlogπref(y∣x)π∗(y∣x)+βlogZ(x)
这就是公式 (2)。

火山引擎开发者社区是火山引擎打造的AI技术生态平台,聚焦Agent与大模型开发,提供豆包系列模型(图像/视频/视觉)、智能分析与会话工具,并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长,新用户可领50万Tokens权益,助力构建智能应用。
更多推荐
 已为社区贡献15条内容
已为社区贡献15条内容





所有评论(0)