---

---

论文链接

GitHub链接

本文 “LibraGrad: Balancing Gradient Flow for Universally Better Vision Transformer Attributions” 指出基于梯度的解释方法在 Transformer 中存在梯度流不平衡问题，导致归因不忠实。为此提出 LibraGrad，这是一种通过修剪和缩放反向路径来纠正梯度不平衡的后处理方法，且不改变前向传递和增加计算开销。实验在 8 种架构、4 种模型尺寸和 4 个数据集上展开，采用忠实度、完整性误差和分割 AP 等指标评估，结果表明 LibraGrad 能普遍增强基于梯度的方法，在所有指标上优于现有白盒方法，甚至在无注意力的 MLP-Mixer 架构上也有效，说明平衡梯度流对提升 Transformer 归因效果具有重要意义。

---

摘要-Abstract

Why do gradient-based explanations struggle with Transformers, and how can we improve them? We identify gradient flow imbalances in Transformers that violate FullGradcompleteness, a critical property for attribution faithfulness that CNNs naturally possess. To address this issue, we introduce LibraGrad—a theoretically grounded post-hoc approach that corrects gradient imbalances through pruning and scaling of backward paths, without changing the forward pass or adding computational overhead. We evaluate LibraGrad using three metric families: Faithfulness, which quantifies prediction changes under perturbations of the most and least relevant features; Completeness Error, which measures attribution conservation relative to model outputs; and Segmentation AP, which assesses alignment with human perception. Extensive experiments across 8 architectures, 4 model sizes, and 4 datasets show that LibraGrad universally enhances gradient-based methods, outperforming existing white-box methods—including Transformerspecific approaches—across all metrics. We demonstrate superior qualitative results through two complementary evaluations: precise text-prompted region highlighting on CLIP models and accurate class discrimination between co-occurring animals on ImageNet-finetuned models—two settings on which existing methods often struggle. LibraGrad is effective even on the attention-free MLP-Mixer architecture, indicating potential for extension to other modern architectures.

为什么基于梯度的解释方法在 Transformer 模型上效果不佳，我们又该如何改进呢？我们发现 Transformer 中存在梯度流不平衡的问题，这违反了 FullGrad 完整性——一种 CNNs （卷积神经网络）天然具备的、对于归因忠实性至关重要的属性。为解决这一问题，我们提出了 LibraGrad，这是一种有理论依据的事后方法，通过对反向传播路径进行剪枝和缩放来纠正梯度不平衡，且无需改变前向传播过程或增加计算开销。我们使用三类指标对 LibraGrad 进行评估：一是忠实度，用于量化在对最相关和最不相关特征进行扰动时预测结果的变化；二是完整性误差，衡量归因与模型输出之间的守恒程度；三是分割平均精度（Segmentation AP），评估与人类感知的一致性。在8种架构、4种模型尺寸和4个数据集上进行的大量实验表明，LibraGrad 普遍增强了基于梯度的方法，在所有指标上均优于现有的白盒方法，包括针对 Transformer 的特定方法。我们通过两项互补的评估展示了 LibraGrad 卓越的定性结果：在 CLIP 模型上进行精确的文本提示区域突出显示，以及在 ImageNet 微调模型上对同时出现的动物进行准确的类别区分，而现有方法在这两种情况下往往表现不佳。LibraGrad 甚至在没有注意力机制的 MLP-Mixer 架构上也很有效，这表明它有可能扩展到其他现代架构。

---

引言-Introduction

在深度学习广泛应用的背景下，理解模型决策过程至关重要，输入归因方法有助于实现这一目标。在该部分内容中，作者先强调研究的重要性，再指出当前基于梯度的归因技术在 Transformer 架构中存在的问题，进而提出 LibraGrad 方法，具体内容如下：

1. 研究的重要性：深度学习模型在医疗、自动驾驶等关键领域的应用愈发广泛，理解其决策机制极为关键。输入归因方法可量化单个输入特征对模型输出的影响，是理解模型决策以及构建高级解释技术的基础。
2. 基于梯度的归因技术现状：在 CNN 可解释性领域，基于梯度的归因技术（如 Integrated Gradients 和 FullGrad）为模型解释奠定了基础。然而，Vision Transformers（ViTs）的出现使这些方法暴露出局限性，基于注意力的归因方法有时表现更优。虽然混合方法试图结合梯度和注意力机制，但仍面临缺乏理论基础、难以有效区分类别、产生噪声归因图以及仅适用于特定模型架构等挑战。
3. 问题根源：本文研究发现，基于梯度的方法在 Transformer 中失败的根本原因是反向传播过程中的梯度流不平衡，这会导致不可靠的归因分数。经典 CNNs 通过局部仿射操作自然地保持了适当的梯度流，而现代 Transformer 中的一些组件破坏了这一特性。
4. 提出 LibraGrad 方法：针对上述问题，文章提出 LibraGrad 方法。该方法通过对反向路径进行理论驱动的剪枝和缩放，从源头防止梯度失真，且不改变前向传播过程。实验表明，LibraGrad 不仅能改进所有基于梯度的归因方法，还显示出在梯度流正常时，通用的 Libra FullGrad+ 就能取得优异或可比的性能，凸显了该方法的有效性和优越性。

图1. EVA2-CLIP-Large 模型的定性比较。我们提出的 Libra FullGrad+ 生成了特定提示的归因图（上图），并且在解释“勺子和叉子”提示的模型输出时（下图），与现有方法相比，定位效果有所提升。更多定性示例，请见图2和附录C。

---

背景与相关工作-Background and Related Work

该部分主要介绍了研究相关的背景知识和已有工作，先明确了输入归因方法的数学表达，再分别阐述基于梯度的归因方法、其他归因方法，为后文提出的 LibraGrad 方法做了铺垫，具体内容如下：

1. 输入归因方法的数学表达：对于一个多输出神经模型，设选定的输出函数为 $f:{\mathbb{R}}^n\to \mathbb{R}$，归因方法 $A$ 为每个特征 $x_i$ 生成相关性分数 $A(f)(x{)}_i$.
2. 基于梯度的归因方法
   • Input × Grad：通过 $\text{IxG}(f)(x)=x\odot {\nabla }_{x}f(x)$ 来分配特征相关性，其中 $\odot$ 表示逐元素乘法。
   • FullGrad：在 Input × Grad 基础上进行扩展，不仅包含输入特征，还纳入了神经网络各层的偏置项。其归因图计算式为 $\text{FullGrad}(f)\left(x_0\right)=\text{IxG}(f)\left(x_0\right)+{\sum }_{l=0}^{L-1}{\sum }_{b\in B_l}\text{IxG}\left(f_b\right)(b)$.
   • FullGrad+：进一步扩展 FullGrad，其定义为 $\text{FullGrad+}(f)\left(x_0\right)={\sum }_{l=0}^{L-1}\text{IxG}\left(f_l\right)\left(x_l\right)+{\sum }_{l=0}^{L-1}{\sum }_{b\in B_l}\text{IxG}\left(f_b\right)(b)$，聚合了各层的输入归因图和偏置项的归因图。
   • Integrated Gradients：通过相对于基线输入（如零）计算归因，公式为 $IG(f)(x)=(x-\overline{x})\odot {\int }_{\alpha =0}^1{\nabla }_{x}f(\overline{x}+\alpha (x-\overline{x}))d\alpha$，实际计算中使用50步黎曼求和进行近似。
3. 其他归因方法：将 LibraGrad 应用于多种通用梯度方法，如 HiResCAM、GradCAM+ 、XGradCAM+ ，还应用于专为 Transformer 架构设计的混合注意力-梯度方法，如 GenAtt、TokenTM、AttCAT。同时，为全面评估，还与基于注意力的归因方法（如 RawAtt、Attention Rollout、DecompX）以及基于 Transformer 特定的层相关传播（LRP）技术（如 Conservative-LRP、AttnLRP）进行比较，详细综述见附录E。

---

方法-Method

FullGrad-complete（FG-complete）

• 定义：若对于所有 $x\in {\mathbb{R}}^n$，函数 $f$ 满足 $f(x)=J_{x}f\cdot x+{\sum }_i{J}_{b_i}f\cdot b_i$，则称函数 $f$ 是 FullGrad-complete（即FG-complete）。其中，$J_{x}f=\frac{\partial f}{\partial x}\in {\mathbb{R}}^{m\times n}$ 是 $f$ 关于 $x$ 的雅可比矩阵，代表 $f$ 对输入 $x$ 的各维度偏导数构成的矩阵；$J_{b_i}f=\frac{\partial f}{\partial b_i}\in {\mathbb{R}}^{m\times d_i}$ 是 $f$ 关于偏置项 $b_i$ 的雅可比矩阵 ，表示 $f$ 对不同偏置项的各维度偏导数构成的矩阵。
• 意义和作用：FG-完整性确保了模型输出在归因过程中，所有影响输出的因素都能被合理地分解到输入特征和偏置项的贡献中，使得归因的总和等于模型的输出，不存在未被解释的部分。这一属性对基于梯度的归因方法的忠实性至关重要，保证了在计算归因分数时，不会将无关影响错误地归因于输入，为准确理解模型决策过程提供了理论基础。在后续研究中，该定义用于判断经典神经网络架构和 Transformer 架构是否满足FG-完整性，进而分析基于梯度的归因方法在不同架构上的有效性。

经典架构的FG完备性-FG-Completeness of Classical Architectures

该部分主要证明了经典神经网络架构满足FG-完整性（FullGrad-Completeness），解释了基于梯度的归因方法在经典架构上有效的原因，具体内容如下：

1. 局部仿射函数的定义： 函数 $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 在点 $x_0\in {\mathbb{R}}^n$ 处是局部仿射的，当且仅当存在包含 $x_0$ 的开邻域 $U\subset {\mathbb{R}}^n$、矩阵 $W(x_0)\in {\mathbb{R}}^{m\times n}$ 和向量 $b(x_0)\in {\mathbb{R}}^m$，使得对于所有 $x\in U$，都有 $f(x)=W(x_0)x+b(x_0)$. 许多神经网络中使用的激活函数，如ReLU，是分段线性的，几乎处处局部仿射。
2. 局部仿射函数满足FG-完整性的定理： 任何在 $x_0$ 处局部仿射的函数在 $x_0$ 的邻域内是FG-完整的。证明过程是基于局部仿射函数在邻域内可表示为 $f(x)=W(x_0)x+b(x_0)$ 的形式，而这种形式属于仿射函数，根据已有的关于仿射函数FG-完整性的结论（后续定理6证明了任何仿射函数是FG-完整的 ），可得出该结论。
3. FG-完整性在函数组合和加法下的保持性
   • 函数组合：有限个FG-完整函数的组合仍然是FG-完整的。通过对两个FG-完整函数 $f_1$ 和 $f_2$ 的组合进行推导（利用链式法则等），证明了组合函数 $f=f_2\circ f_1$ 满足FG-完整性的定义，进而通过归纳法证明了有限个FG-完整函数组合的情况。
   • 函数加法：若 $f_1$ 和 $f_2$ 是FG-完整函数，则它们的和 $f=f_1+f_2$ 也是FG-完整的。根据 $f_1$ 和 $f_2$ 的FG-完整性表达式，推导出 $f$ 的雅可比矩阵与 $x$、偏置项乘积之和等于 $f(x)$，从而证明了该结论。
4. 经典神经网络架构的FG-完整性：经典神经网络采用多种仿射变换，如线性变换、卷积、池化、BatchNorm（评估模式）、LayerScale等，结合分段线性激活函数和跳跃连接，根据上述关于局部仿射函数、函数组合和加法的结论，可得出经典神经网络在 ${\mathbb{R}}^n$ 上是FG-完整的。这就解释了为什么基于梯度的归因方法在经典神经网络架构上能够有效应用。

Transformer中的非局部仿射层-Non-Locally-Affine Layers in Transformers

此部分指出，尽管经典架构具有FG-完整性，但现代 Transformer 模型引入的一些非局部仿射操作打破了这一特性，为后续分析梯度流不平衡及提出解决方案做了铺垫，具体内容如下：

1. 门控激活：像 GELU和 SiLU（Swish）这类函数，涉及非线性门控机制。这种非线性特性破坏了FG-完整性所要求的线性关系，进而影响了梯度流的正常传递。
2. 注意力机制：自注意力和交叉注意力层基于非线性的注意力分数进行加权平均。这种操作打破了线性性质，使得在计算归因时无法满足FG-完整性，导致梯度流出现不平衡的情况。
3. 乘法特征融合：例如 SwiGLU、MambaOut 等操作，涉及不同前馈分支的逐元素乘法。这种乘法运算打破了FG-完整性所需的线性条件，对梯度流产生干扰，最终影响归因的准确性。
4. 归一化：LayerNorm 操作通过除以标准差来实现归一化，其中的除法运算属于非线性操作。这一操作破坏了线性关系，使得 FullGrad 在处理相关计算时出现问题，例如当 $\epsilon$ 趋近于 0 时，FullGrad 在 LayerNorm 操作上的结果趋近于零，从而破坏了FG-完整性，引发梯度流不平衡。

梯度流不平衡分析-Analysis of Gradient Flow Imbalance

该部分聚焦于 Transformer 中梯度流不平衡的问题，从理论层面分析了非局部仿射操作对梯度流的具体影响，为后续提出的解决方法做了理论铺垫，具体内容如下：

1. 逐元素乘法对FG-完整性的影响：对于两个FG-完整函数 $f_1$ 和 $f_2$，其逐元素乘积 $f(x)=f_1(x)\odot f_2(x)$ 通常不满足FG-完整性。从其雅可比矩阵计算可得 $J_{x}f\cdot x+{\sum }_i{J}_{b_i}f\cdot b_i=2f(x)$，而不是等于 $f(x)$，这表明逐元素乘积操作会使FG-完整性等式的结果变为期望输出的两倍，从而破坏了FG-完整性。进一步分析可知，当两个路径在相乘前并非都满足FG-完整性时，乘法运算往往会加剧已有的梯度流不平衡，而非恢复FG-完整性 。
2. 除法操作对梯度流的影响：当 $f_1$ 和 $f_2$ 是FG-完整函数且 $f_2$ 非零时，对于它们的逐元素商 $f(x)=f_1(x)\oslash f_2(x)$，FullGrad 的结果会完全消失为零。以 LayerNorm 操作为例，其在计算过程中涉及除法运算，即使不满足命题2中对分子分母都为FG-完整的条件要求，但在实际情况中，当 $\epsilon$ 趋近于0时，FullGrad 在 LayerNorm 操作上的结果 $li{m}_{\epsilon \to 0}{J}_{x}LN\cdot x=0$，这表明 LayerNorm 操作会导致梯度流出现问题，使得基于梯度的归因在该操作上失效。

LibraGrad: 理论基础-LibraGrad: Theoretical Foundations

该部分主要介绍了 LibraGrad 的理论基础，旨在解决 Transformer 中梯度流不平衡的问题，具体内容如下：

1. 实现FG-完整性的条件：对于两个FG-完整函数 $f_1$ 和 $f_2$，当它们的逐元素乘积 $f(x)=f_1(x)\odot f_2(x)$ 的雅可比矩阵使用满足 $a+b=1$ 的缩放系数 $a$ 和 $b$ 进行定义时，即 $J_{x}f=a[diag(f_2(x))\cdot J_x{f}_1]+b[diag(f_1(x))\cdot J_x{f}_2]$，$J_{b_i}f=a[diag(f_2(x))\cdot J_{b_i}{f}_1]+b[diag(f_1(x))\cdot J_{b_i}{f}_2]$，函数 $f$ 是FG-完整的。这表明通过合理缩放雅可比矩阵，可以使逐元素乘积操作满足FG-完整性，为解决梯度流不平衡问题提供了理论依据。
2. 特殊情况下的FG-完整性：当 $a=0$ 时，$f(x)=[f_1(x){]}_{cst.}\odot f_2(x)$（其中 $[\cdot {]}_{cst.}$ 是使梯度为零的常数算子），若 $f_2$ 是FG-完整的，则 $f$ 也是FG-完整的；同理，当 $b=0$ 时，若 $f_1$ 是FG-完整的，$f$ 也为FG-完整。这进一步说明了在不同条件下，如何通过调整梯度计算方式来保证函数的FG-完整性。
3. 解决除法操作的梯度问题：对于除法操作，可将其视为与梯度修剪后的非线性倒数的逐元素乘法，即 $f(x)=f_1(x)\odot [1/f_2(x){]}_{cst}$，根据上述理论，这样的处理方式能使除法操作满足FG-完整性。以 LayerNorm 操作为例，在反向传播时将分母视为常数，能够恢复适当的梯度流，解决了 LayerNorm 操作导致梯度流异常的问题。
4. 提出通用原则和操作算子：基于上述理论结果，提出通过对反向路径进行战略剪枝和缩放可以实现平衡梯度流，且无需修改前向计算。为此定义了两个梯度操纵算子：
   • 常数算子：常数算子 $[\cdot {]}_{cst.}:{\mathbb{R}}^m\to {\mathbb{R}}^m$，满足 $[y{]}_{cst.}=y$，$J_x[y{]}_{cst.}=0$，它可以通过将梯度设置为零来实现对特定路径的剪枝。
   • SwapBackward算子：SwapBackward $(f,g)\mapsto h$ 算子，其中 $f,g,h:{\mathbb{R}}^n\to {\mathbb{R}}^m$，定义为 $h(x)=f(x)$，$J_{x}h=J_{x}g$。该算子可以在保持函数值不变的情况下，改变梯度的传播方式。这两个算子为实现 LibraGrad 的梯度调整提供了具体的操作手段，且它们的计算复杂度与标准梯度相比并未增加 。

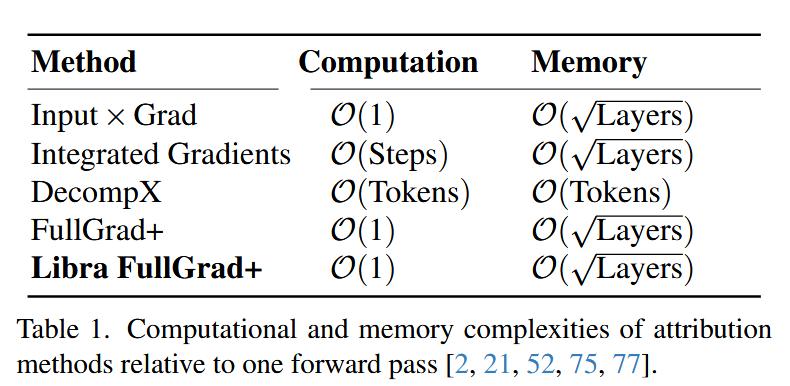
LibraGrad: 实际应用-LibraGrad: Practical Implementation

该部分介绍了 LibraGrad 在实际中的实现方式，针对 Transformer 中的常见非仿射操作提出了对应的FG-完整版本，为在 Transformer 架构中应用 LibraGrad 提供了实践指导，具体内容如下：

1. Libra Attention：在注意力机制中，通过限制梯度仅在值分支传播，使得该操作变为局部仿射，进而满足FG-完整性。具体实现为 $Libra-Attention(Q,K,V)=[softmax\left(Q{K}^T\right){]}_{cst.}\cdot V$，其中 $[softmax\left(Q{K}^T\right){]}_{cst.}$ 利用常数算子将 $softmax\left(Q{K}^T\right)$ 的梯度置零，仅保留值分支 $V$ 的梯度传播，从而实现局部仿射和FG-完整性。
2. Libra Gated Activation：对于如 GELU 和 SiLU 这类门控激活函数，通过丢弃非线性门的梯度来实现。即 $Libra-GatedActivation(x)=x\odot [NonLinearGate(x){]}_{cst.}$ ，使用常数算子将非线性门的梯度设为零，避免其对梯度流的不良影响，保证了整体操作的FG-完整性。
3. Libra Self-Gating：在自门控操作（如SwiGLU）中，输入经过双平行前馈路径后通过逐元素乘法重新合并。为平衡分支间的梯度流，对每个分支的梯度进行缩放。具体实现为 $Libra-SelfGate(x)=SwapBackward\left(f_1\odot f_2,\frac{1}{2}\left(f_1\odot f_2\right)\right)(x)$，利用 SwapBackward 算子，将 $f_1\odot f_2$ 的梯度替换为 $\frac{1}{2}\left(f_1\odot f_2\right)$ 的梯度，实现了对梯度的缩放，平衡了梯度流。
4. Libra LayerNorm：根据前文理论，将 LayerNorm 操作中的分母视为常数处理来恢复合适的梯度流。具体表达式为 $Libra-LayerNorm(x)=\frac{x-\mu }{{\left[\sqrt{{\sigma }^2+\epsilon }\right]}_{cst.}}$，通过对分母应用常数算子，解决了 LayerNorm 操作中由于除法导致的梯度流问题，使其满足FG-完整性。
5. 整体效果：当 Transformer 架构中的所有非线性组件（包括注意力机制、激活函数、自门控操作和LayerNorms）都被替换为相应的 Libra 版本时，整个 Transformer 架构能够实现 FG-完整性。从实际效果来看，LibraGrad 的梯度平衡机制不仅能使模型满足理论上的 FG-完整性，还在经验上普遍增强了基于梯度的归因方法的性能。这是因为标准梯度流存在过度强调局部敏感模块，以及在像 LayerNorm 这样的操作中给分母分配反作用负信号等问题，而 LibraGrad 有效改善了这些问题 。

---

实验-Experiments

实验设置-Experimental Setup

该部分主要介绍了实验的具体设置，包括所选用的模型、数据集以及评估指标等，为后续实验结果的准确性和可靠性提供了基础，具体内容如下：

1. 模型选择：评估涵盖了八个模型家族，分别为ViT、EVA2、BEiT2、FlexiViT、SigLIP、CLIP、DeiT3、MLPMixer。实验使用了这些模型在ImageNet-1k上微调的最大变体（其中EVA2因硬件限制选择了EVA2-S ）。对于ViT模型，还额外测试了tiny、small、base和large等不同尺寸，以探究LibraGrad在不同规模模型上的效果。
2. 数据集选择
   • ImageNet：作为标准的基准数据集，在归因文献中被广泛使用，用于评估各种模型和方法。
   • ImageNet-Hard：该数据集具有挑战性，它结合了多个现有ImageNet变体，如ImageNet-V2、ImageNet-Sketch、ImageNet-C等。实验从该数据集中随机选择1000张图像进行测试。
   • MURA和Oxford-IIIT Pet：MURA是一个医学X射线数据集，Oxford-IIIT Pet是宠物图像数据集。在ViT-B模型上，也使用这两个数据集进行实验，同样各随机选择1000张图像 。
3. 评估指标
   • Faithfulness Metrics（忠诚度指标）：通过测量在逐步遮挡输入特征时模型行为的变化，来量化归因分数反映输入特征对模型预测重要性的准确程度。常用的忠诚度指标包括Most-Influential-First Deletion（MIF）、Least-Influential-First Deletion（LIF）和Symmetric Relevance Gain（SRG）。本文主要报告了MIF指标，通过跟踪按归因重要性递减顺序遮挡特征时模型的性能下降情况（使用预测标签和准确率测量）来评估。详细的指标计算方法和所有相关指标结果在附录B.2和附录D中给出。
   • Completeness Error（完整性误差）：用于验证理论保证和实现的正确性。通过计算 $CE(f,x,A)=\Vert f(x)-{\sum }_{i=1}^{n}A(f)(x{)}_i\Vert$ 来衡量，较低的CE值表示模型输出在归因分数中保留得更好。实验仅使用ImageNet数据集中的100张随机图像进行该指标的测试，具体细节在附录B.1中给出。
   • Segmentation（分割）：选择ImageNet-S数据集进行评估，该数据集包含919个不同的类。实验使用其验证集中的5000张随机图像，利用分割掩码提供的真实对象边界注释，客观地评估特征归因方法识别对模型预测真正相关图像区域的能力，具体细节在附录B.3中给出。

定量结果-Quantitative Results

该部分呈现了 LibraGrad 方法在多个模型、数据集上的定量实验结果，从多个维度评估了 LibraGrad 对不同梯度归因方法的提升效果，有力地证明了其有效性和优越性，具体内容如下：

1. 整体提升效果：LibraGrad 在所有测试的模型、架构和数据集上，普遍增强了基于梯度的归因方法的性能。在 Faithfulness 和 Segmentation 指标上均有显著改进，Libra FullGrad 在 Completeness Error 指标上达到最优，这些提升效果在不同模型规模和数据集上保持一致，并且在无注意力机制的 MLP-Mixer 模型上也得到验证，表明梯度流不平衡是导致现有方法效果不佳的核心问题，而非注意力机制本身。
   
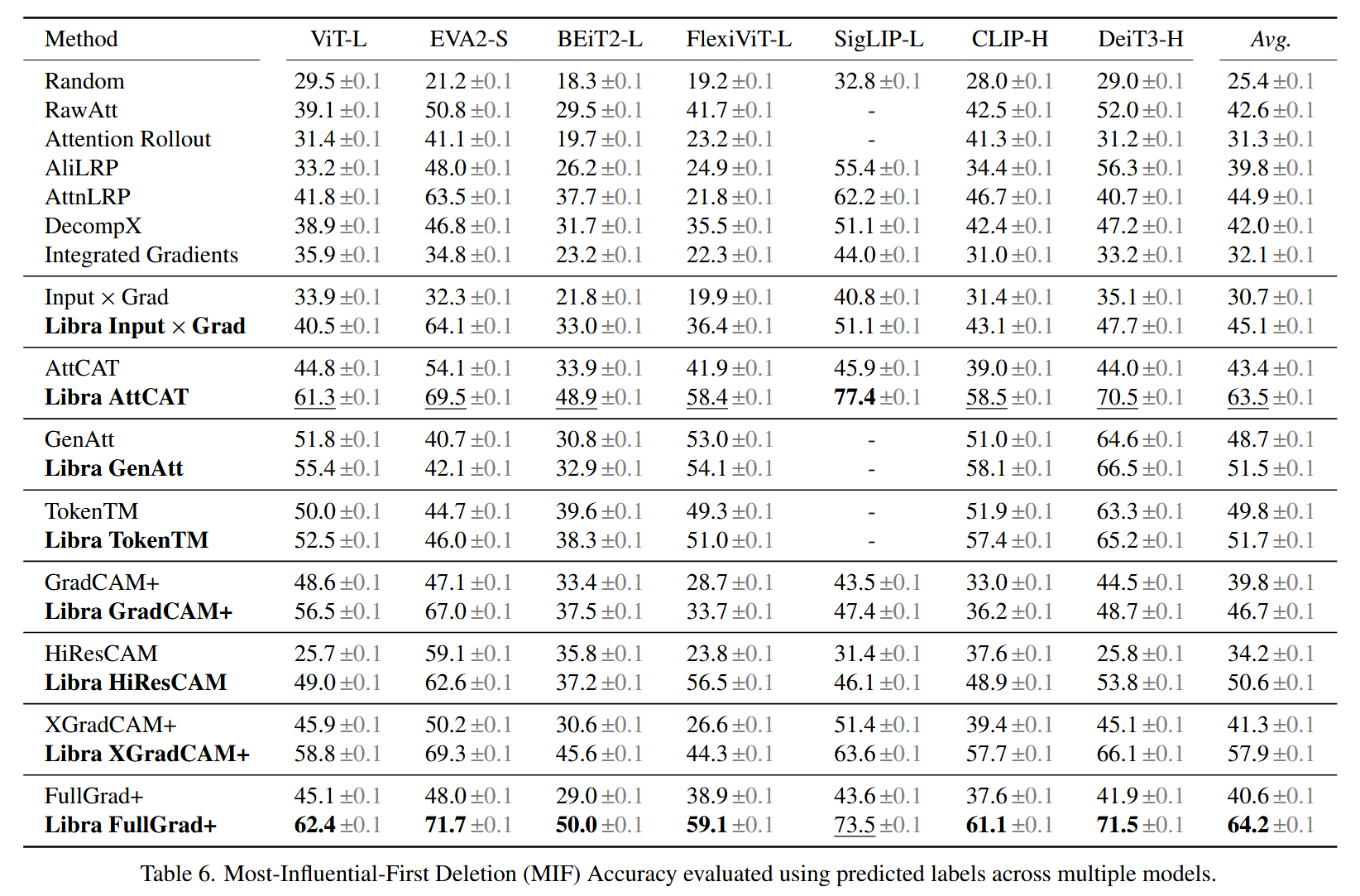
   表6. 跨多个模型使用预测标签评估的最具影响力优先删除（MIF）准确率。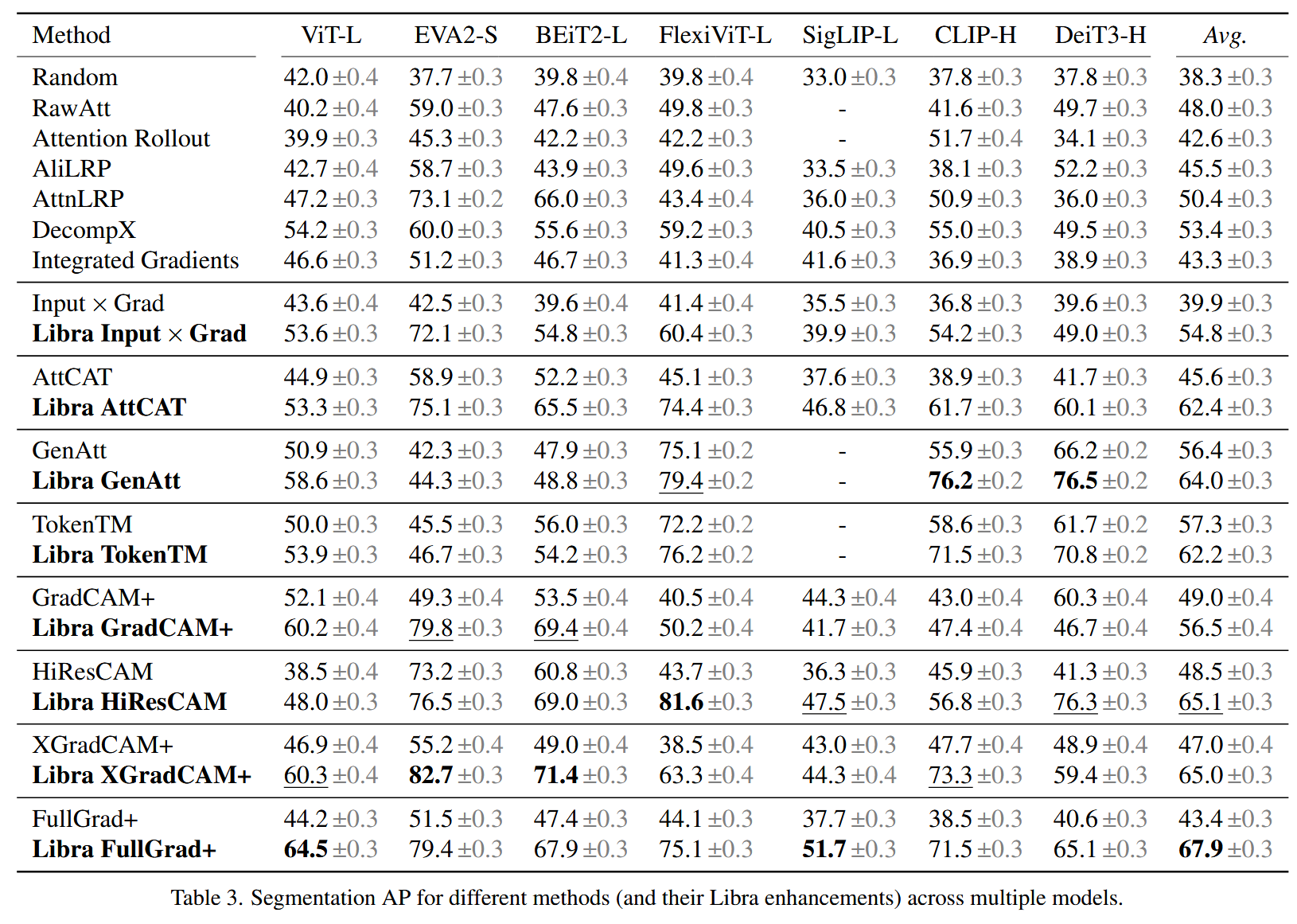
   
   表3. 跨多个模型的不同方法（及其基于Libra的改进版本）的分割平均精度（AP）。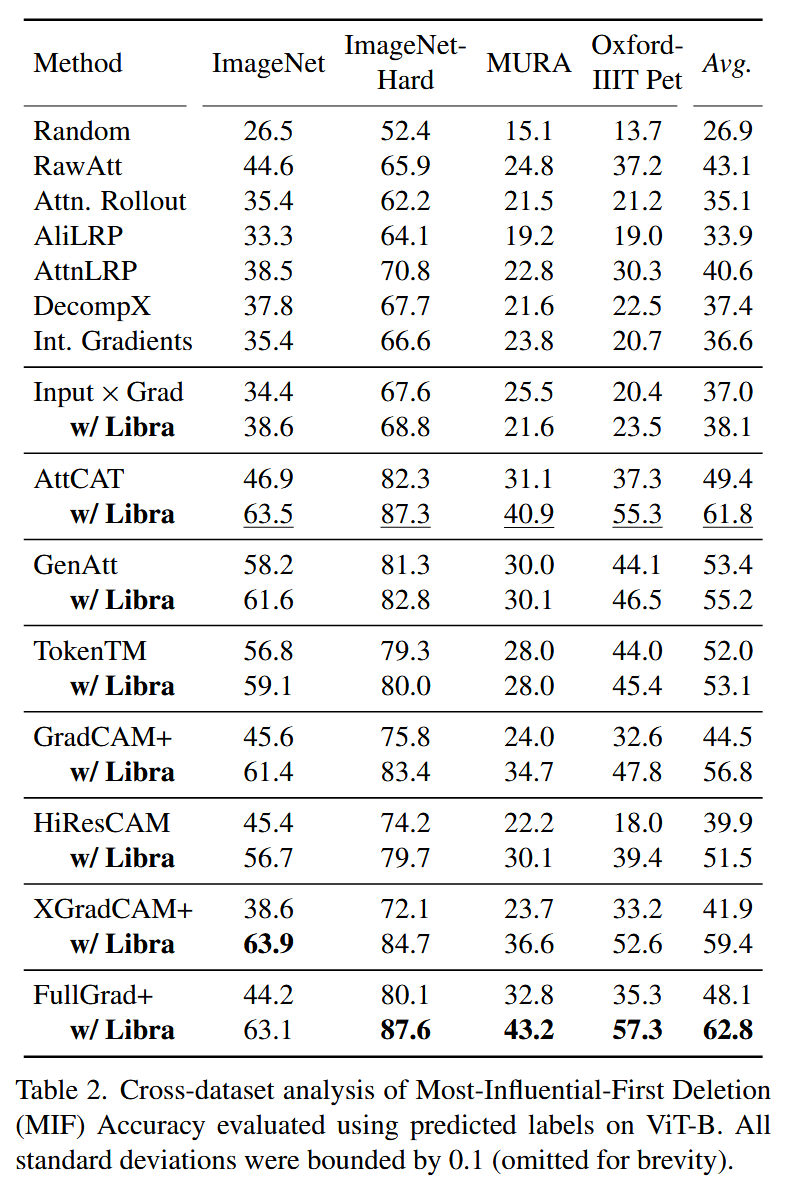
   
   表2. 在ViT-B模型上使用预测标签对最具影响力优先删除（MIF）准确率进行的跨数据集分析。所有标准差均在0.1以内（为简洁起见省略）。
2. 与集成梯度方法的对比：将LibraGrad与集成梯度（IG）方法进行比较，发现LibraGrad在提升现有方法性能方面远优于IG。由于IG在实际应用中存在数值不稳定性，其基于固定步长近似的实践结果无法达到理论上相对于零基线的完整性承诺（如在Completeness Error指标上表现不佳），并且从理论上证明了这种数值不稳定性在固定步长近似下是不可避免的。
   
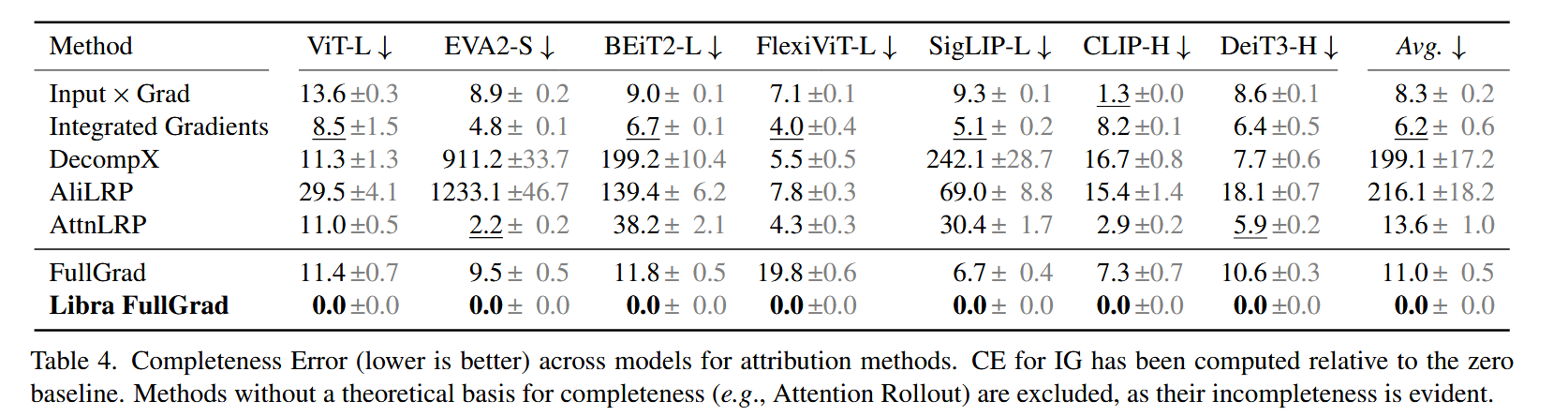
   表4. 不同归因方法在多个模型上的完整性误差（越低越好）。集成梯度（IG）的完整性误差是相对于零基线计算的。由于像注意力传播（Attention Rollout）这类方法明显不具备完整性，且缺乏完整性的理论基础，因此未被纳入该表。
3. 通用方法的优势：在梯度流得到纠正后，通用的 FullGrad+ 方法在大多数指标和模型上，性能优于专为 Transformer 设计的方法（如 GenAtt、TokenTM 和 AttCAT ），在少数情况下也能保持竞争力。这表明在梯度流平衡的情况下，专门为特定架构设计的归因方法可能并非必要。
4. 消融研究结果：通过消融研究得到三个关键发现：一是虽然理论上某些门控激活函数会破坏FG - 完整性，但在实际中其影响较小，因为它们通常在饱和状态下运行；二是LayerNorm操作中理论预测的归因消失问题在实验中得到证实，是影响归因效果的最显著因素；三是虽然偏置项对理论完整性有必要，但在实际应用中其影响较小，在实现过程中可选择省略而不会带来严重后果。
   
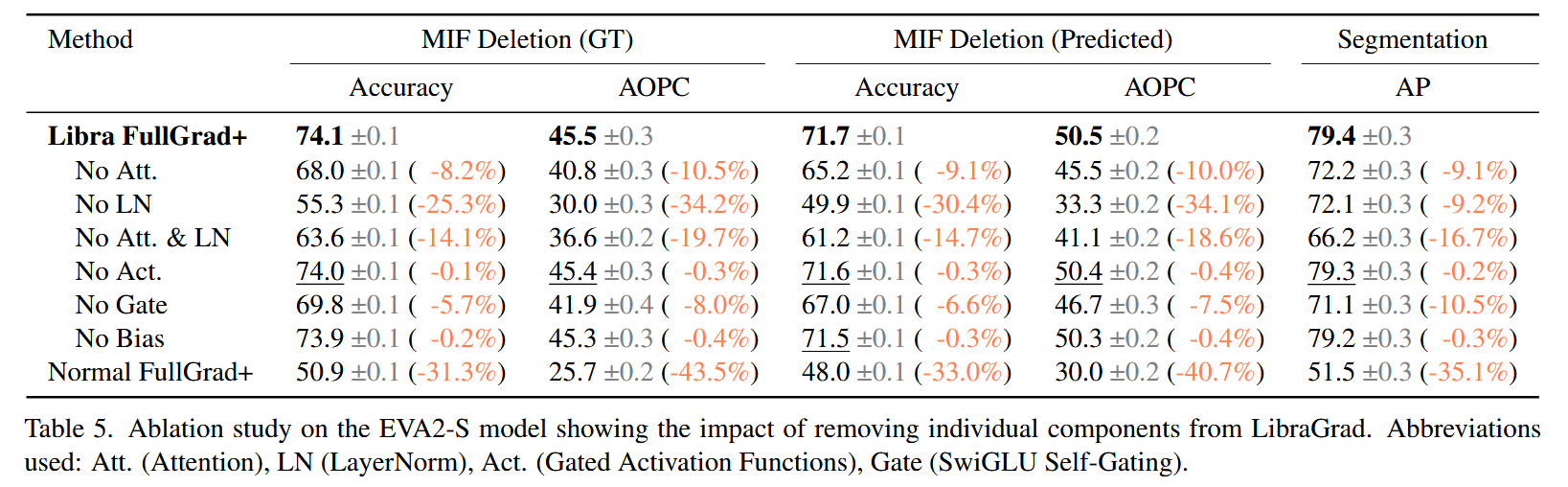
   表5. 对 EVA2-S 模型进行的消融研究，展示了从 LibraGrad 中去除单个组件的影响。所使用的缩写：Att.（注意力机制）、LN（层归一化）、Act.（门控激活函数）、Gate（SwiGLU自门控）。

定性分析-Qualitative Analysis

该部分通过两个互补场景对Libra FullGrad+进行定性分析，进一步验证了LibraGrad在提升模型归因质量方面的有效性，具体内容如下：

1. 文本提示区域归因（使用CLIP模型）：利用CLIP模型能输出图像-文本对相似性分数的特性，以该分数作为归因目标。针对每个测试图像，通过系统地使用不同的文本提示探测不同区域和概念，来详细评估各归因方法在复杂场景中定位描述元素的能力。实验结果表明，Libra FullGrad+能够生成精确的提示特定归因图，相比现有方法，在解释“勺子和叉子”等提示的模型输出时，定位效果得到明显提升，证明了其在复杂场景下精确定位相关元素的能力。
2. 多类判别（使用ImageNet微调模型）：选用 ImageNet 微调模型，对精心挑选的COCO 2017训练集中同时包含斑马和大象且二者都清晰可见、未被显著遮挡的图像进行评估。将“斑马”和“非洲象”的输出类概率作为归因目标，这是因为先前研究表明这两种动物是评估归因的有效测试案例，且它们在ImageNet中的类别设置以及自然共现和独特视觉特征有助于验证归因的类别特异性。实验结果显示，Libra FullGrad+在该场景下能够准确区分共现的动物类别，再次验证了定量研究中发现的适当梯度流可使通用方法优于专门方法的结论。

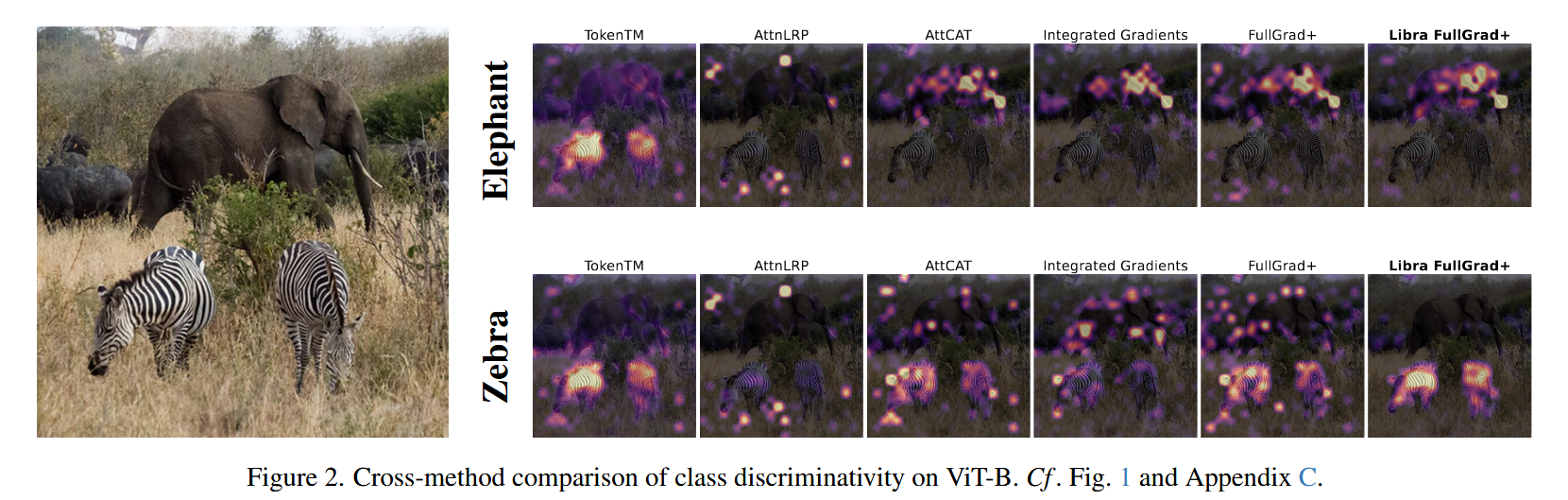
图2. 在ViT-B模型上不同方法的类别判别能力比较。参考图1和附录C。

---

结论-Conclusion

论文在结论部分总结了 LibraGrad 方法的核心成果、理论贡献、实践意义，并对未来研究方向做出展望，具体内容如下：

1. LibraGrad 方法的有效性：提出 LibraGrad 方法，该方法通过对反向路径进行剪枝和缩放，有效纠正了 Transformer 中的梯度流不平衡问题。
2. 理论贡献：正式定义了FG-完整性概念，证明经典 CNNs 天然具有FG-完整性，这解释了基于梯度的方法在经典 CNNs 上成功的原因。同时指出，现代 Transformer 中的部分操作打破了这一属性，而 LibraGrad 为恢复 FG-完整性提供了理论证明和实际解决方案，且无需修改前向传递过程。
3. 实践意义：大量实验表明，LibraGrad 能在不同架构、模型尺寸和数据集上，普遍增强基于梯度的归因方法的性能。使得通用方法（如FullGrad+）在梯度流平衡时，性能超越专为 Transformer 设计的方法。定性分析结果进一步验证了这一优势，表明在处理复杂场景和多类别判别时，LibraGrad 能使模型表现更优。
4. 未来研究方向：未来工作可探索LibraGrad与其他基于梯度的方法的组合应用，研究其作为梯度正则化器的潜力，以及将其扩展到新兴架构创新中的可行性，为进一步提升模型可解释性和性能提供更多可能。