文章对比了稠密模型中的增强版FFN和稀疏模型MoE的结构与原理。增强版FFN引入门控机制提高表达能力；MoE通过选择top-k专家实现计算效率与模型容量平衡。详细介绍了MoE工作原理、训练与推理阶段的差异，以及通过辅助损失解决负载均衡问题的方法，这些技术是现代大语言模型提高效率的重要手段。

---

一、稠密模型中的FFN

稠密模型（Dense Model）是指模型结构中所有的参数和计算路径在每次前向计算中都会被激活，与下一小节要介绍的稀疏模型MoE形成对比。

相比于原始Transformer中使用的FFN，这里的FFN引入了Gated结构，可以动态地控制信息流通（比如抑制/强调特定特征），增加了表达能力。目前很多SOTA模型（如 LLaMA、PaLM、GPT-NeoX、ChatGLM）都不再用原始 FFN，而是使用带门控机制（Gated）的前馈神经网络FFN。

这里对两者进行对比：

特性	标准 FFN	增强版 FFN（Gated）
激活函数	ReLU / GELU	GELU / SiLU / Swish 等
中间结构	单路计算	双路计算（乘积）
参数量	较少	多一个 Linear 层
非线性能力	一般	更强（引入乘法门控）
性能表现	基线	表现更好（SOTA 标配）

增强版FFN的代码实现如下：

# 激活函数映射字典ACT2FN = {    "relu": F.relu,    "gelu": F.gelu,    "silu": F.silu}class FeedForward(nn.Module):    def __init__(self, config: dict):        super().__init__()        if config["intermediate_size"] isNone:            intermediate_size = int(config["hidden_size"] * 8 / 3)            # 为了更好地利用 GPU 的并行计算能力（特别是 TensorCore、SIMD 等），中间维度通常会做 64 对齐            # 向上取整到最近的 64 的倍数            config["intermediate_size"] = 64 * ((intermediate_size + 64 - 1) // 64)        self.gate_proj = nn.Linear(config["hidden_size"], config["intermediate_size"], bias=False)        self.down_proj = nn.Linear(config["intermediate_size"], config["hidden_size"], bias=False)        self.up_proj = nn.Linear(config["hidden_size"], config["intermediate_size"], bias=False)        self.dropout = nn.Dropout(config["dropout"])        self.act_fn = ACT2FN[config["hidden_act"]]    def forward(self, x):        return self.dropout(            self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))        )# 示例配置config = {    "hidden_size": 512,    "intermediate_size": None,  # 自动计算    "dropout": 0.1,    "hidden_act": "silu"# 也可以试试 "gelu", "relu"}# 创建模型和输入ffn = FeedForward(config)x = torch.randn(2, 16, 512)  # (batch_size, seq_len, hidden_size)# 前向传播out = ffn(x)print("Output shape:", out.shape) # Output shape: torch.Size([2, 16, 512])

这里的“门控机制”具体的逻辑是这样的：

首先，通过 gate = act_fn(gate_proj(x)) 得到门控信号（范围通常为[0, 1]或正数）；

其次，通过 value = up_proj(x) 得到要被控制的信息通道；

接着，使用 gated = gate * value 应用门控，控制信息强度（本质上就是加权）；

最后，使用output = down_proj(gated) 降维回去，门控完成。

二、稀疏模型MoE

2.1 MOE的工作原理

稠密模型适合中小规模模型结构，部署和训练更简单稳定，是大多数基础模型（如GPT、BERT、LLaMA）的核心形式。

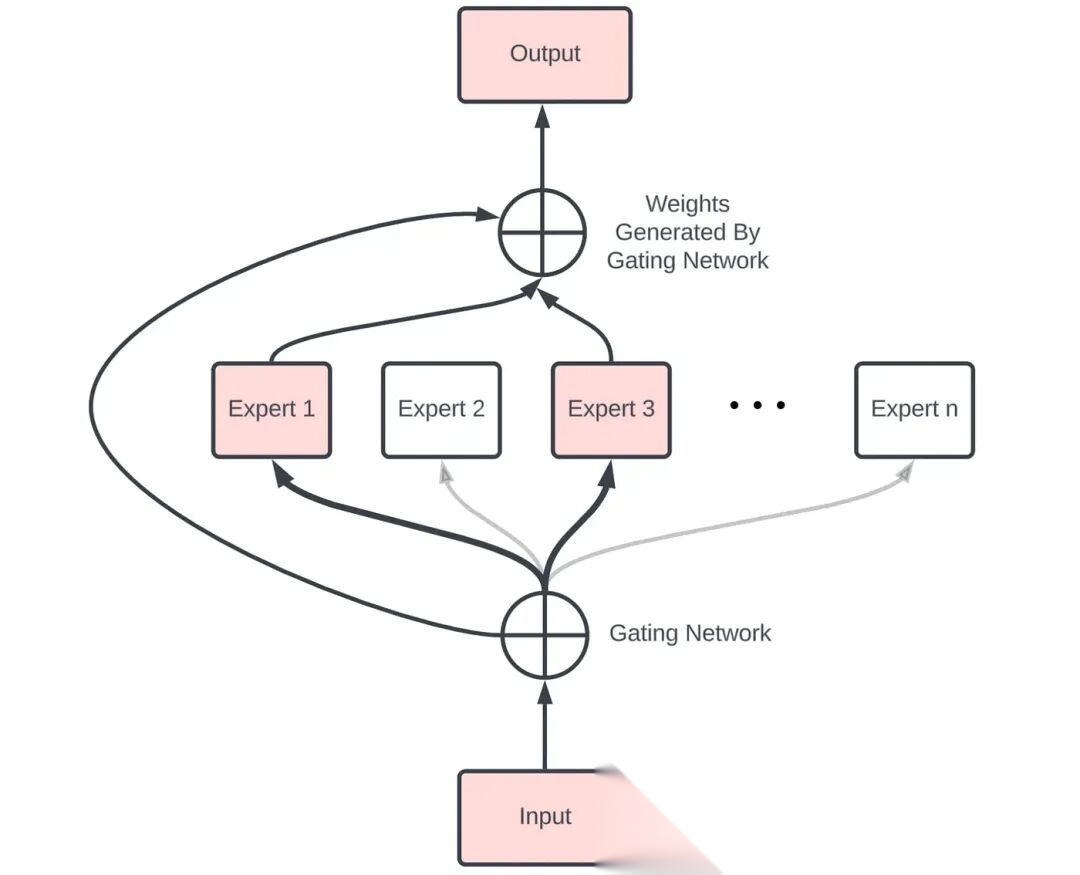
但如果想让模型变得更大、更强，而又不想付出巨额推理开销，可以使用稀疏模型（比如MoE），这是一种更具扩展性的结构。其核心思想是：模型参数很多，但每次只激活其中一部分（部分专家），通过门控（Gating）机制选择专家进行预测、最后组合专家输出。

参考：

https://medium.com/@drahyhenc/mixture-of-experts%E5%AD%B8%E7%BF%92%E7%AD%86%E8%A8%98-80fae09a1b5e

在MiniMind中，MOE主要应用在Attention之后的FFN上。

原始的FFN使用的是我们上面定义的一个FeedForward类，而MOE的思想是将“原始FFN中只包含一个FeedForward”替换成“FFN中包含多个FeedForward”，其中每一个FeedForward都是一个专家，这乍看上去增加了很多参数，但是在实际的数据流动时，只会选择其中top-k个专家，也就是只会激活top-k个FeedForward，从而节省计算时间（但是还是需要将所有专家都加载到显存的，不省显存省时间，应对策略是把模型放在主内存里，需要的时候把相应的专家模型加载到显卡上进行推理）。

注意，在训练时，每一个专家都会被更新参数，训练完成后，“不同的专家擅长不同领域知识”这一目标就达成了，每个专家都得到了训练。在数据流向MOE时，会根据“学习到的经验”选择合适的专家进行处理。

现将MOE的执行流程总结为如下四步：

第一步、对每个 token，使用 MoEGate 打分，选择 top-k 个专家（例如 k=2）

第二步、只将 token 输入给这 k 个专家（repeat_interleave）

第三步、每个专家输出后加权求和（使用 gate 输出的 softmax 权重）

第四步、返回合并后的输出

相应的MOE主体实现代码如下：

class MOEFeedForward(nn.Module):    def __init__(self, config):        super().__init__()        self.config = config        # 初始化专家网络（仅路由专家）        self.experts = nn.ModuleList([            FeedForward(config)            for _ in range(config.n_routed_experts)        ])        # 初始化门控网络        self.gate = MoEGate(config) # MoEGate 将在下一小节介绍        # 可选：共享专家网络（作用于每个 token）        if config.n_shared_experts > 0:            self.shared_experts = nn.ModuleList([                FeedForward(config)                for _ in range(config.n_shared_experts)            ])    def forward(self, x):        """        x: [bsz, seq_len, hidden_size]        """        identity = x  # 用于 residual 加上共享专家输出        orig_shape = x.shape        bsz, seq_len, _ = x.shape  # bsz = batch size, seq_len = token 数量        # ===== 1. 门控阶段：选择 top-k 个专家 作为每个 token 的路由 =====        topk_idx, topk_weight, aux_loss = self.gate(x)        # topk_idx:    [bsz * seq_len, top_k]        # topk_weight: [bsz * seq_len, top_k]        # ===== 2. Flatten token 维度，准备并行处理 token =====        x = x.view(-1, x.shape[-1])        # x: [bsz * seq_len, hidden_size]        flat_topk_idx = topk_idx.view(-1)        # flat_topk_idx: [(bsz * seq_len) * top_k]，表示每个 token 被分配到的专家 ID        if self.training:            # ===== 3. 训练阶段：每个 token 被复制 top_k 次，送入不同专家 =====            x = x.repeat_interleave(self.config.num_experts_per_tok, dim=0)            # x: [(bsz * seq_len) * top_k, hidden_size]            # 用于收集每个专家处理后的结果            y = torch.empty_like(x, dtype=torch.float16)            # 遍历每个专家，将其处理分配给它的 token            for i, expert in enumerate(self.experts):                # 找出所有分配给第 i 个专家的 token                mask = (flat_topk_idx == i)                x_i = x[mask]  # [num_token_i, hidden_size]                if x_i.shape[0] > 0:                    y[mask] = expert(x_i).to(y.dtype)  # expert 输出: [num_token_i, hidden_size]            # 恢复 top_k 维度，并根据 gate 分数加权平均            y = y.view(*topk_weight.shape, -1)  # [bsz * seq_len, top_k, hidden_size]            y = (y * topk_weight.unsqueeze(-1)).sum(dim=1)# 在 top_k 维度进行了加权求和            # y: [bsz * seq_len, hidden_size]            # reshape 回原始形状            y = y.view(*orig_shape)  # [bsz, seq_len, hidden_size]        else:            # ===== 4. 推理阶段：使用高效推理模式（按专家分组处理） =====            topk_weight = topk_weight.view(-1, 1) # [bsz * seq_len, top_k] --> [bsz * seq_len * top_k, 1]            y = self.moe_infer(x, flat_topk_idx, topk_weight)            y = y.view(*orig_shape)  # [bsz, seq_len, hidden_size]        # ===== 5. 加上共享专家的输出（可选）=====        if self.config.n_shared_experts > 0:            for expert in self.shared_experts:                y = y + expert(identity)  # 每个共享专家都作用在原始输入上并加到输出上        self.aux_loss = aux_loss  # 保存门控产生的辅助损失        return y        @torch.no_grad()    def moe_infer(self, x, flat_expert_indices, flat_expert_weights):        """        推理阶段的 MoE 前向传播。按照专家编号将 token 分组，分别送入对应专家中计算后合并。                参数：        - x: [bsz * seq_len, hidden_size]             所有 token 的表示（没有复制）        - flat_expert_indices: [(bsz * seq_len) * top_k]  每个 token 被路由到的专家编号        - flat_expert_weights: [(bsz * seq_len) * top_k , 1] 每个专家对应的门控权重        """        # 初始化输出缓存，与 x 同 shape 和 dtype        expert_cache = torch.zeros_like(x)  # shape: [bsz * seq_len, hidden_size]        # 1. 根据专家编号对所有 token 排序（为了把分配到相同专家的 token 放到一起）        idxs = flat_expert_indices.argsort()  # 按照专家索引从小到大排序后得到 专家分组排序后token（复制了top_k倍）的索引， 这是一个列表        # 2. 统计每个专家分配到的 token 数量并累加，方便切分        tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)        # tokens_per_expert[i] 表示第 i 个专家前面（由其它专家）累积处理了多少个 token        # 3. 计算按照专家分组排序后的 token 属于哪些原始 token（因为每个 token 会被复制 top_k 次）        token_idxs = idxs // self.config.num_experts_per_tok        # shape: [(bsz * seq_len) * top_k]        # 4. 遍历每个专家，将分配到该专家的 token 送入对应 FFN 计算            # 当tokens_per_expert = [6, 15, 20, 26]，tokens_per_expert.shape[0]即为专家数量（此时为4）            # 且token_idxs = [3, 7, 19, 21, 24, 25,  4,  5,  6, 10, 11, 12...] 时            # 意味token_idxs[:6] -> [3, 7, 19, 21, 24, 25]这6个位置属于专家0处理的token（每个token有可能被多个专家处理，这取决于num_experts_per_tok）            # 接下来9个位置token_idxs[6:15] -> [4,  5,  6, 10, 11, 12...]属于专家1处理的token...依此类推        for i, end_idx in enumerate(tokens_per_expert):            start_idx = 0if i == 0else tokens_per_expert[i - 1]            if start_idx == end_idx:                continue# 该专家没有被分配 token            # 上述 start_idx ~ end_idx 是某一个专家i需要负责处理的token数量            expert = self.experts[i]  # 获取专家 FFN 模块            # 5. 获取分配给第 i 个专家的 token 原始位置索引            # 即：expert_out 中每一行对应的是原始输入中哪个 token。            exp_token_idx = token_idxs[start_idx:end_idx]  # [num_token_i]            # 6. 取出对应 token 表示            expert_tokens = x[exp_token_idx]  # [num_token_i, hidden_size]            # 7. 执行当前专家对应 FFN 的前向传播            expert_out = expert(expert_tokens).to(expert_cache.dtype)  # [num_token_i, hidden_size]            # 8. 用 gate 权重缩放输出            # expert_out.mul_(...)  等价于 expert_out = expert_out * ...            # [num_token_i, hidden_size] * [num_token_i, 1] --> [num_token_i, hidden_size]            expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])  # 权重 shape: [num_token_i, 1]            # 9. 累加到输出缓存中，支持一个 token 被多个专家处理后结果叠加            expert_cache.scatter_add_(                dim=0,                # [num_token_i] -->  [num_token_i, 1] --> [num_token_i, hidden_size]                index=exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]),                 # [num_token_i, hidden_size]                src=expert_out             )        # 最终输出 shape: [bsz * seq_len, hidden_size]        return expert_cache

在上述代码中，MiniMind实现的MOE代码中还加入了共享的专家，这些专家都作用在原始输入上并加到输出上。

同时，针对推理场景，上述代码实现了高效地将 token 分派给不同专家并进行前向计算、加权输出、聚合结果等操作。其核心思想是：按照专家(0, 1, 2, …)对复制top_k倍的所有token索引进行分组排序。

为了便于理解推理过程，这里举一个具体的例子。

假设我们有以下配置：

假设有以下配置：

bsz = 2             # batch sizeseq_len = 2         # 每个样本 2 个 tokenhidden_size = 4     # 每个 token 的向量维度top_k = 2           # 每个 token 路由到 top_k 个专家num_experts = 3     # 总共 3 个专家

也就是说：

• 总 token 数 = bsz * seq_len = 4
• 每个 token 分给 2 个专家，共 8 个分配记录
• x.shape = [4, 4]（4 个 token，每个是 4 维）

第一步、准备输入数据：

x = torch.tensor([    [0.1, 0.2, 0.3, 0.4],  # token 0    [1.0, 1.1, 1.2, 1.3],  # token 1    [2.0, 2.1, 2.2, 2.3],  # token 2    [3.0, 3.1, 3.2, 3.3],  # token 3])  # shape: [4, 4]

第二步、top-k 专家分配（假设已经由 gate 模块得出）：

flat_expert_indices = torch.tensor([    0, 1,   # token 0 → expert 0, 1    1, 2,   # token 1 → expert 1, 2    0, 2,   # token 2 → expert 0, 2    0, 1    # token 3 → expert 0, 1])  # shape: [8]# flat_expert_indices的含义是：# 第0个token被分配给专家0（flat_expert_indices[0]）# 第0个token被分配给专家1（flat_expert_indices[1]）# 第1个token被分配给专家1（flat_expert_indices[2]）# 第1个token被分配给专家2（flat_expert_indices[3]）# 第2个token被分配给专家0（flat_expert_indices[4]）# 第2个token被分配给专家2（flat_expert_indices[5]）# 第3个token被分配给专家0（flat_expert_indices[6]）# 第3个token被分配给专家1（flat_expert_indices[7]）# 也就是说，共有 4 个 token，每个 token 被复制分配了 2 次 → 长度 8。flat_expert_weights = torch.tensor([    [0.9], [0.1],   # token 0    [0.3], [0.7],   # token 1    [0.4], [0.6],   # token 2    [0.5], [0.5],   # token 3])  # shape: [8, 1]# flat_expert_weights 是对应的权重

第三步、推理阶段关键逻辑：

• Step 1: idxs = flat_expert_indices.argsort()

flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]idxs = flat_expert_indices.argsort()# 即：让所有 token 的分配记录按专家编号排好序# flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]# 对应排序后：# expert 0 负责: index 0, 4, 6# expert 1 负责: index 1, 2, 7# expert 2 负责: index 3, 5# 所以 按专家编号分组排序后的索引是：idxs = [0, 4, 6, 1, 2, 7, 3, 5]# 这些索引是token（复制top_k倍后）的索引

• Step 2: token_idxs = idxs // top_k

idxs = [0, 4, 6, 1, 2, 7, 3, 5]top_k = 2token_idxs = = idxs // top_k = [0, 2, 3, 0, 1, 3, 1, 2]# 意思是这些位置的 token index（被专家处理的）：# token idx=0 → 原始 token 0# token idx=4 → 原始 token 2# token idx=6 → 原始 token 3# ...

因为 flat_expert_indices 是对 token 被复制分配之后的顺序排列，我们知道每个原始 token 复制了 top_k=2 次，所以：

位置（flat_expert_indices的索引）	对应原始token
0, 1	token 0
2, 3	token 1
4, 5	token 2
6, 7	token 3

所以只要对 token index 整除 top_k 就能还原它是哪个 token。

• Step 3: tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)

flat_expert_indices = [0, 1, 1, 2, 0, 2, 0, 1]# 每个专家被多少 token 分配到（按复制计算）：# expert 0 → 3 次，expert 1 → 3 次，expert 2 → 2 次tokens_per_expert = [3, 6, 8]  # 前缀和：分割 token 的分配区间

Step 4: 依次送入每个专家处理：

Expert 0：

分配到 idxs[0:3] = [0, 4, 6]对应 token_idxs = [0, 2, 3] → 原始 token 的 index从 x 取出 x[0], x[2], x[3] → 做前向输出乘上 gate 权重 [0.9], [0.4], [0.5]加到 expert_cache 的位置 0, 2, 3

Expert 1：

idxs[3:6] = [1, 2, 7]token_idxs = [0, 1, 2]取出 x[0], x[1], x[2]输出乘上 [0.1], [0.3], [0.5]累加到 expert_cache 的位置 0, 1, 2

Expert 2：

idxs[6:8] = [3, 5]token_idxs = [1, 3]取出 x[1], x[3]输出乘上 [0.7], [0.6]累加到 expert_cache 的位置 1, 3

expert_cache最终就是所有专家处理过的结果的加权累加和，每个token位置被多个专家处理，最后叠加权重输出。

最后，对训练和推理阶段的MOE执行过程做一个对比：

方面	训练阶段（Training）	推理阶段（Inference）
Token 是否复制	是，每个 token 被复制 top_k 次	否
处理顺序	每个 token 独立送入专家	将所有 token 按专家分组批量处理
加权方式	top_k 输出加权平均	用 scatter_add_() 加权累加
效率	低（但梯度计算方便）	高（节省内存，计算高效）
适用场景	训练	推理（部署）
多专家叠加	加权平均	加权叠加

2.2 MOE的负载均衡

这部分主要参考了：

https://ai.gopubby.com/deepseek-v3-explained-3-auxiliary-loss-free-load-balancing-4beeb734ab1f

https://www.linkedin.com/pulse/what-main-benefit-mixture-experts-moe-models-qi-he-nkgbe?utm_source=rss&utm_campaign=articles_sitemaps&utm_medium=google_news

在MOE_Gate打分的时候，可能偏向于给某几个专家打高分，导致token总是交给这几个专家处理，其余的专家总是处于空闲状态，这就是负载的不均衡，也称之为路由坍塌(Route collapse)。

路由坍塌的存在，会影响最终的模型效果。具体来说，由于过载的专家接收更多的输入token，它们也会积累更大的梯度，并且比负载较轻的专家学习得更快。结果，过载的专家和负载较轻的专家的梯度在幅度和方向上可能会发散，使得训练过程更难收敛。

为了实现专家的负载均衡，有许多不同的技术被提出来以处理这个问题。

2.2.1 专家选择(Expert Choice)

在原始的MOE中，是每个token给出对于所有专家的打分，然后每个token各自选出得分top_k大的top_k个专家，这是一个token选择专家的过程。负载不均衡指的就是某些专家一直没有被token选择。

Expert Choice将原先的“token选择专家”改成“专家选择要处理的token”：

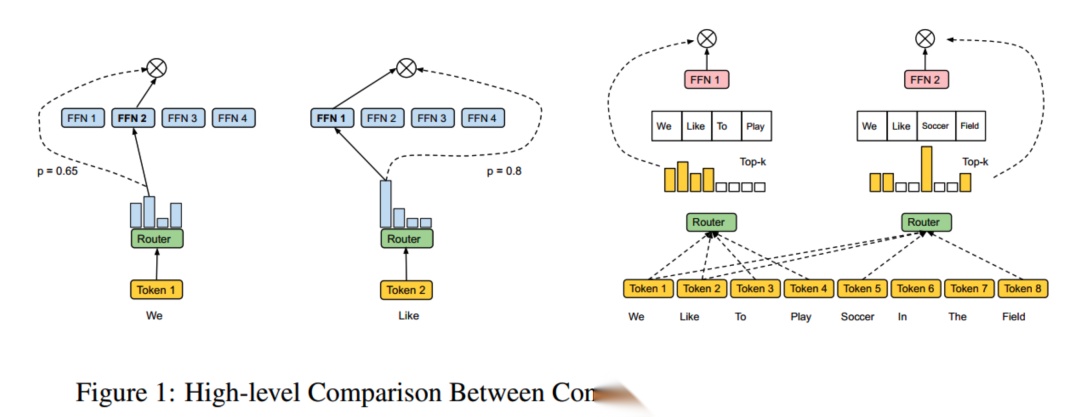
每个专家都预先设置一个专家容量k，因此不会出现某些专家一直没有token可处理的情况。

然而，这种方法也有可能出现某些token使用了多个专家，而有些token只使用了很少甚至0个专家的情况。

2.2.2 辅助损失

在MiniMind源码中使用的是辅助损失的方式来应对路由坍塌问题。

在计算出每个token对于所有专家的打分后，每个token会选择top_k个得分高的专家进行后续处理。我们可以根据这里每个专家的得分（平均打分），以及每个专家实际被选中使用的频率（实际负载），来定义损失函数。具体来说，如果每个专家频繁被选中，并且每个专家的得分总是高于其它专家，那么就会惩罚这个专家。由于此时该专家对应的“平均打分 x 实际负载”比较高，将这个乘积作为一项loss进行惩罚。

基于这种思想，MiniMind分别从序列维度和整个batch维度进行了上述辅助损失函数的实现，相应的解释已经写在代码注释中，如下：

class MoEGate(nn.Module):    def __init__(self, config):        super().__init__()        self.config = config        self.top_k = config.num_experts_per_tok                    # 每个 token 分配的专家个数        self.n_routed_experts = config.n_routed_experts           # 总可选专家数        self.scoring_func = config.scoring_func                   # 评分函数（仅支持 softmax）        self.alpha = config.aux_loss_alpha                        # 辅助损失权重        self.seq_aux = config.seq_aux                             # 是否使用序列级辅助损失        self.norm_topk_prob = config.norm_topk_prob               # 是否对 top-k 权重归一化        self.gating_dim = config.hidden_size                      # gating 输入维度        self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))  # [n_experts, hidden_dim]        self.reset_parameters()    def reset_parameters(self) -> None:        import torch.nn.init as init        init.kaiming_uniform_(self.weight, a=math.sqrt(5))    def forward(self, hidden_states):        """        Args:            hidden_states: [bsz, seq_len, hidden_dim]        Returns:            topk_idx: [bsz * seq_len, top_k] - top-k 专家索引            topk_weight: [bsz * seq_len, top_k] - top-k 专家对应的权重            aux_loss: scalar - 辅助损失，用于平衡专家负载        """        bsz, seq_len, h = hidden_states.shape        hidden_states = hidden_states.view(-1, h)                     # [bsz * seq_len, hidden_dim]        logits = F.linear(hidden_states, self.weight, None)          # [bsz * seq_len, n_experts]        if self.scoring_func == 'softmax':            scores = logits.softmax(dim=-1)                          # [bsz * seq_len, n_experts]        else:            raise NotImplementedError(f'insupportable scoring function for MoE gating: {self.scoring_func}')        topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)  # 都是 [bsz * seq_len, top_k]        if self.top_k > 1and self.norm_topk_prob:            denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20            topk_weight = topk_weight / denominator                  # [bsz * seq_len, top_k]        # ========== Auxiliary Loss for Load Balancing ==========        if self.training and self.alpha > 0.0:            scores_for_aux = scores                                  # [bsz * seq_len, n_experts]            aux_topk = self.top_k            topk_idx_for_aux_loss = topk_idx.view(bsz, -1)           # [bsz, seq_len * top_k]            if self.seq_aux:  # 按 batch 维度分别计算每个样本内部的 expert 使用分布                scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)   # [bsz, seq_len, n_experts]，按 batch 还原 gating scores                ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device)  # 初始化每个 batch 的 expert 统计图 [bsz, n_experts]                ce.scatter_add_(                    dim = 1,                    index = topk_idx_for_aux_loss,                           # [bsz, seq_len * top_k]，每个样本所有 token 的 top_k expert 索引                    src = torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)  # [bsz, seq_len * top_k]，所有位置计数为1                ).div_(seq_len * aux_topk / self.n_routed_experts)          # 标准化：理论上每个 expert 的理想负载是平均的 => 除以 (seq_len * top_k / n_experts)                # aux_loss 越大说明 score 分布与使用频率越不匹配（某些 expert 被打分高且被频繁使用）                aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha                  # - scores_for_seq_aux.mean(dim=1): [bsz, n_experts]，每个样本对每个 expert 的平均打分                # - ce: 每个 expert 的归一化使用频率，越接近1说明越平均                # - ce * score：频率高且分数高则惩罚高                # - 最终 loss 对 batch 取平均，乘 alpha            else:                mask_ce = F.one_hot(                      # one-hot 编码每个 token 被选中的 expert                    topk_idx_for_aux_loss.view(-1),      # [bsz * seq_len * top_k]，flatten 后的所有 expert 索引                    num_classes=self.n_routed_experts    # one-hot 中 expert 数量                )  # => [bsz * seq_len * top_k, n_experts]                ce = mask_ce.float().mean(0)              # [n_experts]，每个 expert 被使用的频率（除以总 token 数量）                Pi = scores_for_aux.mean(0)               # [n_experts]，所有 token 对各 expert 的平均打分                fi = ce * self.n_routed_experts           # 频率 × expert 数 = 负载比，理想负载为1，偏离表示不均                aux_loss = (Pi * fi).sum() * self.alpha   # aux_loss = sum(Pi[i] * fi[i])，高打分 + 高负载的 expert 会被惩罚                # - Pi: 平均打分，值越大说明 router 趋向于使用该 expert                # - fi: 实际负载，值越大说明该 expert 被频繁使用                # - Pi * fi：打分高且频率高的 expert 会导致更大的 loss（目标是让负载更均匀）        else:            aux_loss = 0        return topk_idx, topk_weight, aux_loss

AI时代，未来的就业机会在哪里？

答案就藏在大模型的浪潮里。从ChatGPT、DeepSeek等日常工具，到自然语言处理、计算机视觉、多模态等核心领域，技术普惠化、应用垂直化与生态开源化正催生Prompt工程师、自然语言处理、计算机视觉工程师、大模型算法工程师、AI应用产品经理等AI岗位。

掌握大模型技能，就是把握高薪未来。

那么，普通人如何抓住大模型风口？

AI技术的普及对个人能力提出了新的要求，在AI时代，持续学习和适应新技术变得尤为重要。无论是企业还是个人，都需要不断更新知识体系，提升与AI协作的能力，以适应不断变化的工作环境。

因此，这里给大家整理了一份《2025最新大模型全套学习资源》，包括2025最新大模型学习路线、大模型书籍、视频教程、项目实战、最新行业报告、面试题等，带你从零基础入门到精通，快速掌握大模型技术！

由于篇幅有限，有需要的小伙伴可以扫码获取！

1. 成长路线图&学习规划

要学习一门新的技术，作为新手一定要先学习成长路线图，方向不对，努力白费。这里，我们为新手和想要进一步提升的专业人士准备了一份详细的学习成长路线图和规划。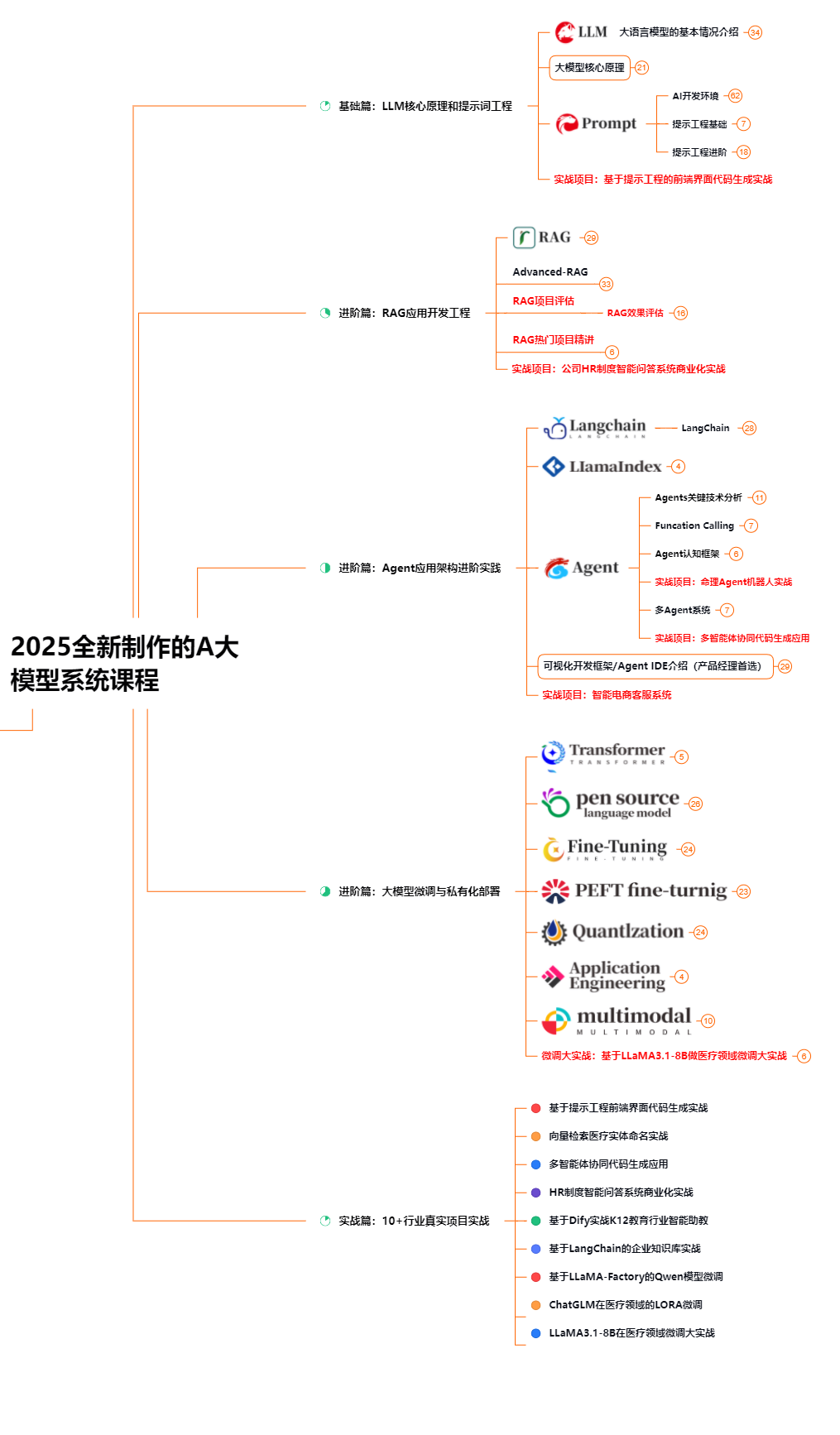

2. 大模型经典PDF书籍

书籍和学习文档资料是学习大模型过程中必不可少的，我们精选了一系列深入探讨大模型技术的书籍和学习文档，它们由领域内的顶尖专家撰写，内容全面、深入、详尽，为你学习大模型提供坚实的理论基础。（书籍含电子版PDF）

3. 大模型视频教程

对于很多自学或者没有基础的同学来说，书籍这些纯文字类的学习教材会觉得比较晦涩难以理解，因此，我们提供了丰富的大模型视频教程，以动态、形象的方式展示技术概念，帮助你更快、更轻松地掌握核心知识。

4. 大模型项目实战

学以致用 ，当你的理论知识积累到一定程度，就需要通过项目实战，在实际操作中检验和巩固你所学到的知识，同时为你找工作和职业发展打下坚实的基础。

5. 大模型行业报告

行业分析主要包括对不同行业的现状、趋势、问题、机会等进行系统地调研和评估，以了解哪些行业更适合引入大模型的技术和应用，以及在哪些方面可以发挥大模型的优势。

6. 大模型面试题

面试不仅是技术的较量，更需要充分的准备。

在你已经掌握了大模型技术之后，就需要开始准备面试，我们将提供精心整理的大模型面试题库，涵盖当前面试中可能遇到的各种技术问题，让你在面试中游刃有余。

为什么大家都在学AI大模型？

随着AI技术的发展，企业对人才的需求从“单一技术”转向 “AI+行业”双背景。企业对人才的需求从“单一技术”转向 “AI+行业”双背景。金融+AI、制造+AI、医疗+AI等跨界岗位薪资涨幅达30%-50%。

同时很多人面临优化裁员，近期科技巨头英特尔裁员2万人，传统岗位不断缩减，因此转行AI势在必行！

这些资料有用吗？

这份资料由我们和鲁为民博士(北京清华大学学士和美国加州理工学院博士)共同整理，现任上海殷泊信息科技CEO，其创立的MoPaaS云平台获Forrester全球’强劲表现者’认证，服务航天科工、国家电网等1000+企业，以第一作者在IEEE Transactions发表论文50+篇，获NASA JPL火星探测系统强化学习专利等35项中美专利。本套AI大模型课程由清华大学-加州理工双料博士、吴文俊人工智能奖得主鲁为民教授领衔研发。

资料内容涵盖了从入门到进阶的各类视频教程和实战项目，无论你是小白还是有些技术基础的技术人员，这份资料都绝对能帮助你提升薪资待遇，转行大模型岗位。

大模型全套学习资料已整理打包，有需要的小伙伴可以微信扫描下方CSDN官方认证二维码，免费领取【保证100%免费】