核心目标：从"预测点"到"理解可能性”

传统行为克隆（BC）学习一个函数$f:a=f(o)$，输出一个唯一的动作点。生成模型（VAEs）学习的是联合概率分布$p(o,a)$，输出的是所有可能 $(o,a)$ 对的可能性。

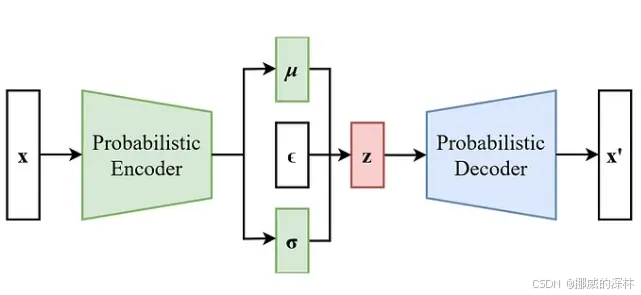
0. VAE 组件：

Encoder: Maps input data to a latent space, producing mean and variance vectors.
编码器：将输入数据映射到潜在空间，生成均值和方差向量。
Latent Space: Represents the compressed features of the data (mean and variance form a Gaussian distribution).
Latent Space：表示数据的压缩特征（均值和方差形成高斯分布）。
Decoder: Reconstructs data from the latent space, generating new data samples from the distribution.
解码器：从潜在空间重建数据，从分布生成新的数据样本。

Step 2: Define the VAE Architecture
第 2 步：定义 VAE 架构
class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        
        # Encoder: Input -> Hidden layers
        self.fc1 = nn.Linear(28*28, 400)  # Flattened input 
        self.fc21 = nn.Linear(400, 20)    # Mean of the latent space 生成均值
        self.fc22 = nn.Linear(400, 20)    # Log-variance of the latent space 对数方差 (

        # Decoder: Latent space -> Output
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 28*28)  # Output size

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)  # Mean and log-variance

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)  # Standard deviation
        eps = torch.randn_like(std)    # Sample epsilon
        return mu + eps * std          # Reparameterization trick

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return torch.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 28*28))  # Flatten input
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

# VAE Loss Function
def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 28*28), reduction='sum')
    # KL Divergence term
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE + KLD


import matplotlib.pyplot as plt
Step 5: Generating New Data from Latent Space
第 5 步：从潜在空间生成新数据
model.eval()
with torch.no_grad():
    # Sample random points in latent space
    z = torch.randn(64, 20).to(device)
    sample = model.decode(z).cpu()

    # Visualize some generated images
    sample = sample.view(64, 1, 28, 28)
    grid_img = torchvision.utils.make_grid(sample, nrow=8)
    plt.imshow(grid_img.permute(1, 2, 0))
    plt.show()

1. 变分自编码器(VAE)基本原理

Note: 变分推断近似的潜在变量模型
在VAE的语境中，“证据”通常指的是$p_{\theta }(X)$，即数据在模型下的概率（边缘似然）。而“所有数据点在参数θ下的对数似然”其实就是对数证据，即$\log p_{\theta }(X)$。但是注意，在VAE中，参数θ是解码器的参数，我们想要最大化所有数据点的对数证据。然而，由于我们无法直接计算对数证据，所以我们转而优化ELBO，因为ELBO是对数证据的下界。

给定一个数据集 $\mathcal{D}$，其中包含 $N$个独立同分布的观测-动作对，所有数据点在参数 $\theta$下的对数似然（在贝叶斯术语中称为证据$p_{\theta }(\mathcal{D})$）可以写为：
$$\begin{gathered} \log p_{\theta }(\mathcal{D})=\log \sum _{i=0}^N{p}_{\theta }((o,a{)}_i) \\ =\log \sum _{i=0}^N{\int }_{\mathrm{supp}(Z)}{p}_{\theta }((o,a{)}_i\mid z)p(z)dz \\ =\log \sum _{i=0}^N{\int }_{\mathrm{supp}(Z)}\frac{q_{\theta }(z\mid (o,a{)}_i)}{q_{\theta }(z\mid (o,a{)}_i)}{p}_{\theta }((o,a{)}_i\mid z)p(z)dz \\ =\log \sum _{i=0}^N{\mathbb{E}}_{z\sim q_{\theta }(\cdot \mid (o,a{)}_i)}\left[\frac{p(z)}{q_{\theta }(z\mid (o,a{)}_i)}{p}_{\theta }((o,a{)}_i\mid z)\right] \end{gathered}$$

其中，我们在公式(20)中使用了公式(19)，在公式中乘以了$1=\frac{q_{\theta }(z|(o,a{)}_i)}{q_{\theta }(z|(o,a{)}_i)}$，在公式中使用了期望值的定义。

我们想要学习模型的参数$\theta$（用于生成模型$p_{\theta }(o,a|z)$）和$\varphi$（用于近似后验分布$q_{\varphi }(z|o,a)$）。因为真实后验$p(z|o,a)$是难以计算的，所以我们使用一个编码器网络$q_{\varphi }(z|o,a)$来近似。

概念： 使用编码器 $q_{\varphi }(z|o,a)$ 来近似推断 $z$。

Robot 实例：

• 假设我们在训练集中拿出一个片段：机器人正紧紧抓住杯子并且向上移动

• 编码器的工作：编码器网络接收这个 $(o,a)$作为输入。它"看"到动作是向上的，且夹爪是闭合的，于是它推断：“这看起来像是在倒水”

• 输出：编码器输出一个分布（比如均值 $\mu$ 和方差 $\sigma$），告诉我们$z$ 很有可能属于"倒水"那个区域

2. 生成器

VAE（变分自编码器）是一种生成模型，它假设观测数据（在机器人操作中，即观测-动作对$(o,a)$）是由一个潜在的变量$z$生成的。这个$z$可以解释为执行任务的高级表示，比如任务类型（如抓取或推动）。

VAE的目标是学习一个模型，能够生成类似于训练数据的观测-动作对，同时学习一个有意义的潜在表示。

我们有一个数据集$\mathcal{D}$，包含$N$个独立同分布的观测-动作对$\{(o,a{)}_i\}$。我们假设每个$(o,a)$是由一个潜在变量$z$生成的，生成过程如下：$$p(o,a)=\int p(o,a|z)p(z)dz$$

其中，$p(z)$是潜在变量的先验分布（通常为标准正态分布），$p(o,a|z)$是条件似然，表示给定$z$时生成$(o,a)$的概率。

概念： 假设观测-动作对 $(o,a)$ 由潜在变量 $z$ 生成。

Robot 实例：

• $o$ (Observation): 机器人摄像头的图像（看到杯子位置）+当前机械臂的角度

• $a$ (Action): 机械臂下一时刻的速度指令（比如向上抬还是向前推）

• $z$ (Latent Variable): 这里 $z$ 代表**“任务的意图”**

  • 如果是"倒水"，$z$ 可能在潜在空间的一个特定区域（例如 $z\approx [1,1]$）

  • 如果是"推杯子"，$z$ 可能在另一个区域（例如 $z\approx [-1,-1]$）

生成过程： 只要确定了 $z$ 是"倒水"，模型 $p(o,a|z)$就会倾向于生成"向上抬升"的动作 $a$，而不是"水平移动"的动作。

3. 如何计算：证据下界（ELBO）

我们无法直接最大化对数似然$\log p_{\theta }(\mathcal{D})$，因为它难以计算。因此，我们转而最大化它的下界，即ELBO。

对于单个数据点$(o,a)$，ELBO为：
$$\text{ELBO}={\mathbb{E}}_{z\sim q_{\varphi }(\cdot |o,a)}\left[\log p_{\theta }(o,a|z)\right]-D_{\text{KL}}\left(q_{\varphi }(z|o,a)\Vert p(z)\right)$$

这个公式可以解释为：

• 第一项是重构项，希望从编码器得到的$z$能够通过解码器很好地重构$(o,a)$

• 第二项是正则项，希望编码器输出的分布$q_{\varphi }(z|o,a)$与先验$p(z)$（标准正态分布）尽可能接近

Robot 实例：

• 重构项 (Reconstruction): 如果编码器认为这是"倒水" ($z$),那么解码器必须能根据这个 $z$ 和当前的图像 $o$，还原出"向上抬"的动作$a$。如果解码器错误地还原成了"向前推"，那么重构误差就会很大

• 正则项 (Regularization): 我们希望"倒水"和"推杯子"的 $z$分布不要太离谱（比如不要跑到无穷远），而是尽量靠近标准正态分布。这保证了潜在空间是连续且平滑的。如果没有这一项，可能$z=100$ 是倒水，$z=-100$是推杯子，中间的区域没有任何意义，导致模型无法生成新动作

4. 重参数化技巧

为了能够通过随机梯度下降优化ELBO，我们需要对$z$进行采样，而采样操作是不可导的。因此，我们使用重参数化技巧：
$$z={\mu }_{\varphi }(o,a)+{\sigma }_{\varphi }(o,a)\cdot \epsilon ,\text{其中 }\epsilon \sim \mathcal{N}(0,I)$$

Robot 实例：

class VAE_DirectSample(nn.Module):
    def __init__(self):
        super(VAE_DirectSample, self).__init__()
        self.fc1 = nn.Linear(28*28, 400)
        self.fc21 = nn.Linear(400, 20)    # mu
        self.fc22 = nn.Linear(400, 20)    # logvar
        
    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)
    
    def direct_sample(self, mu, logvar):
        # 直接采样版本 - 不可导！
        std = torch.exp(0.5 * logvar)
        # 问题在这里：torch.normal 的采样操作不可导
        z = torch.normal(mu, std)  # 直接从 N(mu, std) 采样
        return z
    
    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 28*28))
        z = self.direct_sample(mu, logvar)  # 不可导！
        return self.decode(z), mu, logvar

• 神经网络需要通过反向传播来更新参数。直接"抽签"（采样）是不能求导的

• 操作：编码器预测出"倒水"意图的中心位置 $\mu$ 和不确定性$\sigma$。然后我们从标准噪声 $\epsilon$ 中采样，加上去得到 $z$

• 意义：这就像告诉网络："即使我在你的判断上加一点点随机扰动，你也应该能重构出正确的倒水动作。"这让网络更鲁棒，并且使得整个过程在数学上可导，从而可以训练
  这样，我们可以将梯度反向传播到${\mu }_{\varphi }$和${\sigma }_{\varphi }$。

5. 损失函数

实际上，我们最小化负ELBO，这等价于：
$$\mathcal{L}={\mathcal{L}}_{\text{rec}}+{\mathcal{L}}_{\text{reg}}$$

其中： $$\begin{array}{rl}{\mathcal{L}}_{\text{rec}}& =-{\mathbb{E}}_{z\sim q_{\varphi }(\cdot |o,a)}\left[\log p_{\theta }(o,a|z)\right]\text{（重构损失）}\\ {\mathcal{L}}_{\text{reg}}& =D_{\text{KL}}\left(q_{\varphi }(z|o,a)\Vert p(z)\right)\text{（正则化损失）}\end{array}$$

重构损失通常用均方误差（MSE）来近似，特别是当$p_{\theta }(o,a|z)$被假设为高斯分布时。
正则化损失可以解析地计算，因为两个分布都是高斯分布（假设先验和近似后验都是高斯）。
$$L_{rec}(\theta )=-{\mathbb{E}}_{z\sim q_{\varphi }}[\log p_{\theta }(o,a|z)]$$

• **功能：**这是回归部分。它要求解码器 $p_{\theta }$ 能够利用编码器$q_{\varphi }$ 提供的变量 $z$，完美地重新构造出原始输入 $(o,a)$

• **如何解决问题：**确保模型不会忘记数据本身。如果 $p_{\theta }$被建模为高斯分布，这等价于最小化 $(o,a)$ 和 ${\mu }_{\theta }(z)$之间的欧氏距离，类似于 BC 的回归损失
  $$L_{reg}(\varphi )=D_{KL}[q_{\varphi }(z|o,a)||p(z)]$$

• **功能：**这是概率部分。它要求编码器 $q_{\varphi }$能被赋值信息，并确保学到的变量 $z$ 的分布 $q_{\varphi }$尽可能地接近我们假设的简单先验分布 $p(z)$（通常是标准高斯分布 $\mathcal{N}(0,1)$）

• **如何解决问题：**强制 $z$ 空间具有规律性。这使得 $z$能够成为一个有意义、可插值、可采样的形式空间。在机器人执行任务时，即使遇到$o^{\prime }$（协变量偏移），我们依然可以在这个规范化的 $z$空间中采样一个合理的 $z$，从而生成一个可靠的动作$a\sim p(a|o^{\prime },z)$，帮助解决复合误差
  Robot 实例：

• ${\mathcal{L}}_{\text{rec}}$ (MSE): 比如真实动作是"关节1速度为 0.5rad/s"。如果模型重构出的动作是 0.1 rad/s，那么误差就$(0.5-0.1{)}^2$。我们希望这个误差越小越好

• ${\mathcal{L}}_{\text{reg}}$ (KL散度):这是一个惩罚项。如果编码器把"倒水"的 $z$压缩得像一个针尖一样（方差极小），或者放得离原点太远，KL散度就会变大，迫使网络把分布调整得更像标准正态分布

"如有问题， 请在评论下指正，感谢！“”