本文还有配套的精品资源，点击获取

简介：图像变形是图像处理中的一项技术，通过重新映射原始图像的像素位置来创造出新的视觉效果。本话题将深入探讨如何使用OpenCV库实现图像变形，特别关注等距多项式插值（IDW）和径向基函数（RBF）。这两种方法能够在不同程度和范围内处理图像变形，创建出平滑连续的视觉效果。本课程将引导学生学习如何使用OpenCV中的 cv::warpPerspective() 和 cv::getPerspectiveTransform() 函数，以及如何构建变换矩阵和应用适当的插值算法。图像变形的应用领域包括全景图像创建、镜头畸变校正、虚拟现实场景构建以及艺术效果生成等。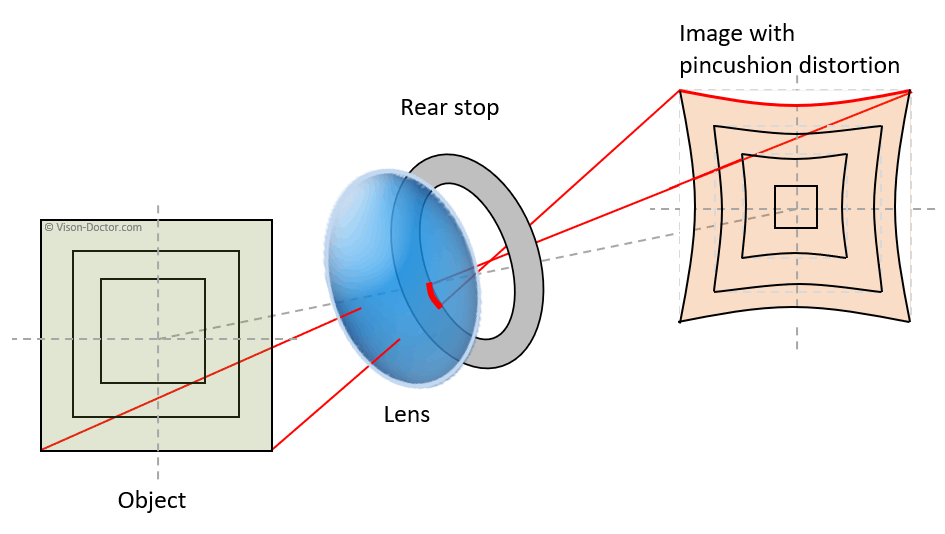

1. 图像变形概念和应用

图像变形基础

图像变形是一种处理技术，允许开发者或设计师通过改变图像的几何结构来达到预期的视觉效果。这种方法广泛应用于图像编辑、计算机视觉、游戏开发和增强现实等领域。在图像变形技术中，原始图像的坐标系统会被映射到新的坐标系统，从而实现形状、大小或视角的变化。

应用场景

图像变形的应用场景十分丰富，如图像缩放、旋转、扭曲、倾斜和透视变形等。这些变形可以用来创建特定的视觉效果，比如在视频制作中模拟相机移动，或者在游戏设计中营造动态场景。更高级的应用还包括医学影像的处理、增强现实中的3D场景构建，以及数字取证中用于识别和恢复图像信息。

变形技术的重要性

图像变形技术对于维持图像内容的视觉连贯性至关重要。正确的变形可以改善图像的质量和外观，而不恰当的变形则可能导致图像失真和细节丢失。因此，深入理解图像变形的基础知识和高级应用是实现高质量图像处理的关键。接下来的章节将详细介绍一些常用的图像变形方法，如等距多项式插值（IDW）和径向基函数（RBF），以及如何利用OpenCV等工具库实现这些技术。

2. 等距多项式插值（IDW）方法

2.1 IDW插值的基本原理

2.1.1 等距性概念与意义

等距多项式插值（Inverse Distance Weighting，IDW）是一种基于空间插值的方法，用于根据一组已知点来估计未知点的值。该方法认为，一个点的属性值受其周围已知点的影响，且这种影响与其距离成反比。换句话说，距离越近的点对未知点的值影响越大。等距性体现在权重的计算上，权重与距离的负幂成正比。这种插值方法在图像变形中的意义在于，它能够根据相邻像素点之间的距离和值来推测出变形后图像中相应像素点的值，从而实现自然的变形效果。

2.1.2 IDW插值在图像变形中的作用

在图像变形中，IDW插值方法用于处理像素点的重新分布。通过IDW插值，能够确保变形后的图像保持像素点间的相对关系，并且避免出现过于尖锐的过渡。这样可以得到更平滑的图像效果，特别是在进行放缩、倾斜等操作时。IDW插值方法可以应用于图像放大时的像素重建，缩小时的像素合并，以及更为复杂的变形操作，如任意形状的扭曲变形。

2.2 IDW插值算法的实现步骤

2.2.1 算法流程解析

IDW插值算法通常包括以下步骤：

1. 确定插值点与已知数据点集合。
2. 计算插值点到各个已知数据点之间的距离。
3. 根据距离计算每个已知数据点对插值点的影响权重。
4. 利用权重和已知数据点的值，计算插值点的估计值。
5. 重复步骤2至4，直到整个图像区域被插值完毕。

2.2.2 权重的计算方法

权重的计算是IDW插值的核心，通常使用以下公式计算：

[ w_i = \frac{1}{d_i^p} ]

其中，( w_i ) 是第 ( i ) 个已知点的权重，( d_i ) 是插值点到已知点 ( i ) 的距离，( p ) 是用户定义的幂参数（一般大于零），用于控制权重随距离变化的速度。

2.2.3 插值效果的优化策略

IDW插值效果的优化主要通过调整幂参数 ( p ) 来实现。较小的 ( p ) 值会导致权重差异较小，使得插值结果较为平滑，可能会忽略局部细节；较大的 ( p ) 值会使靠近插值点的已知点权重急剧增大，保留更多的局部细节，但可能导致插值结果出现“洞”或者边缘效应。因此，选择合适的 ( p ) 值对于优化IDW插值效果至关重要。

代码块展示及解释

import numpy as np
from scipy.interpolate import griddata

# 假设我们有一组已知点的坐标和对应的值
known_points = np.array([
    [1.0, 1.0, 5.0],
    [2.0, 2.0, 7.0],
    [3.0, 4.0, 8.0]
])

# 假设我们要在这些点中插入新的点
unknown_points = np.array([
    [1.5, 1.5],
    [2.5, 2.5]
])

# IDW插值函数
def idw_interpolation(known_points, unknown_points, p):
    # 计算插值点坐标
    x, y = unknown_points.T
    xy = np.vstack((x, y)).T
    # 为每个插值点计算值
    interpolated_values = np.zeros_like(x)
    for i, (xi, yi) in enumerate(zip(xy)):
        # 计算权重
        weights = 1.0 / np.power(known_points[:, :2] - [xi, yi], p)
        # 对已知点的值进行加权求和
        interpolated_values[i] = np.sum(weights * known_points[:, 2]) / np.sum(weights)
    return interpolated_values

# 执行IDW插值
interpolated_values = idw_interpolation(known_points, unknown_points, 2)
print(interpolated_values)

在上述Python代码中，我们首先导入了必要的库，定义了一组已知点和未知点。接着定义了一个 idw_interpolation 函数，它根据已知点、未知点和幂参数 ( p ) 来计算IDW插值。计算权重时，我们使用了向量化操作，这提高了代码的执行效率。最后，我们调用该函数并打印了插值结果。

通过调整 p 值，我们可以观察到插值结果的不同变化，以找到最佳的插值效果。

3. 径向基函数（RBF）插值方法

径向基函数（Radial Basis Function, RBF）插值方法是一种强大的空间插值技术，它在图像变形领域中发挥着重要作用，尤其适用于非规则分布的数据点插值。RBF方法通过使用多个径向对称函数来构建一个表面，使得每一个数据点都能够影响到整个插值曲面。这种方法不仅提供了一种精确插值的方式，同时也赋予了用户高灵活性，能够通过调整函数参数来改善插值质量。

3.1 RBF插值的基本概念

3.1.1 径向基函数的定义与分类

径向基函数是一类定义在多维空间上的实值函数，它们的形式主要取决于空间中某一点到某一特定点（称为“中心点”）的距离。最常用的径向基函数有高斯径向基函数、多二次径向基函数、逆多二次径向基函数、薄板样条径向基函数和Wendland径向基函数等。在这些函数中，高斯径向基函数因其具有良好的插值性能和数学特性，被广泛应用于图像变形技术中。

3.1.2 RBF在图像变形中的应用

RBF插值方法在图像变形中的应用主要体现在它能够提供非常平滑的插值效果。这是因为RBF能够在整个插值区域内提供连续的二阶导数，这对于保持图像质量，尤其是在需要连续变化的图像处理任务中非常关键。通过RBF插值，可以实现图像的缩放、旋转、扭曲等变形效果，同时减少边缘模糊和细节损失。

3.2 RBF插值算法的详细解析

3.2.1 算法实现流程

径向基函数插值算法的实现步骤可以概括为以下几个核心步骤：

1. 选择径向基函数 ：根据具体应用需求选择适合的径向基函数。对于图像变形来说，高斯径向基函数和多二次径向基函数较为常用。
2. 确定中心点 ：这些中心点可以从原始数据点集合中选取，也可以是另外定义的点集合。
3. 计算权重 ：利用插值点和中心点之间的距离来计算对应的权重系数。
4. 构建线性方程组 ：根据权重和径向基函数值构建线性方程组。
5. 求解权重系数 ：通过最小二乘法等数学方法求解上述方程组，得到所有中心点的权重系数。
6. 构造插值函数 ：根据权重系数和径向基函数构建最终的插值函数。

3.2.2 影响RBF插值效果的关键因素

影响RBF插值效果的关键因素主要包括：

• 径向基函数的选择 ：不同的径向基函数适用于不同的场景，某些函数在处理大范围插值时表现更优，而另一些则可能在细节保持上更为出色。
• 中心点的分布和数量 ：中心点的选择和数量直接影响到插值的精度和效率。如果中心点分布过于稀疏，则插值结果可能会出现不平滑的现象；而中心点过多则可能导致计算效率降低。
• 权重计算方法 ：权重的计算方式决定了每个数据点对最终插值结果的贡献程度，其精确度对于插值质量有着显著影响。

3.2.3 算法参数选择与调优

参数选择与调优是RBF插值算法中十分关键的一个环节。下面介绍两个重要的参数及其调整策略：

• 平滑参数（Smoothing Parameter） ：这个参数通常与径向基函数的选择相关联，如高斯函数中的标准差。平滑参数决定了插值函数对数据点的敏感度，调整这个参数可以控制插值曲面的平滑程度。较小的平滑参数值通常会导致插值结果更加接近原始数据点，但可能会引入不必要的波动；而较大的值则会使结果更加平滑，但可能会导致细节丢失。
• 张力参数（Tension Parameter） ：某些径向基函数（如薄板样条）引入了张力参数，这个参数控制了曲面的张力程度。增加张力参数值可以使曲面更加“紧绷”，减少曲面弯曲，反之则使曲面变得更加灵活，能够更好地捕捉数据点的变化。

代码示例：

假设我们使用Python语言和SciPy库中的RBF插值函数。下面是一段示例代码，演示如何使用RBF插值对一组二维数据进行插值处理：

import numpy as np
from scipy.interpolate import RBFInterpolator

# 假设这是我们的原始数据点，每一行代表一个点，每列代表一个维度
points = np.array([[0, 0], [1, 1], [2, 2]])
values = np.array([0, 1, 2])

# 创建RBF插值器实例，使用高斯径向基函数
rbf = RBFInterpolator(points, values, kernel='gaussian')

# 构建插值网格
xi = np.linspace(0, 2, 100)
yi = np.linspace(0, 2, 100)
xi, yi = np.meshgrid(xi, yi)
zi = rbf(np.vstack((xi.ravel(), yi.ravel())).T).reshape(xi.shape)

# 将插值结果可视化
import matplotlib.pyplot as plt
plt.imshow(zi, extent=[0, 2, 0, 2], cmap='viridis')
plt.scatter(points[:, 0], points[:, 1], c=values, cmap='viridis')
plt.colorbar()
plt.title('RBF Interpolation')
plt.show()

在上述代码中，首先导入了必要的Python库，然后定义了一组用于插值的二维数据点和它们对应的值。我们创建了一个高斯径向基函数插值器实例，并为插值创建了一个网格。最后，我们使用matplotlib库将插值结果可视化。

在本段代码中， RBFInterpolator 是用于构建RBF插值器的函数， points 和 values 分别是原始数据点和对应的值， kernel='gaussian' 指定了使用高斯径向基函数。通过 np.vstack 将网格点堆叠成一个二维数组，然后调用插值器的 __call__ 方法，将这些点转换为插值结果。最后，结果使用matplotlib库进行可视化展示。

4. OpenCV图像变形函数介绍

OpenCV（Open Source Computer Vision Library）是一个开源的计算机视觉和机器学习软件库，它提供了丰富的图像处理和分析功能，以及强大的图形变形工具。在图像变形领域中，OpenCV为开发者提供了很多方便使用的函数，使得图像变形操作变得更加简单和高效。

4.1 OpenCV中的图像变形工具

4.1.1 主要函数概述

OpenCV中的图像变形工具主要包含以下几种函数：

• cv2.resize() ：用于缩放图像。
• cv2.warpAffine() ：用于进行仿射变换，可以实现旋转、平移、缩放等操作。
• cv2.getPerspectiveTransform() 和 cv2.warpPerspective() ：分别用于计算透视变换矩阵和应用该变换矩阵实现图像的透视变换。
• cv2.getRotationMatrix2D() 和 cv2.warpAffine() ：组合使用可以实现图像的旋转操作。
• cv2.undistort() ：用于矫正图像的透镜畸变。

这些函数可以单独使用，也可以组合使用以实现复杂的图像变形效果。

4.1.2 函数参数及配置方法

每个变形函数都有自己的参数和配置方法。以下是 cv2.warpAffine() 函数的参数说明，以及如何使用该函数进行图像旋转的示例：

import cv2
import numpy as np

# 读取图像
image = cv2.imread('image.jpg')

# 计算旋转矩阵
center = (image.shape[1]//2, image.shape[0]//2) # 图像中心点
angle = 45 # 旋转角度
scale = 1.0 # 缩放比例
rotation_matrix = cv2.getRotationMatrix2D(center, angle, scale)

# 应用仿射变换
rotated_image = cv2.warpAffine(image, rotation_matrix, (image.shape[1], image.shape[0]))

# 显示图像
cv2.imshow('Rotated Image', rotated_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

4.2 OpenCV函数在图像变形中的应用实例

4.2.1 实例分析：图像缩放与旋转

在实际应用中，我们常常需要对图像进行缩放或旋转操作。以下是如何使用OpenCV中的 cv2.resize() 和组合 cv2.getRotationMatrix2D() 与 cv2.warpAffine() 实现图像的缩放与旋转：

# 图像缩放
resized_image = cv2.resize(image, (new_width, new_height))

# 图像旋转
angle = -20 # 逆时针旋转20度
scale = 1.0 # 保持大小不变
rotation_matrix = cv2.getRotationMatrix2D(center, angle, scale)
rotated_image = cv2.warpAffine(image, rotation_matrix, (image.shape[1], image.shape[0]))

4.2.2 实例分析：图像扭曲效果

图像扭曲是图像变形中比较复杂的一种操作，可以通过 cv2.warpAffine() 函数结合不同的变换矩阵来实现。这里提供一个简单的图像扭曲示例，例如，将图像的一个角扭曲到中间：

# 创建扭曲矩阵
distortion_center = (image.shape[1]//2, image.shape[0]//2)
distortion_matrix = np.float32([[1, 0, -distortion_center[0]],
                                [0, 1, -distortion_center[1]],
                                [0, 0, 1]])
distorted_image = cv2.perspectiveTransform(image, distortion_matrix)

# 与原图混合，得到扭曲效果
distorted混合 = cv2.addWeighted(image, 0.5, distorted_image, 0.5, 0)

通过这些OpenCV函数，我们可以实现一系列图像变形操作，从而满足不同的应用场景需求。下面的章节会进一步探讨变换矩阵的构建与应用，以及插值算法在图像变形中的实现和理解。

5. 变换矩阵的构建与应用

5.1 变换矩阵的基本理论

5.1.1 矩阵在图像变形中的作用

变换矩阵是图像变形技术中的核心概念。在计算机图形学中，变换矩阵用于实现图像的几何变换，例如平移、旋转、缩放和扭曲等。它们通过线性代数的方式来描述图像中的点如何被映射到新的位置。图像的每个像素点都可以看作是坐标系中的一个点，通过变换矩阵，这些点的位置可以被重新计算，从而实现图像的变形。

变换矩阵的数学定义是基于线性变换的理论，这些变换通常包括线性变换（如旋转和缩放）和仿射变换（如倾斜和剪切）。在二维空间中，这些变换可以用2x3的矩阵表示，而在三维空间中，变换矩阵通常是4x4的。

5.1.2 常见变换矩阵类型与特点

平移变换矩阵 ：用于在指定方向移动图像的像素点。
[ T = \begin{bmatrix}
1 & 0 & x \
0 & 1 & y \
0 & 0 & 1
\end{bmatrix} ]
其中，(x)和(y)是水平和垂直方向上的平移距离。

旋转变换矩阵 ：用于围绕一个轴旋转图像的像素点。
[ R = \begin{bmatrix}
\cos(\theta) & -\sin(\theta) & 0 \
\sin(\theta) & \cos(\theta) & 0 \
0 & 0 & 1
\end{bmatrix} ]
其中，(\theta)是旋转角度。

缩放变换矩阵 ：用于对图像进行缩小或放大。
[ S = \begin{bmatrix}
s_x & 0 & 0 \
0 & s_y & 0 \
0 & 0 & 1
\end{bmatrix} ]
其中，(s_x)和(s_y)分别是水平和垂直方向上的缩放因子。

剪切变换矩阵 ：用于使图像在水平或垂直方向上倾斜。
[ H = \begin{bmatrix}
1 & k_x & 0 \
k_y & 1 & 0 \
0 & 0 & 1
\end{bmatrix} ]
其中，(k_x)和(k_y)分别是水平和垂直方向上的剪切因子。

这些变换矩阵可以组合使用以实现复杂的图像变形效果。例如，一个图像可以先旋转再平移，组合后的变换矩阵是旋转矩阵和平移矩阵的乘积。

5.2 构建变换矩阵的步骤与技巧

5.2.1 矩阵构建方法

构建变换矩阵的基本步骤如下：

1. 定义变换需求 ：明确图像需要进行的变换类型，如旋转、缩放、平移等。
2. 确定变换参数 ：根据变换需求，确定对应的变换参数，如旋转角度、缩放因子等。
3. 构建基础矩阵 ：根据变换类型选择相应的基础矩阵模板。
4. 参数替换 ：将步骤2中确定的变换参数填入基础矩阵模板中。
5. 矩阵相乘 ：如果需要进行多重变换，将各个变换矩阵按顺序相乘，得到最终的变换矩阵。

例如，要创建一个先向右平移10个像素，然后顺时针旋转45度的变换矩阵，可以先构建平移矩阵和旋转矩阵：
[ T = \begin{bmatrix}
1 & 0 & 10 \
0 & 1 & 0 \
0 & 0 & 1
\end{bmatrix} ]
[ R = \begin{bmatrix}
\cos(45^\circ) & -\sin(45^\circ) & 0 \
\sin(45^\circ) & \cos(45^\circ) & 0 \
0 & 0 & 1
\end{bmatrix} ]
然后将这两个矩阵相乘得到最终的变换矩阵：
[ M = T \times R ]

5.2.2 矩阵应用实例解析

假设我们有一个4x4的图像像素矩阵，用以下矩阵表示：
[ P = \begin{bmatrix}
p_{11} & p_{12} & p_{13} & p_{14} \
p_{21} & p_{22} & p_{23} & p_{24} \
p_{31} & p_{32} & p_{33} & p_{34} \
p_{41} & p_{42} & p_{43} & p_{44}
\end{bmatrix} ]
我们的目标是对这个图像应用前面构建的变换矩阵(M)。

通过矩阵乘法，我们可以将变换矩阵应用于图像矩阵：
[ P’ = M \times P ]
其中，(P’)表示变换后的图像矩阵。实际上，这种乘法将每个像素点的位置通过变换矩阵进行新的坐标计算。

这种变换会在像素间产生空白区域，这种现象称为重采样。为了避免这种现象，我们通常需要在变换前对图像进行插值处理，这将在后续的章节中详细讨论。

变换矩阵的构建与应用是图像变形技术的基础，通过掌握不同的变换矩阵和构建技巧，可以灵活实现各种图像处理效果。下一节将通过具体的代码示例，深入展示变换矩阵的构建与应用过程。

6. 插值算法的实现与理解

插值算法在图像变形中的重要性不言而喻，它们是实现图像放缩、旋转和其他变换效果的核心技术。理解插值算法的目标、原理和实现方法对于图像处理人员来说是必不可少的。

6.1 插值算法在图像变形中的重要性

6.1.1 插值算法的基本目标

插值算法的基本目标是在已知数据点的基础上，估计出未知数据点的值。在图像变形中，这意味着通过已知的像素值来估计变形后新位置的像素值。高质量的插值算法可以减少图像的失真，提高图像变形的准确性，使视觉效果更加自然和平滑。

6.1.2 插值算法与图像质量的关联

插值算法的选取对图像质量有直接影响。不同类型的插值算法会以不同的方式处理图像像素，从而影响最终图像的视觉质量。例如，最近邻插值可能会产生块状效果，而双线性和三次卷积插值则能提供更平滑的图像。因此，理解不同插值算法的优缺点，并根据具体应用场景选择合适的插值算法，对于专业人员来说至关重要。

6.2 插值算法的深入分析与案例

6.2.1 常用插值算法比较

在图像变形的应用中，常用插值算法有最近邻、双线性、双三次等。最近邻插值简单快速，但会产生锯齿状的边缘。双线性插值在处理非整数倍缩放时能够产生更平滑的结果，但可能会模糊细节。双三次插值在提供光滑效果的同时，尽可能保留了图像的细节，但计算代价较高。

6.2.2 实际应用场景案例研究

以图像缩放为例，可以分别使用最近邻、双线性和双三次插值进行处理，并比较结果。以下是使用Python代码和OpenCV库进行实验的示例：

import cv2
import numpy as np

# 加载原始图像
image = cv2.imread('original_image.jpg')

# 获取原始图像尺寸
height, width = image.shape[:2]

# 设置缩放比例
scale = 0.5

# 使用不同的插值方法进行图像缩放
nearest_neighbour = cv2.resize(image, (int(width * scale), int(height * scale)), interpolation=cv2.INTER_NEAREST)
bilinear = cv2.resize(image, (int(width * scale), int(height * scale)), interpolation=cv2.INTER_LINEAR)
bicubic = cv2.resize(image, (int(width * scale), int(height * scale)), interpolation=cv2.INTER_CUBIC)

# 显示结果
cv2.imshow('Nearest Neighbour', nearest_neighbour)
cv2.imshow('Bilinear', bilinear)
cv2.imshow('Bicubic', bicubic)
cv2.waitKey(0)
cv2.destroyAllWindows()

通过以上代码，我们可以直观地观察到不同插值算法在图像缩放中的效果差异。最近邻插值保留了更多原始像素的值，但图像细节较少；双线性插值在细节和平滑度之间取得了较好的平衡；双三次插值提供了最平滑的结果，同时也保留了较多的细节。

通过比较这些案例，我们能够深入理解插值算法在图像变形中的应用和重要性，以及如何根据不同的需求选择合适的插值方法。

本文还有配套的精品资源，点击获取

简介：图像变形是图像处理中的一项技术，通过重新映射原始图像的像素位置来创造出新的视觉效果。本话题将深入探讨如何使用OpenCV库实现图像变形，特别关注等距多项式插值（IDW）和径向基函数（RBF）。这两种方法能够在不同程度和范围内处理图像变形，创建出平滑连续的视觉效果。本课程将引导学生学习如何使用OpenCV中的 cv::warpPerspective() 和 cv::getPerspectiveTransform() 函数，以及如何构建变换矩阵和应用适当的插值算法。图像变形的应用领域包括全景图像创建、镜头畸变校正、虚拟现实场景构建以及艺术效果生成等。

本文还有配套的精品资源，点击获取