在传统的数据分析范式中，我们习惯于处理序列与表格——这些线性或扁平化的结构。

然而，现实世界中的复杂系统，从社交网络、生物化学分子到知识图谱和推荐系统，

其内在关系本质上是非线性、高维关联的。图：节点 + 连边。

将图视为数据分析的基本单元，引出了一个核心挑战：如何量化图的相似性？

 即，如何定义两张图之间的“距离”？这个问题的解答是图聚类、图分类与图检索等高级任务的基石。

当前的主流方法主要沿着两条路径演进：

1. 基于结构的精确匹配：通过子图同构或图编辑距离等概念，追求对图结构差异的精确度量。这类方法计算代价高昂，但具有坚实的理论根基和明确的物理意义。

2. 基于特征的近似度量：通过提取图的统计特征（如拓扑指数）或利用图核函数，将图映射为特征空间中的向量，从而将图相似性问题转化为向量距离计算。这种方法牺牲了部分精确性，但获得了应对大规模图数据的可扩展性。

本文将系统梳理这些关键技术与算法，探讨如何在图的复杂结构与可计算的相似性度量之间建立桥梁，为后续的图数据挖掘任务奠定基础。

目录

1. Subgragh Matching 子图匹配

1.1 Ullmann

1.2 MCG 最大公共子图

1.3 MCG-based Distance 由 MCG 定义两张图的距离

1.4 5个操作 编辑距离

2. 图特征距离

3. 频繁子图 -> Graph Apriori

---

1. Subgragh Matching 子图匹配

问题定义：给定一个大的目标图 G 和一个较小的查询图 Q，找到 G 中所有与 Q 同构的子图。

同构意味着存在一个从 Q 到 G 的子图的双射，使得节点标签和边关系完全一致。

应用场景：

• 化学信息学：在分子结构图（目标图 G）中寻找特定的官能团，如苯环（查询图 Q）。

• 社交网络分析：在社交关系图中寻找稳定的“小团体”，如4个用户两两互为好友的团簇结构。

1.1 Ullmann

问题即为 Q 中每个点映射对应到 G 上的哪个点。

核心数据结构：维护邻接矩阵 M = |Q|*|G| 代表可不可能映射，帮助进行循环搜索和筛选。

度过滤：如果 qi 的度数高于 Gj，Gj 没有足够的连边（就像凹槽按不进去）一定不可能映射。

搜索：逐个分配 Q 中的点，

若 M[i][j] = 1，进行映射，对原来矩阵 M 进行更新。 先 M' = M，再用邻居约束更新。

邻居约束剪枝：如果 qi 映射到了gj，那么对于任何与 qi ​相连的查询图节点 qk​，

                         它在目标图中映射的候选节点 gl 必须是与 gj ​相连的。

实现：若原来 M'[k][l] = 1，但是 (i,k) 连，(j,l)不连，则 M'[k][l] 要置为0.

启发式优化：为了更快地剪枝，搜索顺序至关重要。通常优先选择标签稀有或度数高的查询图节点开始匹配，因为这些节点的候选集较小，能迅速排除大量无效分支。

1.2 MCG 最大公共子图

如果两个图不是子图同构关系，我们退而求其次，寻找它们的最大公共子图。

启发式选筛选 没塞过的边集 C；

枚举每条边，如果塞进当前的匹配 M 之后还是公共子图，继续dfs 并更新答案。

1.3 MCG-based Distance 由 MCG 定义两张图的距离

未匹配部分大小：

标准化一下：没匹配的 / 并集大小

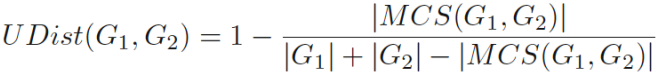
1.4 5个操作 编辑距离

5个操作种类：节点插入/删除；边插入/删除；节点标签更改。

计算思路：可以看作是从公共子图开始，通过编辑操作进行扩展。

1. 限制：最开始只删，最后再做改+插入，G1 -> sub(G1) -> G2

2. 如果G1是G2子图，答案就是加剩下的边数。

启发式优化：

• 避免循环操作：禁止“先删除再添加”同一元素的反悔操作。

• 标签一致性：只在节点标签相同时才考虑添加边，减少无效分支。

• 分支定界：在DFS搜索中，当前累积代价已经超过已知的最优解，提前终止。

对于动作集合 C，先启发式的把价值高的动作筛一遍。

然后 枚举不同动作，dfs(G1',G2,步数)，得到最优步数。

2. 图特征距离

对于大规模图，计算精确的子图匹配或编辑距离不现实。因此，我们转向提取图的全局或局部特征，通过比较特征向量来计算距离。

Transformation-based graph distance（基于变换的图距离）

描述图的一些特征指标：

• 摩根指数：每个节点 “周围 k 步内有多少个节点”，把所有节点的情况统计成表格。
• 维纳指数：图里 “任意两个节点之间的最短路径长度” 总和。
• 保谷指数：图里 “能配对的节点”组数。
• 埃斯特拉达指数：图的 “连接矩阵” 的特征值，指数求和。
• 回路秩：要把图里的 “环” 都去掉，最少得删多少条边？（代表图的 “连接紧密程度”）
• 兰迪奇指数：把图里每两个节点的 “度数”相乘、开根号，再取倒数求和。

图核函数 Graph kernels -> 可以做图核 SVM

例1：随机游走核 co-random walks

• 思路：如果两个图里 “随机走出来的节点序列很像”，那这两个图就很像。
• 具体操作：把两个图 “合并” 成一个 “乘积图”。

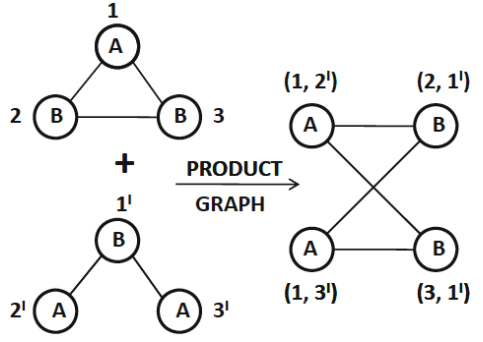
例2：最短路径核

1. 分别计算图 G 和 G′ 中所有节点对之间的最短路径长度矩阵。

2. 将这些路径长度统计成两个直方图 D 和 D′。

3. 通过计算直方图之间的相似度（如交集、卡方距离等）来定义图相似度。

3. 频繁子图 -> Graph Apriori

k-子图可以是节点也可以是边（共享 k 个节点或者共享 k 条边）

1. 生成候选：从频繁的 (k-1)-子图通过连接、扩展等方式生成候选的 k-子图。

2. 剪枝：检查候选k-子图的所有 (k-1)-子图是否都是频繁的。

3. 计数：扫描数据库，计算每个候选k-子图的支持度。

4. 迭代：重复以上步骤，直到不能再生成更大的频繁子图。