🌟 隐马尔可夫模型（HMM）前向算法最通俗的理解

隐马尔可夫模型（HMM）是序列问题中最经典的模型之一。
如果你第一次接触 HMM 的前向算法（Forward Algorithm），可能会被公式吓到：

$${\alpha }_t(i)=\left[\sum _{j=1}^N{\alpha }_{t-1}(j)P(s_i|s_j)\right]\times P(o_t|s_i)$$

其实它的含义 非常生活化、非常直观。
本文用生活例子 + 图像化思维，把 HMM 预测过程讲到你“闭眼都能想象”的程度。

---

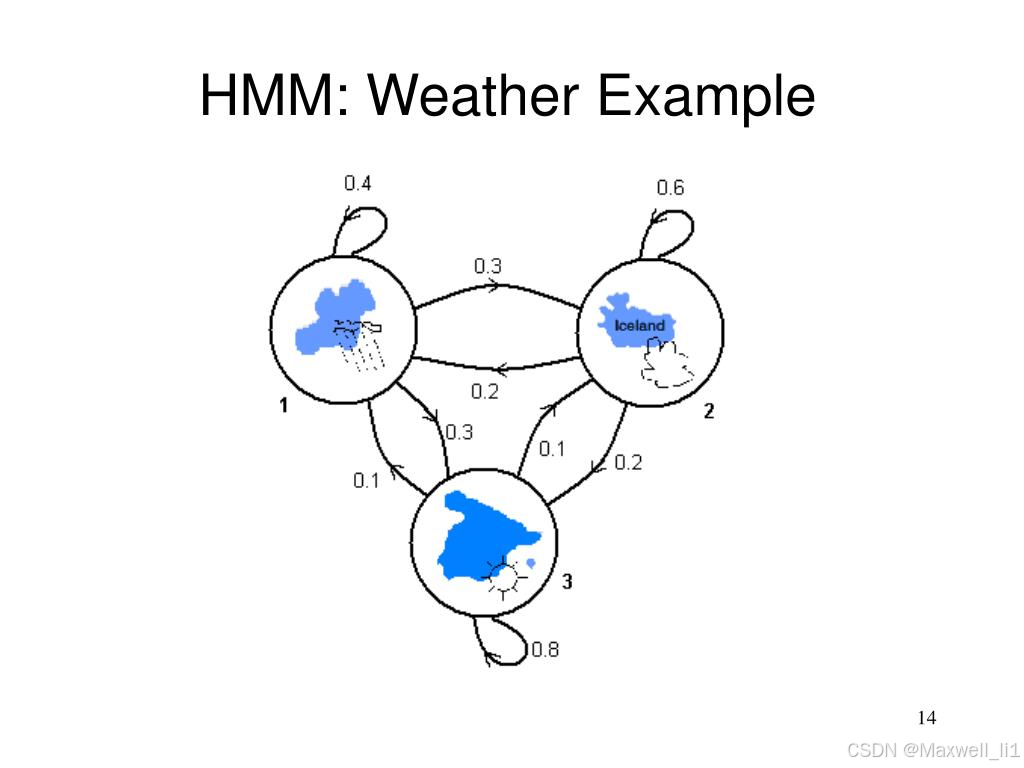
一、HMM 的基本设定（生活类比）

我们用一个极易理解的例子：

• 隐藏状态（你看不到）：天气

  • Sunny
  • Cloud
  • Rain

• 可观测值（你能看到）：别人是否打伞

  • Umbrella
  • No Umbrella

HMM 的作用就是：

虽然你不能看到真正的天气，但你可以通过“是否打伞”的序列，推测这个序列出现的概率有多大。

---

二、前向算法要解决什么问题？

前向算法（Forward Algorithm）计算的是：

$$P(O)=P(\text{观测序列})$$

也就是：

“在这个天气模型下，我们连续看到打伞/不打伞的现象，整体出现的概率是多少？”

比如观测序列是：

[打伞， 打伞， 不打伞]

我们要算这串观测出现的总概率。

看似困难，但前向算法把这个复杂问题拆解为：

每一天可能是 Sunny、Cloud、Rain；
对每种天气，我们计算它通向今天的可能性，再乘以今天的观测概率.

---

三、前向算法的直观过程（不看公式也能懂）

假设观测为：

Day1: 打伞
Day2: 打伞
Day3: 不打伞

对于每一天，我们维护三种天气的概率：

• 今天 Sunny 的可能性
• 今天 Cloud 的可能性
• 今天 Rain 的可能性

每一天都从昨天延伸过来。

---

Step 1：第一天（t=1）

第一天看到“打伞”。
对于每种天气：

$${\alpha }_1(\text{Sunny})=P(\text{Sunny})\times P(\text{打伞}|Sunny)$$

$${\alpha }_1(\text{Cloud})=P(\text{Cloud})\times P(\text{打伞}|Cloud)$$

$${\alpha }_1(\text{Rain})=P(\text{Rain})\times P(\text{打伞}|Rain)$$

这一步完全是“初始概率 × 观测概率”。

---

Step 2：第二天（t=2）

第二天又看到“打伞”。

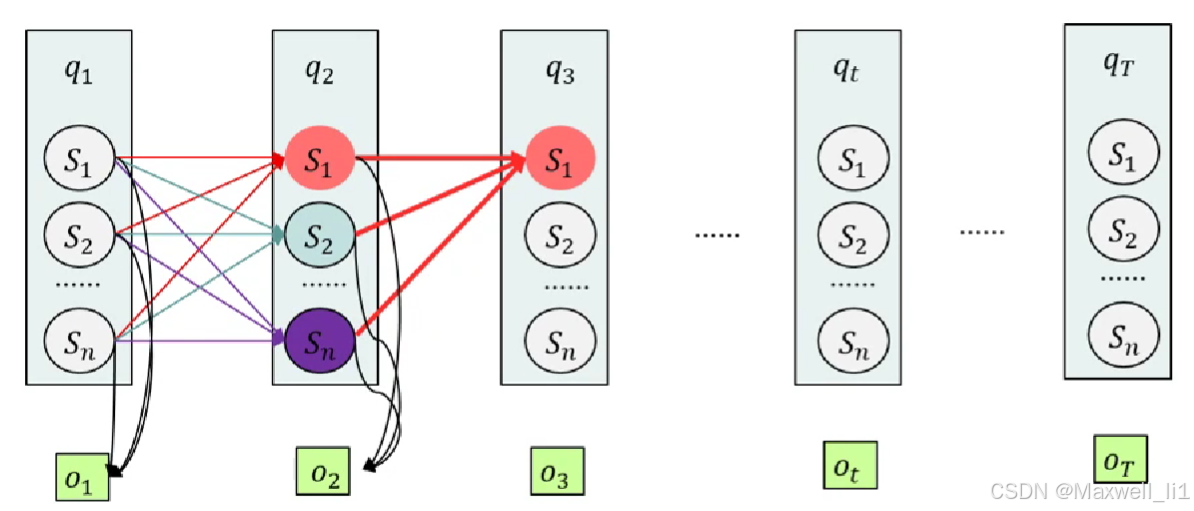
要算“今天是 Sunny”的可能性，必须考虑所有“昨天”的路径：

• 昨天 Sunny → 今天 Sunny
• 昨天 Cloud → 今天 Sunny
• 昨天 Rain → 今天 Sunny

每条路径都有：

昨天该状态的可能性 × 状态转移概率

然后全部加起来：

$$\text{（来自昨天的所有 Sunny 路径）}={\alpha }_1(S)P(S\to S)+{\alpha }_1(C)P(C\to S)+{\alpha }_1(R)P(R\to S)$$

最后还要乘上“Sunny 天看到打伞”的概率：

$${\alpha }_2(S)=\left[{\alpha }_1(S)P(S\to S)+{\alpha }_1(C)P(C\to S)+{\alpha }_1(R)P(R\to S)\right]\times P(\text{打伞}|S)$$

同理可得：

• 今天是 Cloud 的概率
• 今天是 Rain 的概率

---

Step 3：第三天（t=3）

做法完全一致：

• 从 Day2 的三种天气延伸三条路径
• 加总
• 乘以“不打伞”的概率

得到：

$${\alpha }_3(S),{\alpha }_3(C),{\alpha }_3(R)$$

---

Step 4：最终结果

$$P(O)={\alpha }_3(S)+{\alpha }_3(C)+{\alpha }_3(R)$$

它表示：

从所有可能天气路径（S/C/R）出发，能解释我们看到的观测序列的总概率。

这就是前向算法所有内容。

---

四、核心公式到底在干什么？（最通俗解释）

把重点公式再看一遍：

$${\alpha }_t(i)=\left[\sum _{j=1}^N{\alpha }_{t-1}(j)P(s_i|s_j)\right]\times P(o_t|s_i)$$

每一部分的直觉：

✔ ( $a_{t-1}(j)$)

昨天是状态 j 的概率
（所有可能的昨天）

✔ ($P(s_i|s_j)$)

昨天是 j，今天转移到 i 的概率
（状态转移概率）

✔ 相加（$\Sigma$）

所有“昨天 → 今天 i 的路径”相加
（因为这些路径都可能导致今天是 i）

✔ 最后乘 ($P(o_t|s_i)$)

因为今天我们看到了 “打伞/不打伞”
必须乘上“状态 i 产生该观测的概率”

---

五、用一句废话总结（但你永远不会忘）

“今天是某个状态的概率 =
（昨天各种状态到今天的路径概率相加）
×（今天该状态能解释当前观测的能力）”

这个过程重复 T 天，就能得到整串观测的总概率。