所有题目链接：

https://leetcode.cn/problem-list/V3JZGPzX/https://leetcode.cn/problem-list/V3JZGPzX/

一.递归:

509, 斐波那契数

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        else:
            return self.fib(n-1) + self.fib(n-2)

二.分治:

169， 多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

思路，分治法，通过设置一个递归merge函数。设置初始起点和终点，通过递归调用的方式实现分治

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        # 怎么实现分治
        # 用下标来实现
        def merge(l, r):
            if l == r:
                return nums[l]
            mid = (l + r) // 2
            # 用递归调用的形式完成分治
            left_major = merge(l, mid)
            right_major = merge(mid + 1, r)
            # 如果左右相同，必然是最终答案
            if left_major == right_major:
                return left_major
            # 如果不同，数一数当前区间哪一个多
            left_count = sum(1 for i in range(l, r + 1) if nums[i] == left_major)
            right_count = sum(1 for i in range(l, r + 1) if nums[i] == right_major)

            return left_major if left_count > right_count else right_major
        return merge(0, len(nums) - 1)

240. 搜索二维矩阵

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

分治法：

class Solution:
    def searchMatrix(self, matrix, target):
        m, n = len(matrix), len(matrix[0])

        def helper(top, bottom, left, right):
            if top > bottom or left > right:
                return False

            # 如果目标超出当前矩阵范围，直接剪枝
            if target < matrix[top][left] or target > matrix[bottom][right]:
                return False

            mid_col = (left + right) // 2

            # 在中间列上查找可能的行
            row = top
            while row <= bottom and matrix[row][mid_col] <= target:
                if matrix[row][mid_col] == target:
                    return True
                row += 1

            # 分成两块继续查
            return helper(row, bottom, left, mid_col - 1) or helper(top, row - 1, mid_col + 1, right)

        return helper(0, m - 1, 0, n - 1)

# 利用矩阵有序性进行的贪心式查找方法：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        r, c = 0, n - 1 
        while r < m and c >= 0:
            if matrix[r][c] == target:
                return True
            elif matrix[r][c] > target:
                c -= 1
            else: # matrix[r][c] < target:
                r += 1  

三.单调栈

503， 下一个更大的元素II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

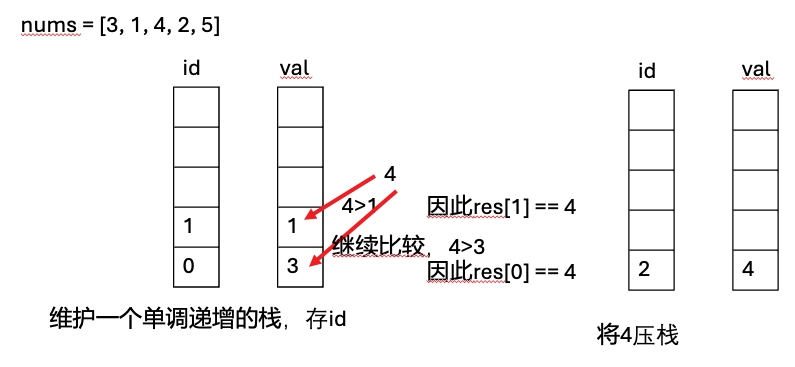
# 单调栈：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        res = [-1]* len(nums)
        stack = []
        for j in range(len(nums)*2):
            while stack and nums[stack[-1]] < nums[j%len(nums)]:
                id = stack.pop()
                res[id] = nums[j%len(nums)]
            if j <len(nums):
                stack.append(j)
        return res

# 暴力解法（Brute Force），并不是单调栈。它的核心思想是：

对每个元素，都重新构造一个从它开始的线性数组，然后从头往后找第一个比它大的数。

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        def linear(nums):
            for id, val in enumerate(nums[1:]):
                if val > nums[0]:
                    return val
            return -1


        record = []
        for i in range(len(nums)):
            new_nums = nums[i:]+nums[:i]
            record.append(linear(new_nums))
        return record

六. 前缀和

560, 和为K的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

子数组是数组中元素的连续非空序列。

思路，把这个看成两个前缀和数组之间的差即可：

在遍历时，同步处理一个prefix的值，通过在x出的prefix和减去k等于之前出现过的prefix的频率，每存在一个这样的历史prefix，就可以满足那个历史prefix到x之间的间隔的和等于k。

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:

        prefix = 0
        count = 0
        freq = {0: 1}

        for x in nums:
            prefix += x

            if prefix - k in freq: # 存在满足要求的prefix 
                count += freq[prefix - k] # 如果 prefix - k 在 freq 中出现 freq[prefix - k] 次（考虑存在负数）

            freq[prefix] = freq.get(prefix, 0) + 1 # prefix - k in freq:

        return count

七. 差分

121，买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        m = prices[0]
        best = 0
        for i in range(1,len(prices)):
            if prices[i] < m:
                m =  prices[i]
            best = max(best, prices[i]-m)
        return best

九. 字符串

20，有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

思路：通过建立一个栈即可解决，左括号出现时压栈，右括号出现时出栈。

出现右括号时：判断栈顶的左括号是否和右括号匹配

遍历完后要判断stack是否为空

class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        pairs = {')': '(', ']': '[', '}': '{'}    
        for ch in s:
            if ch in "([{":
                stack.append(ch) # 压栈
            else:
                if not stack or stack[-1] != pairs[ch]:
                    return False
                else:
                    stack.pop()
        return len(stack) == 0

十三. 动态规划

62.不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

思路：使用动态规划法

建立一个矩阵，初始化为1，根据动态规划公式遍历得到最终矩阵即可

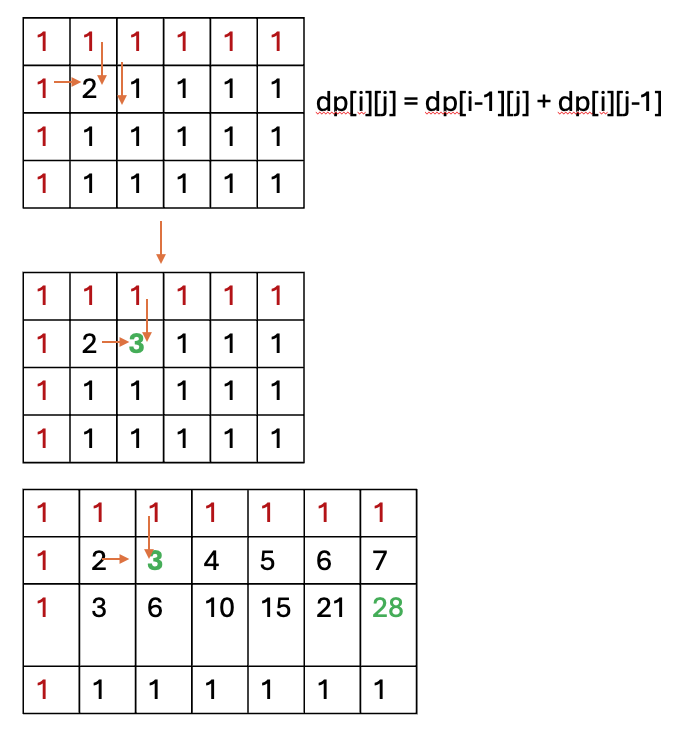
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        map = [[1]*n for i in range(m)]


        for i in range(1,m):
            for j in range(1,n):
                map[i][j] = map[i-1][j]+ map[i][j-1]
        return map[m-1][n-1]

0-1背包问题

有 n 件物品，每件物品有：

• 重量 weight[i]

• 价值 value[i]

你有一个容量为 W 的背包。每件物品 只能选 0 次或 1 次。问在不超过背包容量的前提下，能获得的最大价值是多少。

思路：

物品数量是单调增加的。

对于第i个物品，其解来自于之前的两种情况

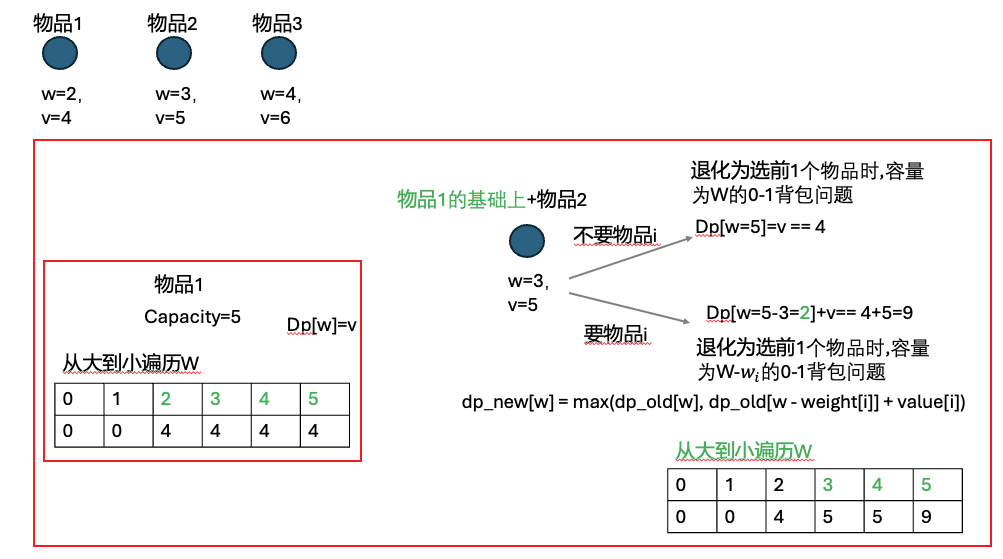
需要注意的是：

1，外层循环是物体数，这个动态规划是从一个物体开始，不断增加物体的最佳子结构问题

2，每个外循环中，需要将背包容量再逐步减小，解决当前物体个数时，背包容量从大到小的各个子问题

def knapsack(weights, values, W):
    n = len(weights)
    dp = [0] * (W + 1)

    for i in range(n): # 物品数量不断增加，子问题不断变大
        w = weights[i]
        v = values[i]
        # 容量从大到小遍历
        for capacity in range(W, w - 1, -1):
            dp[capacity] = max(dp[capacity], dp[capacity - w] + v)

    return dp[W]

max under limit 问题

给定一些数，从中选择若干，使它们的和 不超过某个限制 limit，并且 尽量大。

它本质上就是 0-1 背包问题的简化版（只有重量，没有价值），常见于：

• 找到不超过 limit 的最大子集和

• 文件打包

• 预算规划

• 时间限制内最多安排任务

示例：

nums = [3, 5, 7], limit = 10
答案 = 10  (3 + 7)

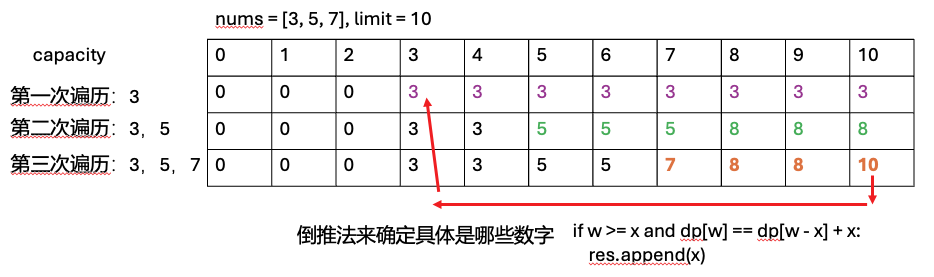
def max_under_limit_with_choice(nums, limit):
    dp = [0] * (limit + 1)

    # 构建 dp
    for x in nums:
        for w in range(limit, x - 1, -1):
            dp[w] = max(dp[w], dp[w - x] + x)

    # 回溯找到具体选了哪些数字
    res = []
    w = limit

    for x in reversed(nums):               # 从后往前检查
        if w >= x and dp[w] == dp[w - x] + x:
            res.append(x)
            w -= x

    return dp[limit], res[::-1]

十四. 贪心算法

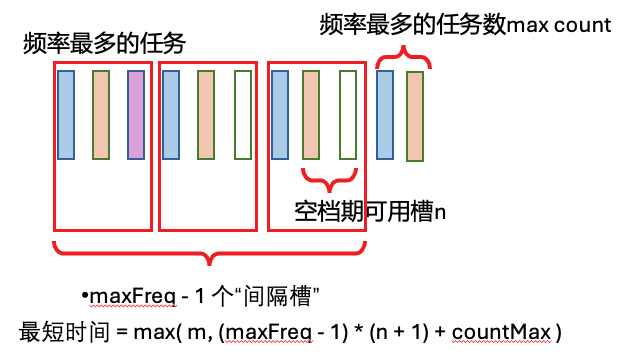
621，任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表，用字母 A 到 Z 表示，以及一个冷却时间 n。每个周期或时间间隔允许完成一项任务。任务可以按任何顺序完成，但有一个限制：两个 相同种类 的任务之间必须有长度为 n 的冷却时间。

返回完成所有任务所需要的 最短时间间隔 。

class Solution:
    def leastInterval(self, tasks: List[str], n: int) -> int:
        freq = {}
        for t in tasks:
            freq[t] = freq.get(t, 0) + 1

        maxFreq = max(freq.values())
        countMax = sum(1 for x in freq.values() if x == maxFreq)

        part_count = maxFreq - 1
        part_len = n + 1

        min_time = part_count * part_len + countMax # 有idle时，最小的时间

        return max(min_time, len(tasks)) # 即使没有任何 idle，也需要执行 len(tasks) 次操作

十一. BFS（广度优先搜索）

139，单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

deque库

from collections import deque
q = deque()              # 空队列
q = deque([1, 2, 3])     # 带初始元素
q.append(x)
x = q.popleft()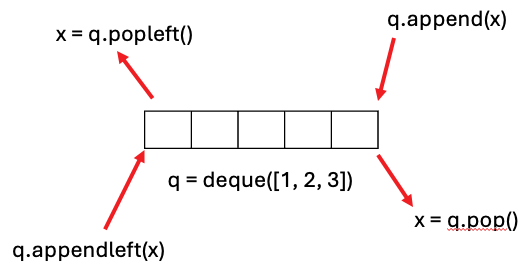

为什么用宽度优先搜索：因为可能存在单词不同的拼法

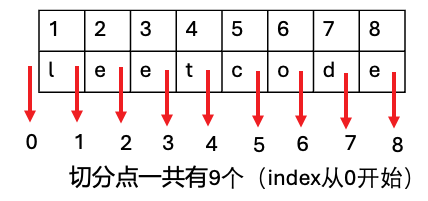
切分点的问题：

从index==0开始切分。到end时切分完，因此切分点的id数刚好等于len(s)

set的操作：

# 如何创建 set
s = set()
s = {1, 2, 3}
s = set([1, 2, 3])

# 添加元素
s.add(x)

# 删除元素
s.remove(x)      # x 不存在会报错
s.discard(x)     # x 不存在也不会报错

# 判断是否存在（O(1)）
if x in s:

# 集合大小
len(s)

#清空
s.clear()

代码实现：

from collections import deque
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        setsize = len(wordDict)
        wordSet = set(wordDict) # 要set化才行
        wordlen = len(s)
        q = deque([0])
        visited = set([0])

        while q:
            start = q.popleft()
            if start == len(s):
                return True
            for end in range(start+1, wordlen+1):
                if end not in visited and s[start:end] in wordDict:
                    q.append(end)
                    visited.add(end)
        return False