前言

Hi，我是GISerLiu🙂, 这篇文章是参加2025年5月datawhale学习赛的打卡文章！💡 本文详细讲解了如何使用PyPOTS预处理自定义时序数据集并进行缺失值插补。

在医疗、金融、物联网等领域，时序数据常常面临缺失值问题，这严重影响下游分析任务的准确性。本文将基于合成eICU数据集，系统介绍自定义时序数据预处理流程和SAITS模型的缺失值插补原理，以解决实际应用中的数据质量问题。

---

一、时序数据缺失问题与插补的重要性

时间序列数据在实际应用中普遍存在缺失值问题，这些缺失可能源于多种因素：传感器故障、人为跳过某些测量、数据传输错误等。处理这些缺失值至关重要，原因有以下几点：

1. 缺失值带来的挑战

• 数据分析视角：缺失值使许多统计方法和机器学习算法无法直接应用，因为大多数算法都假设输入数据是完整的。这意味着我们必须先解决缺失值问题，才能进行后续分析。

• 信息损失：缺失数据意味着信息的丢失，尤其是在时序数据中，某个时间点的缺失可能打断时间序列的连续性，导致趋势和模式识别变得困难。

• 统计偏差：如果简单地删除或忽略缺失数据，可能会引入严重的统计偏差，特别是当缺失并非完全随机（MCAR）时。

2. 插补方法的发展

时序数据缺失值插补方法大致可分为以下几类：

深度学习的优势：与传统方法相比，深度学习方法能够：

• 捕捉时序数据中的复杂非线性关系
• 同时考虑特征间的相互依赖关系
• 更好地处理长序列和多变量时间序列
• 提供端到端的解决方案

3. 医疗时序数据的特殊性

医疗时序数据（如eICU数据集）具有一些独特特点：

• 不规则采样：患者数据采集通常是不规则的，取决于医生判断和病情变化
• 多变量相关性：不同生理指标之间存在复杂的相互关系
• 缺失不随机：缺失往往与患者状态相关，属于非随机缺失（MNAR）
• 缺失率高：某些指标可能有高达30%-70%的缺失率
• 生命特征变化快：数据可能在短时间内快速变化

这些特点使得医疗时序数据的插补特别具有挑战性，需要使用专门针对时序特性设计的插补方法。

4. Wang等人的时序插补综述

Wang等人在2025年IJCAI发表的综述《Deep Learning for Multivariate Time Series Imputation: A Survey》全面分析了深度学习在时序插补领域的进展，该文归纳了几个关键洞见：

1. 架构演变：从RNN到Transformer，再到专用的混合架构
2. 插补策略：从简单填充到生成式模型的发展
3. 损失函数设计：多目标优化的重要性
4. 评估指标：不同场景下的适用度量
5. 未来研究方向：不确定性量化、因果推断和预训练等

现在，让我们基于这些理论基础，探索PyPOTS如何帮助我们解决实际问题。

---

二、自定义时序数据预处理流程

在开始使用PyPOTS进行插补前，我们需要将自定义的时序数据转换为PyPOTS能够处理的格式。以下是详细的预处理流程：

1. 数据格式要求

PyPOTS要求输入数据为3D张量，格式为(n_samples, n_steps, n_features)：

• n_samples：样本数量（如患者数量）
• n_steps：时间步长（如每个患者的观测次数）
• n_features：特征维度（如生理指标的数量）

缺失值用np.nan表示，模型将自动识别这些位置并进行插补。

2. 预处理步骤

我们的预处理流程如下：

下面我们将通过代码演示整个过程：

3. 代码实现

① 导入必要的库

import pypots
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from benchpots.utils.missingness import create_missingness  # 生成人工缺失值
from pypots.data.saving import pickle_dump

② 数据加载与理解

首先加载我们的合成eICU数据集：

# 加载数据
df = pd.read_csv('attachments/synthetic_eicu.csv')
print("原始数据集形状:", df.shape)
print("数据集列名:", df.columns.tolist())
df.head()

这里我们应当看到类似如下输出：

③ 样本切分与对齐

医疗时序数据中，不同患者的观测次数通常不同，我们需要将它们对齐到相同长度：

# 确保时间步长的一致性
max_length = 48  # 假设每个患者最多有48小时的记录

def pad_truncate(df):
    """填充或截断每个样本到统一长度"""
    if len(df) > max_length:
        # 如果超过最大长度，则截断前max_length行
        return df.iloc[:max_length]
    else:
        # 如果少于最大长度，则用NaN填充
        padding = pd.DataFrame(
            index=range(max_length - len(df)),
            columns=df.columns
        )
        if not padding.empty:
            return pd.concat([df, padding])
        else:
            return df

# 对每个患者的时间序列进行填充或截断
new_df = df.groupby('sample_id').apply(pad_truncate).reset_index(drop=True)
print(f"对齐后数据形状: {new_df.shape}")

④ 数据拆分

将数据集分为训练集、验证集和测试集：

# 获取唯一的样本ID
unique_sample_ids = new_df['sample_id'].unique()
print(f"样本数量: {len(unique_sample_ids)}")

# 按样本ID进行分割（确保同一患者的数据不会同时出现在训练和测试集）
train_ids, temp_ids = train_test_split(unique_sample_ids, test_size=0.2, random_state=42)
val_ids, test_ids = train_test_split(temp_ids, test_size=0.5, random_state=42)

# 根据样本ID筛选数据
train_df = new_df[new_df['sample_id'].isin(train_ids)]
val_df = new_df[new_df['sample_id'].isin(val_ids)]
test_df = new_df[new_df['sample_id'].isin(test_ids)]

print(f"训练集形状: {train_df.shape}")
print(f"验证集形状: {val_df.shape}")
print(f"测试集形状: {test_df.shape}")

# 拆分特征和标签
def separate_features_labels(df, feature_cols, label_col='label'):
    """将数据拆分为特征和标签"""
    # 将特征重塑为3D张量: (样本数, 时间步, 特征数)
    X = df[feature_cols].values.reshape(-1, max_length, len(feature_cols))
    
    # 获取每个样本的标签（假设每个样本有一个标签）
    unique_ids = df['sample_id'].unique()
    y = df.groupby('sample_id')[label_col].first().loc[unique_ids].values
    
    return X, y

# 选择特征列（排除ID、标签和时间戳）
feature_columns = [col for col in df.columns if col not in ['sample_id', 'label', 'timestamp']]
print(f"特征数量: {len(feature_columns)}")
print(f"特征列表: {feature_columns}")

# 构建特征和标签
train_X, train_y = separate_features_labels(train_df.copy(), feature_columns)
val_X, val_y = separate_features_labels(val_df.copy(), feature_columns)
test_X, test_y = separate_features_labels(test_df.copy(), feature_columns)

print(f"训练特征形状: {train_X.shape}, 训练标签形状: {train_y.shape}")
print(f"验证特征形状: {val_X.shape}, 验证标签形状: {val_y.shape}")
print(f"测试特征形状: {test_X.shape}, 测试标签形状: {test_y.shape}")

⑤ 数据标准化

对特征进行标准化处理：

# 创建标准化器
scaler = StandardScaler()

# 标准化前需要先将3D张量展平为2D
train_X = scaler.fit_transform(train_X.reshape(-1, train_X.shape[-1])).reshape(train_X.shape)
val_X = scaler.transform(val_X.reshape(-1, val_X.shape[-1])).reshape(val_X.shape)
test_X = scaler.transform(test_X.reshape(-1, test_X.shape[-1])).reshape(test_X.shape)

print("标准化后的数据范围示例 (训练集前5个样本第1个特征):")
print(train_X[:5, 0, 0])

⑥ 组织处理后的数据集

# 整合处理后的数据集为字典格式
processed_dataset = {
    # 基本信息
    "n_classes": len(np.unique(train_y)),
    "n_steps": train_X.shape[1],
    "n_features": train_X.shape[2],
    "scaler": scaler,
    # 训练集
    "train_X": train_X,
    "train_y": train_y.flatten(),
    # 验证集
    "val_X": val_X,
    "val_y": val_y.flatten(),
    # 测试集
    "test_X": test_X,
    "test_y": test_y.flatten(),
}

print(f"处理完成的数据集包含 {processed_dataset['n_classes']} 个类别")
print(f"每个样本有 {processed_dataset['n_steps']} 个时间步")
print(f"每个时间步有 {processed_dataset['n_features']} 个特征")

⑦ 创建人工缺失值

为了演示插补效果，我们在原始数据上创建人工缺失：

# 保存原始数据作为真实值(ground truth)用于评估
train_X_ori = train_X.copy()
val_X_ori = val_X.copy()
test_X_ori = test_X.copy()

# 设置缺失率
rate = 0.3  # 30%缺失率
print(f"创建 {rate*100}% 的人工缺失值")

# 在各数据集上创建随机点状缺失
train_X = create_missingness(train_X, rate, 'point')
val_X = create_missingness(val_X, rate, 'point')
test_X = create_missingness(test_X, rate, 'point')

# 计算实际缺失率
train_missing_rate = np.isnan(train_X).sum() / train_X.size
val_missing_rate = np.isnan(val_X).sum() / val_X.size
test_missing_rate = np.isnan(test_X).sum() / test_X.size

print(f"训练集实际缺失率: {train_missing_rate:.4f}")
print(f"验证集实际缺失率: {val_missing_rate:.4f}")
print(f"测试集实际缺失率: {test_missing_rate:.4f}")

# 更新数据集字典
processed_dataset["train_X"] = train_X
processed_dataset["val_X"] = val_X
processed_dataset["test_X"] = test_X

processed_dataset['train_X_ori'] = train_X_ori
processed_dataset['val_X_ori'] = val_X_ori
processed_dataset['test_X_ori'] = test_X_ori

# 保存处理后的数据集
pickle_dump(processed_dataset, "result_saving/processed_synthetic_eicu.pkl")
print("已保存预处理后的数据集到 result_saving/processed_synthetic_eicu.pkl")

OK,这里我们已经训练好了模型！🙂👌

⑧ 准备用于插补的数据

开始准备插补要用的数据：

# 计算指示掩码，标记人工缺失的位置（将用于评估）
train_X_indicating_mask = np.isnan(train_X_ori) ^ np.isnan(train_X)
val_X_indicating_mask = np.isnan(val_X_ori) ^ np.isnan(val_X)
test_X_indicating_mask = np.isnan(test_X_ori) ^ np.isnan(test_X)

# 组装训练集
dataset_for_training = {
    "X": processed_dataset['train_X'],
    'X_ori': processed_dataset['train_X_ori'],
}

# 组装验证集
dataset_for_validating = {
    "X": processed_dataset['val_X'],
    "X_ori": processed_dataset['val_X_ori'],
}

# 组装测试集
dataset_for_testing = {
    "X": processed_dataset['test_X'],
    "X_ori": processed_dataset['test_X_ori'],
}

# 度量函数不接受NaN输入，因此用0填充NaN（仅用于评估）
test_X_ori = np.nan_to_num(processed_dataset['test_X_ori'])

print("已准备好用于插补的数据集")
print("训练集：\n",dataset_for_training)
print("验证集：\n",dataset_for_validating)
print("测试集：\n",dataset_for_testing)

通过以上步骤，我们已经完成了自定义时序数据的预处理，现在我们将其转换为PyPOTS能够处理的格式。然后使用SAITS模型对缺失值进行插补。

三、SAITS模型原理与时序插补实现

SAITS (Self-Attention-based Imputation for Time Series) 是一种基于自注意力机制的时序数据插补模型，由Yi Ding等人于2022年提出。它融合了Transformer架构的优势和时序数据特有的处理机制，是目前最先进的深度学习时序插补方法之一。

1. SAITS模型架构

SAITS模型主要由以下组件构成：

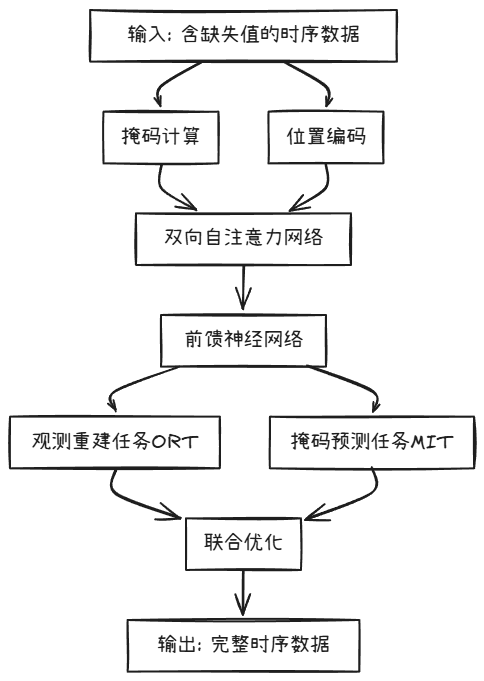
核心特点：

1. 双重任务学习：
   • 观测重建任务 (ORT)：学习重建已知观测值
   • 掩码预测任务 (MIT)：专注于预测缺失值
2. 自注意力机制：能够捕捉任意时间步之间的长距离依赖关系，适合不规则采样的医疗数据
3. 无需循环结构：与RNN/LSTM不同，允许并行计算，大幅提高训练效率
4. 位置敏感：通过位置编码保留时序信息

2. 模型数学原理

SAITS的核心数学公式包括：

自注意力计算：
$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

其中：

• $Q,K,V$ 是查询、键和值矩阵
• $d_k$ 是键的维度

损失函数：
$$\mathcal{L}={\lambda }_{ORT}\cdot {\mathcal{L}}_{ORT}+{\lambda }_{MIT}\cdot {\mathcal{L}}_{MIT}$$

其中：

• ${\mathcal{L}}_{ORT}$ 是观测重建任务的损失
• ${\mathcal{L}}_{MIT}$ 是掩码预测任务的损失
• ${\lambda }_{ORT},{\lambda }_{MIT}$ 是权衡两个任务的权重

这种设计使SAITS能够同时关注已知数据的重建和缺失数据的预测，达到更好的插补效果。

3. PyPOTS中的SAITS实现

PyPOTS框架提供了SAITS模型的高效实现，使用非常直观：

from pypots.imputation import SAITS
from pypots.nn.functional import calc_mae
from pypots.optim import Adam

# 设置运行设备
DEVICE = 'cpu'  # 如有GPU可设为'cuda'

# 创建SAITS模型
saits = SAITS(
    n_steps=processed_dataset['n_steps'],      # 时间步数
    n_features=processed_dataset['n_features'],  # 特征数
    n_layers=1,        # Transformer编码器层数
    d_model=256,       # 模型维度
    d_ffn=128,         # 前馈网络维度
    n_heads=4,         # 多头注意力的头数
    d_k=64,            # 键维度
    d_v=64,            # 值维度
    dropout=0.1,       # Dropout比率
    ORT_weight=1,      # 观测重建任务权重
    MIT_weight=1,      # 掩码预测任务权重
    batch_size=32,     # 批处理大小
    epochs=20,         # 训练轮数
    patience=3,        # 早停耐心值
    optimizer=Adam(lr=1e-3),  # 优化器
    num_workers=0,     # 数据加载器工作进程数
    device=DEVICE,     # 运行设备
    saving_path="result_saving/imputation/saits",  # 保存路径
    model_saving_strategy="best",  # 模型保存策略
)

# 训练模型
print("开始训练SAITS模型...")
saits.fit(train_set=dataset_for_training, val_set=dataset_for_validating)
print("模型训练完成!")

# 在测试集上进行插补
print("开始在测试集上插补...")
test_set_imputation = saits.impute(dataset_for_testing)

# 计算平均绝对误差评估插补质量
testing_mae = calc_mae(
    test_set_imputation,
    test_X_ori,
    test_X_indicating_mask,
)
print(f"测试集平均绝对误差 (MAE): {testing_mae:.4f}")

这里需要注意以下关键参数：

• n_layers, d_model, n_heads：控制Transformer架构的复杂度
• ORT_weight, MIT_weight：控制两个任务的相对重要性
• patience：控制早停机制，防止过拟合
• model_saving_strategy：决定保存最佳模型的策略

开始模型训练！

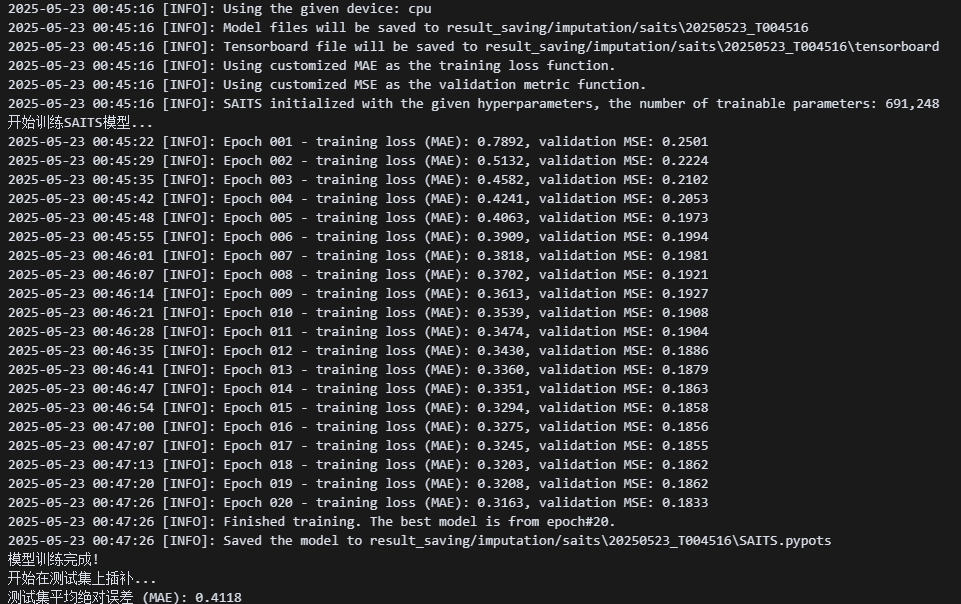
这里训练了20轮，但是从10轮足够使用了；各位根据自己设备情况选择；🤔

4. 模型训练过程分析

SAITS模型的训练过程具有以下特点：

1. 双任务联合优化：同时优化ORT和MIT任务，使模型既能准确重建已知值，也能精确预测缺失值
2. 前向传播：
   • 计算自注意力权重
   • 进行特征转换
   • 分别计算两个任务的输出
3. 反向传播：
   • 计算组合损失
   • 更新所有参数
4. 验证评估：
   • 在验证集上计算插补误差
   • 根据早停策略决定是否继续训练
5. 测试推断：
   • 使用训练好的模型对测试集进行插补
   • 计算插补误差进行评估

具体细节这里我们已经在上一篇文章中有详细说明，这里不再做更多赘述！

5. 对完整训练集和验证集进行插补

完成测试集评估后，我们可以对所有数据集进行插补：

# 对所有数据集进行插补
print("开始对所有数据集进行插补...")
train_set_imputation = saits.impute(dataset_for_training)
val_set_imputation = saits.impute(dataset_for_validating)

# 更新处理后的数据集
processed_dataset['train_X'] = train_set_imputation
processed_dataset['val_X'] = val_set_imputation
processed_dataset['test_X'] = test_set_imputation

# 保存插补后的数据集
pickle_dump(processed_dataset, "result_saving/imputed_synthetic_eicu.pkl")
print("已保存插补后的数据集到 result_saving/imputed_synthetic_eicu.pkl")

通过这一步，我们获得了完整的插补后数据集，可以用于后续的分析和建模任务。

---

四、插补结果重构与应用

完成数据插补后，我们通常需要将3D张量格式的数据转换回原始的表格形式，以便进行后续分析或可视化。下面我们展示如何完成这一过程：

1. 从3D张量格式重构为CSV表格数据

我们设计一个函数，将3D张量转换为DataFrame格式：

def convert_to_dataframe(X, labels, sample_ids, scaler, inverse_norm=False, n_steps=48):
    """
    将3D NumPy数组转换为DataFrame，包含sample_id、timestamp和特征
    
    参数:
    - X: 形状为(n_samples, n_steps, n_features)的3D NumPy数组
    - labels: 形状为(n_samples,)的1D NumPy数组，表示每个样本的标签
    - sample_ids: 对应于每个样本的样本ID
    - scaler: 用于标准化的缩放器(StandardScaler/MinMaxScaler)
    - inverse_norm: 是否进行反标准化处理，默认为False
    - n_steps: 时间步数，默认为48
    
    返回:
    - 包含sample_id、timestamp、特征和标签的DataFrame
    """
    # 获取数据维度
    n_samples, _, n_features = X.shape
    
    # 验证维度匹配
    assert len(feature_columns) == n_features, "X中的特征数与feature_columns不匹配"
    assert len(labels) == n_samples, "标签数量与样本数量不匹配"
    assert len(sample_ids) == n_samples, "样本ID数量与样本数量不匹配"
    
    # 提取每个样本的最后一个时间步记录
    # 这里我们选择最后一个时间步，也可以选择其他策略
    X_last = X[:, -1, :]  # 形状: (n_samples, n_features)
    
    # 反标准化处理（如需要）
    if inverse_norm:
        X_original = scaler.inverse_transform(X_last)
    else:
        X_original = X_last
    
    # 创建DataFrame
    df = pd.DataFrame(X_original, columns=feature_columns)
    df['sample_id'] = sample_ids
    df['timestamp'] = n_steps - 1  # 最后一个时间步（如果从0开始索引，则为47）
    df['label'] = labels
    
    # 重排列顺序: sample_id, timestamp, 特征, label
    df = df[['sample_id', 'timestamp'] + feature_columns + ['label']]
    
    return df

# 使用函数转换插补后的数据
df_train_imputed = convert_to_dataframe(train_set_imputation, train_y, train_ids, scaler)
df_val_imputed = convert_to_dataframe(val_set_imputation, val_y, val_ids, scaler)
df_test_imputed = convert_to_dataframe(test_set_imputation, test_y, test_ids, scaler)

# 检查数据集形状
print("插补后数据集形状:")
print(f"训练集: {df_train_imputed.shape}")
print(f"验证集: {df_val_imputed.shape}")
print(f"测试集: {df_test_imputed.shape}")

# 查看训练集前几行
print("\n插补后训练集示例:")
print(df_train_imputed.head())

# 保存转换后的数据集为CSV文件
df_train_imputed.to_csv('result_saving/train_imputed.csv', index=False)
df_val_imputed.to_csv('result_saving/val_imputed.csv', index=False)
df_test_imputed.to_csv('result_saving/test_imputed.csv', index=False)
print("\n已保存插补后的数据集为CSV文件")

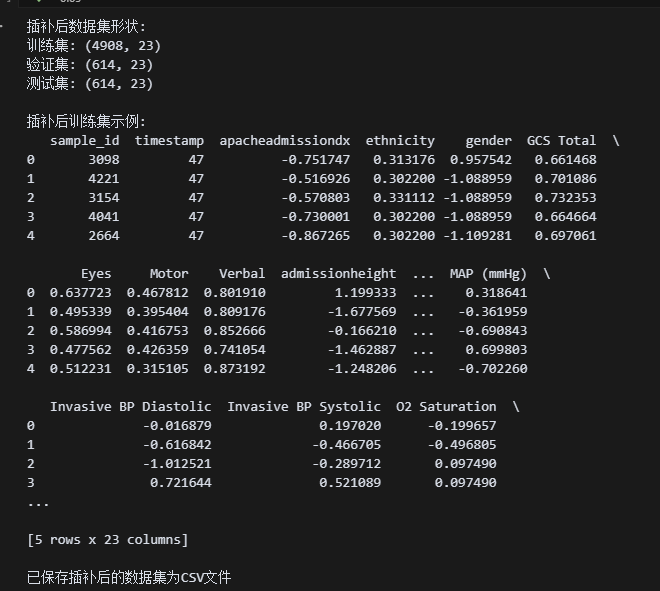
可以看到，数据已经转化完毕！

2. 插补效果评估

为了更全面地评估插补效果，我们可以计算不同指标并可视化结果：

import matplotlib.pyplot as plt
from pypots.nn.functional import calc_mae, calc_mse, calc_mre
import seaborn as sns

# 计算不同评估指标
mae = calc_mae(test_set_imputation, test_X_ori, test_X_indicating_mask)
mse = calc_mse(test_set_imputation, test_X_ori, test_X_indicating_mask)
mre = calc_mre(test_set_imputation, test_X_ori, test_X_indicating_mask)

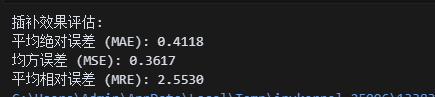
print("插补效果评估:")
print(f"平均绝对误差 (MAE): {mae:.4f}")
print(f"均方误差 (MSE): {mse:.4f}")
print(f"平均相对误差 (MRE): {mre:.4f}")

# 可视化原始值与插补值对比
def visualize_imputation(original, imputed, mask, feature_idx=0, sample_idx=0):
    """可视化单个样本的原始值与插补值"""
    plt.figure(figsize=(10, 6))
    
    # 提取数据
    time_steps = np.arange(original.shape[1])
    orig_values = original[sample_idx, :, feature_idx]
    imp_values = imputed[sample_idx, :, feature_idx]
    missing_mask = mask[sample_idx, :, feature_idx]
    
    # 绘制原始值
    plt.plot(time_steps, orig_values, 'b-', label='原始值')
    
    # 绘制缺失位置的插补值
    plt.plot(time_steps[missing_mask], imp_values[missing_mask], 'ro', label='插补值')
    
    # 添加图例和标签
    plt.legend()
    plt.title(f'特征 {feature_columns[feature_idx]} 的原始值与插补值对比')
    plt.xlabel('时间步')
    plt.ylabel('标准化值')
    plt.grid(True)
    
    plt.tight_layout()
    plt.savefig(f'result_saving/imputation_feature{feature_idx}_sample{sample_idx}.png')
    plt.close()

# 为前3个特征和前2个样本生成可视化
for feature_idx in range(min(3, test_X_ori.shape[2])):
    for sample_idx in range(min(2, test_X_ori.shape[0])):
        visualize_imputation(test_X_ori, test_set_imputation, test_X_indicating_mask, feature_idx, sample_idx)

print("已生成插补效果可视化图像，保存在result_saving目录")

3. 插补结果的应用场景

成功完成数据插补后，我们便可以在多种下游任务中应用这些完整数据：

1. 分类任务：预测患者的疾病风险、ICU转入或死亡风险
2. 回归任务：预测患者的住院时长、所需药物剂量
3. 时序预测：预测未来生命体征变化趋势
4. 异常检测：识别生理指标的异常模式
5. 聚类分析：发现患者亚群或疾病亚型

这里以分类任务为例，可以使用插补后的数据训练一个简单随机森林模型：

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report

# 使用插补后的最后一个时间步数据进行分类
X_train = df_train_imputed[feature_columns].values
X_val = df_val_imputed[feature_columns].values
X_test = df_test_imputed[feature_columns].values

y_train = df_train_imputed['label'].values
y_val = df_val_imputed['label'].values
y_test = df_test_imputed['label'].values

# 训练随机森林分类器
print("训练随机森林分类器...")
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

# 预测和评估
y_pred = rf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"测试集准确率: {accuracy:.4f}")
print("\n分类报告:")
print(classification_report(y_test, y_pred))

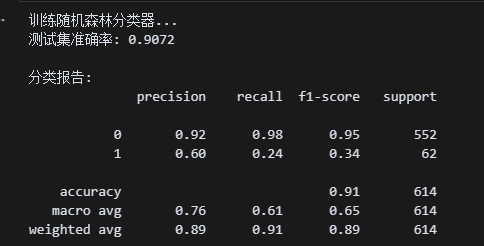
效果还可以哦！🙂🎉，可以拿来预测了！

---

五、PyPOTS深度学习插补的优势与局限

通过上面的案例演示，作者通过和AI沟通总结以下PyPOTS框架和深度学习插补方法的优势和局限性：

1. PyPOTS框架的优势

🚀 简化的工作流程：PyPOTS提供了从数据预处理到模型训练、评估的完整工具链，大大减少了代码量和开发时间。

🔍 多种先进模型：框架集成了多种最先进的深度学习插补模型，包括SAITS、BRITS等。

🛠️ 灵活的配置：提供丰富的参数选项，可以针对不同数据集特点进行调优。

📊 全面的评估指标：内置多种评估指标，方便比较不同模型的性能。

💾 高效的数据处理：优化的数据加载和批处理机制，提高训练效率。

2. SAITS模型的优势

✅ 处理复杂依赖关系：自注意力机制能捕捉时序数据中的长距离和跨特征依赖关系。

✅ 适应不规则采样：适合处理医疗时序数据常见的不规则采样问题。

✅ 并行计算：无需循环结构，可以并行计算，大幅提高效率。

✅ 双任务学习：ORT和MIT两个任务的联合优化提高了插补的准确性。

3. 方法的局限性

⚠️ 计算资源需求：深度学习模型训练需要较高的计算资源，特别是处理大规模数据时。

⚠️ 超参数调优：模型性能对超参数敏感，可能需要大量实验来确定最佳配置。

⚠️ 可解释性不足：与简单统计方法相比，深度学习模型的插补结果难以直观解释。

⚠️ 数据量要求：需要足够大的训练集才能发挥深度学习的优势。

4. 适用场景建议

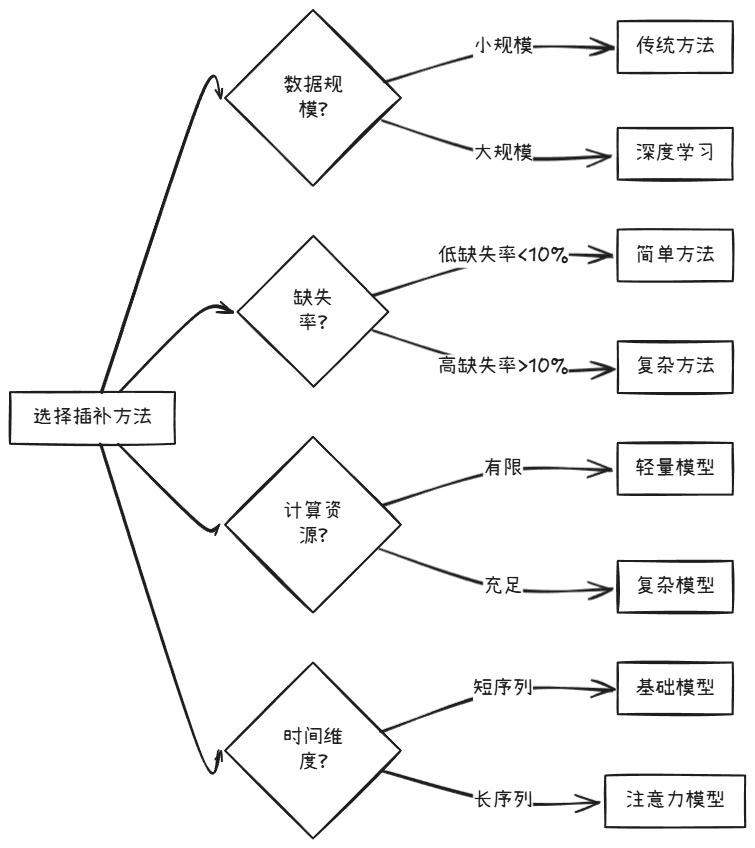
推荐策略：

• 如果缺失率低且数据简单：可以使用均值/中位数插补等简单方法
• 如果缺失率中等且结构有规律：可以使用PyPOTS中的BRITS模型
• 如果缺失率高且关系复杂：建议使用SAITS模型
• 如果序列特别长：优先考虑基于Transformer的模型

5. 与Wang等人综述的关联

Wang等人在2025年的综述中提出了几个时序插补的研究方向，与我们的实践紧密相关：

1. 因果插补：区分不同缺失机制（MCAR/MAR/MNAR）的插补策略
2. 不确定性量化：提供插补值的置信区间，而非单点估计
3. 联合任务学习：将插补与下游任务联合优化
4. 可解释插补：提高深度学习插补模型的可解释性

PyPOTS框架正在这些方向上不断发展，未来版本可能会增加更多这些前沿技术的实现。

---

总结

作者在本文中以合成的eICU数据集为例，详细演示了自定义时序数据的预处理流程和基于PyPOTS的SAITS模型进行插补的完整过程。主要有：

1. 数据预处理：加载原始数据，对齐时间步长，划分数据集，标准化特征，创建人工缺失
2. 模型训练：配置和训练SAITS模型，实现高质量的缺失值插补
3. 结果应用：将插补后的数据转换回原始格式，用于下游任务

通过这个过程，各位读者不仅解决了时序数据中的缺失值问题，还了解了深度学习插补方法的工作原理和应用策略。PyPOTS框架的简洁API和强大功能，使得复杂的时序插补任务变得简单易行。

在实际应用中，我们应根据数据特点、缺失模式和可用资源，选择合适的插补策略。对于医疗、金融等高价值时序数据，深度学习插补方法通常能提供更准确的结果；

好的，今天的学习就到这里了！🙂

参考资料

1. Deep Learning for Multivariate Time Series Imputation: A Survey. IJCAI 2025.
2. PyPOTS: 深度学习时序插补的Python工具箱
3. SAITS: Self-Attention-based Imputation for Time Series
4. 作者算法专栏

---

如果觉得我的文章对您有帮助，三连+关注便是对我创作的最大鼓励！或者一个star🌟也可以😂.