目录

什么是RNN？

PyTorch 是如何构建和训练神经网络的？

1.网络层（Layers）：

2.损失函数（Loss Functions）：

3.优化器（Optimizers）：

4.训练过程：

（1）数据处理与加载：

（2）线性回归：

（3）定义损失函数与优化器：

（4）训练模型：

使用RNN构建人名国家预测器

1.数据处理与加载：

2.构建RNN模型：

为什么要定义线性层linear？

logit是什么？

为什么要在加一个softmax呢？

为什么要加入x.unsqueeze(0)？

3.使用RNN训练模型：

4.基于训练好的模型构造预测函数：

5.整个训练流程维度变化分析：

什么是RNN？

RNN 是循环神经网络（Recurrent Neural Network），普通神经网络（如全连接层）一次只处理一组输入，无法记忆上下文。但很多任务是序列数据（时间有关），比如：

  • 一句话的文字序列

  • 一段语音的声音波形

  • 一组股票的时间价格序列

这时就需要 RNN。RNN 是一类神经网络架构，专门用于处理序列数据，能够捕捉时间序列或有序数据的动态信息，能够处理序列数据，如文本、时间序列或音频，其关键特性是其能够保持隐状态（hidden state），使得网络能够记住先前时间步的信息，这对于处理序列数据至关重要。

在传统的前馈神经网络（Feedforward Neural Network）中，数据是从输入层流向输出层的，而在 RNN 中，数据不仅沿着网络层级流动，还会在每个时间步骤上传播到当前的隐层状态，从而将之前的信息传递到下一个时间步骤。

隐状态（Hidden State）： RNN 通过隐状态来记住序列中的信息。隐状态是通过上一时间步的隐状态和当前输入共同计算得到的。

循环单元的结构如下：

  • 输入（xt）：在时间步 t 的输入向量。
  • 隐藏状态（ht）​：在时间步 t 的隐藏状态向量，用于存储之前时间步的信息。
  • 输出（yt​）：在时间步 t 的输出向量（可选，取决于具体任务）。

下图是 N vs M（seq2seq架构），输入和输出不等长，主要用于文本翻译任务等：

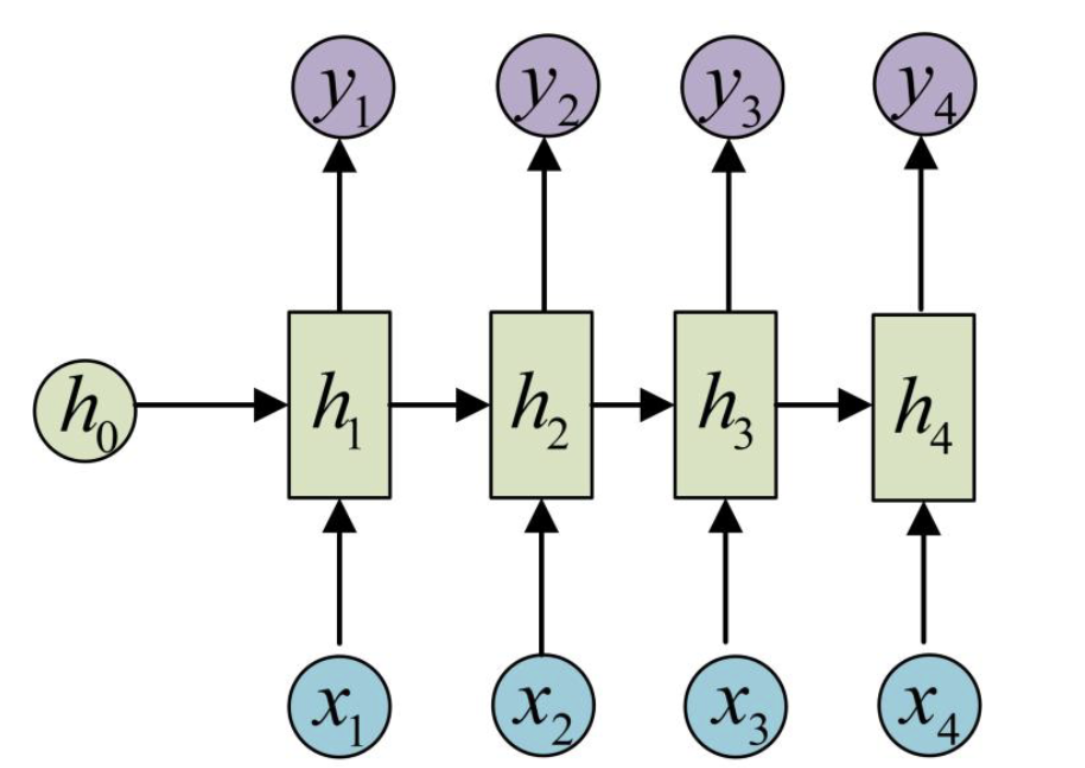
根据上图，我们可以分析出 RNN 在每一个时间步（time step）上都有相同的结构单元（RNN Cell），这些单元会共享权重。

每个单元接收当前时刻输入 xt 和上一时刻的隐藏状态 ht−1，并输出当前隐藏状态 ht 和当前输出 yt。用一个“时间展开（unrolled in time）”的视图来理解：

时间步1        时间步2        时间步3
 t=1            t=2            t=3
 ┌──────┐      ┌──────┐      ┌──────┐
 │x₁──▶│      │x₂──▶│      │x₃──▶│
 │      │      │      │      │      │
 │ h₀──▶│────▶│h₁──▶│────▶│h₂──▶│
 │      │      │      │      │      │
 │      ▼      │      ▼      │      ▼
 │     y₁      │     y₂      │     y₃
 └──────┘      └──────┘      └──────┘

每个时刻的 RNN 单元会将隐藏状态传递到下一个时刻，形成“循环连接”，这也是 “Recurrent” 的来源。

PyTorch 是如何构建和训练神经网络的？

在使用 PyTorch 训练模型时，它之所以强大，是因为 torch.nn 模块提供了构建神经网络所需的一切工具，包括：

1.网络层（Layers）：

网络层就是神经网络中的“变换模块”，输入数据 → 层 → 输出数据，每个层都会执行某种数学运算，例如：线性变换、卷积、非线性激活、正则化、降维 / 升维、特征提取、池化、归一化等。

我们可以用 torch.nn 轻松创建各种神经网络层，比如：

  • nn.Linear：全连接层（常用于 MLP）
    线性层也叫全连接层，它主要把输入向量*权重矩阵+偏置【y=wx+b】，完成特征融合，多用于分类、回归的最后几层。

    fc = nn.Linear(128, 64)

  • nn.Conv2d：二维卷积层（常用于 CNN）
    它主要负责提取局部特征，主要用于图像分类（CNN）、声音识别等，能够共享权重，参数了比全连接小。

  • nn.RNN / LSTM / GRU：循环结构（用于 NLP、时序）
    主要用于处理序列、记忆、上下文。
    RNN：只能记少量上下文，容易梯度消失。
    LSTM：包含：遗忘门、输入门、输出门，可有效记住长序列，但结构复杂。
    GRU：结构更简单，效果类似 LSTM。

  • nn.ReLU、nn.Sigmoid、nn.Tanh：激活函数
    主要负责加入非线性，使得神经网络能够你和任意复杂函数来学习复杂关系

  • nn.BatchNorm1d：批归一化
    让每批数据做归一化处理，使得训练更快、收敛更稳定，降低梯度消失的风险

例如，一个两层神经网络：

import torch.nn as nn

class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(100, 64)  # 输入 100 维，输出 64 维
        self.fc2 = nn.Linear(64, 10)   # 分类到 10 类

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        return self.fc2(x)

2.损失函数（Loss Functions）：

损失函数（Loss Function）是衡量模型预测结果与真实标签之间差异的函数，它告诉模型：“你现在做得有多差？”。

我们在训练模型的目标就是不断让 Loss 变小，Loss 越小，模型越准确。

损失函数决定模型怎么学，要靠什么指标进行优化以及怎样衡量预测与真实的差异，没有损失函数，模型就不知道往哪个方向改进。

因为机器学习是一个最优化问题（optimization）：

我们不是直接告诉模型怎么做，而是通过损失函数让它“自己调整”参数。

损失函数提供方向：

  • 它的 大小 告诉模型表现好不好

  • 它的 梯度 告诉模型如何调整参数才能更好

没有损失函数，模型无法学习。

PyTorch 提供很多常用损失函数，例如：

  • nn.CrossEntropyLoss ：交叉熵损失，多分类任务最常用
    对于二分类：L = - [y \ln(\hat{y}) + (1 - y)\ln(1 - \hat{y})]
    而对于多分类（Softmax）：L = -\sum_{i=1}^{C} y_i \ln(\hat{p}_i)

  • nn.MSELoss ：回归任务
    L = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2惩罚“偏差大”的预测（平方使偏差大更痛），平滑、可微，对梯度下降极友好。

  • nn.BCELoss ：二分类
    L = -[y \cdot \log(\sigma(z)) + (1 - y)\cdot \log(1 - \sigma(z))]
    其中 σ 为 sigmoid。

示例：

criterion = nn.CrossEntropyLoss()

3.优化器（Optimizers）：

优化器的核心任务是：根据损失函数关于模型参数的导数（梯度），决定并执行参数更新的规则，让模型参数逐步朝“使损失最小化”的方向移动。

我们在训练模型的流程：

  1. 前向传播计算损失 L(θ)\mathcal{L}(\theta)L(θ)

  2. 反向传播得到梯度 ∇θL\nabla_{\theta}\mathcal{L}∇θ​L

  3. 优化器根据梯度和内部状态（如动量、二阶统计量等）计算参数更新量并应用

目标：θ←θ+Δθ，其中 Δθ 由优化器决定（通常为负方向的某个缩放）。

PyTorch 的优化器在 torch.optim 中：

import torch.optim as optim

常见的有：（ lr 代表学习率）

  • SGD：在小批次 B 上估计梯度
    \theta \leftarrow \theta - \eta \frac{1}{|B|}\sum_{i\in B}\nabla_{\theta} \ell(x_i, y_i; \theta)

    optimizer = optim.SGD(model.parameters(), lr=0.01)

  • Adam（最常用）
    m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t

    optimizer = optim.Adam(model.parameters(), lr=0.001)

  • RMSprop：对平方梯度使用指数滑动平均，解决 AdaGrad 学习率衰减过快问题
    s_t = \beta s_{t-1} + (1-\beta) g_t \odot g_t

4.训练过程：

在每个 batch 的训练中，主要流程如下：

（1）数据处理与加载：

在 PyTorch 中，处理和加载数据是深度学习训练过程中的关键步骤。为了高效地处理数据，PyTorch 提供了强大的工具，包括 torch.utils.data.Dataset 和 torch.utils.data.DataLoader，帮助我们管理数据集、批量加载和数据增强等任务。

dataset = TensorDataset(X, y)
dataloader = DataLoader(dataset, batch_size=64, shuffle=True, num_workers=2)

torch.utils.data.Dataset 是一个抽象类，允许你从自己的数据源中创建数据集。

from torch.utils.data import Dataset

class MyDataset(Dataset):
    def __init__(self, data, labels):
        self.data = data
        self.labels = labels
    # 返回数据总数量
    def __len__(self):
        return len(self.data)
    # 根据 index 返回一个样本（x, y）
    def __getitem__(self, index):
        x = self.data[index]
        y = self.labels[index]
        return x, y

我们通过 __len__ 与 __getitem__ 方法，Pytorch就能够随便访问数据。

Dataset 负责告诉 PyTorch：“你的数据在哪？怎么取？一共有多少？”

而什么是DataLoader呢？

Dataset 通过 __getitem__ 方法只返回单条数据【每次给一个index，就只返回一条样本】，但训练神经网络需要 batch 数据，假设 batch_size= 32 条，那么可能会这么分割：

第 0–31 条 → 第一批（batch 0）
第 32–63 条 → 第二批（batch 1）
第 64–95 条 → 第三批（batch 2）
...

Dataset 不会自动帮你把 32 条数据组合在一起。所以我们要一个一个去取：

for i in range(32):
    x, y = dataset[i]

但是如果这么写，需要我们自己去手动循环处理，非常麻烦。

另外，对于数据可能还要进行多种操作例如：

  • shuffle 打乱

  • batch 自动打包成 tensor

  • 多线程读取

  • 自动迭代

这就是可以用到 Pytorch 的 DataLoader 了，DataLoader 负责把 Dataset 读取成 “按批次、可迭代” 的数据流。

下面是DataLoader的参数：

DataLoader(
    dataset,            # 你写的 Dataset
    batch_size=32,      # 一个 batch 的大小
    shuffle=True,       # 每轮是否打乱
    num_workers=4,      # 多少线程加载数据（加速）
    drop_last=False     # 最后不足一批是否丢弃
)

假设我们自定义一个 dataset：

class MyDataset(Dataset):
    def __init__(self):
        self.x = torch.randn(1000, 10)   # 1000 条数据，每条维度 10
        self.y = torch.randint(0, 2, (1000,))  # 1000 个标签，每个是 0/1（分类任务）

    def __len__(self):
        return len(self.x)

    def __getitem__(self, index):
        return self.x[index], self.y[index]

我们使用 DataLoader，它会自动把 Dataset 中的单条数据打包成 batch：

dataloader = DataLoader(dataset, batch_size=32)  # 每次从 Dataset 取 32 条数据并打包成一个 batch
for x_batch, y_batch in dataloader:
    # 循环遍历
    print(x.shape)   # [32,10]
    print(y.shape)   # [32]

所以最后的处理结构大致如下：

Dataset（数据来源）
        ↓ 单条样本
DataLoader（批次加载器）
        ↓ 批次样本
训练循环 for batch in dataloader

一般在训练过程会在 DataLoader 外扩上 enumerate，它是 Python 内置函数，主要在迭代可迭代对象（如 DataLoader、list、tuple、字符串）时，自动给你加上一个“计数器”（索引编号）。

import torch
from torch.utils.data import Dataset, DataLoader

class MyDataset(Dataset):
    def __init__(self):
        self.x = torch.randn(1000, 10)
        self.y = torch.randint(0, 2, (1000,))

    def __len__(self):
        return len(self.x)

    def __getitem__(self, index):
        return self.x[index], self.y[index]

dataset = MyDataset()

dataloader = DataLoader(
    dataset,
    batch_size=32,
    shuffle=True,
    num_workers=0
)

# 使用 enumerate 迭代
# 打印加载的数据
for epoch in range(1):
    for batch_idx, (inputs, labels) in enumerate(dataloader):
        print(f'Batch {batch_idx + 1}:')
        print(f'Inputs: {inputs}')
        print(f'Labels: {labels}')

结果如下：

Batch 1:
Inputs: tensor([[ 0.4212, -1.0034,  0.9921, -0.5512, ... 共 10 列 ... ],
                [-0.3311,  0.2217,  0.7731, -0.9092, ...],
                ...
                [ 1.1029, -0.5621,  0.1183,  0.2041, ...]])   # shape = [32, 10]

Labels: tensor([1, 0, 1, 1, 0, 1, 0, 1,  ..., 0])                # shape = [32]

-----------------------------------------------------------

Batch 2:
Inputs: tensor([[ 0.1912, -0.8871, -0.2219,  0.6674, ...],
                [-0.4567,  0.1012, -1.0043,  0.3311, ...],
                ...
                [ 0.5521,  0.3098, -0.1122, -0.8874, ...]])   # shape = [32, 10]

Labels: tensor([0, 1, 1, 0, 0, 1, 0, 1, ..., 1])                  # shape = [32]

为什么 Inputs 永远是形状 [32,10]，这是因为我们的 dataset 里 x 的 shape = [1000, 10] ，batch_size = 32，所以每次 DataLoader 会自动堆叠成：

32 条数据 × 每条 10 维 → [32, 10]

而 Labels 永远是 [32]，因为每个 label 是一个标量（0 或 1），堆叠后就是：  

32 个数字 → [32]

（2）线性回归：

线性回归是最基本的机器学习算法之一，用于预测一个连续值。它是一种简单且常见的回归分析方法，目的是通过拟合一个线性函数来预测输出。

对于一个简单的线性回归问题，模型可以表示为：

y = \sum_{t=1}^T w_t x_t + b

其中 y 是预测值，xt 是输入特征，wt 是待学习的权重，b 是偏置项。

在 PyTorch 中，我们可以通过继承 nn.Module 来定义一个简单的线性回归模型：

import torch.nn as nn

# 定义线性回归模型
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        # 定义一个线性层，输入为2个特征，输出为1个预测值
        self.linear = nn.Linear(2, 1)  # 输入维度2，输出维度1
   
    def forward(self, x):
        return self.linear(x)  # 前向传播，返回预测结果

# 创建模型实例
model = LinearRegressionModel()

这里的 nn.Linear(2, 1) 表示一个线性层，它有 2 个输入特征和 1 个输出。另外 forward 方法定义了如何通过这个层进行前向传播。

（3）定义损失函数与优化器：

线性回归的常见损失函数是 均方误差损失（MSELoss），用于衡量预测值与真实值之间的差异。

PyTorch 中提供了现成的 MSELoss 函数，我们将使用 SGD（随机梯度下降） 或 Adam 优化器来最小化损失函数。

# 损失函数（均方误差）
criterion = nn.MSELoss()

# 优化器（使用 SGD 或 Adam）
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 学习率设置为0.01

（4）训练模型：

在训练过程中，我们将执行以下步骤：

  1. 使用输入数据 X 进行前向传播，得到预测值。
  2. 使用损失函数计算损失（预测值与实际值之间的差异）。
  3. 使用反向传播计算模型梯度。
  4. 根据梯度更新模型参数（权重和偏置）。

下面代码将训练模型 1000 轮，并在每 100 轮打印一次损失：

# 训练模型
num_epochs = 1000  # 训练 1000 轮
for epoch in range(num_epochs):
    model.train()  # 设置模型为训练模式

    # 前向传播
    predictions = model(X)  # 模型输出预测值
    loss = criterion(predictions.squeeze(), Y)  # 计算损失（注意预测值需要压缩为1D）

    # 反向传播
    optimizer.zero_grad()  # 清空之前的梯度
    loss.backward()  # 计算梯度
    optimizer.step()  # 更新模型参数

    # 打印损失
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/1000], Loss: {loss.item():.4f}')

我们来分析一下下面代码，num_epochs 表示整个训练集被完整训练的轮数，for epoch in range(num_epochs) 会从 0 到 999 循环，而每一次循环称为 一个 epoch，每个 epoch 模型都会对训练数据做一次完整的 前向 + 反向传播。

Pytorch 模型有两种模式：train() ，eval()

  • train() 会开启 dropout、batch normalization 等训练行为。

  • eval() 会关闭上述训练特性，用于验证或测试。

  • 即使你没有 dropout 或 batch norm，调用 train() 是一种好习惯。

  1. 前向传播：predictions = model(X)  ，model(X) 输入 X 喂进模型得到预测值。而在回归任务中，predictions 通常是 [batch_size,1] 或 [batch_size]，这个操作会记录计算图，用于后续自动求梯度。
  2. 计算损失：loss = criterion(predictions.squeeze(), Y)  ，这里的 criterion 是损失函数（例如torch.nn.MSELoss()），predictions.squeeze() 用来去掉多余维度【如果 predictions shape 是 [batch_size,1]，squeeze() 变成 [batch_size]，与 Y 维度匹配】。损失函数会计算模型预测值与真实标签的误差。注意！！！维度不匹配会报错（常见坑）。
    以均方误差（MSE）为例：\mathcal{L} = \frac{1}{B} \sum_{i=1}^{B} (\hat{y}_i - y_i)^2（B = batch size，yi = 真实值，y^i = 预测值）
  3. 清空梯度：optimizer.zero_grad()，由于 PyTorch 的梯度 会累加，默认每次 backward() 【计算梯度】都累加到已有梯度，所以每次参数更新前必须先清空梯度，否则梯度会叠加，训练异常。
  4. 反向传播：loss.backward()，PyTorch 会自动沿计算图计算每个参数的梯度，计算得到的梯度存储在每个参数的 .grad 属性中，而对 RNN 或深度网络，梯度会从输出反向传播到输入（BPTT）。
    梯度通过链式法则回到 RNN 权重：\frac{\partial \mathcal{L}}{\partial \mathbf{W}_{out}}, \quad \frac{\partial \mathcal{L}}{\partial \mathbf{W}_{ih}}, \quad \frac{\partial \mathcal{L}}{\partial \mathbf{W}_{hh}}, \quad \frac{\partial \mathcal{L}}{\partial \mathbf{b}_h}, \dots
    然后 optimizer 更新权重：\mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial \mathcal{L}}{\partial \mathbf{W}}（η = 学习率）
  5. 更新参数：optimizer.step()，根据计算得到的梯度，优化器（如 Adam 或 SGD）会更新模型权重。这一步完成一次梯度下降。

完整过程：

          +----------------------+
          |  输入 X, 标签 Y      |
          +----------------------+
                     |
                     v
          +----------------------+
          |  model.train()       |
          |  设置训练模式        |
          +----------------------+
                     |
                     v
          +----------------------+
          |  前向传播 (Forward)  |
          |  predictions = model(X) |
          +----------------------+
                     |
                     v
          +----------------------+
          |  计算损失 (Loss)      |
          |  loss = criterion(predictions, Y) |
          +----------------------+
                     |
                     v
          +----------------------+
          |  清空梯度            |
          |  optimizer.zero_grad() |
          +----------------------+
                     |
                     v
          +----------------------+
          |  反向传播 (Backward) |
          |  loss.backward()     |
          +----------------------+
                     |
                     v
          +----------------------+
          |  更新参数 (Step)      |
          |  optimizer.step()    |
          +----------------------+
                     |
                     v
          +----------------------+
          |  打印信息 / 保存模型  |
          +----------------------+
                     |
                     v
         (进入下一轮 Epoch / 结束训练)

使用RNN构建人名国家预测器

案例介绍：

我们要训练一个模型：
输入：一个人名（例如：Michael）
输出：这个人名最可能属于哪个国家（例如：USA、UK、Ireland、Chinese 等）

我们的训练集格式如下：（将其放在当前目录下的name_classfication.txt）

Ying	Chinese
Yuan	Chinese
Yue	Chinese
Yun	Chinese
Zha	Chinese
Zhai	Chinese
Zhang	Chinese
Zhi	Chinese
Zhuan	Chinese
Zhui	Chinese
Nguyen	Vietnamese
Tron	Vietnamese
Le	Vietnamese
Pham	Vietnamese
Huynh	Vietnamese

...

导包准备：

# 导入torch工具
import torch
# 导入nn准备构建模型
import torch.nn as nn
import torch.optim as optim
# 导入torch的数据源与数据迭代器工具包
from torch.utils.data import Dataset, DataLoader
# 用于获得常见字母及字符规范化
import string
# 导入时间工具包
import time
# 引入制图工具包
import matplotlib.pyplot as plt
# 进度条
from tqdm import tqdm
# 保存成json数据工具
import json

1.数据处理与加载：

我们首先需要定义字符表以及国家类别列表用于one-hot编码：

# 获取常用的字符数量
all_letters = string.ascii_letters + " ,;.'"
n_letters = len(all_letters)
# 获取国家名种类数

categories = ['Czech', 'English', 'French', 'German', 'Irish', 'Italian', 'Arabic', 'Chinese', 'Greek', 'Dutch', 'Vietnamese',
             'Japanese', 'Polish', 'Portuguese', 'Korean', 'Russian', 'Scottish', 'Spanish', 'Dutch']

print(f'常用字符数量：{n_letters}')
print(f'国家名种类数：{len(categories)}')

接下来，我们需要根据数据文件地址读取数据集返回样本x与样本y：

# 读取数据到内存
def read_data(file_path):
    # 定义两个空列表，用于存储国家名和对应的标签
    my_list_x, my_list_y = [], []
    # 读取文件内容
    with open(file_path, 'r', encoding='utf-8') as f:
        for line in f.readlines():
            # 数据清洗
            if len(line) <= 5:
                continue
            # 按照行提取样本x与样本y
            (x,y) = line.strip().split('\t')  # 去除两边空白并按tab键分隔
            my_list_x.append(x)
            my_list_y.append(y)
    # 返回样本x与样本y
    return my_list_x, my_list_y

接下来就需要自定义Dataset：

# 构建数据源
class NameClassDataset(Dataset):
    def __init__(self, my_list_x, my_list_y):
        super().__init__()
        self.my_list_x = my_list_x
        self.my_list_y = my_list_y
        # 样本数量
        self.samples_len = len(my_list_x)

    # 获取样本数量
    def __len__(self):
        return self.samples_len

    # 获取第几条样本数据
    # 到时候可以直接通过tensor_x, tensor_y = nameClassDataset[item]获取第item条样本数据
    def __getitem__(self, item):
        item = min(max(item, 0), self.samples_len - 1)
        # 获取第item条样本数据
        x = self.my_list_x[item]
        y = self.my_list_y[item]
        # 样本x one-hot编码（例如abl名字对应（3,57）的矩阵）
        x0 = torch.zeros(len(x), n_letters)
        # 遍历人名的每一个字母进行one-hot编码的赋值
        for i, letter in enumerate(x):
            x0[i][all_letters.find(letter)] = 1
        # 样本y转换为张量
        y0 = torch.tensor(categories.index(y), dtype=torch.long)
        # 返回样本x与样本y的张量
        return x0, y0

随后创建实例化dataloader对象方法：

# 实例化dataloader对象
def get_dataloader():
    my_list_x, my_list_y = read_data(file_path='name_classfication.txt')
    # 构建数据源
    dataset = NameClassDataset(my_list_x, my_list_y)
    # 封装dataset得到dataloader对象：会对数据进行增加维度
    # 参数：
    # batch_size：每个批次样本数量
    # shuffle：是否随机打乱样本顺序
    dataloader = DataLoader(dataset, batch_size=1, shuffle=True)
    return dataloader

2.构建RNN模型：

我们选择简单的RNN做序列建模，最后用一个全连结层把隐藏态映射为分类 logits，再做归一化（log-softmax）。

首先构造初始化方法__init__：

构造类参数：

  1. input_size：每个时间步输入向量维度（这里是字符 one-hot 的长度）
  2. hidden_size：RNN 隐藏层维度（隐藏向量长度）
  3. output_size：分类数（国家个数）
  4. num_layers：RNN 堆叠层数
class MyRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_layers=1):
        super().__init__()
        # input_size 代表词嵌入维度；
        self.input_size = input_size
        # hidden_size代表RNN隐藏层维度
        self.hidden_size = hidden_size
        # output_size代表：国家种类个数
        self.ouput_size = output_size
        self.num_layers = num_layers
        # 定义RNN网络层
        # 设定了batch_first=True,意味着rnn接受的input第一个参数是batch_size
        self.rnn = nn.RNN(self.input_size, self.hidden_size,
                          num_layers=self.num_layers, batch_first=True)
        # 定义输出网络层
        self.linear = nn.Linear(self.hidden_size, self.ouput_size)
        # 定义softmax层（归一化）
        # 设定dim=-1,代表对最后一个维度进行softmax
        self.softmax = nn.LogSoftmax(dim=-1)

为什么要定义线性层linear？

RNN 在处理序列时：

  • 每个时间步 t 的隐藏状态 ht 都是对输入序列前 t 个字符的 抽象表示

  • 隐藏向量 ht​ 维度是 hidden_size（比如 128），它本身没有类别的语义

  • 它是“特征向量”，类似于深度学习里卷积层输出的 feature map

换句话说：

  • h_T = 对整个人名的特征总结

  • 这些特征能帮助区分不同类别，但 不能直接告诉你哪个类别

  • 还需要一层映射，把隐藏特征空间映射到类别空间（18 个国家）

假设我们的h_T是128维的：

h_T = [0.12, -0.5, 0.8, ... 128个数字]

  • 这些数字是序列模式的表示（特征）

  • 不可能直接说“这是 English 或 French”，因为它不是类别空间

  • 全连接层（Linear）就是把这个 128 维特征向量 投影到 18 维类别向量：

    Linear(h_T) -> logits = [2.3, -1.5, 0.8, ...]  # 18维
logit是什么？

logit 不是概率，它是“分类分数”或“未经归一化的预测值”。在数学上，logit 就是神经网络最后一层线性输出：logits=W⋅h+b

对应每个类别一个实数，例如有 18 个国家：

logits = [2.3, -1.5, 0.8, 0.0, ...]  # 18 个数

它们可以是正数，也可以是负数，没有限制，总和也不一定等于 1。只是“模型对每个类别的倾向分数”，数值越大表示模型越倾向这个类别。

可以理解为：logit 是“原始的评分”，还没有转换成真正的概率。

PyTorch 的 nn.Linear(in_features, out_features) 做的就是 线性变换（仿射变换）：

\text{logits} = W \cdot h_T + b

\begin{bmatrix} \text{logit}_1 \\ \text{logit}_2 \\ \vdots \\ \text{logit}_{18} \end{bmatrix} = \begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1,128} \\ w_{21} & w_{22} & \cdots & w_{2,128} \\ \vdots & \vdots & \ddots & \vdots \\ w_{18,1} & w_{18,2} & \cdots & w_{18,128} \end{bmatrix} \begin{bmatrix} h_1 \\ h_2 \\ \vdots \\ h_{128} \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{18} \end{bmatrix}

我们可以想象成隐藏向量 h_T 是一个 128 个特征的特征图，而 Linear 就像一个 “评分模板集合”，有 18 个模板，每个模板对应一个类别，点乘特征向量 → 得到每个类别的总分（logit），这 18 个分数就是模型对每个类别的倾向。

为什么要在加一个softmax呢？

归一化（Normalization），在机器学习和神经网络中，指的是把一组数值转换到一个统一的标准范围或概率分布。

因为 linear 输出的是：\text{logits} = W \cdot h_T + b

维度 [output_size]，每个元素是一个实数（可以为正、负、大、或小），比如 [2.3, -1.5, 0.8, ...]，这些只是分数（logit），不能直接作为概率，也不能解释为“属于某个类别的可能性”。

而 Softmax 的作用：把 logit 转成概率分布

P(y=i \mid x) = \frac{e^{\text{logit}_i}}{\sum_{j=1}^{18} e^{\text{logit}_j}}

  • 每个类别对应的值 ∈ [0, 1]

  • 所有类别概率和 = 1

  • 可以直观解释为“模型认为输入属于该类别的概率”

假设我们的模型预测输出 logits 为：

logits=[2.0,1.0,0.1,−0.5,0.3,...,0.0](18维)

  • 这是模型给每个国家打的分数，越大表示模型越倾向该类别。

  • 还不是概率，不能直接说“这是 Czech 的概率”。

用 Softmax 归一化后：

P(y=i∣name)=Softmax(logits)≈[0.61,0.23,0.04,0.02,0.03,...,0.01]

  • 模型认为输入名字属于 第一个国家（例如 English）的概率 0.61，属于第二个国家概率 0.23，其他国家概率很小。

  • 归一化的意义：把任意实数 logits 转成可解释的概率，方便做预测和训练。

大部分分类任务使用 交叉熵损失（CrossEntropyLoss），交叉熵需要输入概率分布或 log 概率，如果不归一化，loss 就无法正确计算。

注：PyTorch 的 nn.CrossEntropyLoss 内部已经帮我们做了 LogSoftmax，所以你在模型里其实可以直接输出 logits，不显式加 Softmax 也行。

然后接下来继续完善构建RNN：

构建他的前向传播以及对于隐藏层h0的初始化：

class MyRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_layers=1):
        super().__init__()
        # ...

    def forward(self, x, h0):
        # x代表输入的样本数据[seq_len, input_size]
        # hidden代表隐藏层状态[num_layers, batch_size, hidden_size]
        # x是二维的，需要增加一个维度，变成[batch_size, seq_len, input_size]
        x0 = x.unsqueeze(0)
        # 输入RNN层
        out, h1 = self.rnn(x0, h0)
        # 获取最后一个单词的隐藏层张量代表整个人名
        tmpout = out[:, -1, :]   # [batch, hidden_size]
        # result --> [1, 18]
        tmpout = self.linear(tmpout)
        return self.softmax(tmpout), h1

    def init_hidden(self):
        # 初始化隐藏层状态为0
        return torch.zeros(self.num_layers, 1, self.hidden_size)

为什么要加入x.unsqueeze(0)？

在初始化 RNN 时写了：

self.rnn = nn.RNN(self.input_size, self.hidden_size, num_layers=self.num_layers, batch_first=True)

batch_first=True 表示 RNN 期望输入 input 的形状为：[batch_size,seq_len,input_size]

而在 forward 函数中：

x.shape  # [seq_len, input_size] = [3, 57]

  • 只有两个维度：时间步 + 特征

  • 没有 batch 维度，而 RNN 要求输入必须有 batch 维度

unsqueeze(0) 的作用是会在指定维度插入一个大小为 1 的维度，这里 dim=0，所以在最前面增加了 batch 维度：x:[seq_len,input_size]→x0:[1,seq_len,input_size]

3.使用RNN训练模型：

首先读取文档并构建数据源：（读取名字和国家标签，构建 PyTorch Dataset）

my_list_x, my_list_y = read_data(file_path='name_classfication.txt')
dataset = NameClassDataset(my_list_x, my_list_y)

这里的维度表示：

  • x：名字 → [seq_len, input_size]，比如 seq_len=3，input_size=57

  • y：国家标签 → [1]（整数索引）

之后初始化数据：

input_size = 57
hidden_size = 128
ouput_size = 18
rnn_model = MyRNN(input_size, hidden_size, ouput_size)
cross_entropy = nn.NLLLoss()
adam = optim.Adam(rnn_model.parameters(), lr=mylr)

  • 定义模型、损失函数、优化器

  • NLLLoss 对应模型输出 LogSoftmax 后的概率 log

这里的 RNN 隐藏状态 h0： [num_layers, batch_size, hidden_size] → [1, 1, 128]

接下来训练循环（epoch → batch）：

for epoch_idx in range(epochs):
    my_dataloader = DataLoader(dataset, batch_size=1, shuffle=True)
    for idx, (x, y) in enumerate(tqdm(my_dataloader)):
        h0 = rnn_model.inithidden()
        output, hn = rnn_model(x[0], h0)

对每条数据进行训练，初始化隐藏状态 h0 为 0，通过 RNN 前向传播得到 output（预测 log-prob）和 hn（最后隐藏状态）。

维度：

  1. x[0]： [seq_len, 57]

  2. h0： [1, 1, 128]

  3. out（RNN 输出）: [1, seq_len, 128]

  4. tmpout = out[:, -1, :] → [1, 128]

  5. linear(tmpout) → [1, 18]

  6. softmax(tmpout) → [1, 18]

随后进行损失计算->反向传播+参数更新：

my_loss = cross_entropy(output, y)  # 计算预测值和真实标签的负对数似然损失
adam.zero_grad()   # 清空梯度
my_loss.backward()  # 计算梯度
adam.step()        # 用 Adam 优化器更新参数

之后打印日志不过多叙述，然后保存训练结果：

dict1 = {"avg_loss": total_loss_list,
         "all_time": total_time,
         "avg_acc": total_acc_list}
with open('./save_results/ai_rnn.json', 'w') as fw:
    fw.write(json.dumps(dict1))

完整训练代码：

mylr = 1e-3  # 学习率
epochs = 1   # 训练轮次
def train_rnn():
    # 读取文档数据
    my_list_x, my_list_y = read_data(file_path='name_classfication.txt')
    # 构建数据源
    dataset = NameClassDataset(my_list_x, my_list_y)
    # 实例化模型
    input_size = 57
    hidden_size = 128
    ouput_size = 18
    # 实例化RNN模型
    rnn_model = MyRNN(input_size, hidden_size, ouput_size)
    # 实例化损失函数对象
    cross_entropy = nn.NLLLoss()
    # 实例化优化器对象
    adam = optim.Adam(rnn_model.parameters(), lr=mylr)
    # 定义训练模型的打印日志的参数
    start_time = time.time()
    total_iter_num = 0  # 当前已经训练的样本总数
    total_loss = 0  # 已经训练的损失值和 
    total_loss_list = []  # 每隔n个样本，保存平均损失值
    total_acc_num = 0  # 预测正确的样本个数
    total_acc_list = []  # 每隔n个样本，保存平均准确率
    # 开始训练
    for epoch_idx in range(epochs):
        # 实例化dataloader对象
        my_dataloader = DataLoader(dataset, batch_size=1, shuffle=True)
        # 开始内部数据的迭代
        for idx, (x, y) in enumerate(tqdm(my_dataloader)):
            h0 = rnn_model.inithidden()
            # 将数据注入模型
            output, hn = rnn_model(x[0], h0)
            # 计算损失
            my_loss = cross_entropy(output, y)
            # print(f'my_loss--》{my_loss}')
            # print(f'my_loss--》{type(my_loss)}')
            # 梯度清零
            adam.zero_grad()
            # 反向传播: 计算梯度
            my_loss.backward()
            # 梯度更新
            adam.step()

            # 记录日志
            # 统计一下已经训练样本的总个数
            total_iter_num = total_iter_num + 1
            # 统计一下已经训练样本的总损失
            total_loss = total_loss + my_loss.item()
            # 统计已经训练的样本中预测正确的个数
            i_predict_num = 1 if torch.argmax(output).item() == y.item() else 0
            total_acc_num = total_acc_num + i_predict_num
            # 每隔100次训练保存一下平均损失和准确率
            if total_iter_num % 100 == 0:
                avg_loss = total_loss / total_iter_num
                total_loss_list.append(avg_loss)
                avg_acc = total_acc_num / total_iter_num
                total_acc_list.append(avg_acc)
            # 每隔2000次训练打印一下日志
            if total_iter_num % 2000 == 0:
                temp_loss = total_loss / total_iter_num
                temp_acc = total_acc_num / total_iter_num
                temp_time = time.time() - start_time
                print('轮次:%d, 损失:%.6f, 时间:%d，准确率:%.3f' % (epoch_idx + 1, temp_loss, temp_time, temp_acc))
        # 每一轮都保存模型
        torch.save(rnn_model.state_dict(), './save_model/ai20_rnn_%d.bin' % (epoch_idx + 1))
    # 计算总时间
    total_time = int(time.time() - start_time)
    print('训练总耗时：', total_time)
    # 将结果保存到文件中
    dict1 = {"avg_loss": total_loss_list,
             "all_time": total_time,
             "avg_acc": total_acc_list}
    with open('./save_results/ai_rnn.json', 'w') as fw:
        fw.write(json.dumps(dict1))
    return total_loss_list, total_time, total_acc_list

4.基于训练好的模型构造预测函数：

# 数据预处理：将数据转化one-hot编码
def line2tensor(x):
    # x-->"bai"
    tensor_x = torch.zeros(len(x), n_letters)
    # one-hot表示
    for li, letter in enumerate(x):
        tensor_x[li][all_letters.find(letter)] = 1

    return tensor_x
"""
    1.获取数据
    2.数据预处理：将数据转化one-hot编码
    3.实例化模型
    4.加载模型训练好的参数: model.load_state_dict(torch.load("model_path"))
    5.with torch.no_grad():
    6.将数据送入模型进行预测（注意:张量的形状变换）
"""
# 构造rnn预测函数
def rnn_predict(x):
    # 将数据x进行张量的转换
    tensor_x = line2tensor(x)
    # 加载训练好的模型
    my_rnn = MyRNN(input_size=57, hidden_size=128, output_size=18)
    # 加载已经训练好的权重文件，让模型恢复到训练好的状态
    my_rnn.load_state_dict(torch.load('./save_model/ai20_rnn_3.bin'))
    # 实现模型的预测(禁用梯度计算）
    with torch.no_grad():
        # 将数据送入模型
        output, hn = my_rnn(tensor_x, my_rnn.inithidden())
        print(f'output--》{output}')
        # 获取output最大的前3个值
        # output.topk(3, 1, True)
        values, indexes = torch.topk(output, k=3, dim=-1, largest=True)
        print(f'values-->{values}')
        print(f'indexes-->{indexes}')
        for i in range(3):
            value = values[0][i]
            index = indexes[0][i]
            category = categories[index]
            print(f'当前预测的值是：{value}, 国家类别是：{category}')

5.整个训练流程维度变化分析：

最开始的数据集如下：

  1. x：名字，例如“Bai”
  2. y：国家名，例如“Chinese”

在使用one-hot编码后：

x0 = torch.zeros(len(x), n_letters)
for i, letter in enumerate(x):
    x0[i][all_letters.find(letter)] = 1

原来的名字“Bai” -> [seq_len]  =>  seq_len = 3

那么数据经过 Dataset 输出：x0的维度为 [3,57]，y0则为 [1]。

在使用 DataLoader 批次封装：

dataloader = DataLoader(dataset, batch_size=1, shuffle=True)

由于 batch_size = 1，所以x0的维度变为 [1,3,57]，y0则为 [1]。

模型的h0隐藏层是全0，其维度是 [1,1,128]。

h0 = rnn_model.init_hidden()  
# shape: [num_layers, batch_size, hidden_size] = [1, 1, 128]

接下来前向传播：

x0 = x.unsqueeze(0)  # shape: [1, seq_len, input_size] = [1, 3, 57]
out, h1 = rnn_model.rnn(x0, h0)

输入x0的维度是 [1,3,57]，而输出维度是 [1,3,128]，隐藏层维度仍是 [1,1,128]。

【out 的每个时间步都对应一个隐藏状态，包含每个字母的特征】

在提取最后时间步的隐藏状态：

tmpout = out[:, -1, :]  # 取最后时间步

[batch_size, hidden_size] = [1,128]，因为我们使用最后一个字符的隐藏状态表示整个名字特征（encoding）。

接下来全连接层（linear），输入[1,128]输出[1,18]，把隐藏状态 [128] 映射到 18 个国家类别的 logit 分数。

随后进行归一化处理维度仍然是[1,18]，这是为了将线性输出 logits 转换成类别概率（log 概率），方便与 NLLLoss 计算损失。

步骤 张量 维度 说明
原始名字 "bai" seq_len=3 字符串
One-hot 编码 tensor_x [3, 57] 每个字符 one-hot
增加 batch x0 [1, 3, 57] batch=1
初始化隐藏状态 h0 [1, 1, 128] 全零
RNN 输出 out [1, 3, 128] 每个时间步的隐藏状态
取最后时间步 tmpout [1, 128] 表示整个人名特征
Linear 映射 [1, 18] logits
LogSoftmax [1, 18] 类别 log 概率
Top-3 预测 values, indexes [1, 3] 最大 3 类别及其概率
# pytorch # rnn # 深度学习
Logo
火山引擎 ADG 社区

火山引擎开发者社区是火山引擎打造的AI技术生态平台，聚焦Agent与大模型开发，提供豆包系列模型（图像/视频/视觉）、智能分析与会话工具，并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长，新用户可领50万Tokens权益，助力构建智能应用。

更多推荐

Chess用户界面设计：Tailwind CSS样式系统和组件库

GitHub推荐项目精选中的ch/chess是一个类似chess.com的多人在线象棋平台，它采用现代化的前端技术栈构建，尤其在用户界面设计上通过Tailwind CSS样式系统和组件库实现了优雅且功能丰富的交互体验。本文将深入探讨该项目如何利用Tailwind CSS打造一致的设计语言和高效的组件系统，为象棋爱好者提供沉浸式的游戏界面。## 🎨 Tailwind CSS样式系统：构建统一视

avatar 火山引擎 ADG 社区

终极指南：GPT-Engineer如何通过AI自动发现代码问题并提升质量

GPT-Engineer是一款强大的AI驱动代码工具，它能帮助开发者自动检测潜在代码问题、优化代码质量，让编程效率提升3倍以上。无论是新手还是资深开发者，都能通过这款工具轻松发现代码中的隐藏缺陷，减少调试时间，释放更多精力在创造性工作上。## 一键发现代码问题：GPT-Engineer的AI审查魔力GPT-Engineer的核心能力在于其内置的智能代码分析系统。通过集成Python代码格式

avatar 火山引擎 ADG 社区

SatDump中的纠错编码技术：从RS码到Turbo码的完整实现指南

在卫星数据传输过程中，信号往往会受到各种干扰，导致数据错误。SatDump作为一款通用卫星数据处理软件，集成了多种先进的纠错编码技术，确保从卫星接收到的数据能够准确解码。本文将深入解析SatDump中从Reed-Solomon（RS）码到Turbo码的实现细节，帮助读者理解这些技术如何保障卫星通信的可靠性。## 为什么纠错编码对卫星数据至关重要？卫星与地面站之间的通信链路面临着空间辐射、大

avatar 火山引擎 ADG 社区