来源：
*《第五章 深度强化学习 Q网络》.ppt --周炜星、谢文杰

文章目录

一、前言

Q表格、Q网络与策略函数
在这里插入图片描述
在这里插入图片描述

Q表格是有限的离散的，而神经网络可以是无限的。

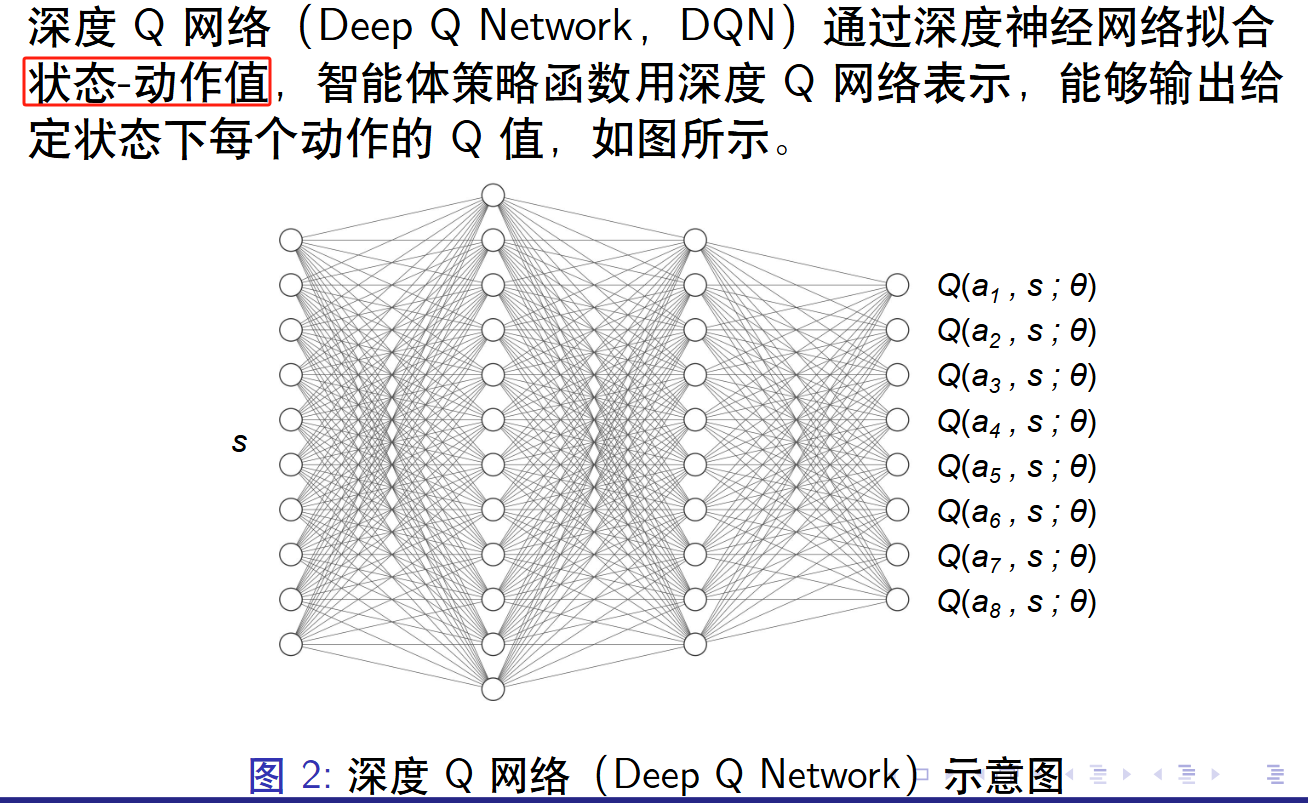
在这里插入图片描述

对于动作有限的智能体来说，使用Q网络获得当下状态的对于每个动作的 状态-动作值 。那么 arg max ⁡ Q ( a , s ; θ ) = a b e s t \argmax Q(a,s; \theta) =a_{best} argmaxQ(a,s;θ)=abest​ ,那么我们对当前的状态s,会有一个最佳的选择 a b e s t a_{best} abest​ ,选择的依据是策略 θ \theta θ. 我们的目标是获得最优的策略 θ ∗ \theta^* θ∗.即优化 θ \theta θ,显然神经网络可以通过梯度下降的方法获得最优的策略 θ ∗ \theta^* θ∗.

二、Q-learning

DQN 算法全称是 Deep Q Network，基于经典强化学习算法 Q-learning 演化而来，Q-learning 作为强化学习的重要算法，有
着悠久的历史，在强化学习发展和应用过程中发挥了重要作用.在 Q-learning 算法中，状态-动作值函数 Q(s, a) 的更新公式为:
在这里插入图片描述

  1. Q-learning是借助于 Q-Table 的， 不存在 策略隐形表达(即关于 θ \theta θ的参数)
  2. 其MDP chain为： S → a / r S ′ → a ′ / r ′ S ′ ′ → ⋯ S \stackrel{a/r}→S'\stackrel{a'/r'}→S'' \to \cdots S→a/rS′→a′/r′S′′→⋯ 状态S在动作a下变为状态S’,并获得及时奖励r;……

2.1 代码示例

import numpy as np
import random

# 定义网格世界环境
class GridWorld:
    def __init__(self, rows, cols, start, goal):
        self.rows = rows
        self.cols = cols
        self.start = start
        self.goal = goal
        self.state = start

    def reset(self):
        self.state = self.start
        return self.state

    def step(self, action):
        x, y = self.state
        if action == 0:  # 上
            x = max(x - 1, 0)
        elif action == 1:  # 下
            x = min(x + 1, self.rows - 1)
        elif action == 2:  # 左
            y = max(y - 1, 0)
        elif action == 3:  # 右
            y = min(y + 1, self.cols - 1)
        
        self.state = (x, y)
        reward = -1  # 每一步的惩罚
        done = self.state == self.goal
        if done:
            reward = 100  # 到达目标的奖励
        return self.state, reward, done

# Q-learning 算法
class QLearning:
    def __init__(self, env, alpha=0.1, gamma=0.99, epsilon=0.1, episodes=1000):
        self.env = env
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # 探索率
        self.episodes = episodes
        self.q_table = np.zeros((env.rows, env.cols, 4))  # Q 表 ，初始为全0

    def choose_action(self, state):
        if random.uniform(0, 1) < self.epsilon:
            return random.choice([0, 1, 2, 3])  # 探索
        else:
            return np.argmax(self.q_table[state])  # 利用

    def train(self):
        for episode in range(self.episodes):
            state = self.env.reset()
            done = False
            while not done:
                action = self.choose_action(state)  #根据当前的状态，按照epsion策略选择动作(可能随机，可能最佳)
                next_state, reward, done = self.env.step(action)
                best_next_action = np.argmax(self.q_table[next_state]) #获得next_state根据Q表格最好的动作
                td_target = reward + self.gamma * self.q_table[next_state][best_next_action]
                #根据 next_state 和 best_next_action 获得未来的收益，再加上即使奖励reward,即当前的状态和动作的价值
                td_error = td_target - self.q_table[state][action]
                self.q_table[state][action] += self.alpha * td_error
                state = next_state
            if (episode + 1) % 100 == 0:
                print(f"Episode {episode + 1}/{self.episodes} completed")

    def test(self):
        state = self.env.reset()
        done = False
        path = [state]
        while not done:
            action = np.argmax(self.q_table[state])
            state, _, done = self.env.step(action)
            path.append(state)
        print("Path taken:", path)

# 主程序
if __name__ == "__main__":
    # 定义网格世界
    rows, cols = 5, 5
    start = (0, 0)
    goal = (4, 4)
    env = GridWorld(rows, cols, start, goal)

    # 初始化 Q-learning
    q_learning = QLearning(env, alpha=0.1, gamma=0.99, epsilon=0.1, episodes=1000)

    # 训练
    q_learning.train()

    # 测试
    q_learning.test()

三、DQN

深度强化学习算法中值函数或策略函数一般使用深度神经网络逼近或近似，用 参数化的状态-动作值函数 Q(s, a; θ) 逼近 Q(s, a)，可如下表示
在这里插入图片描述
深度强化学习算法在更新过程中不直接对状态-动作值函数Q(s, a; θ) 的数值进行更新，而是更新近似状态-动作值函数Q(s, a; θ) 的深度神经网络模型参数 θ，可表示为
在这里插入图片描述

3.1 Experience Replay 经验回放

经典的 DQN 算法中有一个关键技术，叫经验回放。智能体在与环境交互过程中获得的经验数据会保存在 经验池（Replay Buffer）之中。经验池中的数据存放形式如下：
在这里插入图片描述
经验池存储满后，我们可以将旧的经验样本数据剔除，保存新的经验样本数据.

from collections import deque
# 创建一个最大长度为 5000 的 deque
dq = deque(maxlen=5000)
# 向 deque 中添加元素
for i in range(5005):
    dq.append([单一经验条(见Eq.5)])

经验存储

self.replay_buffer = deque(maxlen=buffer_size) ##预先定义的存储池，下为存储命令
def store_experience(self, state, action, reward, next_state, done):
      self.replay_buffer.append((state, action, reward, next_state, done))

批量采样

batch = random.sample(self.replay_buffer, self.batch_size)
###上面是抽样，下面是数据格式转化
states, actions, rewards, next_states, dones = zip(*batch)

states = torch.tensor(states, dtype=torch.float32)
actions = torch.tensor(actions, dtype=torch.int64)
rewards = torch.tensor(rewards, dtype=torch.float32)
next_states = torch.tensor(next_states, dtype=torch.float32)
dones = torch.tensor(dones, dtype=torch.float32)

3.2 目标网络

目标：我们要更新 Q ( s , a ; θ ) Q(s,a;\theta) Q(s,a;θ)中的参数 θ \theta θ,那么具体怎么更新呢？
已知：

  1. Q-learning的更新公式 (Eq.1 )，有当前的状态-动作值Q(s,a)(Q表格中的值与真正的值有误差的) 会随着 迭代关系 逐渐接近 真正的状态-动作值。
    r + γ max ⁡ a ′ Q ( s ′ , a ′ ) r +\gamma \max_{a'} Q(s',a') r+γmaxa′​Q(s′,a′) =当下奖励+未来的增益
    G a i n t = r + γ G a i n t + 1 Gain_t =r +\gamma Gain_{t+1} Gaint​=r+γGaint+1​
    在Q-learing中其实默认了一种策略，就是选择next_state中best_next_action.即选择使下一个状态收益最大的动作。
    由于Q-表格 是有限的，随着迭代次数的增加，所以状态是会大量重复出现，且(状态-动作值)会逐渐有区分，所以会有
    在这里插入图片描述
  2. DQN算法根据Q-learn改编过来的。即有目标如下：
    Q ( s , a ； θ ) → ( r + γ max ⁡ a ′ Q ( s ′ , a ′ ; θ ∗ ) ) Q(s,a；\theta) \to \quad (r+\gamma \max_{a'}Q(s',a';\theta^*)) Q(s,a；θ)→(r+γa′max​Q(s′,a′;θ∗))
    且有 θ \theta θ是当下的策略， θ ∗ \theta^* θ∗是最终的最佳策略。那么显然，当我们处于 θ \theta θ的策略的时候(起点)，我们无法直接找到 θ ∗ \theta^* θ∗(终点).为什么不能直接找到？(因为可能不收敛)

测试：
假设有一个DQN网络已经定义好了(如3.3)。那么智能体有 Q-网络(即状态-动作值函数网络), 优化器, 损失函数.如下所示：

class DQN_Agent:
    def __init__(self,)
    		###省略了很多
        self.q_network = DQN(self.state_dim, self.action_dim) #在线网络，Q网络
        self.optimizer = optim.Adam(self.q_network.parameters(), lr=self.lr)#优化器
        self.loss_fn = nn.MSELoss() #损失函数

没有目标网络直接优化：

Q t a r g e t = R t + γ ⋅ max ⁡ Q ( n e x t s t a t e , a c t i o n ) Q_{target}=R^t+ \gamma \cdot \max Q(nextstate ,action) Qtarget​=Rt+γ⋅maxQ(nextstate,action)
Q c a l c u l a t e = Q ( c u r r e n t s t a t e ) Q_{calculate} =Q(currentstate) Qcalculate​=Q(currentstate)

###没有目标网络的时候，计算Q_target是用相同的Q网络计算的
q_values = self.q_network(states) #Q(current_state)
next_q_values = self.q_network(next_states) #Q(next_curente)
q_target = q_values.clone()

for i in range(self.batch_size):
    if dones[i] == 1:
        q_target[i, actions[i]] = rewards[i]
    else:
        q_target[i, actions[i]] = rewards[i] + self.gamma * torch.max(next_q_values[i])

loss = self.loss_fn(q_values, q_target)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()

❓问题：Q 网络的更新可能会导致目标值（q_target）和预测值（q_values）之间的相关性过高。这种高相关性会导致训练过程不稳定，甚至发散。
✋解决：我们在中间增加了一个目标网络Target network作为中点(过渡点)。
目标网络的作用
目标网络是一个固定频率更新的网络，它的参数不是每次训练都更新，而是定期从主网络（也称为在线网络）复制过来。这样做的目的是为了降低目标值和预测值之间的相关性，从而提高训练的稳定性

  1. 目标网络 同原来的神经网络(被称为 行为网络behavior network) 的结构完全相同.因此，Q网络(在线网络，动作-状态值函数网络)初始化。
    初始阶段：根据设定的 结构 和随机初始化参数 θ \theta θ. 见方法一中，参数结构分为三层：输入层self.fc1(设定的是全连接网络)，隐藏层self.fc2(设定的是全连接)，输出层self.fc3(设定的是全链接网络)。而方法二中，我们增加新的结构(即卷积网络)，也固定了 θ \theta θ的参数的随机初始化(高斯分布)。
  2. 初始阶段目标网络同Q网络相同。只是更新频率和更新方式不同！！！ Q-网络是通过 优化器(根据梯度下降法)每次迭代更新一次参数，Target-网络 更新速度慢于前者，且是通过直接复制参数的方法更新！
### 目标网络 初始的复制过程
self.q_network = DQN(self.state_dim[0], self.action_dim)  # 在线网络
self.target_network = DQN(self.state_dim[0], self.action_dim)  # 目标网络，结构复制
self.target_network.load_state_dict(self.q_network.state_dict())  # 初始化目标网络，参数复制

self.target_network.eval()  # 设置为目标网络模式
self.optimizer = optim.Adam(self.q_network.parameters(), lr=self.lr)
self.loss_fn = nn.MSELoss()
self.target_update_frequency = target_update_frequency  # 目标网络更新频率
self.update_count = 0  # 更新计数器

####中间省略了
#####更新频率 ，

q_values = self.q_network(states)  # 使用在线网络计算 Q 值
next_q_values = self.target_network(next_states)  # 使用目标网络计算下一个状态的 Q 值 
####值得提醒的是，这里用的是taget_network，而不是Q_network,与上一段代码不同
q_target = q_values.clone()

for i in range(self.batch_size):
    if dones[i] == 1:
        q_target[i, actions[i]] = rewards[i]
    else:
        q_target[i, actions[i]] = rewards[i] + self.gamma * torch.max(next_q_values[i])

loss = self.loss_fn(q_values, q_target)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step() ###这一小部分是优化器对self.q_network的更新，即每轮训练就会更新一次Q-newrok

# 更新目标网络
self.update_count += 1
if self.update_count % self.target_update_frequency == 0:
    self.target_network.load_state_dict(self.q_network.state_dict())
    ##### 目标网络的更新的步幅是self.target_update_frequency ,且不是通过优化器更新的，而是直接对Q-network参数的复制

3.3 DQN的网络定义案例

## 方法一
class DQN(nn.Module):
   def __init__(self, input_dim, output_dim):
       super(DQN, self).__init__()
       self.fc1 = nn.Linear(input_dim, 128)
       self.fc2 = nn.Linear(128, 128)
       self.fc3 = nn.Linear(128, output_dim)
   def forward(self, x):
       x = torch.relu(self.fc1(x))
       x = torch.relu(self.fc2(x))
       x = self.fc3(x)
       return x
### 方法二：使用高斯分布对参数进行随机初始化
# 定义DQN网络
class DQN(nn.Module):
   def __init__(self, input_channels, output_dim):
       super(DQN, self).__init__()
       # 第一层：卷积层
       self.conv1 = nn.Conv2d(input_channels, 16, kernel_size=3, stride=1, padding=1)
       self.fc1 = nn.Linear(16 * 8 * 8, 128)  # 将卷积层的输出展平
       self.fc2 = nn.Linear(128, 128)
       self.fc3 = nn.Linear(128, output_dim)
       self.initialize_weights()

   def forward(self, x):
       x = torch.relu(self.fc1(x))
       x = torch.relu(self.fc2(x))
       x = self.fc3(x)
       return x

   def initialize_weights(self):
       # 使用高斯分布初始化权重
       for layer in self.modules():
           if isinstance(layer, nn.Linear):
               nn.init.normal_(layer.weight, mean=0.0, std=0.1)  # 高斯分布，均值为0，标准差为0.1
               if layer.bias is not None:
                   nn.init.constant_(layer.bias, 0.0)  # 偏置初始化为0

3.4 环境交互

在与环境交互过程中，智能体采用 ϵ-贪心策略生成轨迹，ϵ-贪心策略表示为
在这里插入图片描述
以代码为例

###选择动作的策略
def choose_action(self, state):
    if random.random() < self.epsilon:
        return random.randint(0, self.action_dim - 1) #随机选择
    else:
        state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)  # 添加批次维度
        q_values = self.q_network(state)
        return torch.argmax(q_values).item() ##目标网络值最大的动作

3.5 损失函数

损失函数 值得是 预测值和实际值之间的误差。
实际值(或者说 TD目标值),根据公式定义来计算。
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
其损失函数代码和网络的更新 见3.3 。

3.6 伪代码

在这里插入图片描述

四、DQN与DDQN关系

DDQN（Double Deep Q-Network）是基于DQN（Deep Q-Network）的改进版本，主要针对DQN中存在的“高估”问题进行了优化。

4.1 DQN 存在的Q值高估问题

参考链接：

过估计问题的原因有很多，主要是由值函数迭代逼近或优化过程中的最大化操作 maxa Q(s, a) 引入。经典 DQN 中的 TD 目标计算公式为：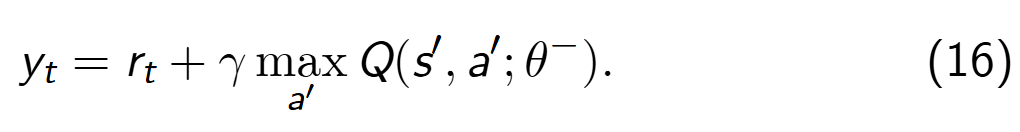
在这里插入图片描述
其中，θ是网络参数。由于同一个网络既用于选择动作（ m a x a ′ max_{a′} maxa′​​），又用于评估动作的价值（Q(s′,a′;θ)），这会导致高估Q值，尤其是当网络的估计不够准确时。

4.2 DDQN的改进思想

DDQN的核心思想是将动作选择和动作价值评估分开，使用两个网络来分别完成这两个任务，从而减少高估问题。
两个网络：

  • 在线网络（Online Network）：用于选择动作，即计算当前状态下的所有动作的Q值，并选择Q值最高的动作。
  • 目标网络（Target Network）：用于评估动作的价值，即计算目标值。

将 TD 目标计算公式(指Eq.16)等价变换后，可重写为: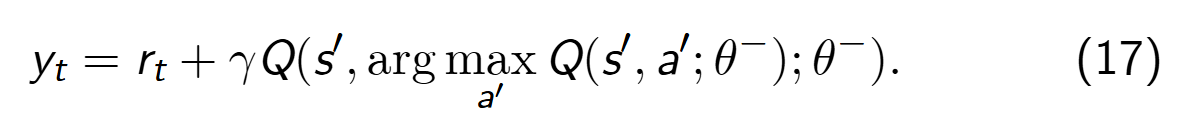
在这里插入图片描述

其中，θ是在线网络的参数，θ−是目标网络的参数。
因此，DQN 算法中的 TD 目标计算可以分解成两步来进行，第一步为选择最优动作.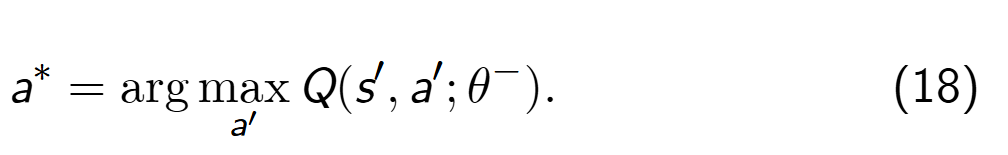
在这里插入图片描述
第二步为计算最优动作 a∗ 对应的 TD 目标值：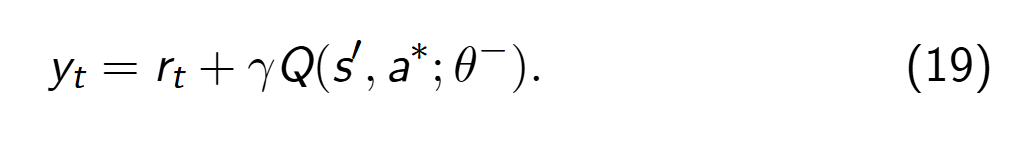
在这里插入图片描述
💡改进
在计算 DQN 算法中 TD 目标值的过程中，动作选择和动作价值评估都选择了目标网络 Q(s′, a′; θ−)。为了克服过估计问题，双Q 网络（Double DQN）算法将动作选择和动作评估做了改进。

双 Q 网络的思想简单易懂，在智能体训练中计算 TD 目标值时，分离动作选择过程和动作评估过程，使用不同网络进行函数近似。经典 DQN 算法中已经构建了两个网络，即主网络（行为网络）和目标网络。Double DQN 算法使用主网络（行为网络）选择动作

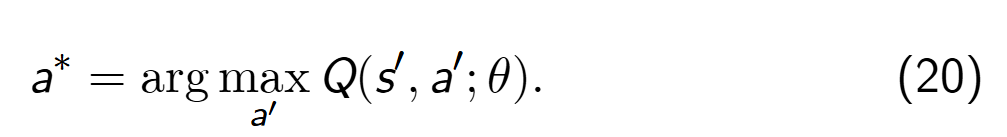
在这里插入图片描述
同时，Double DQN 算法用目标网络进行动作评估，计算最优动作对应的 TD 目标值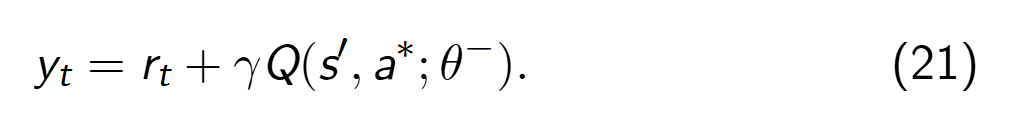
在这里插入图片描述
融合动作选择和动作评估过程，我们可以得到 TD 目标值为：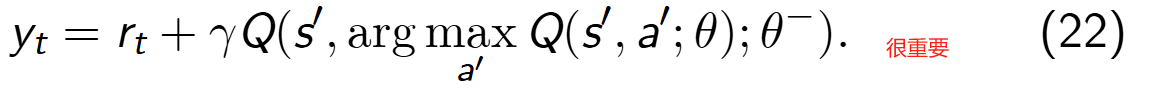
在这里插入图片描述

4.3 DDQN损失函数

DDQN与DQN不同的是在计算TD值的时候：

  • DQN使用目标网络选择动作和评估动作
  • DDQN使用在线网络选择动作，使用目标网络评估动作

在DDQN中，损失函数 L(θ) 通常定义为预测的Q值 Q(si​,ai​;θ) 与目标值 yi​ 之间的均方误差（MSE）：
L ( θ ) = E [ ( Q ( s i ​ , a i ​ ; θ ) − y i ​ ) 2 ] L(θ)=E[(Q(s_i​,a_i​;θ)−y_i​)^2] L(θ)=E[(Q(si​​,ai​​;θ)−yi​​)2]
其中，yi​ 是目标值，计算公式为(参考Eq.22)：
y i ​ = r t ​ + γ Q ( s ′ , arg max ⁡ a ′ ​ Q ( s ′ , a ′ ; θ ) ; θ − ) y_i​=r_t​+γQ(s′,\argmax_{a′}​Q(s′,a′;θ);θ−) yi​​=rt​​+γQ(s′,a′argmax​​Q(s′,a′;θ);θ−)

4.4 参数的更新方向

根据Eq.22.我们很容易得到TD误差：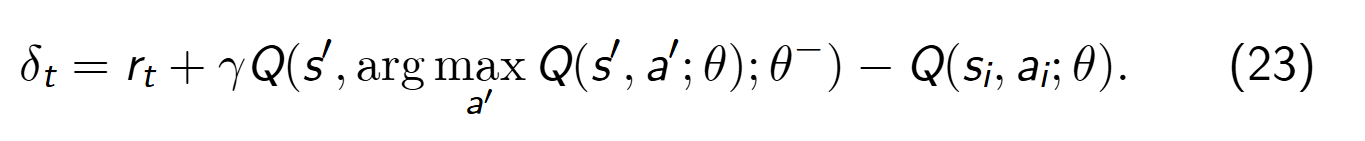
在这里插入图片描述

  • 右侧减号前为 目标值，减号后为预测值。

参数调整目标

最小化损失函数 L(θ)。这意味着我们需要调整参数 θ，使得预测的Q值 Q ( s i ​ , a i ​ ; θ ) Q(s_i​,a_i​;θ) Q(si​​,ai​​;θ) 尽可能接近目标值 y i y_i yi​​。
参数调整方向
为了最小化损失函数，我们使用梯度下降方法。具体来说，我们计算损失函数 L(θ) 关于参数 θ 的梯度，并沿着梯度的反方向更新参数 θ。这可以通过以下公式表示：
θ ← θ − α ∇ θ ​ L ( θ ) θ←θ−α∇θ​L(θ) θ←θ−α∇θ​L(θ)

Double DQN 算法基于 TD 误差进行模型训练，参数更新公式可表示为
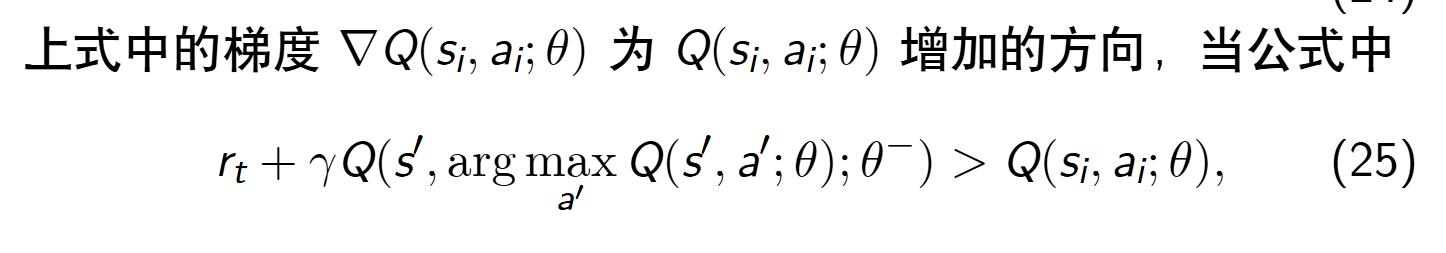
在这里插入图片描述
举例说明
在这里插入图片描述
我们最小化损失函数， Q ( s i , a i ; θ ) Q(s_i, a_i; θ) Q(si​,ai​;θ)【预测值】 必须越来越逼近 r t + γ Q ( s ′ , arg ⁡ m a x a ′ Q ( s ′ , a ′ ; θ ) ; θ − ) r_t + γQ(s′, \arg max_{a′} Q(s′, a′; θ); θ−) rt​+γQ(s′,argmaxa′​Q(s′,a′;θ);θ−)【目标值】，则参数 θ 朝着 Q ( s i , a i ; θ ) Q(s_i, a_i; θ) Q(si​,ai​;θ) 增加的方向更新。我们增加 Q ( s i , a i ; θ ) Q(s_i, a_i; θ) Q(si​,ai​;θ)，缩小 Q ( s i , a i ; θ ) Q(s_i, a_i; θ) Q(si​,ai​;θ) 与目标值 y t y_t yt​ 之间的差距。

当公式中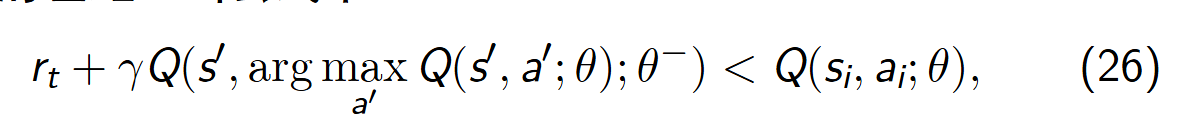
在这里插入图片描述
参数 θ 朝着 Q(si, ai; θ) 减小的方向更新。我们减小 Q(si, ai; θ)，缩小 Q(si, ai; θ) 与目标值 yt 的差距。

4.6 DQN与DDQN的结构

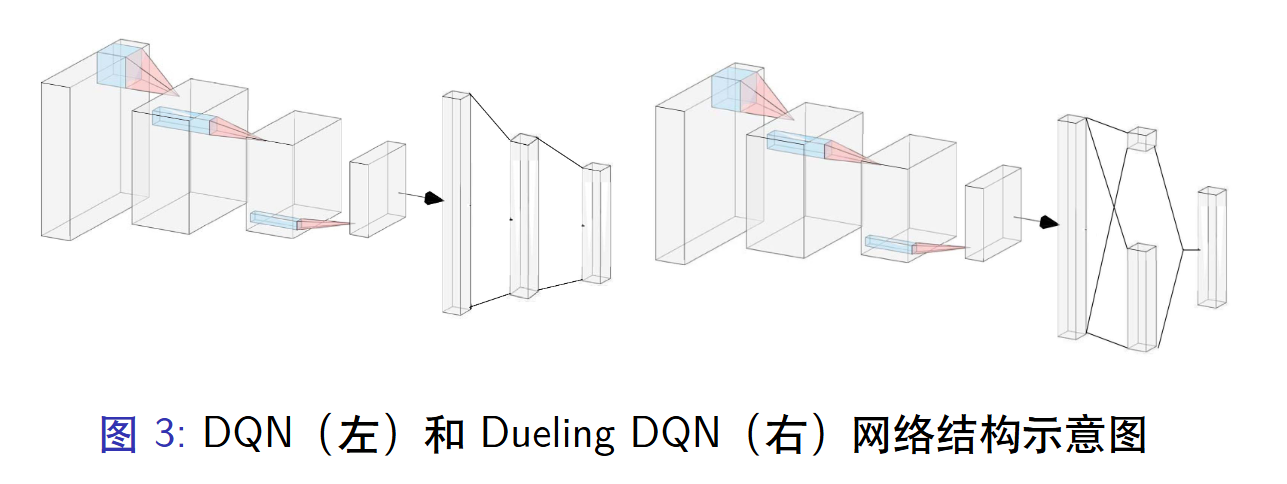
在这里插入图片描述
可以看到 DDQN中有一个模块分离的结构！

五、DDQN

4.1 核心思想

Dueling DQN 核心思想是将状态-动作值函数 Q ( s , a ; θ ) Q(s, a; θ) Q(s,a;θ) 分解成两部分，一部分是状态值函数 V ( s ; θ , β ) V(s; θ, β) V(s;θ,β)，另一部分是在状态值函数基础上选择动作 a 的优势函数 A ( s , a ; θ , α ) A(s, a; θ, α) A(s,a;θ,α)，用公式表示如下
在这里插入图片描述
在这里插入图片描述

4.2 DQN和DDQN作用于同一个案例

1.网络和环境定义
import gym
import numpy as np
import random
import torch
import torch.nn as nn
import torch.optim as optim
from collections import deque

# 定义环境
env = gym.make('CartPole-v1')
state_size = env.observation_space.shape[0]
action_size = env.action_space.n

# 定义神经网络
class DQN(nn.Module):
    def __init__(self, state_size, action_size):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(state_size, 24)
        self.fc2 = nn.Linear(24, 24)
        self.fc3 = nn.Linear(24, action_size)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        return self.fc3(x)
2. 经验回放机制
class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = deque(maxlen=capacity)

    def add(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        return random.sample(self.buffer, batch_size)
3. 智能体DQN和DDQN

DQN和DDQN的网络结构是一致的，且各种部件(如学习率，目标网络等)也是一致的。却别在于训练（评估）过程中的 “动作选择”
DQN

class DQNAgent:
    def __init__(self, state_size, action_size, gamma=0.99, learning_rate=0.001, buffer_size=10000, batch_size=64):
        self.state_size = state_size
        self.action_size = action_size
        self.gamma = gamma
        self.learning_rate = learning_rate #学习率
        self.batch_size = batch_size  
        self.epsilon = 1.0
        self.epsilon_decay = 0.995
        self.epsilon_min = 0.01
        self.memory = ReplayBuffer(buffer_size)  ##经验池
        self.model = DQN(state_size, action_size)  ##Q-network
        self.target_model = DQN(state_size, action_size) ##目标网络
        self.target_model.load_state_dict(self.model.state_dict()) ##目标网络的参数加载
        self.optimizer = optim.Adam(self.model.parameters(), lr=learning_rate)##优化器
        self.loss_fn = nn.MSELoss()

    def act(self, state):
        if random.random() < self.epsilon:
            return random.randint(0, self.action_size - 1)
        state = torch.tensor(state, dtype=torch.float32)
        q_values = self.model(state)
        return torch.argmax(q_values).item()

    def remember(self, state, action, reward, next_state, done):
        self.memory.add(state, action, reward, next_state, done)

    def train(self):
        if len(self.memory.buffer) < self.batch_size:
            return
        batch = self.memory.sample(self.batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)
        states = torch.tensor(states, dtype=torch.float32)
        actions = torch.tensor(actions, dtype=torch.int64)
        rewards = torch.tensor(rewards, dtype=torch.float32)
        next_states = torch.tensor(next_states, dtype=torch.float32)
        dones = torch.tensor(dones, dtype=torch.float32)

        
        q_values = self.model(states)  # 使用在线网络计算当前状态的Q值
    	next_q_values = self.target_model(next_states)  # 使用目标网络计算下一个状态的Q值
        q_targets = q_values.clone()

        for i in range(self.batch_size):
            if dones[i]:
                q_targets[i, actions[i]] = rewards[i]
            else:
                q_targets[i, actions[i]] = rewards[i] + self.gamma * torch.max(next_q_values[i])

        loss = self.loss_fn(q_values, q_targets)
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        if self.epsilon > self.epsilon_min:
            self.epsilon *= self.epsilon_decay

    def update_target_model(self):
        self.target_model.load_state_dict(self.model.state_dict())

DDQN


class DDQNAgent(DQNAgent):
    def __init__(self, state_size, action_size, gamma=0.99, learning_rate=0.001, buffer_size=10000, batch_size=64):
        super(DDQNAgent, self).__init__(state_size, action_size, gamma, learning_rate, buffer_size, batch_size)
		###  DDQNAgent 继承自 DQNAgent，并在 __init__ 方法中调用了父类的初始化方法，确保所有必要的属性都被正确初始化
    def train(self):
        if len(self.memory.buffer) < self.batch_size:
            return
        batch = self.memory.sample(self.batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)
        states = torch.tensor(states, dtype=torch.float32)
        actions = torch.tensor(actions, dtype=torch.int64)
        rewards = torch.tensor(rewards, dtype=torch.float32)
        next_states = torch.tensor(next_states, dtype=torch.float32)
        dones = torch.tensor(dones, dtype=torch.float32)


        q_values = self.model(states)  # 使用在线网络计算当前状态的Q值
  		next_q_values = self.model(next_states)  # 使用在线网络选择下一个状态的动作
    	next_q_values_target = self.target_model(next_states)  # 使用目标网络评估所选择动作的价值
  	  	q_targets = q_values.clone()


        for i in range(self.batch_size):
            if dones[i]:
                q_targets[i, actions[i]] = rewards[i]
            else:
                next_action = torch.argmax(next_q_values[i])
                q_targets[i, actions[i]] = rewards[i] + self.gamma * next_q_values_target[i, next_action]

        loss = self.loss_fn(q_values, q_targets)
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        if self.epsilon > self.epsilon_min:
            self.epsilon *= self.epsilon_decay

区别
两者的动作选择不是指，交互过程中的动作选择。即下面代码是相同的

def act(self, state):
    if random.random() < self.epsilon:
        return random.randint(0, self.action_size - 1)
    state = torch.tensor(state, dtype=torch.float32)
    q_values = self.model(state) ###Q-网络
    return torch.argmax(q_values).item()

DQN的目标值的确定


q_values = self.model(states)  # 使用在线网络计算当前状态的Q值
next_q_values = self.target_model(next_states)  # 使用目标网络计算下一个状态的Q值
q_targets = q_values.clone()

for i in range(self.batch_size):
    if dones[i]:
        q_targets[i, actions[i]] = rewards[i]
    else:
        next_action = torch.argmax(next_q_values[i])  ###注意这里！目标网络中的最大值！！
        q_targets[i, actions[i]] = rewards[i] + self.gamma * next_q_values_target[i, next_action]

DDQN的目标值的确定

q_values = self.model(states)  # 使用在线网络计算当前状态的Q值
next_q_values = self.model(next_states)  # 使用在线网络选择下一个状态的动作
next_q_values_target = self.target_model(next_states)  # 使用目标网络评估所选择动作的价值
q_targets = q_values.clone()


for i in range(self.batch_size):
   if dones[i]:
       q_targets[i, actions[i]] = rewards[i]
   else:
       next_action = torch.argmax(next_q_values[i]) ###注意这里！在线网络中的最大值！！
       q_targets[i, actions[i]] = rewards[i] + self.gamma * next_q_values_target[i, next_action]
4. 训练过程

经过对比，两者代码除了实例化对象名称不同外，完全相同！

训练DQN

# 训练DQN
dqn_agent = DQNAgent(state_size, action_size)
for episode in range(500):
    state = env.reset()
    done = False
    total_reward = 0
    while not done:
        action = dqn_agent.act(state)
        next_state, reward, done, _ = env.step(action)
        dqn_agent.remember(state, action, reward, next_state, done)
        state = next_state
        total_reward += reward
        dqn_agent.train()
    dqn_agent.update_target_model()
    print(f"DQN Episode: {episode}, Total Reward: {total_reward}")

训练DDQN

# 训练DDQN
ddqn_agent = DDQNAgent(state_size, action_size)
for episode in range(500):
    state = env.reset()
    done = False
    total_reward = 0
    while not done:
        action = ddqn_agent.act(state)
        next_state, reward, done, _ = env.step(action)
        ddqn_agent.remember(state, action, reward, next_state, done)
        state = next_state
        total_reward += reward
        ddqn_agent.train()
    ddqn_agent.update_target_model()
    print(f"DDQN Episode: {episode}, Total Reward: {total_reward}")

附录一：DQN案例代码

A.1 智能体

目标网络的引入：
    self.target_network 是目标网络，它的参数定期从在线网络（self.q_network）复制过来。
    在 __init__ 方法中，目标网络的参数初始化为在线网络的参数。
目标网络的更新：
    在 replay 方法中，使用目标网络计算下一个状态的 Q 值（next_q_values）。
    每次调用 replay 方法时，更新计数器 self.update_count 增加 1。
    当 self.update_count 达到目标网络更新频率（self.target_update_frequency）时，将在线网络的参数复制到目标网络。
目标网络的作用：
    目标网络的参数更新频率较低，这使得目标值（q_target）相对稳定，从而减少了目标值和预测值之间的相关性，提高了训练的稳定性。

class DQN_Agent:
    def __init__(self, env, lr=0.001, gamma=0.99, epsilon=1.0, epsilon_decay=0.995, min_epsilon=0.01, buffer_size=10000, batch_size=32, target_update_frequency=1000):
        self.env = env
        self.lr = lr
        self.gamma = gamma
        self.epsilon = epsilon
        self.epsilon_decay = epsilon_decay
        self.min_epsilon = min_epsilon
        self.buffer_size = buffer_size
        self.batch_size = batch_size
        self.replay_buffer = deque(maxlen=buffer_size)
        self.state_dim = (1, 8, 8)  # 输入维度：1 个通道，8x8 的图像
        self.action_dim = 4  # 动作维度 (上, 下, 左, 右)
        self.q_network = DQN(self.state_dim[0], self.action_dim)  # 在线网络
        self.target_network = DQN(self.state_dim[0], self.action_dim)  # 目标网络
        self.target_network.load_state_dict(self.q_network.state_dict())  # 初始化目标网络
        self.target_network.eval()  # 设置为目标网络模式
        self.optimizer = optim.Adam(self.q_network.parameters(), lr=self.lr)
        self.loss_fn = nn.MSELoss()
        self.target_update_frequency = target_update_frequency  # 目标网络更新频率
        self.update_count = 0  # 更新计数器

    def choose_action(self, state):
        if random.random() < self.epsilon:
            return random.randint(0, self.action_dim - 1)
        else:
            state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)  # 添加批次维度
            q_values = self.q_network(state)
            return torch.argmax(q_values).item()

    def store_experience(self, state, action, reward, next_state, done):
        self.replay_buffer.append((state, action, reward, next_state, done))

    def train(self, episodes):
        for episode in range(episodes):
            state = self.env.reset()
            done = False
            while not done:
                action = self.choose_action(state)
                next_state, reward, done = self.env.step(action)
                self.store_experience(state, action, reward, next_state, done)
                state = next_state

                if len(self.replay_buffer) > self.batch_size:
                    self.replay()

            self.epsilon = max(self.min_epsilon, self.epsilon * self.epsilon_decay)
            if (episode + 1) % 100 == 0:
                print(f"Episode {episode + 1}/{episodes} completed, epsilon: {self.epsilon:.4f}")

    def replay(self):
        batch = random.sample(self.replay_buffer, self.batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)

        states = torch.tensor(states, dtype=torch.float32)
        actions = torch.tensor(actions, dtype=torch.int64)
        rewards = torch.tensor(rewards, dtype=torch.float32)
        next_states = torch.tensor(next_states, dtype=torch.float32)
        dones = torch.tensor(dones, dtype=torch.float32)

        q_values = self.q_network(states)  # 使用在线网络计算 Q 值
        next_q_values = self.target_network(next_states)  # 使用目标网络计算下一个状态的 Q 值
        q_target = q_values.clone()

        for i in range(self.batch_size):
            if dones[i] == 1:
                q_target[i, actions[i]] = rewards[i]
            else:
                q_target[i, actions[i]] = rewards[i] + self.gamma * torch.max(next_q_values[i])

        loss = self.loss_fn(q_values, q_target)
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        # 更新目标网络
        self.update_count += 1
        if self.update_count % self.target_update_frequency == 0:
            self.target_network.load_state_dict(self.q_network.state_dict())

    def test(self):
        state = self.env.reset()
        done = False
        path = [state]
        while not done:
            state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)  # 添加批次维度
            q_values = self.q_network(state)
            action = torch.argmax(q_values).item()
            state, _, done = self.env.step(action)
            path.append(state)
        print("Path taken:", path)

A.2 网络结构

输入层：
    输入是一个 8x8 的灰度图像，通道数为 1。
    输入维度为 (batch_size, 1, 8, 8)。
第一层：卷积层：
    使用 nn.Conv2d，输入通道为 1，输出通道为 16，卷积核大小为 3x3，步长为 1，填充为 1。
    输出维度为 (batch_size, 16, 8, 8)。
    应用 ReLU 激活函数。
第二层：全连接层：
    将卷积层的输出展平为一维张量，维度为 (batch_size, 16 * 8 * 8)。
    使用 nn.Linear，输入维度为 16 * 8 * 8，输出维度为 128。
    应用 ReLU 激活函数。
第三层：全连接层：
    使用 nn.Linear，输入维度为 128，输出维度为 128。
    应用 ReLU 激活函数。
输出层：
    使用 nn.Linear，输入维度为 128，输出维度为 output_dim（动作数量，这里是 4）。
    输出层不使用激活函数，直接输出 Q 值。

class DQN(nn.Module):
    def __init__(self, input_channels, output_dim):
        super(DQN, self).__init__()
        # 第一层：卷积层
        self.conv1 = nn.Conv2d(input_channels, 16, kernel_size=3, stride=1, padding=1)
        # 第二层：全连接层
        self.fc1 = nn.Linear(16 * 8 * 8, 128)  # 将卷积层的输出展平
        # 第三层：全连接层
        self.fc2 = nn.Linear(128, 128)
        # 第四层：输出层
        self.fc3 = nn.Linear(128, output_dim)
        self.initialize_weights()

    def forward(self, x):
        x = torch.relu(self.conv1(x))  # 第一层卷积后应用 ReLU
        x = x.view(x.size(0), -1)  # 展平
        x = torch.relu(self.fc1(x))  # 第一层全连接后应用 ReLU
        x = torch.relu(self.fc2(x))  # 第二层全连接后应用 ReLU
        x = self.fc3(x)  # 输出层
        return x

    def initialize_weights(self):
        # 使用高斯分布初始化权重
        for layer in self.modules():
            if isinstance(layer, nn.Conv2d) or isinstance(layer, nn.Linear):
                nn.init.normal_(layer.weight, mean=0.0, std=0.1)  # 高斯分布，均值为0，标准差为0.1
                if layer.bias is not None:
                    nn.init.constant_(layer.bias, 0.0)  # 偏置初始化为0

A.3 环境

环境结构说明：

网格世界：
    网格世界是一个 8x8 的网格，智能体可以在其中向上、下、左、右移动。
    智能体的目标是从起点 start 到达终点 goal。
状态表示：
    智能体的状态是一个二维坐标 (x, y)。
    状态被转换为一个 8x8 的灰度图像，智能体的位置用 1 表示，其余位置用 0 表示。
奖励机制：
    每一步的奖励为 -1。
    到达目标位置的奖励为 100。
输入维度：
    环境的输入是一个 8x8 的灰度图像，通道数为 1。
    输入维度为 (1, 8, 8)。

class GridWorld:
    def __init__(self, rows, cols, start, goal):
        self.rows = rows
        self.cols = cols
        self.start = start
        self.goal = goal
        self.state = start

    def reset(self):
        self.state = self.start
        return self.state_to_image(self.state)

    def step(self, action):
        x, y = self.state
        if action == 0:  # 上
            x = max(x - 1, 0)
        elif action == 1:  # 下
            x = min(x + 1, self.rows - 1)
        elif action == 2:  # 左
            y = max(y - 1, 0)
        elif action == 3:  # 右
            y = min(y + 1, self.cols - 1)
        
        self.state = (x, y)
        reward = -1  # 每一步的惩罚
        done = self.state == self.goal
        if done:
            reward = 100  # 到达目标的奖励
        return self.state_to_image(self.state), reward, done

    def state_to_image(self, state):
        # 将状态转换为 8x8 的灰度图像
        img = np.zeros((8, 8), dtype=np.float32)
        img[state[0], state[1]] = 1.0  # 将智能体的位置设置为 1
        return img
Logo
火山引擎 ADG 社区

火山引擎开发者社区是火山引擎打造的AI技术生态平台，聚焦Agent与大模型开发，提供豆包系列模型（图像/视频/视觉）、智能分析与会话工具，并配套评测集、动手实验室及行业案例库。社区通过技术沙龙、挑战赛等活动促进开发者成长，新用户可领50万Tokens权益，助力构建智能应用。

更多推荐

Chess用户界面设计：Tailwind CSS样式系统和组件库

GitHub推荐项目精选中的ch/chess是一个类似chess.com的多人在线象棋平台，它采用现代化的前端技术栈构建，尤其在用户界面设计上通过Tailwind CSS样式系统和组件库实现了优雅且功能丰富的交互体验。本文将深入探讨该项目如何利用Tailwind CSS打造一致的设计语言和高效的组件系统，为象棋爱好者提供沉浸式的游戏界面。## 🎨 Tailwind CSS样式系统：构建统一视

avatar 火山引擎 ADG 社区

终极指南：GPT-Engineer如何通过AI自动发现代码问题并提升质量

GPT-Engineer是一款强大的AI驱动代码工具，它能帮助开发者自动检测潜在代码问题、优化代码质量，让编程效率提升3倍以上。无论是新手还是资深开发者，都能通过这款工具轻松发现代码中的隐藏缺陷，减少调试时间，释放更多精力在创造性工作上。## 一键发现代码问题：GPT-Engineer的AI审查魔力GPT-Engineer的核心能力在于其内置的智能代码分析系统。通过集成Python代码格式

avatar 火山引擎 ADG 社区

SatDump中的纠错编码技术：从RS码到Turbo码的完整实现指南

在卫星数据传输过程中，信号往往会受到各种干扰，导致数据错误。SatDump作为一款通用卫星数据处理软件，集成了多种先进的纠错编码技术，确保从卫星接收到的数据能够准确解码。本文将深入解析SatDump中从Reed-Solomon（RS）码到Turbo码的实现细节，帮助读者理解这些技术如何保障卫星通信的可靠性。## 为什么纠错编码对卫星数据至关重要？卫星与地面站之间的通信链路面临着空间辐射、大

avatar 火山引擎 ADG 社区