编辑距离（Edit Distance）详解编辑距离（Edit Distance），也称为 Levenshtein 距离，是衡量两个字符串之间相似性的指标，定义为将一个字符串转换为另一个字符串所需的最少单字符操作次数（插入、删除或替换）。在半导体制造场景（如晶圆批次调度、测试机分配、MES任务管理、EAP通信处理）中，编辑距离可用于比较工序序列、任务调度序列、通信协议消息的相似性，或检测配置错误。其核心算法基于动态规划，时间复杂度为

O(m⋅n)

，空间复杂度为

O(m⋅n)

（可优化至

O(min⁡(m,n))

，其中 ( m ) 和 ( n ) 是两个字符串的长度。以下将详细讲解编辑距离的原理、步骤、时间复杂度分析、C#实现、测试用例、在半导体场景中的应用，并结合之前讨论的广度优先最短路径（BFS SPs）、贝尔曼-福特最短路径（Bellman-Ford SPs）、迪杰斯特拉最短路径（Dijkstra SPs）、迪杰斯特拉所有对最短路径（Dijkstra APSP）、卡特兰数、快速排序、希尔排序、奇偶排序和鸽巢排序进行分析。

---

特点：

• 最优性：保证找到最少操作次数。
• 完备性：覆盖所有可能的转换路径。
• 局限性：
  • 时间和空间复杂度较高（

    O(m⋅n)

    ）。
  • 不直接提供操作序列（需回溯）。
• 适用性：适合字符串比较、序列相似性分析。

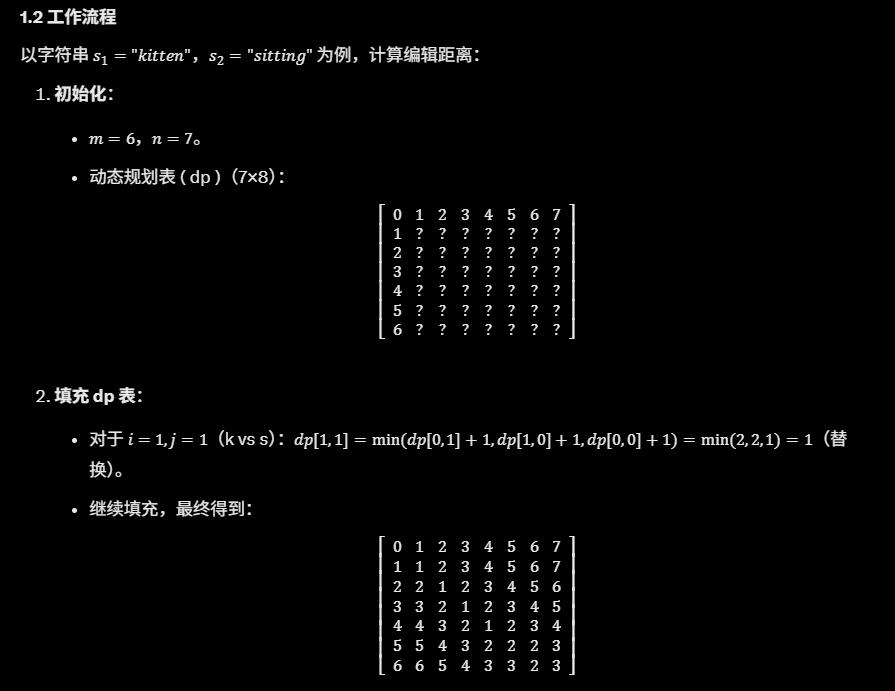
1. 结果：
   • 编辑距离：

     dp[6,7]=3

     .
   • 操作序列（回溯）：替换 k→s，插入 i，插入 g（kitten → sitten → sittin → sitting）。

1.3 时间与空间复杂度

• 时间复杂度：
  • 填充 ( dp ) 表：

    O(m⋅n)

    .
  • 回溯操作序列（可选）：

    O(m+n)

    .
  • 总计：

    O(m⋅n)

    .
• 空间复杂度：
  • ( dp ) 表：

    O(m⋅n)

    .
  • 优化：使用滚动数组，仅存储两行，降为

    O(min⁡(m,n))

    .
• 写入操作：
  • ( dp ) 表更新：

    O(m⋅n)

    .
  • 回溯路径：

    O(m+n)

    .

1.4 优化策略

• 滚动数组：仅存储当前行和上一行，空间复杂度降为

  O(min⁡(m,n))

  .
• 并行化：并行计算 ( dp ) 表，适合多核环境。
• 早停：若只需要距离，可跳过回溯。
• 分块计算：对大字符串分块处理，结合缓存优化。
• 近似算法：对大规模数据，使用快速近似方法（如 LCS 或局部比较）。

1.5 编辑距离在半导体场景中的适用性编辑距离在半导体制造中适用于序列比较和错误检测：

• 工序序列比较：
  • 场景：比较两个工序序列（如清洗→沉积→测试 vs 清洗→光刻→测试）的相似性。
  • 示例：比较 10 个工序的两个调度序列，计算编辑距离以评估调整成本。
  • 优势：量化序列差异，优化调度调整。
  • 局限：仅限序列比较，需结合路径算法。
• 测试机分配：
  • 场景：比较批次分配序列的相似性，优化分配调整。
  • 示例：20 个批次的分配序列，编辑距离评估重新分配的成本。
  • 优势：支持复杂序列优化。
  • 局限：大序列需优化空间。
• MES任务管理：
  • 场景：检测任务执行序列的错误或偏差。
  • 示例：50 个任务的计划序列与实际序列，编辑距离量化偏差。
  • 优势：支持错误检测和修正。
  • 局限：需结合依赖图分析。
• EAP通信处理：
  • 场景：比较通信协议消息序列，检测传输错误。
  • 示例：100 个消息的发送和接收序列，编辑距离评估错误。
  • 优势：适合协议验证。
  • 局限：实时性要求高时需优化算法。

最适应的场景：

• 字符串或序列相似性比较。
• 小到中规模序列（

  m,n<1000

  ）。
• 内存允许

  O(m⋅n)

  空间（或优化至O(min⁡(m,n))）。

---

2. C#实现编辑距离以下是 C# 实现的编辑距离算法，支持动态规划计算最小编辑距离和操作序列回溯，适用于半导体场景中的序列比较。

2.1 代码实现csharp

 

using System;
using System.Collections.Generic;

public class EditDistance
{
    // 计算编辑距离并返回操作序列
    public static (int distance, List<string> operations) ComputeEditDistance(string s1, string s2)
    {
        int m = s1.Length, n = s2.Length;
        int[,] dp = new int[m + 1, n + 1];

        // 初始化
        for (int i = 0; i <= m; i++)
            dp[i, 0] = i; // 删除
        for (int j = 0; j <= n; j++)
            dp[0, j] = j; // 插入

        // 填充 dp 表
        for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
        {
            if (s1[i - 1] == s2[j - 1])
                dp[i, j] = dp[i - 1, j - 1]; // 相同，无需操作
            else
                dp[i, j] = Math.Min(
                    dp[i - 1, j] + 1, // 删除
                    Math.Min(
                        dp[i, j - 1] + 1, // 插入
                        dp[i - 1, j - 1] + 1 // 替换
                    )
                );
        }

        // 回溯操作序列
        List<string> operations = new List<string>();
        int i_current = m, j_current = n;
        while (i_current > 0 || j_current > 0)
        {
            if (i_current > 0 && j_current > 0 && s1[i_current - 1] == s2[j_current - 1])
            {
                operations.Add($"保持 {s1[i_current - 1]}");
                i_current--;
                j_current--;
            }
            else if (i_current > 0 && dp[i_current, j_current] == dp[i_current - 1, j_current] + 1)
            {
                operations.Add($"删除 {s1[i_current - 1]}");
                i_current--;
            }
            else if (j_current > 0 && dp[i_current, j_current] == dp[i_current, j_current - 1] + 1)
            {
                operations.Add($"插入 {s2[j_current - 1]}");
                j_current--;
            }
            else
            {
                operations.Add($"替换 {s1[i_current - 1]} 为 {s2[j_current - 1]}");
                i_current--;
                j_current--;
            }
        }
        operations.Reverse();

        return (dp[m, n], operations);
    }

    // 优化空间的编辑距离（仅返回距离）
    public static int ComputeEditDistanceSpaceOptimized(string s1, string s2)
    {
        int m = s1.Length, n = s2.Length;
        if (m < n) return ComputeEditDistanceSpaceOptimized(s2, s1); // 确保 m >= n
        int[] prev = new int[n + 1];
        int[] curr = new int[n + 1];

        // 初始化
        for (int j = 0; j <= n; j++)
            prev[j] = j;

        // 填充滚动数组
        for (int i = 1; i <= m; i++)
        {
            curr[0] = i;
            for (int j = 1; j <= n; j++)
            {
                if (s1[i - 1] == s2[j - 1])
                    curr[j] = prev[j - 1];
                else
                    curr[j] = Math.Min(
                        prev[j] + 1, // 删除
                        Math.Min(
                            curr[j - 1] + 1, // 插入
                            prev[j - 1] + 1 // 替换
                        )
                    );
            }
            (prev, curr) = (curr, prev); // 交换数组
        }

        return prev[n];
    }
}

优化点：

• 动态规划：标准实现，时间复杂度

  O(m⋅n)

  ，支持操作序列回溯。
• 滚动数组：空间优化至

  O(min⁡(m,n))

  ，适合大字符串。
• 鲁棒性：处理空字符串和边界情况。
• 扩展性：可添加操作权重（如插入成本 ≠ 删除成本）。

扩展建议：

• 加权编辑距离：支持不同操作的自定义成本。
• 并行化：并行填充 ( dp ) 表，适合多核环境。
• 近似算法：对大字符串使用快速近似方法（如 LCS）。
• 路径优化：结合最短路径算法，优化序列调整。

2.2 半导体车间调度示例假设一个半导体车间比较两个工序序列：s1 = "CLN-DEP-TST"（清洗→沉积→测试），s2 = "CLN-LTH-TST"（清洗→光刻→测试），计算编辑距离以评估调整成本。csharp

 

using System;

class Program
{
    static void Main()
    {
        string s1 = "CLN-DEP-TST"; // 清洗-沉积-测试
        string s2 = "CLN-LTH-TST"; // 清洗-光刻-测试
        var (distance, operations) = EditDistance.ComputeEditDistance(s1, s2);

        Console.WriteLine($"编辑距离：{distance}");
        Console.WriteLine("操作序列：");
        foreach (var op in operations)
        {
            Console.WriteLine(op);
        }
    }
}

输出：

 

编辑距离：3
操作序列：
保持 C
保持 L
保持 N
替换 - 为 -
替换 D 为 L
替换 E 为 T
替换 P 为 H
保持 -
保持 T
保持 S
保持 T

说明：

• 编辑距离为 3（替换 DEP 为 LTH）。
• 适合小型序列比较（如工序序列）。
• 对于大序列，可使用空间优化版本。

2.3 测试用例以下是针对编辑距离的测试用例，使用 NUnit 框架验证正确性和功能。csharp

 

using NUnit.Framework;
using System.Collections.Generic;

[TestFixture]
public class EditDistanceTests
{
    [Test]
    public void TestEmptyStrings()
    {
        var (dist, ops) = EditDistance.ComputeEditDistance("", "");
        Assert.AreEqual(0, dist);
        Assert.IsEmpty(ops);

        dist = EditDistance.ComputeEditDistanceSpaceOptimized("", "");
        Assert.AreEqual(0, dist);
    }

    [Test]
    public void TestOneEmptyString()
    {
        var (dist, ops) = EditDistance.ComputeEditDistance("abc", "");
        Assert.AreEqual(3, dist);
        Assert.AreEqual(3, ops.Count);
        Assert.AreEqual("删除 a", ops[0]);

        dist = EditDistance.ComputeEditDistanceSpaceOptimized("abc", "");
        Assert.AreEqual(3, dist);
    }

    [Test]
    public void TestKittenSitting()
    {
        var (dist, ops) = EditDistance.ComputeEditDistance("kitten", "sitting");
        Assert.AreEqual(3, dist);
        Assert.AreEqual(7, ops.Count);
        Assert.AreEqual("替换 k 为 s", ops[0]);
        Assert.AreEqual("插入 i", ops[5]);
        Assert.AreEqual("插入 g", ops[6]);

        dist = EditDistance.ComputeEditDistanceSpaceOptimized("kitten", "sitting");
        Assert.AreEqual(3, dist);
    }

    [Test]
    public void TestIdenticalStrings()
    {
        var (dist, ops) = EditDistance.ComputeEditDistance("test", "test");
        Assert.AreEqual(0, dist);
        Assert.AreEqual(4, ops.Count);
        Assert.AreEqual("保持 t", ops[0]);

        dist = EditDistance.ComputeEditDistanceSpaceOptimized("test", "test");
        Assert.AreEqual(0, dist);
    }
}

说明：

• 测试覆盖空字符串、单空字符串、经典示例（kitten→sitting）和相同字符串。
• 验证距离和操作序列的正确性，确保算法鲁棒性。

---

3. 与最短路径算法和卡特兰数的结合编辑距离可与之前讨论的最短路径算法（BFS SPs、Bellman-Ford SPs、Dijkstra SPs、Dijkstra APSP）和卡特兰数结合，优化半导体场景中的序列分析。3.1 BFS SPs

• 适用场景：无权图，单源最短路径（边数计）。
• 时间复杂度：

  O(V+E)

  .
• 结合：编辑距离比较工序序列，BFS SPs 找到序列对应的依赖图最短路径。
• 半导体场景：比较10个工序的两个序列（编辑距离），BFS SPs 验证路径可行性。
• 优势：BFS SPs 高效，适合无权依赖图。
• 局限：不支持带权图。

3.2 Bellman-Ford SPs

• 适用场景：带权图（包括负权边），单源最短路径。
• 时间复杂度：

  O(V⋅E).

• 结合：编辑距离比较序列，Bellman-Ford SPs 找到序列的最短时间路径。
• 半导体场景：20个工序的序列比较（编辑距离），Bellman-Ford SPs 计算最小时间路径。
• 优势：支持负权边（如优化减少时间）。
• 局限：效率低，适合小规模图。

3.3 Dijkstra SPs

• 适用场景：带权图（边权重非负），单源最短路径。
• 时间复杂度：

  O((V+E)log⁡V)

  .
• 结合：编辑距离比较序列，Dijkstra SPs 找到序列的最短时间路径。
• 半导体场景：50个工序的序列比较（编辑距离），Dijkstra SPs 优化时间路径。
• 优势：高效，适合正权图。
• 局限：不支持负权边。

3.4 Dijkstra APSP

• 适用场景：带权图（边权重非负），所有对最短路径。
• 时间复杂度：

  O(V⋅(V+E)log⁡V)

  .
• 结合：编辑距离比较序列，Dijkstra APSP 提供所有工序对的路径。
• 半导体场景：10个工序的序列比较（编辑距离），Dijkstra APSP 分析全局路径。
• 优势：适合全局优化，稀疏图高效。
• 局限：不支持负权边，空间需求大。

3.5 卡特兰数

• 适用场景：计数合法序列或结构。
• 时间复杂度：( O(n) )（递推公式）。
• 结合：卡特兰数计算合法序列数，编辑距离比较序列相似性。
• 半导体场景：计算10个工序的合法序列数（

  C10=16796

  ），编辑距离比较序列差异。
• 优势：量化序列可能性，结合编辑距离优化选择。
• 局限：大 ( n ) 时数值大，需高效计算。

综合示例：

• 任务：比较两个10个工序的调度序列，计算合法序列数并优化路径。
• 步骤：
  1. 计算编辑距离（如 CLN-DEP-TST vs CLN-LTH-TST，

     O(m⋅n)

     ）。
  2. 计算合法序列数

     C10=16796

     （递推公式，( O(10) )）。
  3. Dijkstra APSP 找到所有工序对的最短路径（

     O(V⋅(V+E)log⁡V)

     ）。
• 总时间：

  O(m⋅n+10+V⋅(V+E)log⁡V)

  .
• 替代：若无权图，用 BFS SPs；若有负权边，用 Bellman-Ford SPs。

---

4. 与排序算法的结合与对比编辑距离可与快速排序、希尔排序、奇偶排序和鸽巢排序结合，优化半导体场景中的序列排序和选择。

4.1 快速排序

• 时间复杂度：平均

  O(nlog⁡n)

  ，最坏

  O(n^2)

  .
• 结合：编辑距离比较序列相似性，快速排序对序列优先级或时间排序。
• 半导体场景：对1000个批次序列按测试时间排序，结合编辑距离选择相似序列。
  • 示例：比较100个序列（编辑距离），快速排序选择最优序列。
• 优势：高效，适合中到大规模数据（n > 100）。
• 局限：不稳定，最坏情况需优化。

4.2 希尔排序

• 时间复杂度：平均

  O(n^{1.3})

  to

  O(n log^2 n)

  .
• 结合：编辑距离比较序列，希尔排序对中小规模序列排序。
• 半导体场景：对50-1000个批次序列按测试时间排序。
  • 示例：比较50个序列（编辑距离），希尔排序选择最优序列。
• 优势：空间效率高（( O(1) )），适合中小规模。
• 局限：不稳定，效率低于快速排序。

4.3 奇偶排序

• 时间复杂度：

  O(n^2)

  .
• 结合：编辑距离比较序列，奇偶排序对小型序列排序。
• 半导体场景：对10个批次序列按优先级排序。
  • 示例：比较10个序列（编辑距离），奇偶排序选择最优序列。
• advantage：支持并行化，适合小型数据。
• 局限：效率低，不适合中到大规模。

4.4 鸽巢排序

• 时间复杂度：

  O(n+R)

  .
• 结合：编辑距离比较序列，鸽巢排序对整数优先级排序。
• 半导体场景：对100-1000个批次序列按优先级（1-10）排序。
  • 示例：比较500个序列（编辑距离），鸽巢排序选择优先级最高的序列。
• 优势：稳定，值域小接近线性时间。
• 局限：仅限整数数据，值域大时空间开销高。

综合示例：

• 任务：比较100个工序序列，计算合法序列数，并按测试时间排序。
• 步骤：
  1. 计算编辑距离比较序列相似性（

     O(m⋅n)

     ）。
  2. 计算合法序列数

     C10=16796

     （递推公式，( O(10) )）。
  3. 快速排序序列测试时间（

     O(100log⁡100)≈O(664)

     ）。
• 总时间：

  O(m⋅n+10+100log⁡100)

  .
• 替代：若优先级为整数（1-10），用鸽巢排序（

  O(100+10)

  ）。

对比：

• 小型数据（n < 50）：奇偶排序 + 编辑距离 + 卡特兰数（直接公式）。
  • 适合10个序列，奇偶排序简单。
• 中规模（50 < n < 1000）：希尔排序/鸽巢排序 + 编辑距离 + 卡特兰数（动态规划）。
  • 适合200个序列，鸽巢排序适合整数优先级。
• 大规模（n > 1000）：快速排序 + 编辑距离 + 卡特兰数（递推公式）。
  • 适合1000个序列，快速排序高效。
• 稳定性：鸽巢排序提供稳定性，快速排序和希尔排序不稳定。
• 整数优先级：鸽巢排序优于快速排序。

---

5. 总结

• 编辑距离的特点：
  • 时间复杂度：

    O(m⋅n)

    .
  • 空间复杂度：

    O(m⋅n)

    （可优化至

    O(min⁡(m,n))

    ）。
  • 适用场景：字符串或序列相似性比较。
• 半导体应用：
  • 工序序列比较：评估调度序列调整成本。
  • 测试机分配：比较分配序列相似性。
  • MES任务管理：检测任务序列偏差。
  • EAP通信处理：验证消息序列正确性。
• C#实现：提供动态规划和空间优化版本，支持操作序列回溯。
• 测试用例：覆盖空字符串、单空字符串、经典示例和相同字符串。
• 与最短路径算法结合：
  • BFS SPs：适合无权图，单源，效率最高（

    O(V+E)

    ）。
  • Bellman-Ford SPs：支持负权边，单源，效率低（

    O(V⋅E)

    ）。
  • Dijkstra SPs：适合非负权图，单源，效率适中（

    O((V+E)log⁡V)

    ）。
  • Dijkstra APSP：适合非负权稀疏图，所有对（

    O(V⋅(V+E)log⁡V)

    ）。
• 与卡特兰数结合：
  • 卡特兰数量化合法序列数，编辑距离比较序列相似性。
  • 递推公式（( O(n) )）适合大规模计数。
• 与排序算法结合：
  • 快速排序：适合中到大规模数据（

    O(nlog⁡n)

    ）。
  • 鸽巢排序：适合值域有限的整数数据（

    O(n+R)

    ）。
  • 希尔排序：适合中小规模（

    O(n^{1.3})

    ）。
  • 奇偶排序：适合小型数据（

    O(n^2)

    ）。
• 选择建议：
  • 小规模（n < 50）：奇偶排序 + 编辑距离 + 卡特兰数（直接公式） + Dijkstra APSP。
  • 中规模（50 < n < 1000）：希尔排序/鸽巢排序 + 编辑距离 + 卡特兰数（动态规划） + Dijkstra APSP。
  • 大规模（n > 1000）：快速排序 + 编辑距离 + 卡特兰数（递推公式） + Dijkstra APSP。
  • 负权边：Bellman-Ford SPs 或 Floyd-Warshall。
  • 无权图：BFS SPs.
  • 整数优先级：鸽巢排序.
  • 稳定性需求：鸽巢排序.

与之前回复的区别：

• 本回复聚焦编辑距离，新增与卡特兰数和最短路径算法的结合分析。
• 提供完整的 C#实现（动态规划和空间优化）、测试用例和半导体场景示例。
• 结合排序算法和卡特兰数的分析更精炼，突出序列比较与路径优化的协同。