（一）实验目的与背景

        基于kaggle上的房屋价格数据集，通过XGBoost回归构建一个能够准确预测房屋价格的模型。

        房屋价格数据集包含"train.csv"和"test.csv"两个数据集，分别包含1460和1459条记录。训练集包含81列（80个特征+1个目标变量SalePrice），测试集包含80个特征列。

        XGBoost回归原理为通过迭代添加树模型，结合梯度提升和二阶泰勒展开优化目标函数，并利用正则化和高效算法提升性能，适用于回归/分类任务。

（二）实验过程

        数据导入与探索：加载房屋价格数据集并进行初步探索。

        数据预处理：

1. 合并训练集和测试集进行统一处理

2. 处理缺失值：数值列用中位数填充分类列用'None'填充并转换为类别类型

3. 特征工程：创建新特征 “TotalSF”（总平方英尺）与 “Age”（房屋年龄）

4. 处理偏态数值特征：对偏度大于0.75的数值特征进行对数转换

5. 对分类特征进行独热编码

6. 对目标变量进行对数转换

7. 将数据集分割回训练集和测试集（按初始比例分割）。

        模型训练：初始化XGBoost回归模型并在训练集上拟合模型。

        模型调优：使用网格搜索进行超参数调优

        模型评估：进行交叉验证评估模型，并进行模型特征重要性可视化

（三）代码实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import KFold, cross_val_score, GridSearchCV
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
import xgboost as xgb

#（1）数据加载
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')

#（2）数据探索
print("训练集维度:", train.shape)
print("测试集维度:", test.shape)
print("\n训练集前5行:")
print(train.head())
print("\n数据描述:")
print(train.describe())

# 可视化目标变量分布
plt.figure(figsize=(10, 6))
sns.histplot(train['SalePrice'], kde=True)
plt.title('SalePrice Distribution')
plt.show()

#（3）数据预处理
def preprocess_data(train_df, test_df):
    # 分离目标变量和ID
    target = train_df['SalePrice']
    train_ids = train_df['Id']
    test_ids = test_df['Id']
    
    # 合并数据集进行统一处理
    combined = pd.concat([train_df.drop(['Id', 'SalePrice'], axis=1), 
                         test_df.drop('Id', axis=1)], axis=0)
    
    # 处理缺失值
    num_cols = combined.select_dtypes(include=np.number).columns
    combined[num_cols] = combined[num_cols].fillna(combined[num_cols].median())
    
    # 分类列用'None'填充并转换类型
    cat_cols = combined.select_dtypes(exclude=np.number).columns
    combined[cat_cols] = combined[cat_cols].fillna('None').astype('category')
    
    # 特征工程
    combined['TotalSF'] = combined['TotalBsmtSF'] + combined['1stFlrSF'] + combined['2ndFlrSF']
    combined['Age'] = combined['YrSold'] - combined['YearBuilt']
    
    # 处理偏态数值特征
    skewed_cols = combined[num_cols].apply(lambda x: x.skew())
    skewed_cols = skewed_cols[skewed_cols > 0.75].index
    combined[skewed_cols] = np.log1p(combined[skewed_cols])
    
    # 分割回训练集和测试集
    train_processed = combined.iloc[:len(train_df)]
    test_processed = combined.iloc[len(train_df):]
    
    return train_processed, test_processed, target, test_ids

# 执行预处理
train_processed, test_processed, target, test_ids = preprocess_data(train, test)

# 分类特征编码
encoder = ColumnTransformer(
    [('onehot', OneHotEncoder(handle_unknown='ignore'), 
      train_processed.select_dtypes(include='category').columns)],
    remainder='passthrough'
)

X_train = encoder.fit_transform(train_processed)
X_test = encoder.transform(test_processed)

# 目标变量对数转换
y_train = np.log1p(target)

# （4）模型训练与评估
model = xgb.XGBRegressor(random_state=7, n_jobs=-1)

# 初始模型交叉验证
kf = KFold(n_splits=5, shuffle=True, random_state=7)
scores = -cross_val_score(model, X_train, y_train, 
                         cv=kf, 
                         scoring='neg_mean_squared_error')
rmse_scores = np.sqrt(scores)
print(f"Cross-validation RMSE: {np.mean(rmse_scores):.4f} (±{np.std(rmse_scores):.4f})")

# 超参数调优
params = {
    'n_estimators': [500, 1000],
    'learning_rate': [0.01, 0.05],
    'max_depth': [3, 4],
    'subsample': [0.8, 0.9]
}

grid_search = GridSearchCV(model, param_grid=params, 
                          scoring='neg_mean_squared_error',
                          cv=3, verbose=2, n_jobs=-1)
grid_search.fit(X_train, y_train)

best_model = grid_search.best_estimator_
print("最佳参数:", grid_search.best_params_)

# 最终模型交叉验证
kf = KFold(n_splits=5, shuffle=True, random_state=7)
scores = -cross_val_score(best_model, X_train, y_train, 
                         cv=kf, 
                         scoring='neg_mean_squared_error')
rmse_scores = np.sqrt(scores)
print(f"Cross-validation RMSE: {np.mean(rmse_scores):.4f} (±{np.std(rmse_scores):.4f})")

# 最终模型预测
final_predictions = np.expm1(best_model.predict(X_test))

# 生成提交文件
submission = pd.DataFrame({'Id': test_ids, 'SalePrice': final_predictions})
submission.to_csv('submission.csv', index=False)
print("提交文件已生成！")

# 特征重要性可视化
feature_importance = pd.DataFrame({
    'feature': encoder.get_feature_names_out(),
    'importance': best_model.feature_importances_
}).sort_values('importance', ascending=False).head(20)

plt.figure(figsize=(12, 8))
sns.barplot(x='importance', y='feature', data=feature_importance)
plt.title('Top 20 Feature Importance')
plt.show()

（四）实验结果

        1.数据探索

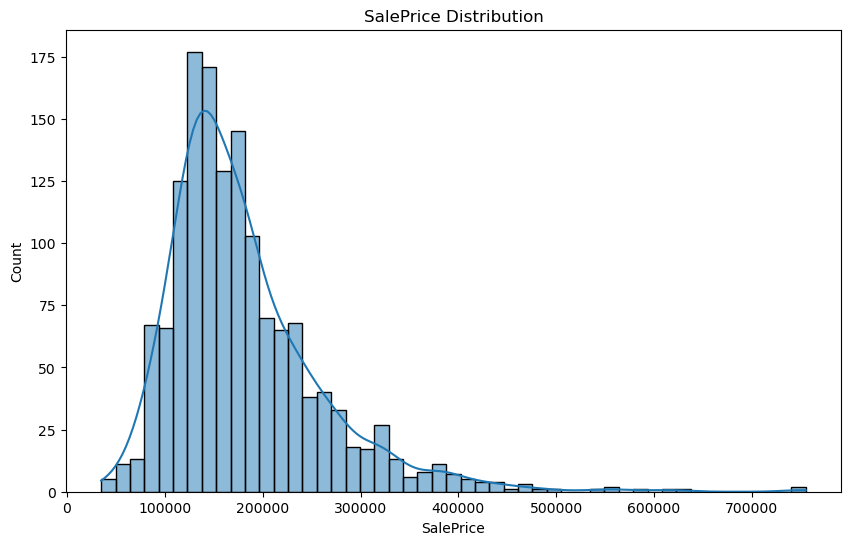
        可以看出，房价数据总体分布在100000-300000之间，另有部分样本的房价达到500000及以上；因为构建的模型为回归模型，且房价作为目标变量数值较大， 需对其进行对数处理以保证后续构建模型的有效性。

        2.参数调优结果

        通过设置合理的网格搜索区间，搜索出基于训练集的最佳模型参数，可以构建相对初始模型更佳有效的模型。

        3.交叉检验结果

         初始模型：

        

        参数调优后模型：

        

        可以看出，模型进行网格参数调优后，在以均方根误差（RMSE）为评价指标的情况下，最优参数模型比初始模型表现更好，实现了房屋价格预测模型的优化。

        4.模型特征重要性可视化

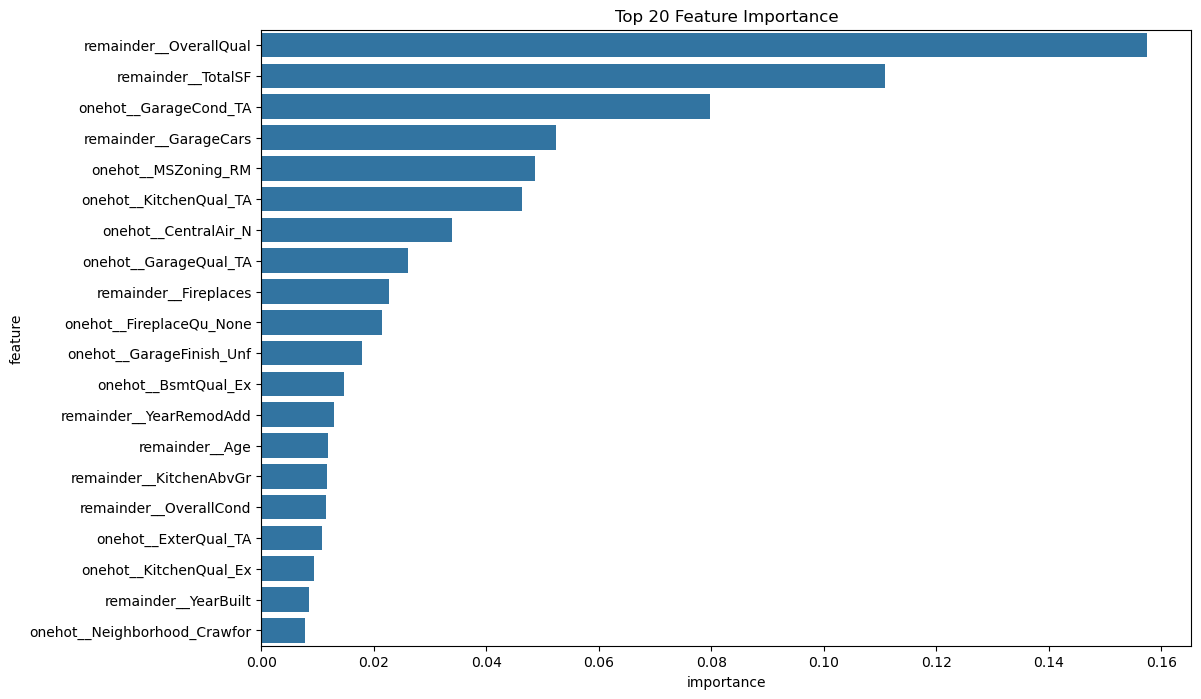
        可以看出，在最终模型里，“remainder__OverallQual”（房屋整体材料和装修质量）是预测房价的最关键因素；“remainder__TotalSF”（房屋总面积）的重要性紧随其后，可以解释为面积越大通常价格越高；“remainder__GarageCars”（车库容纳车辆数）的重要性也较高，因为其间接反映车库大小。

（五）总结 

        本实验基于kaggle上的房屋价格数据集，通过数据预处理与参数调优，成功通过XGBoost回归构建了一个能够准确预测房屋价格的模型。其中，房屋质量（OverallQual）、面积（TotalSF）和车库属性（GarageCond_TA、GarageCars）是房价预测模型的核心特征。

        可优化方向：基于特征重要性图，对于低重要性特征可尝试剔除以简化模型，但需验证对性能的影响；也可以尝试其他不同的回归模型（如线性回归模型，神经网络模型等），综合比较出最优模型进行实际应用。