获取更多资讯，赶快关注公众号《智能制造与智能调度》吧！

作者简介：王东海，上海交通大学博士在读，专注于智能制造领域的排产调度优化，主要研究基于强化学习、机器学习、运筹优化的前沿方法，探索复杂生产环境下的动态排产与调度策略，旨在实现工业实际场景中的智能化排程与调度优化，推动生产系统多目标的协同优化。

1. 摘要

柔性机器人单元在柔性化和定制化制造中起着至关重要的作用。有效的调度策略可以显著减少最大完工时间，提高生产效率。作者引入了一种创新的基于深度强化学习（DRL）的端到端实时调度方法，以最小化柔性机器人单元的最大完工时间，在异构析取图模型中通过特定析取弧考虑运输因素。在方法上，DRL利用图神经网络（GNN）进行模型特征提取，并采用近端策略优化（PPO）训练调度智能体，以更好地利用运输机器人的能力，减少系统阻塞和死锁。

2. 背景

机器人制造单元由多台机器和一个机器人组成。该机器人可以在机器之间自动运输工件，从而提高生产率。

按照机器柔性和所能加工的零件类型，可以将制造单元的发展历经3个阶段，如图1所示：

• 单零件类型：传统模式下实现大规模生产；
• 多零件类型：不改变原有生产流程，采用并行机器和多容量运输机器人；
• 多零件类型+可选机器：每个产品可具有不同的生产流程，每道工序存在多个可选机器。

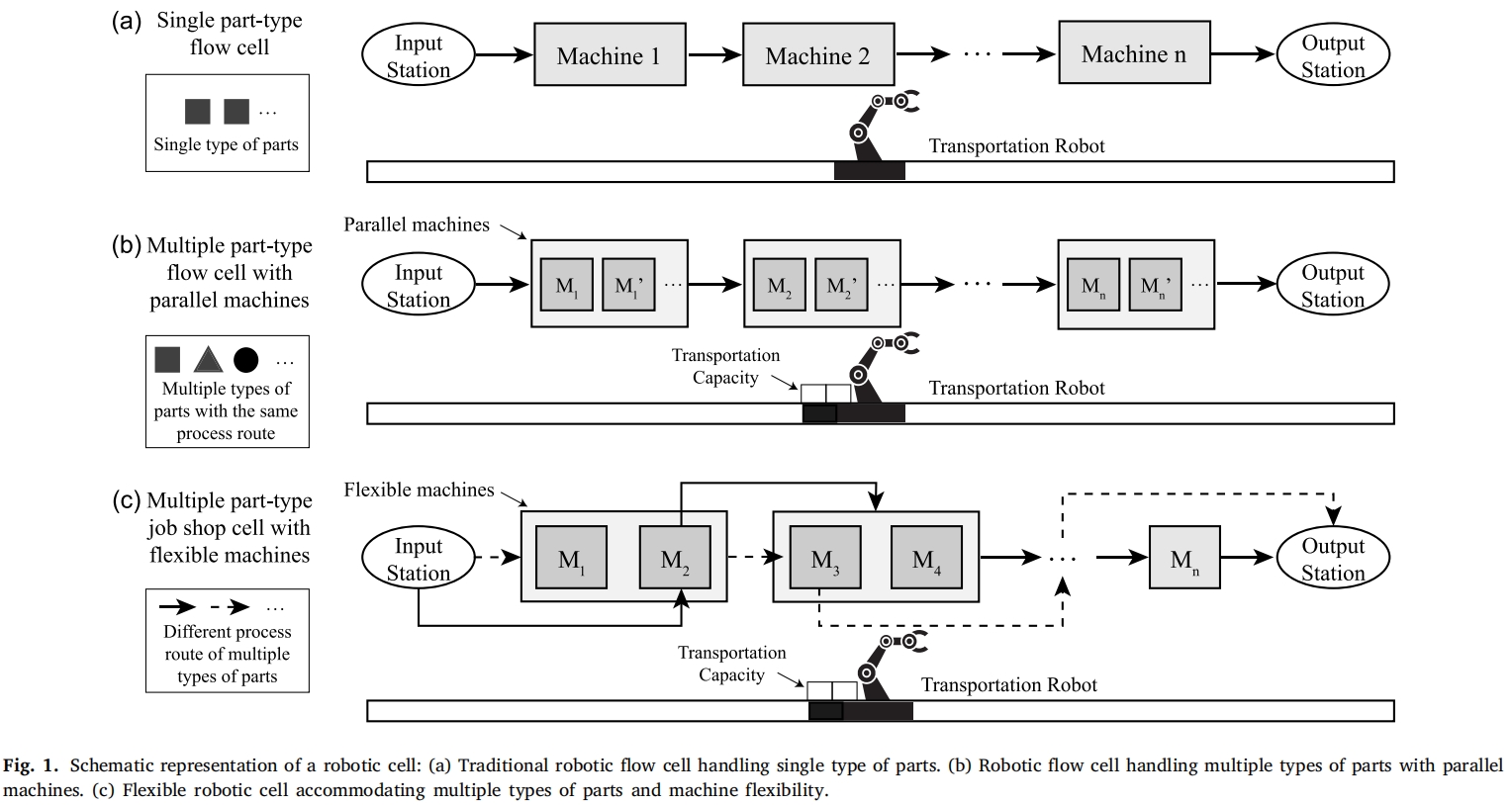
柔性机器人单元调度包括机器人动作排序和工序机器选择。运输约束、缺乏中间缓冲区和死锁避免等因素给该问题增加了更多挑战。

为此，作者提出了一种基于端到端DRL的实时调度方法，用于具有多容量运输机器人的柔性机器人单元。优化目标是最大完工时间。该方法的核心是基于一种新颖的异构析取图模型，用于表达工序和机器节点之间的成对有向析取弧从而表示运输动作。此外，采用图神经网络从这个复杂的状态空间中提取特征，以确保对所有工序及其与机器的相互关系进行全面分析。通过采用动作掩码，DRL能够确保调度计划的可行性并防止死锁。

该方法能够自适应不同规模的调度问题，无需重新训练，特别适合复杂调度问题实时调度策略的全局优化。

3. 问题表述与模型建立

3.1问题表述

柔性机器人单元的调度定义如下，符号定义如下。

一个柔性机器人单元由输入站、输出站、机器和一个运输机器人组成。一组包含n个工件的集合J={J1,...,Jn}J=\{J_{1},..., J_{n}\}J={J1​,...,Jn​}将在具有$m$台机器的机器集合$M$上进行加工。每个作业$J_i\in J$将从输入站进入单元，然后经过一系列固定的工序Oi={Oi1,...,Oini}O_{i}=\{O_{i1},..., O_{i n_{i}}\}Oi​={Oi1​,...,Oini​​}，最终从输出站离开单元。每个操作$O_{ij}$可以由一组可选机器$M_{ij}$执行，相应的加工时间为$p_{ijk}$，其中$M_k\in M_{ij}$。

在机器人单元内，运输机器人将作业从输入站通过加工阶段移动到输出站。机器人通过执行以下两个过程以在两个工作站之间移动工件：

1. 运输机器人移动到一台机器或输入站，并卸载其工件。
2. 运输机器人将作业移动到下一个加工机器或输出站，并将作业装载到工作站上。

每个运输过程包括机器人在机器之间的移动时间$t_{k{k}^{\prime }}^{trans}$以及将工件装载（$t_{load}$）或卸载（$t_{unload}$）到机器人的时间，这些时间在单元内是固定的。

优化目标是最小化最大完工时间，即所有作业完成加工并运输到输出站的时间。

对问题作出以下假设：

• 单元中无缓冲区，即当前工件从机器上移除之前，机器不能接受新的工件；
• 初始，所有工件和运输机器人位于输入站，所有机器可用；
• 每个工序可以由一组可选机器以固定的加工时间执行；
• 每台机器一次只能处理一个工件，并且一旦开始，加工过程不能暂停或中断；
• 每个工件一次只能由一台机器处理；
• 不同工作站之间的运输时间以及机器人的装载和卸载时间是预先确定且固定的；
• 运输机器人的容量（>1）有限；
• 输出站的容量无限，作业只有在完成所有操作后才能放置在输出站。

3.2柔性机器人单元的析取图模型

析取图模型$\mathcal{H}=(\mathcal{O},\mathcal{M},\mathcal{C},\mathcal{E})$定义如图2所示。

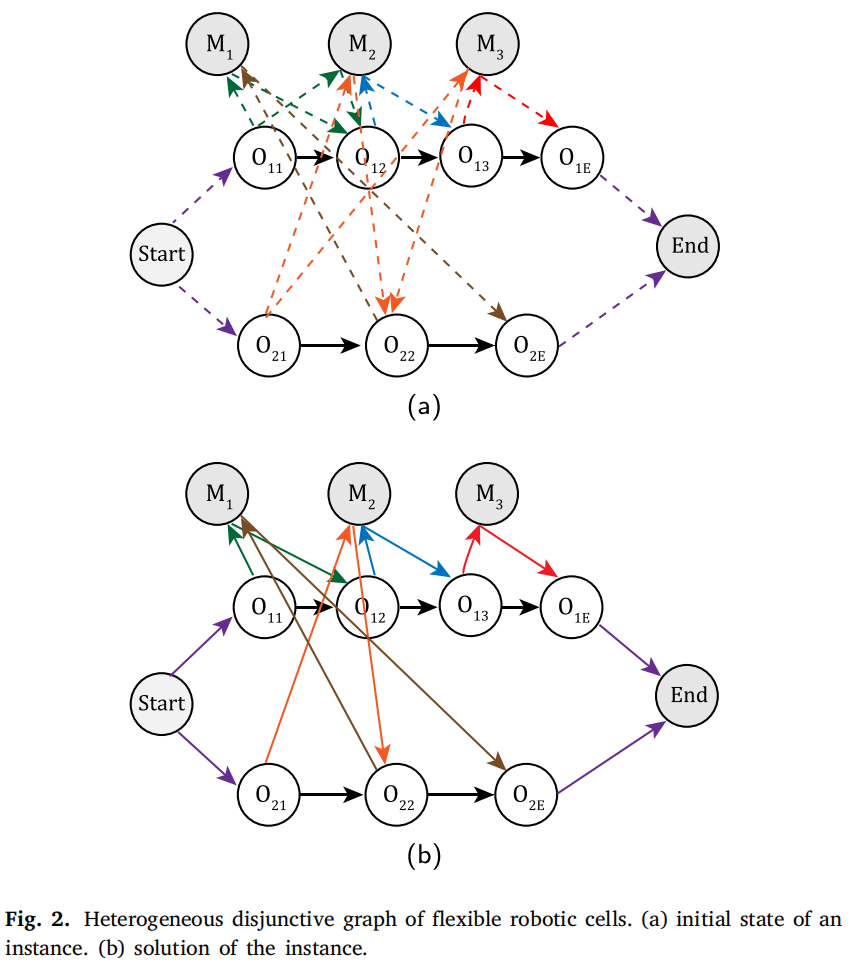
各部分的含义如下：

• O={O11,…,O1n1,O1E,O21,…,O2E,…,On1,…,OnE}\mathcal{O}=\{O_{11}, …, O_{1n_1}, O_{1E}, O_{21}, …, O_{2E}, …, O_{n1}, …, O_{nE}\}O={O11​,…,O1n1​​,O1E​,O21​,…,O2E​,…,On1​,…,OnE​}是工序节点集合，其中$O_{ij}$表示工件$J_i$的第$j$个工序。对于每个工件$J_i$，在最后工序$O_{i{n}_1}$之后引入一个额外的虚拟完成工序节点$O_{iE}$，以完全捕获运输过程。工序$O_{iE}$只能由输出站处理。
• M={M1,...,Mm}\mathcal{M}=\{M_{1},..., M_{m}\}M={M1​,...,Mm​}是机器节点集合。每个节点$M_i$对应于单元中的一台机器。所提出的模型将开始和结束节点视为机器节点，以将装载和卸载站纳入析取图模型。
• $\mathcal{C}$是连接弧集，其中有向弧连接同一工件的不同工序以表示工序加工顺序。与一般析取图模型不同，连接到开始和结束节点的弧不包括在连接弧集中。
• E={Ein∪Eout}\mathcal{E}=\{\mathcal{E}_{in } \cup \mathcal{E}_{out }\}E={Ein​∪Eout​}是成对析取弧集，表示机器与工序之间的关系。每对析取弧由{Oij→Mk}∈Ein\{O_{i j} \to M_{k}\} \in \mathcal{E}_{in}{Oij​→Mk​}∈Ein​和{Mk→Oi,j+1}∈Eout\{M_{k} \to O_{i, j+1}\} \in \mathcal{E}_{out }{Mk​→Oi,j+1​}∈Eout​组成。{Oij→Mk}\{O_{i j} \to M_{k}\}{Oij​→Mk​}表示$O_{ij}$可以由$M_k$处理，表示将$J_i$运输到$M_k$。而{Mk→Oi,j+1}\{M_{k} \to O_{i, j+1}\}{Mk​→Oi,j+1​}表示从$M_k$卸载$J_i$并将其存储在机器人上，为$O_{i,j+1}$做准备。对于涉及$O_{iE}$的弧，$M_k\to O_{iE}$表示从$M$卸载$J_i$并将其存储在机器人上，{OiE→End}\{O_{iE} \to End \}{OiE​→End}表示将$J_i$运输到输出站。

基于所提出的模型，运输调度过程的特点是选择析取弧。需要注意的是，在选择弧{Oij→Mk}\{O_{i j} \to M_{k}\}{Oij​→Mk​}之后，需要删除连接工序到不同机器的其他对弧。换句话说，析取弧集$\mathcal{E}$随时间变化。

以上图中工件$J_2$的处理为例。初始，{Start→O21}\{Start \to O_{21}\}{Start→O21​}弧表示从输入站卸载$J_2$。随后，选择{O21→M2}\{O_{21} \to M_{2}\}{O21​→M2​}弧表示机器人运输并将$J_2$卸载到$M_2$上以启动加工$O_{21}$。同时，弧对{O21→M3}\{O_{21} \to M_{3}\}{O21​→M3​}和{M3→O22}\{M_{3} \to O_{22}\}{M3​→O22​}被删除。该过程不断迭代，然后{M1→O2E}\{M_{1} \to O_{2E}\}{M1​→O2E​}弧表示将完成的作业从机器上取回并放置在机器人上。最后，{O2E→End}\{O_{2E} \to End \}{O2E​→End}表示机器人将作业运输到输出站并卸载$J_2$，标志着$J_2$的加工完成。

因此，在柔性机器人单元调度问题中，在每个离散时间步$t$，单元的状态可表达为${\mathcal{H}}_t=(\mathcal{O},\mathcal{M},\mathcal{C},{\mathcal{E}}_t)$。然后在这个模型中选择合法的析取弧，运输机器人执行相应的动作。状态空间然后转换为${\mathcal{H}}_{t+1}$。值得注意的是，运输机器人在一个时间步可以不选择弧，即原地等待下一个时间步，这更符合实际工程实践。

4. 基于DRL的调度方法

为了获得机器人单元的实时优化调度策略，本文采用了深度强化学习（DRL）方法，并基于给定机器人单元的离散事件仿真进行模拟。从制造系统的初始状态开始，在每个时间步$t$和状态$s_t$，模拟环境根据动作$a_t$生成下一个时间步$t+1$和相应的状态$s_{t+1}$。这个过程一直持续到系统完成所有处理任务。强化学习通过与制造系统模拟模型的交互促进了调度智能体的训练和测试。算法的整体机制如图3所示。

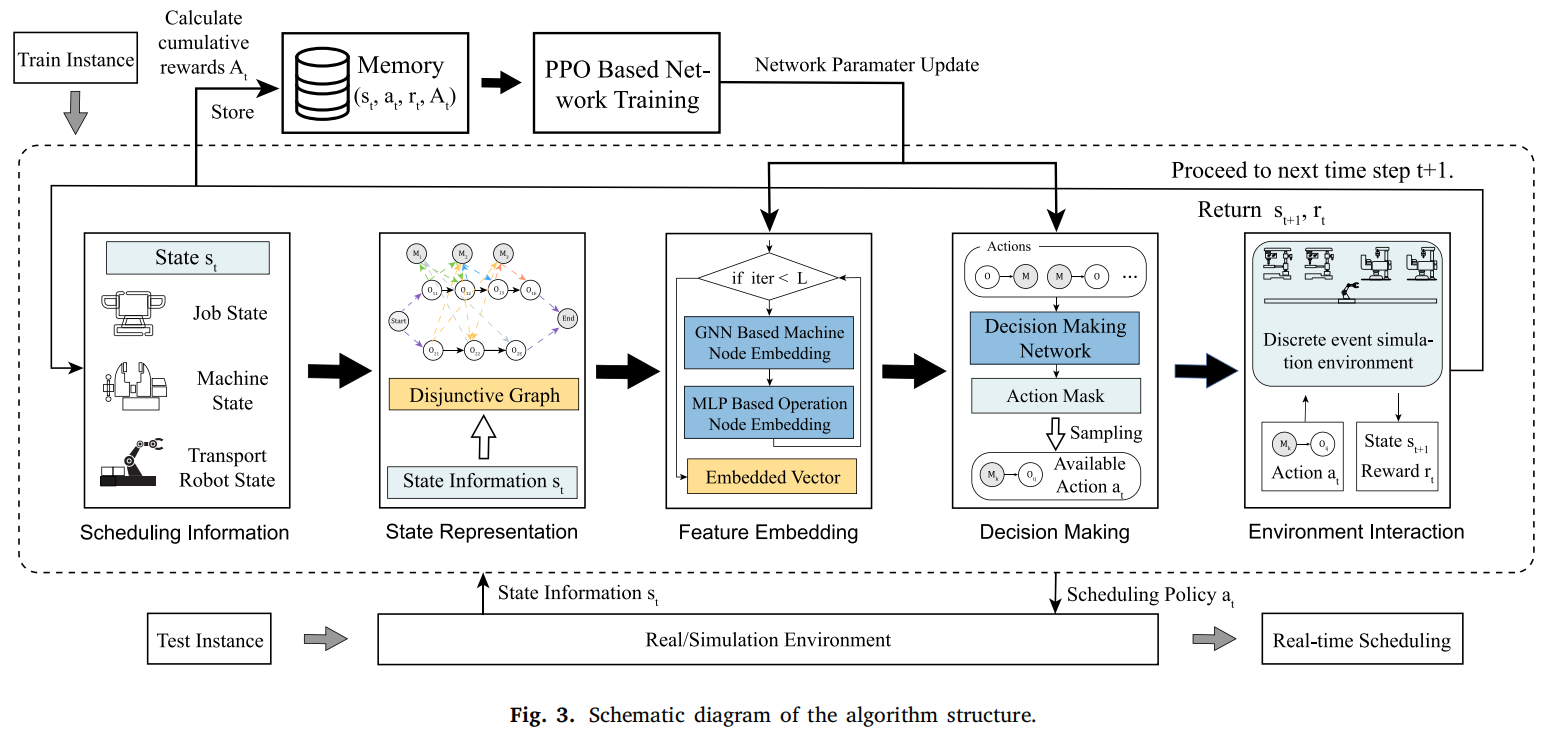
4.1调度环境的建立

4.1.1状态空间

在时间$t$，状态空间$s_t$包含有关工件、机器和运输机器人的全面信息，主要由异构模型${\mathcal{H}}_t$进行表征。该模型封装了工序节点、机器节点和析取弧的固有特征，作为强化学习智能体的关键输入。

具体而言，对于工件$J_i$的每个工序节点$O_{ij}$，其嵌入特征向量${\mu }_{ij}\in {\mathbb{R}}^8$包括以下元素：

• 表示$O_{ij}$是否已进行运输的二进制指示符，即弧{M→Oij}\{M \to O_{i j}\}{M→Oij​}是否已执行。
• $O_{ij}$的状态，分为未处理、处理中或已完成。
• 可以处理$O_{ij}$的机器数量。
• $O_{ij}$的加工时间。
• $O_{ij}$运输的起始时间，表示弧{M→Oij}\{M \to O_{i j}\}{M→Oij​}执行的时刻。
• $O_{ij}$加工的起始时间，表示弧{Oij→M}\{O_{i j} \to M\}{Oij​→M}执行的时刻。
• $J_i$中尚未完成的工序数量。
• $J_i$的完成率。

需要强调的是，对于时刻$t$还未开始加工的工序而言，由于未选定机器，其加工时间并不确定，因而使用所有可选机器的平均加工时间代替，即${\bar{p}}_{ij}={\sum }_{M_k\in {\mathcal{M}}_{ij}}{p}_{ijk}/|{\mathcal{M}}_{ij}|$。

对于机器节点$M_k$，其嵌入特征$v_k\in {\mathbb{R}}^5$包括：

• $M_k$的状态，分为空闲、处理中或已完成。
• $M_k$的剩余加工时间。
• $M_k$邻域内的工序数量。
• $M_k$的利用率，定义为机器$M_k$有效加工工件的时间与总经过时间的比率。
• 运输机器人当前是否位于$M_k$的二进制。

特别地，由于将$Start$和$End$视为机器节点，它们也需要分配特征。模型规定$Start$和$End$节点的状态始终为空闲，其剩余加工时间为$0$，利用率为$1$。

对于析取弧集，即成对的入弧{Oij→Mk}\{O_{i j} \to M_{k}\}{Oij​→Mk​}和出弧{Mk→Oi,j+1}\{M_{k} \to O_{i, j+1}\}{Mk​→Oi,j+1​}，其嵌入特征${\lambda }_{ijk}^{in}\in {\mathbb{R}}^3$和${\lambda }_{ijk}^{out}\in {\mathbb{R}}^3$如下：

• 弧运输动作后的工序加工时间，即对于$O_{ij}\to M_k$为$p_{ijk}$，对于$M_k\to O_{i,j+1}$为${\bar{p}}_{i,j+1}$。
• 与弧相关的运输动作所消耗的时间。
• 运输机器人上的作业数量。

4.1.2动作

在时间$t$，动作空间$A_t$由析取弧集${\mathcal{E}}_t$和一个额外的“等待”动作组成。当选择“等待”动作时，运输机器人保持空闲，直到下一个离散事件，具体来说，这个事件是指当任何机器完成其当前工序时。通过引入“等待”动作来提升算法探索能力。

在每个时间步，应用动作掩码从动作空间$A_t$中过滤掉不可行的动作，例如选择当前被其他作业占用的机器，确保即使可行动作的数量随时间波动，动作空间维度也保持一致。

此外，为了防止死锁，算法在为待处理的加工和运输任务选择动作时评估机器可用性和机器人容量。在运输机器人满载或所有必要机器被占用的情况下实施动作限制，从而防止选择可能导致死锁的动作。

4.1.3奖励

在状态$s_t$采取动作$a_t$的奖励定义如下：

$$R\left(s_t,a_t,s_{t+1}\right)=p_{aj}-\sum _{m\in \mathcal{M}}empt{y}_m\left(s_t,s_{t+1}\right)\text{\hspace{1em}(1)}$$

这里，$p_{aj}$表示与动作相关的工序的加工时间。如果当前动作未启动任何工序的加工，则$p_{aj}$设置为$0$。${\sum }_{m\in \mathcal{M}}empt{y}_m(s_t,s_{t+1})$表示直到下一个时间步所有机器的空闲时间总和。

在调度问题中，累积奖励反映了工序的总加工时间减去机器的总空闲时间。因此可以通过最大化累积奖励来减少机器空闲时间和生产最大完工时间。

4.2 DRL框架

本文采用基于的强化学习算法框架，并通过结合有向析取弧对的特征嵌入来增强其在柔性机器人单元中的性能，采用如下网络结构。

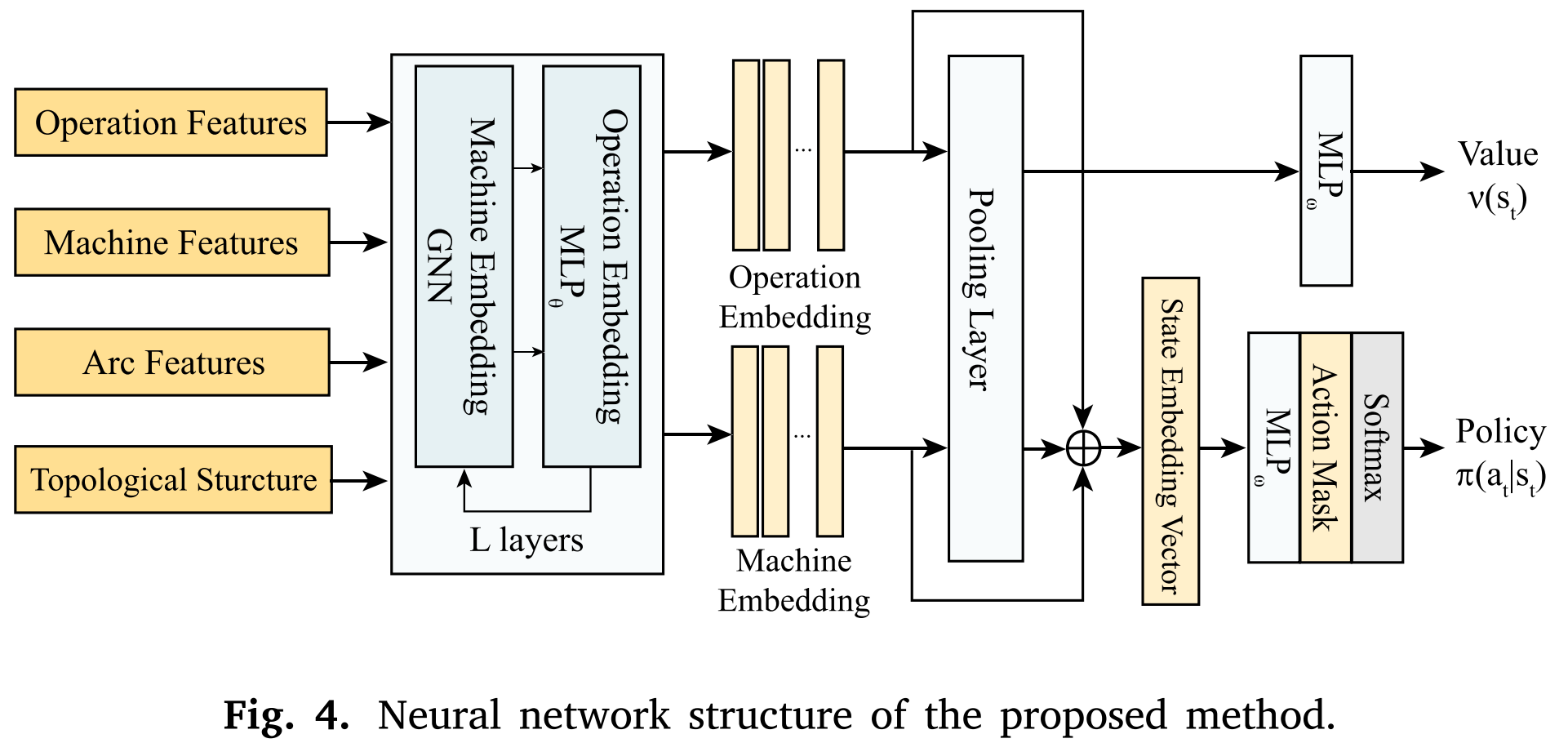
4.2.1特征嵌入

对于所提出的析取图模型，分别对三种类型的弧（连接弧、入度析取弧和出度析取弧）及其相应的节点连接进行特征嵌入。对于状态空间${\mathcal{H}}_t$，首先基于邻域节点和析取弧状态获得机器节点的$d$维嵌入$v_k^{\prime }$。然后进一步更新工序节点的嵌入状态以获得$d$维嵌入向量${\mu }_{ij}^{\prime }$。

详细细节如下：

机器节点嵌入

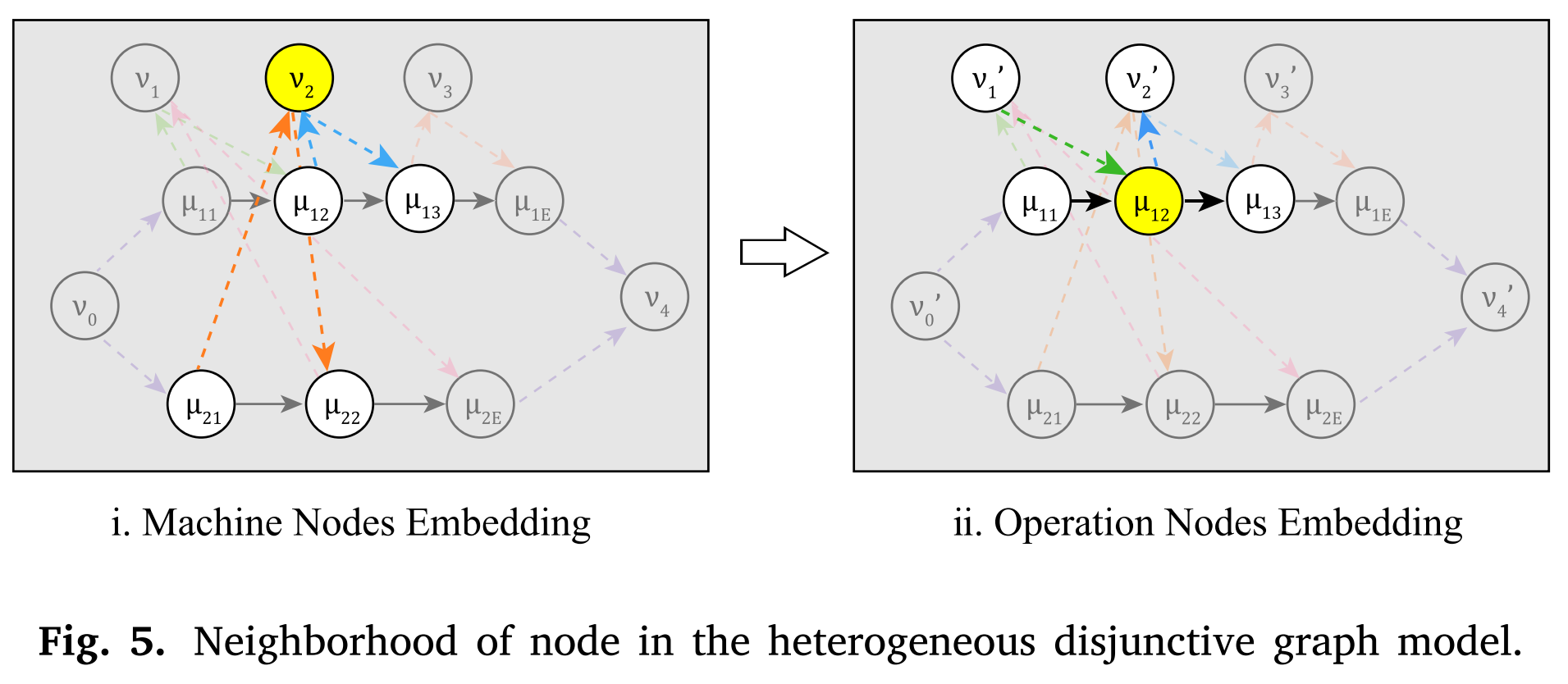
对于每个机器节点，如图5所示，其相邻节点仅为通过成对析取弧连接的g工序节点。为了将析取弧特征纳入节点特征，算法采用图注意力网络（Graph Attention Networks）。

对于机器$M_k$及其邻域${\mathcal{N}}_t(M_k)={\mathcal{N}}_t^{in}(M_k)\cup {\mathcal{N}}_t^{out}(M_k)$，将析取弧特征集成到节点特征中。具体而言，如果$O_{ij}\in {\mathcal{N}}_t^{in}(M_k)$，那么定义${\mu }_{ijk}^{in}=[{\mu }_{ij}\Vert {\lambda }_{ijk}^{in}]$，如果$O_{ij}\in {\mathcal{N}}_t^{out}(M_k)$，那么定义${\mu }_{ijk}^{out}=[{\mu }_{ij}\Vert {\lambda }_{ijk}^{out}]$，其中${\mu }_{ijk}^{in},{\mu }_{ijk}^{out}\in {\mathbb{R}}^{11}$。注意力系数$e_{ijk}^{in},e_{ijk}^{out}$通过线性变换$W^M$、$W^{in}$、$W^{out}$计算如下：

$$e_{ijk}^{in}=LeakyReLU\left(a^{\top }\left[W^M{v}_k\Vert W^{in}{\mu }_{ijk}^{in}\right]\right)\text{\hspace{1em}(2)}$$

$$e_{ijk}^{out}=LeakyReLU\left(a^{\top }\left[W^M{v}_k\Vert W^{out}{\mu }_{ijk}^{out}\right]\right)\text{\hspace{1em}(3)}$$

这里，$a^{\top }\in {\mathbb{R}}^{2d}$。机器节点与其自身的注意力系数$e_{kk}$定义为：

$$e_{kk}=LeakyReLU\left(a^{\top }\left[W^M{v}_k\Vert W^M{v}_k\right]\right)\text{\hspace{1em}(4)}$$

然后应用Softmax函数对注意力系数进行归一化，得到${\alpha }_{ijk}^{in}$、${\alpha }_{ijk}^{out}$和${\alpha }_{kk}$。最后，机器节点嵌入$v_k^{\prime }$计算如下：

$$v_k^{\prime }=\sigma \left({\alpha }_{kk}{W}^M{v}_k+\sum _{O_{lj}\in {\mathcal{N}}_t^{in}\left(M_k\right)}{\alpha }_{ijk}^{in}{W}^{in}{\mu }_{ijk}^{in}+\sum _{O_{ij}\in {\mathcal{N}}_f^{out}\left(M_k\right)}{\alpha }_{ijk}^{out}{W}^{out}{\mu }_{ijk}^{out}\right)\text{\hspace{1em}(5)}$$

需要注意的是，$Start$和$End$节点也被视为机器节点，并对其应用特征嵌入。

工序节点嵌入

对于操作节点$O_{ij}$，如图5(ii)所示，连接节点包括前置工序$o_{i,j-1}$、后置工序$o_{i,j+1}$和机器节点${\mathcal{N}}_t(O_{ij})={\mathcal{N}}_t^{in}(O_{ij})\cup {\mathcal{N}}_t^{out}(O_{ij})$。算法采用多层感知器$(ML{P}_{{\theta }_1},...,ML{P}_{{\theta }_5})$来识别和嵌入相应的特征。此外，统一使用神经网络$ML{P}_{{\theta }_0}$来合并这些特征。具体而言，对于具有多个机器选择的工序节点，使用特征总和来替换每个连接机器节点的相同类型的特征，这通过设置${\bar{v}}_{ij}^{i{n}^{\prime }}={\sum }_{k\in {\mathcal{N}}_t^{in}(O_{ij})}{v}_k^{\prime }$，${\bar{v}}_{ij}^{out}={\sum }_{k\in {\mathcal{N}}_t^{ou{t}^{\prime }}(O_{ij})}{v}_k^{\prime }$来实现。工序节点嵌入${\mu }_{ij}^{\prime }$然后由下式给出：

$${\mu }_{ij}^{\prime }=ML{P}_{{\theta }_0}\left(ELU\left[ML{P}_{{\theta }_1}\left({\mu }_{i,j-1}\right)\Vert ML{P}_{{\theta }_2}\left({\mu }_{i,j+1}\right)\Vert ML{P}_{{\theta }_3}\left({\overline{v}}_{ij}^{i{n}^{\prime }}\right)\Vert ML{P}_{{\theta }_4}\left({\overline{v}}_{ij}^{ou{t}^{\prime }}\right)\Vert ML{P}_{{\theta }_5}\left({\mu }_{ij}\right)\right]\right)\text{\hspace{1em}(6)}$$

嵌入迭代

对得到机器和工序节点嵌入$v_k^{\prime }$和${\mu }_{ij}^{\prime }$进行$L$次迭代嵌入从而获得最终嵌入，表示为$v_k^{(L)}$和${\mu }_{ij}^{(L)}$。在整个迭代过程中，析取弧特征${\lambda }_{ijk}^{in}$和${\lambda }_{ijk}^{out}$保持不变，而机器和工序节点特征不断更新。

4.2.2策略生成

在完成给定状态$s_t$的特征嵌入后，下一步是生成动作策略$\pi (a_t|s_t)$，其中$a_t\in A_t$。算法首先通过对嵌入特征进行平均池化来启动此过程，得到$h_t\in {\mathbb{R}}^{2d}$：

$$h_t=\left[\frac{1}{|\mathcal{O}|}\sum _{O_{ij}\in \mathcal{O}}{\mu }_{ij}^{(L)}\Vert \frac{1}{|\mathcal{M}|}\sum _{M_k\in \mathcal{M}}{v}_k^{(L)}\right]\text{\hspace{1em}(7)}$$

随后，将获得的嵌入特征与池化特征连接，并输入到$ML{P}_{\omega }$中，得到状态$s_t$下每个动作的得分$P(a_t,s_t)$：

$$P\left(a_t,s_t\right)=ML{P}_{\omega }\left[{\mu }_{ij}^{(L)}\Vert v_k^{(L)}\Vert h_t\right]\text{\hspace{1em}(8)}$$

获得得分后，该方法对动作空间应用动作掩码。此过程将不可行动作的得分设置为$-\infty$，以在策略生成期间有效避免采取不可行动作。

此外，对策略得分应用Softmax函数进行归一化，得到调度策略：

$$\pi \left(a_t|s_t\right)=\frac{\text{exp}\left(P\left(a_t,s_t\right)\right)}{{\sum }_{a_t^{\prime }\in A_t}\text{exp}\left(P\left(a_t^{\prime },s_t\right)\right)}\forall a_t\in A_t\text{\hspace{1em}(9)}$$

对于不可行动作，由于得分是$-\infty$，归一化后的概率为$0$。在训练过程中，根据可行动作的概率分布进行随机动作选择，以扩展算法的探索空间。

4.2.3训练算法

本文采用由Schulman提出的近端策略优化算法（PPO）进行训练。该算法使用两个神经网络，即演员（Actor）和评论家（Critic）。演员的作用是根据环境的当前状态选择动作，而评论家评估状态-动作对的价值。演员和评论家网络进行联合训练，评论家向演员网络提供关于所选动作质量的反馈。

在训练期间，策略生成网络（表示为$ML{P}_{\omega }$）充当演员，$ML{P}_{\varphi }$配置为评论家，负责评估策略的价值。评论家网络$ML{P}_{\varphi }$的架构与演员网络$ML{P}_{\omega }$相似，区别在于其输入是池化特征$h_t$。算法1概述了DRL的训练过程。

5.数值实验

5.1实验设置

机器人运输能力默认为2，其他详细参数配置可查看原文。

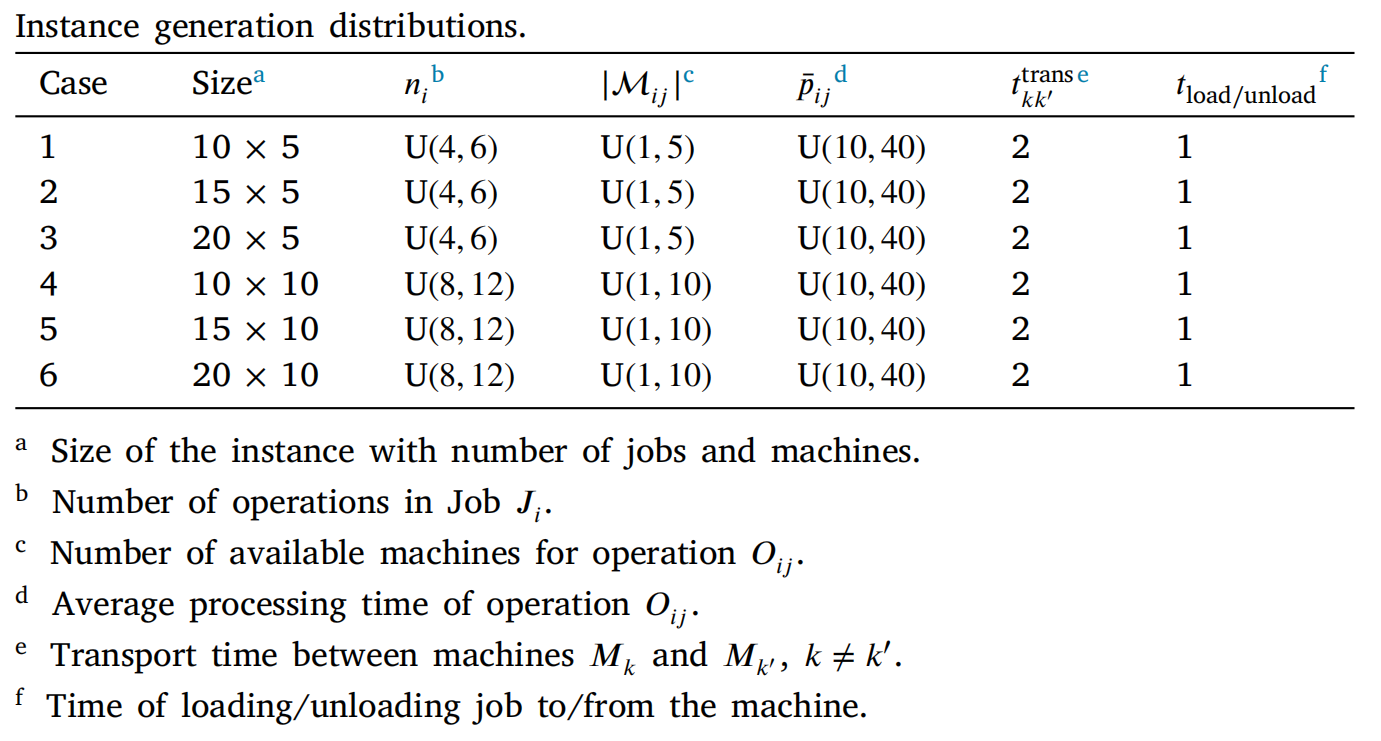
训练算法与四种规则方法进行了比较：先进先出（FIFO）、最短加工时间（SPT）、最短总加工时间（STPT）和剩余工序数最少（LOR）。

该方法评估的指标包括完工时间$C_{max}$和相对gap $ϵ$。相对差距$ϵ$定义为公式(10)，其中$C_{\text{max}}^{BS}$是规则方法和DRL方法求得的最优完工时间。

$$ϵ=\left(\frac{C_{\text{max}}-C_{\text{max}}^{BS}}{C_{\text{max}}^{BS}}\right)\times 100\%\text{\hspace{1em}(10)}$$

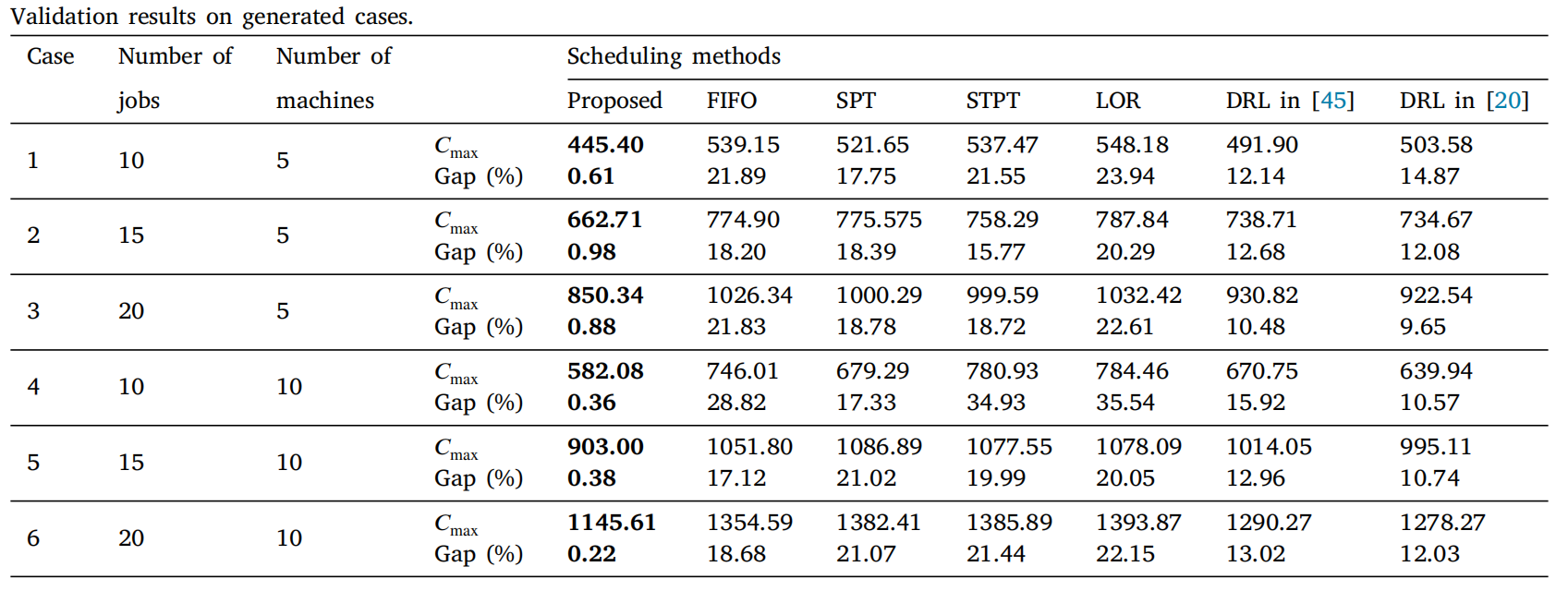
5.2随机案例实验

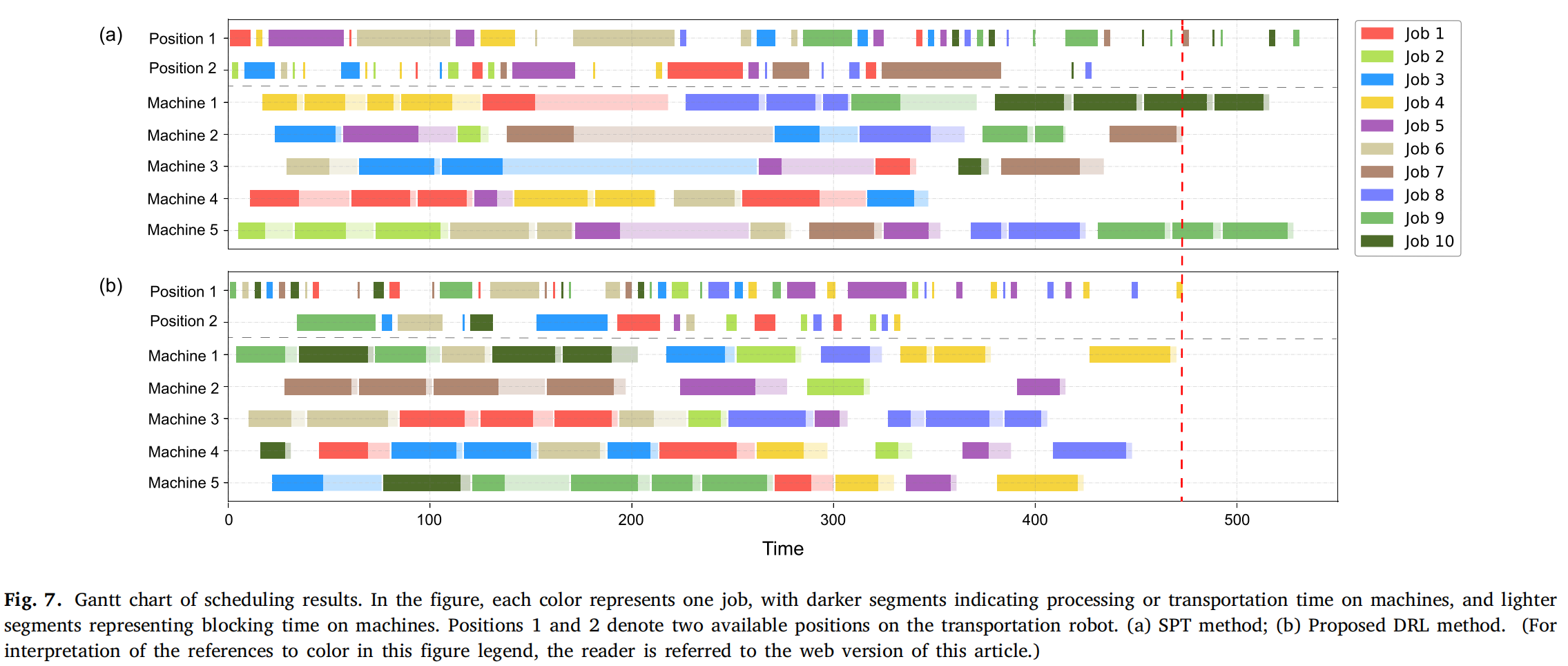
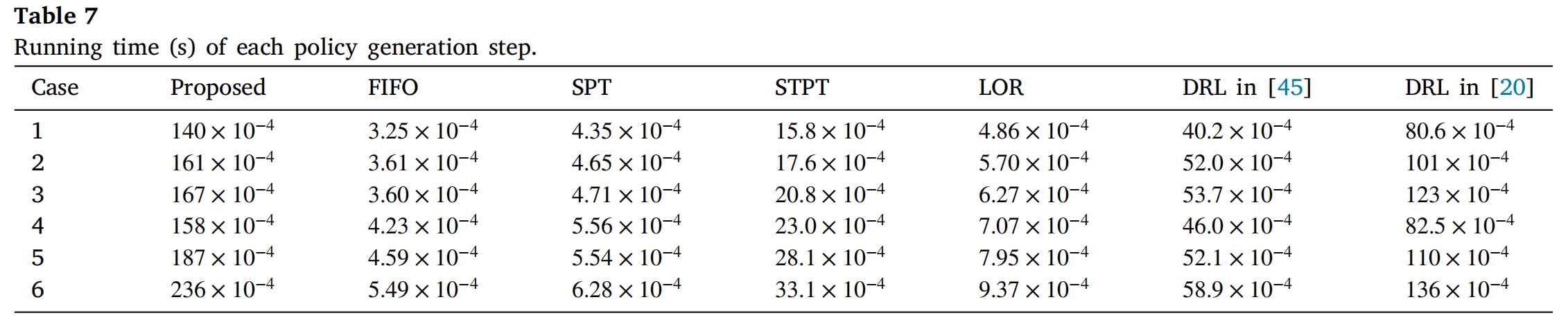
5.3消融实验

通过消融研究以检验：

• 基于GNN的特征嵌入 vs 简单池化策略（模型1）
• 状态空间构建 vs 文献【45】中的状态空间设计（模型2）
• 奖励函数设计 vs 文献【20】中的奖励函数）模型3

可以看出，与作者提出的模型相比，模型1的性能受到影响最大，完工时间增加了8%-18%。这强调了GNN在捕捉柔性机器人单元中机器、工件和工序之间复杂关系方面的重要性。模型2和3的完工时间分别增加了5%-10%和4%-8%。因此，状态空间构建和奖励函数设计对于描述系统动态和决策制定也必不可少。

5.4 标准案例实验

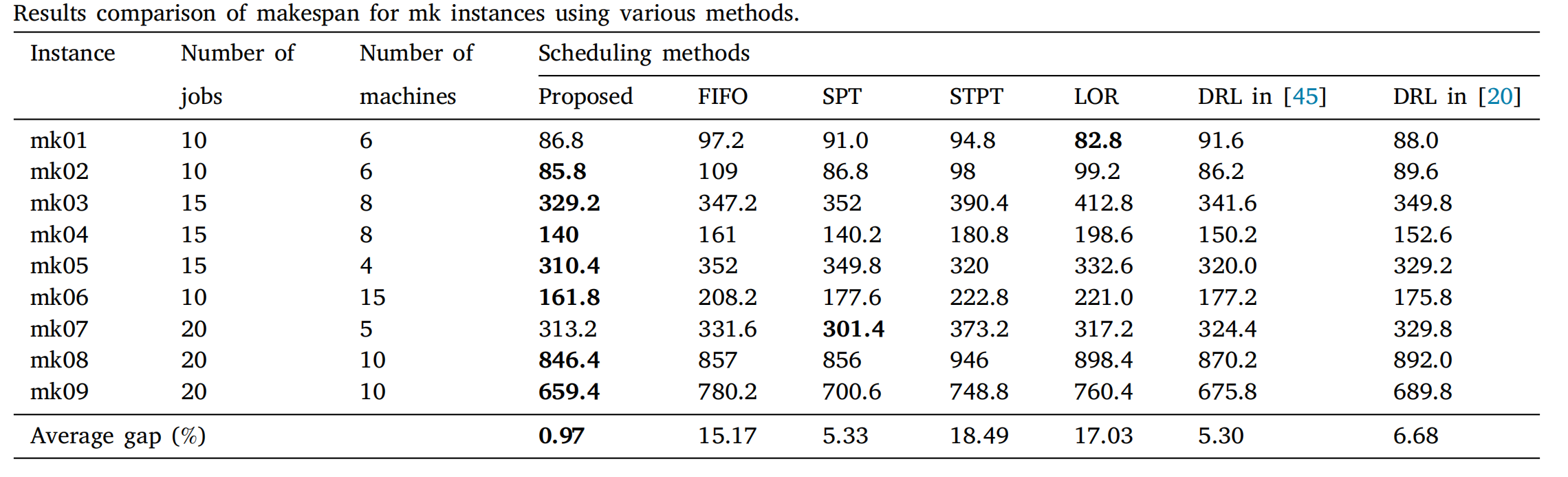
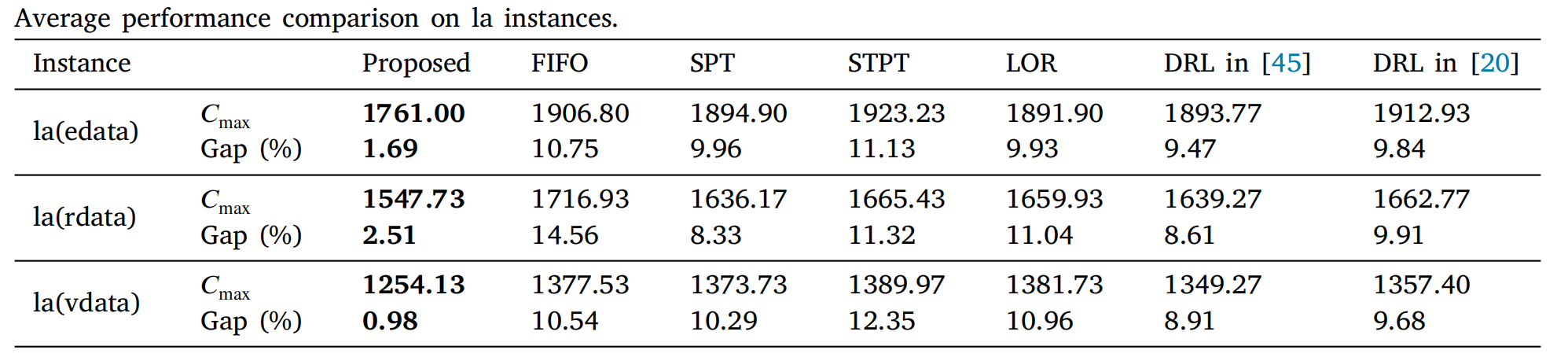
直接将随机案例训练出的模型应用于标准案例集，进一步验证泛化能力。

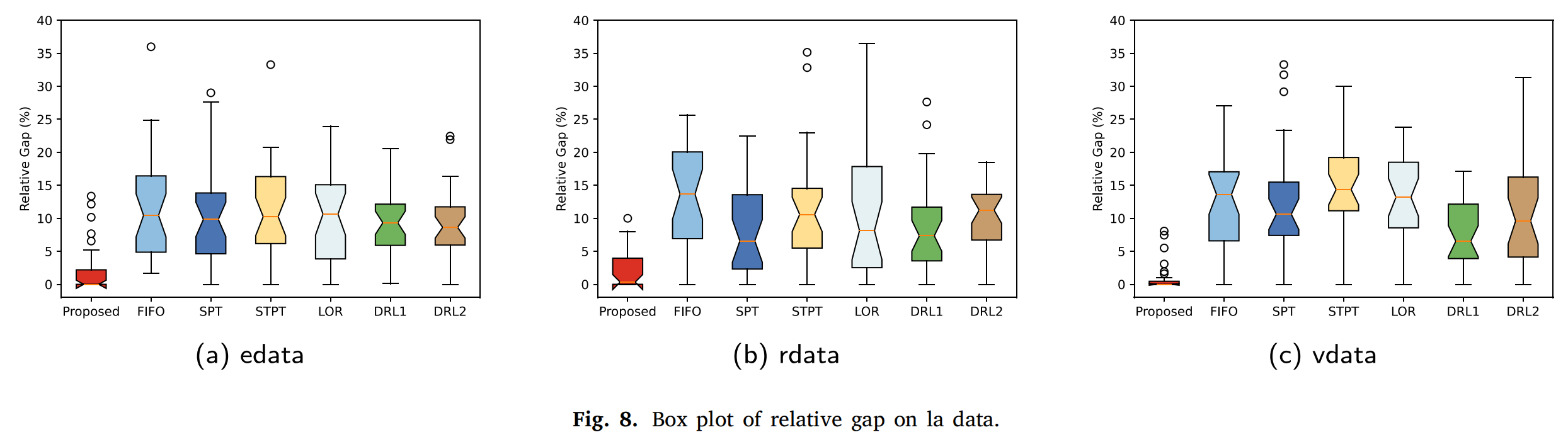
5.5 运输能力的讨论

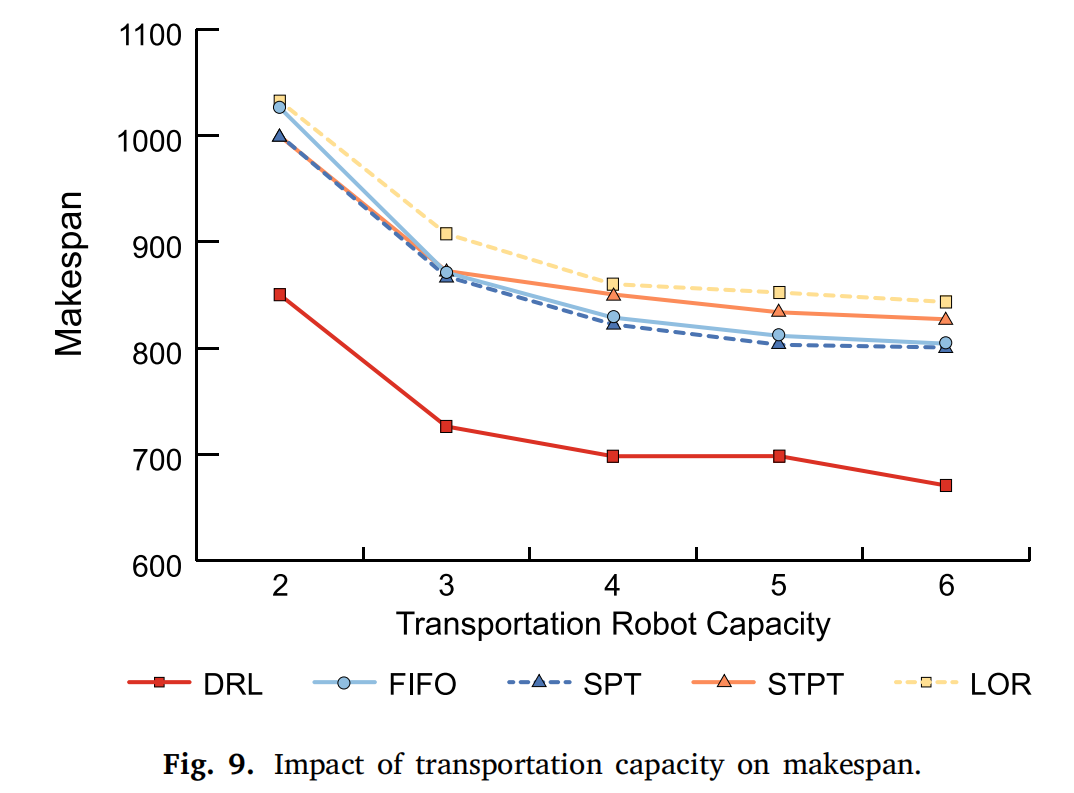
随着运输能力的增加，系统处理作业的能力变得更加灵活，导致处理时间显著减少。

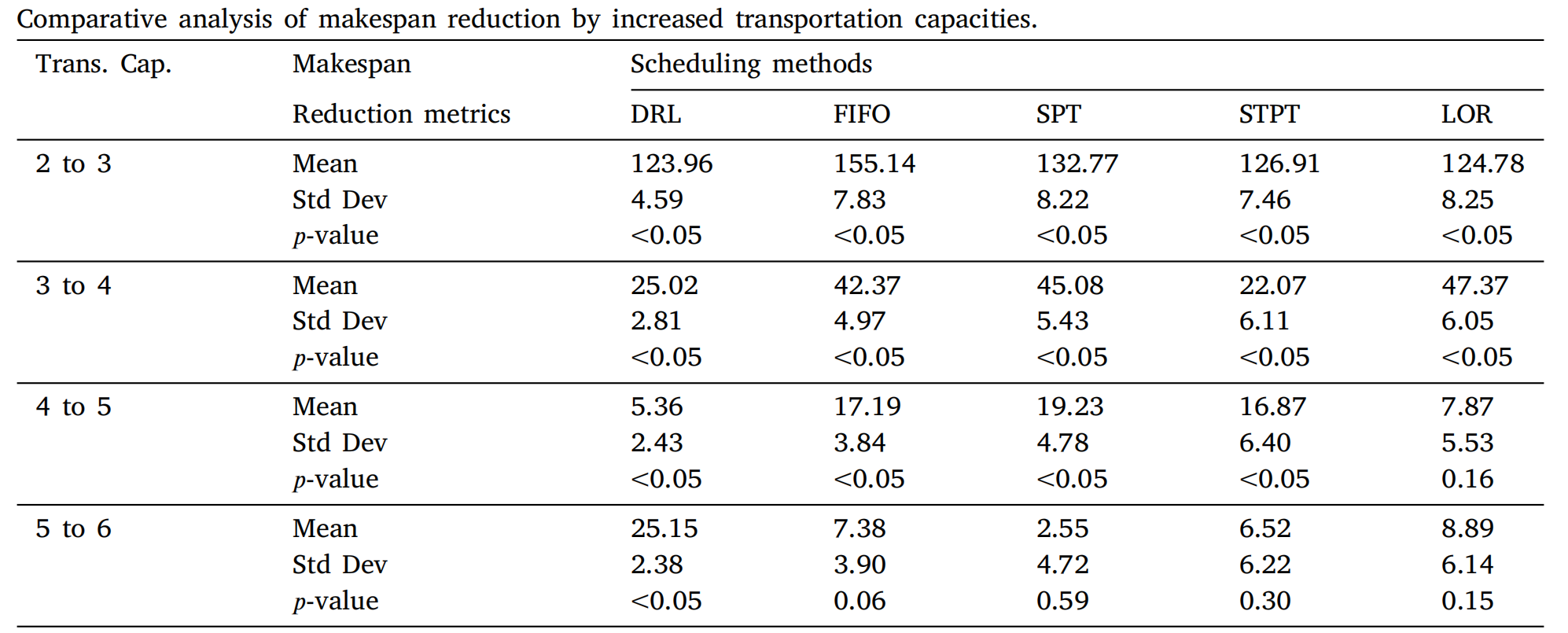
进一步通过配对t检验分析运输能力增加对完工时间的影响。在上表中，均值和标准差表示运输能力增加导致的完工时间减少的均值和标准差。从结果可以看出，当运输能力小于4时，p值始终低于0.05，通过增加容量可以实现统计上显著的完工时间减少。然而，当运输能力达到4时，对完工时间和系统效率的影响变得不太显著。这是因为系统已经拥有足够的运输能力来运行，不受缓冲区的限制，因此增加容量不会显著提高其性能。

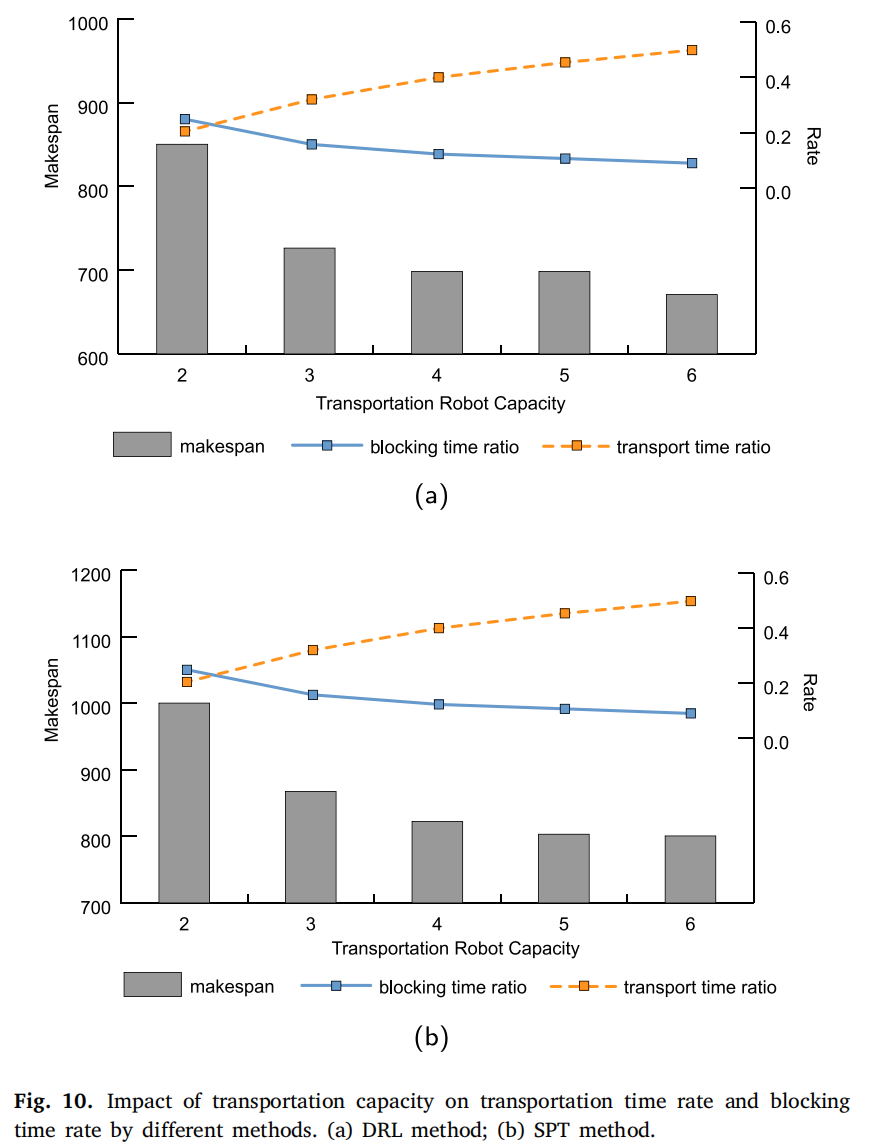
此外，图10深入探讨了随着运输能力增加，机器上的阻塞时间和机器人的运输时间的变化。这里的讨论围绕机器上的阻塞时间比率$(r_{blocking})$和运输机器人上的运输时间比率$(r_{trans})$。$r_{blocking}$表示作业在机器上被阻塞的时间占作业在制造系统中总时间的比例。当作业完成处理但仍未被运输并占用机器时，就会发生机器上的阻塞时间。另一方面，$r_{trans}$表示作业由运输机器人运输的时间占作业在制造系统中总时间的比例。

如图10所示，通过增加运输机器人的能力，可以减少完工时间和阻塞时间比率。随着运输能力的提高，作业在运输机器人上花费的时间比例显著增加，同时减少了机器上的阻塞时间。这种运输能力的增强通过在运输机器人上存储更多作业来提高机器利用率，减轻作业在机器上的阻塞，从而提高整体处理效率。然而，随着容量的持续增加，作业在机器上的阻塞时间比例接近零，这表明随着运输能力的提高，对生产线的优化效果接近饱和。