前言

  最短路径的题单可以刷 灵茶山艾府 的题单 分享丨【题单】图论算法（DFS/BFS/拓扑排序/最短路/最小生成树/二分图/基环树/欧拉路径）。关于这三种算法的一些可视化视频讲解可以查看文末的参考文献，本文是这些分享的学习笔记。

Dijkstra 算法 的核心思想：

• 每次从还未遍历的节点中选择路径最短的一个节点遍历。
• 更新与该节点相邻的节点的最短路径值。
• 当所有节点都被遍历完毕，或者剩余的未遍历的节点的最短路径为无穷大，那么算法结束。

Dijkstra 算法

  Dijkstra 算法用于求一个 非负权图 里一个结点到任意节点的最短距离，也可以求这个最短距离的路径，它由荷兰计算机科学家狄克斯特拉（Dijkstra）于1959年提出。
  Dijkstra 算法的核心思想就是：采用 贪心 的策略，每次从还未遍历的节点中选择路径最短的一个节点进行遍历，更新与该节点相邻的节点的最短路径值，直到所有的节点都被遍历完毕。

Dijkstra 算法的一般步骤

1. 将题目中的信息转化为一个带权图 $G=(V,E)$，起始点 $s\in V$，任意一条边的权值 $w(u,v)\ge 0$，当点 $u$ 和点 $v$ 之间不存在边时，定义 $w(u,v)=+\infty$。
2. 初始化数组

• 用一个数组 $dis[i]$ 来记录节点 $s$ 到节点 $i$ 的最短距离，初始化 $dis[s]=0$，其余的节点： $dis[i]=+\infty$。
• 用一个数组 $vis[i]$ 来记录节点 $i$ 是否已经遍历，初始化所有 $vis[i]=false$，表示节点 $i$ 还没有遍历。
• 用一个数组 $par[i]$ 来记录每一个节点最优路径的前一个节点，初始化所有的 $par[i]=-1$，表示没有前一个节点。如果不需要求具体的路径，那么就不需要该数组。

3. 定义节点 $u=s$, 从节点 $u$ 开始遍历图 $G$:

• 如果 $vis[u]=true$，说明该节点已经遍历，执行下一步。否则：更新节点 $u$ 的所有相邻节点 $v$ 的最短路径 $dis[v]$，此时从节点 $s$ 到节点 $u$ 的路径为 $dis[u]$，从节点 $u$ 到节点 $v$ 的路径为 $w(u,v)$，那么从节点 $s$，经过节点 $u$ 到节点 $v$ 的路径为 $d=dis[u]+w(u,v)$，如果 $d\le dis[v]$，说明这条路径更优，将 $dis[v]$ 更新为 $d$。如果要记录路径，则更新 $par[v]=u$。
• 将节点 $u$ 设置为已经遍历：$vis[u]=true$。从所有 $vis[i]=false$ 的节点 $i$ 中选择 $dis[i]$ 最小的节点 $j$，将 $u$ 更新为 $j$，重复上一步。如果所有的节点都已经遍历，或者 $dis[j]=+\infty$，则算法结束。

Dijkstra 算法的执行过程（一个例子）

  为了更直观的理解 Dijkstra 算法的整个具体流程，下面用一个例子来具体演示 Dijkstra 算法的执行过程^[1]

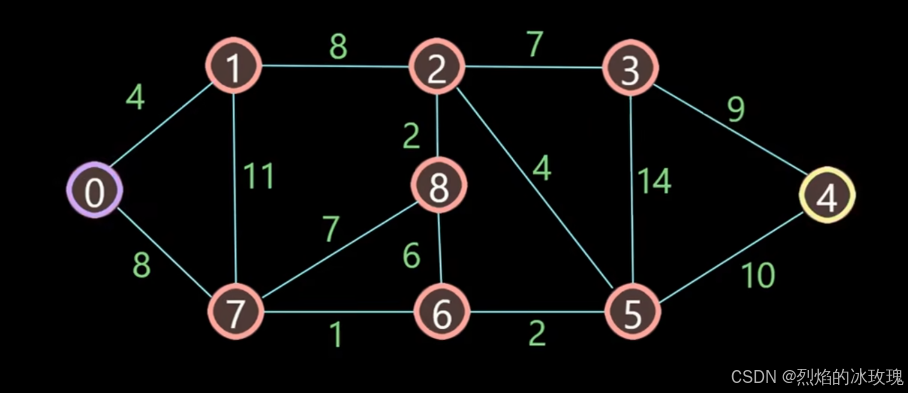
  第一步，得到一个带权的图 $G$，假设这个图如下图所示，一共有 0 到 8 共 9 个节点：
 
 
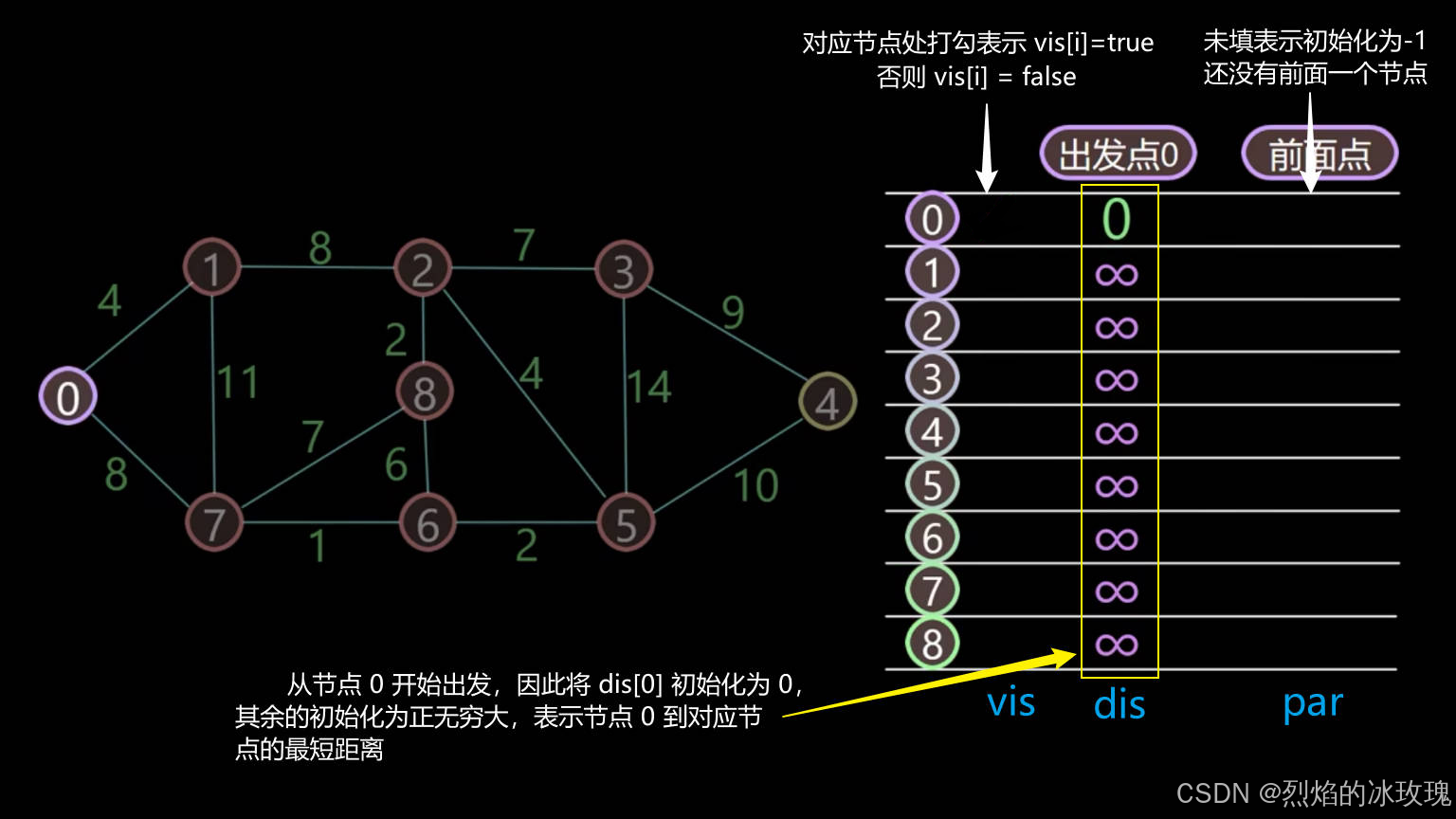
 第二步，初始化辅助数组，此时 $dis[i]=+\infty$，$dis[0]=0$；$par[i]=-1$；$vis[i]=false$：
 

 
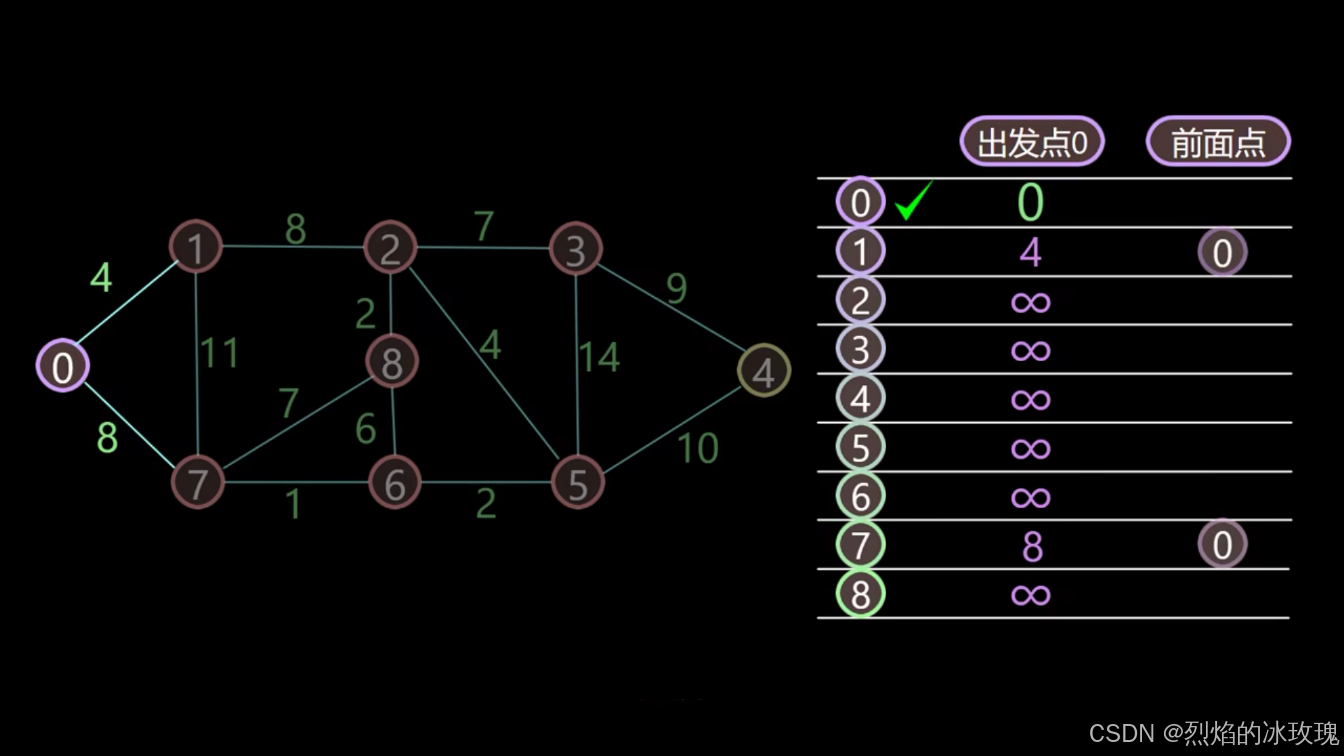
 第三步，遍历当前的节点，当前的节点为节点 0，更新 $vis[i]=true$。此时与节点 0 相邻的节点是节点 1 和 节点 7。节点 0 到节点 1 的距离为 4，$4<dis[1]=+\infty$，因此更新 $dis[1]=dis[0]+w(0,1)=0+4=4$，同时更新它的前面一个节点为节点 0，即更新 $par[1]=0$；同样的，对于节点 7，更新 $dis[7]=dis[0]+w(0,7)=0+8=8$，$par[7]=0$:
 

 
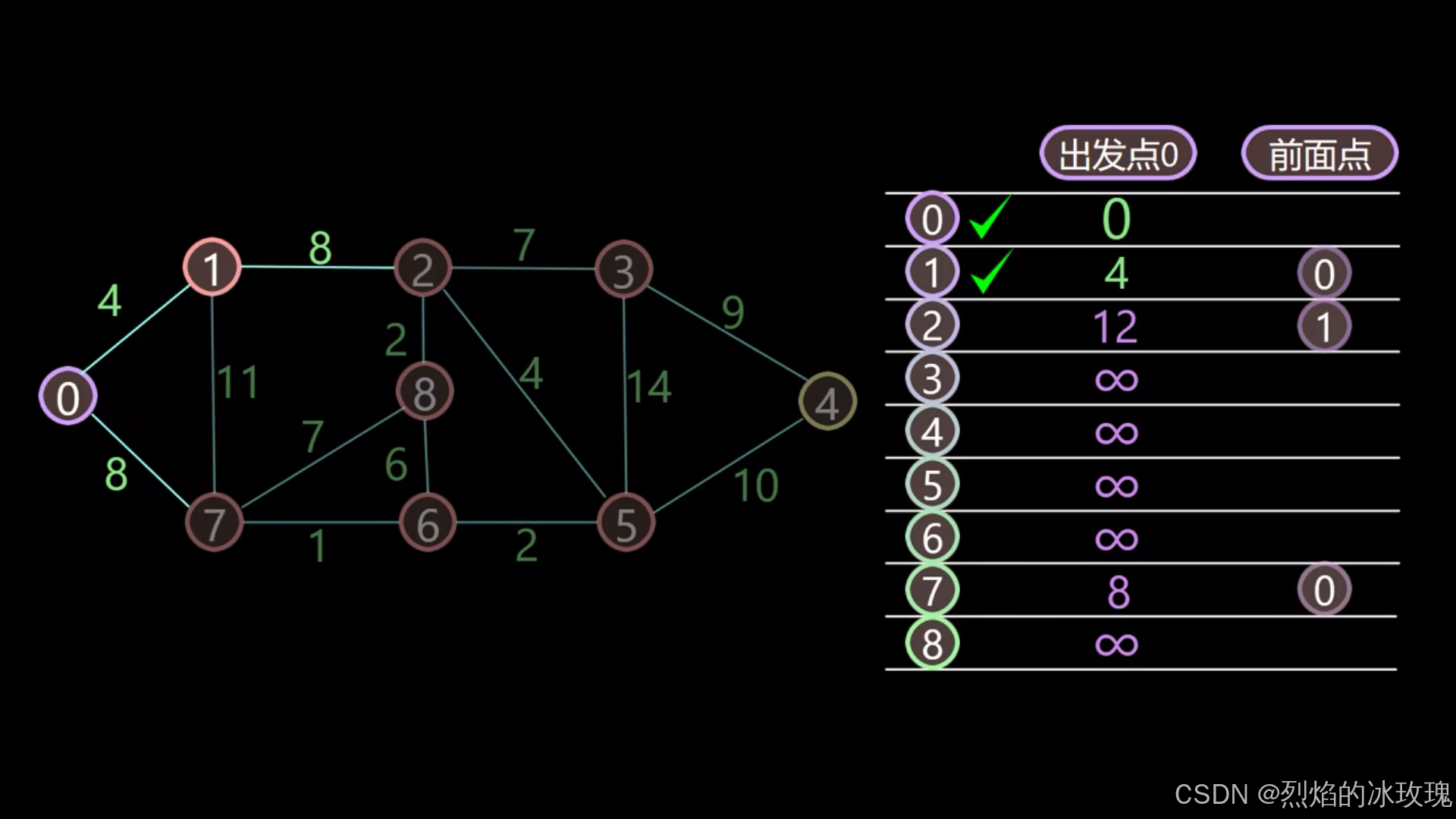
  接下来从 还未遍历的节点 $i$ 中选择 $dis[i]$ 最小的一个节点，此时是节点 1， 他的距离为 $dis[1]=4$，更新 $vis[1]=true$，将节点 1 作为当前的节点，重复上一步：
 
  遍历节点 1，此时与节点 1 相邻的节点是节点 2 和节点 7。对于节点 2，经过节点 1 的最短路径距离为 $dis[1]+w(1,2)=4+8=12<dis[2]=+\infty$，因此更新 $dis[2]=12$，$par[2]=1$；对于节点 7，经过节点 1 的最短路径距离为 $dis[1]+w(1,7)=4+11=15>dis[7]=8$，因此不进行更新。
 

 
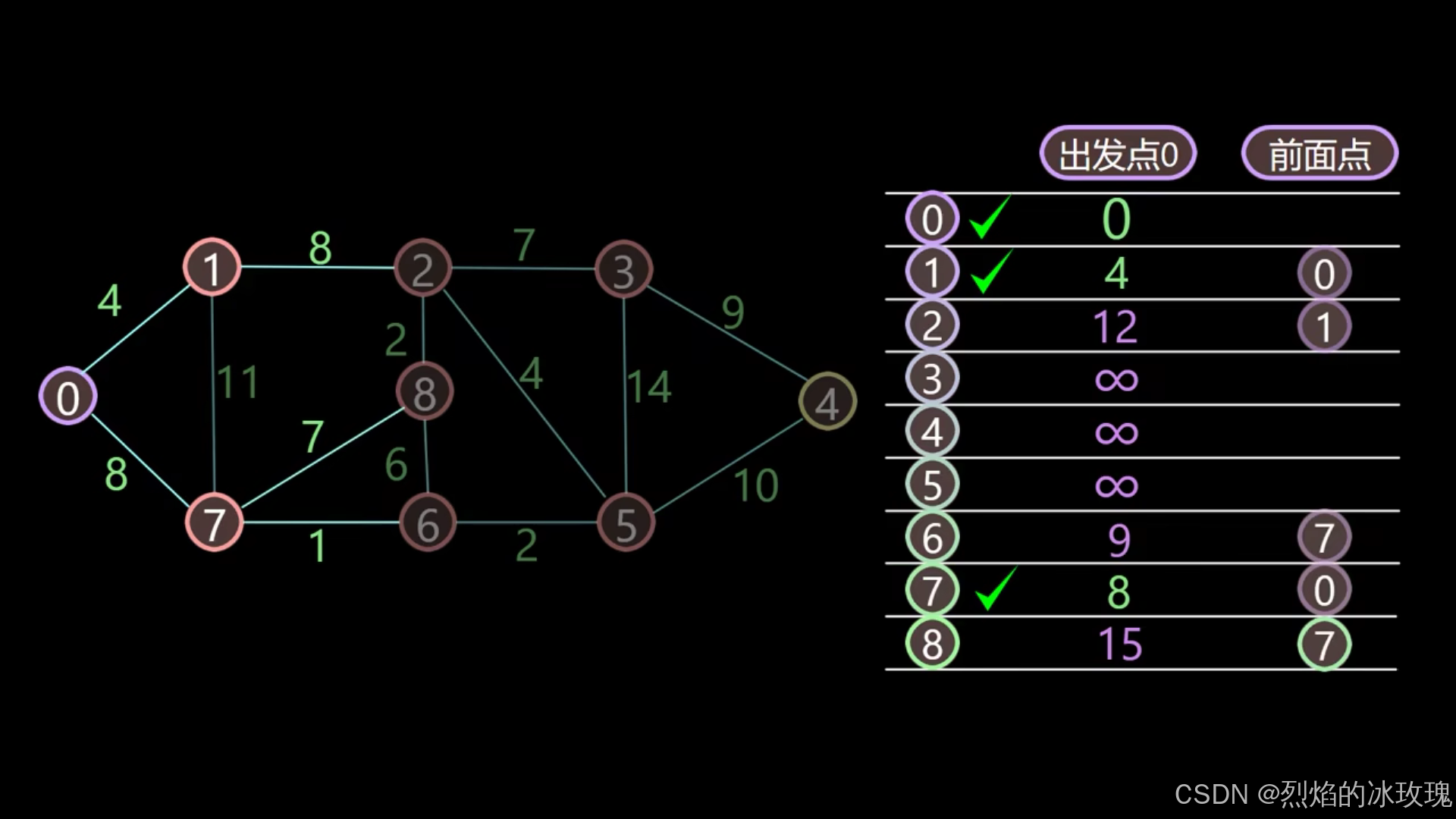
  之后的步骤就和前面的类似，未遍历的节点中最短距离最小的是节点 7，因此遍历节点 7，更新其对应的相邻节点，节点 6 和节点 8：
 

 
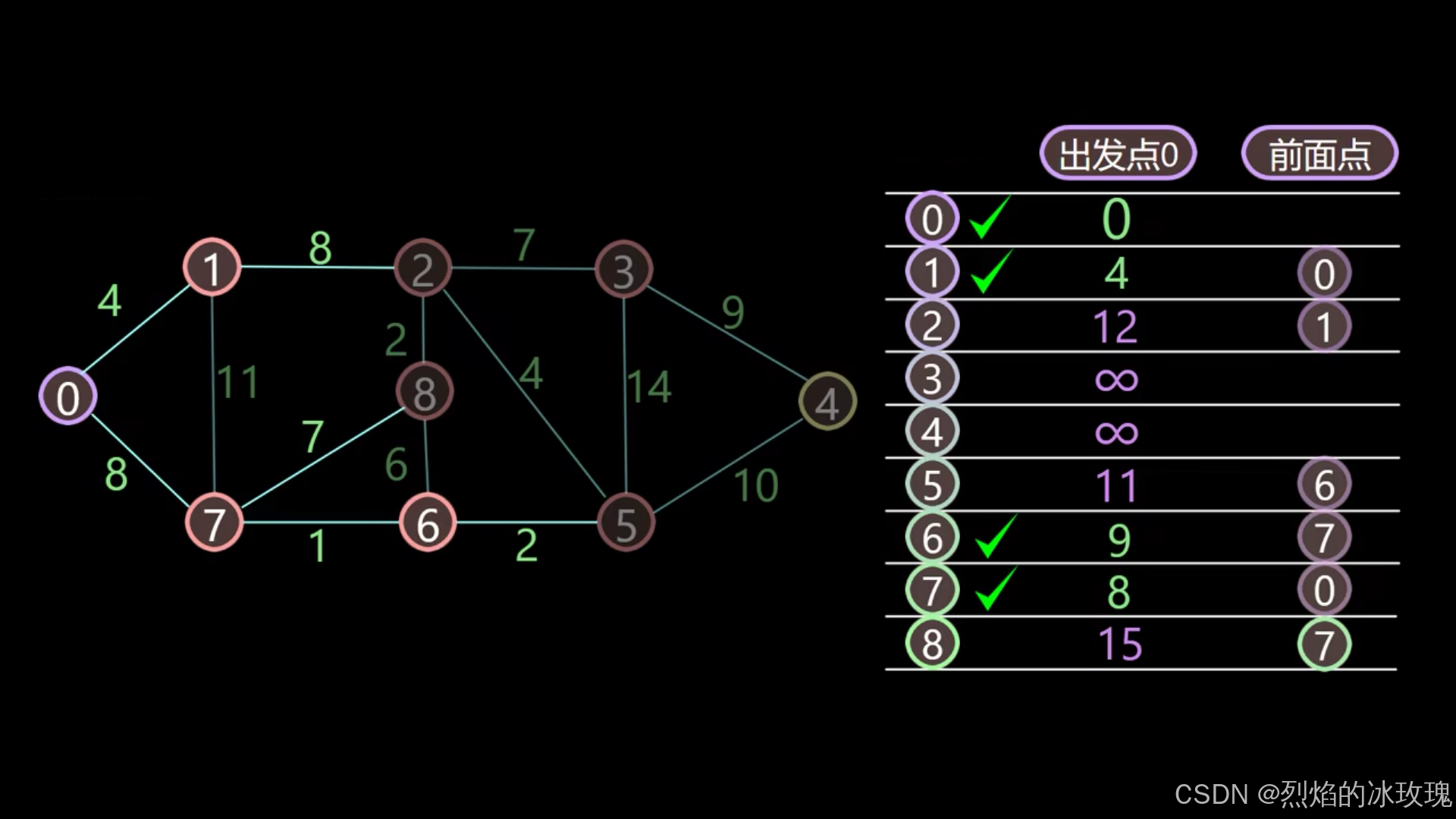
  遍历节点 6：
 

 
  遍历节点 5：
 

 
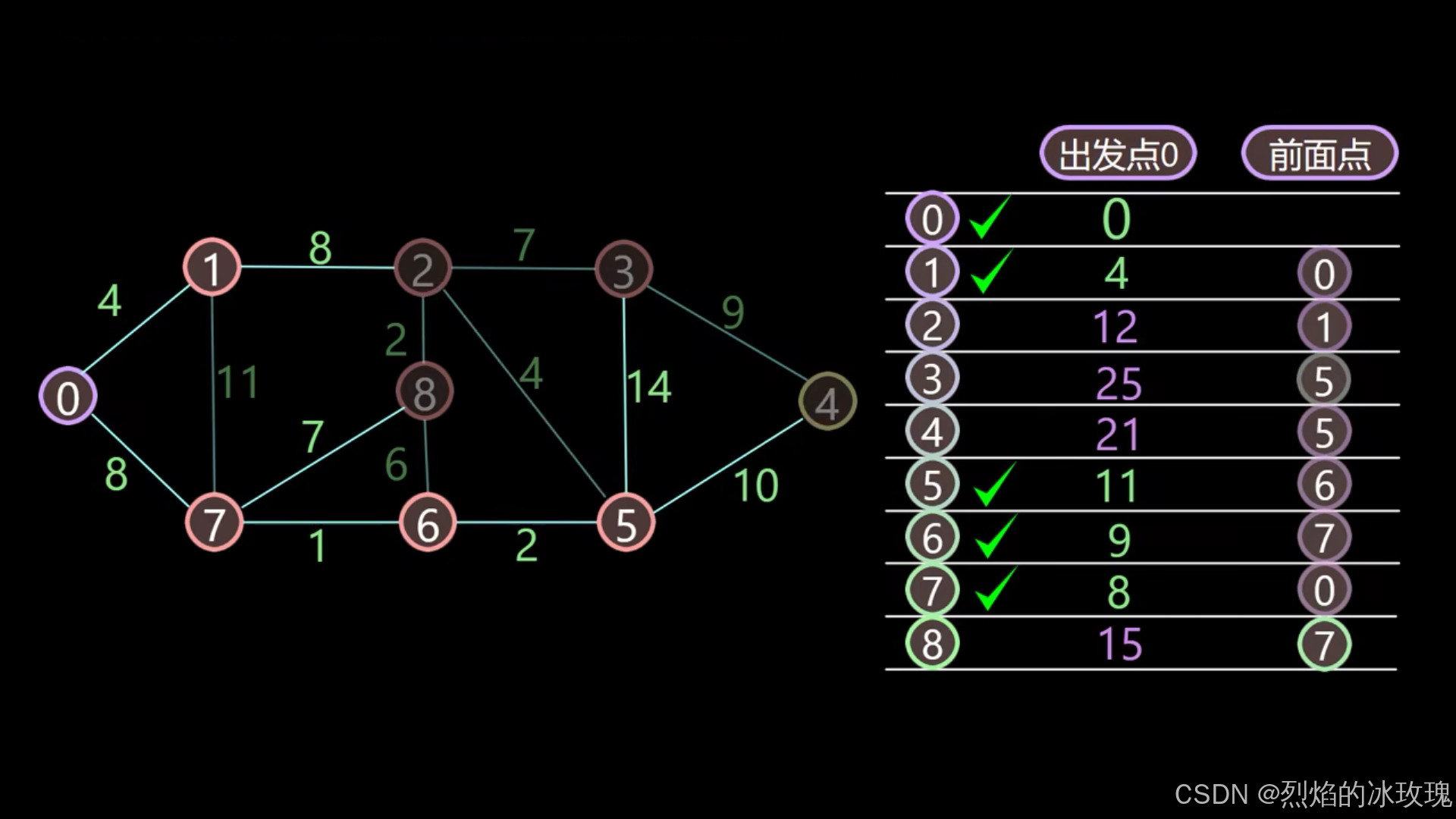
  遍历节点 2：
 

 
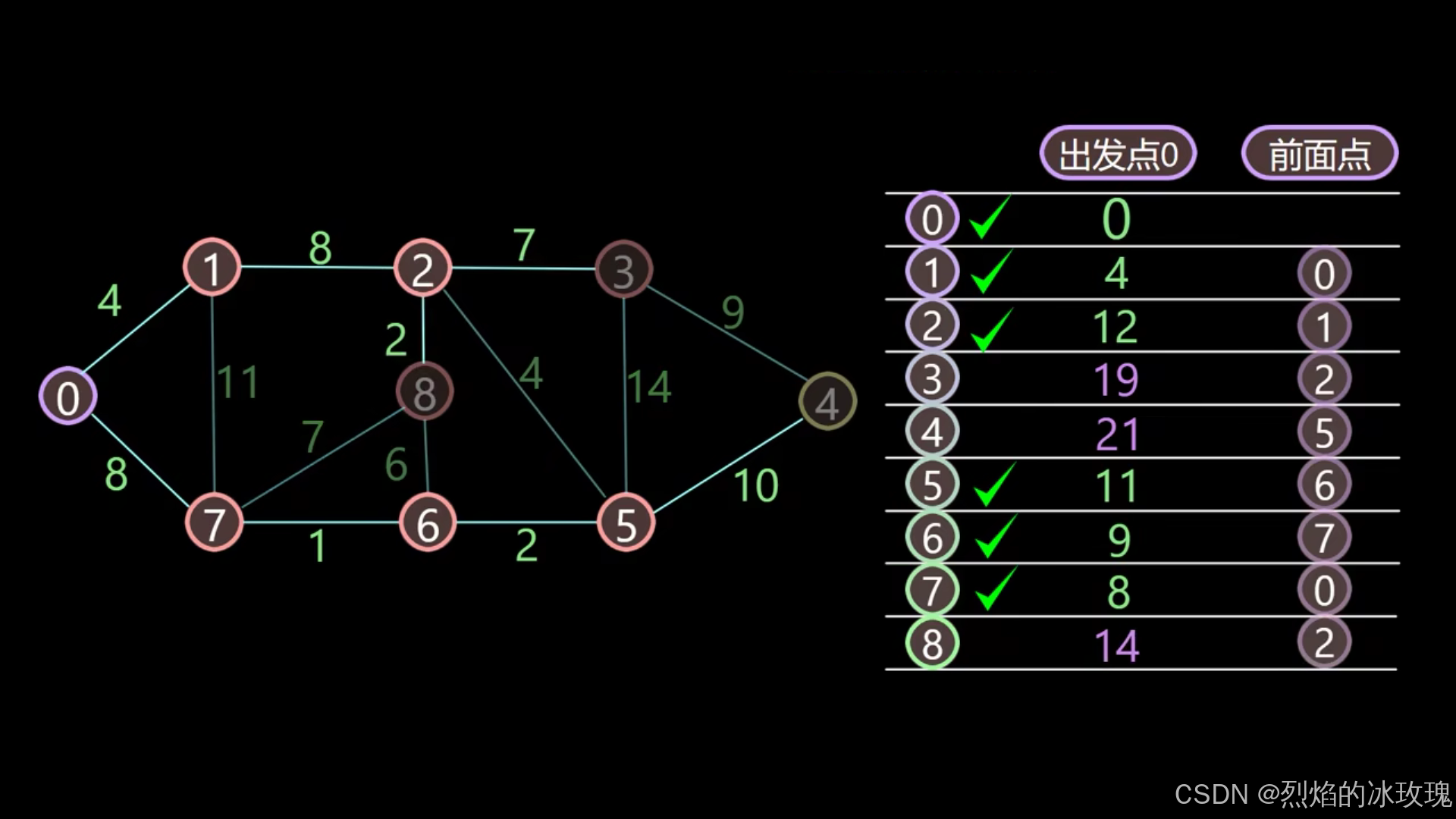
  遍历节点 8：
 

 
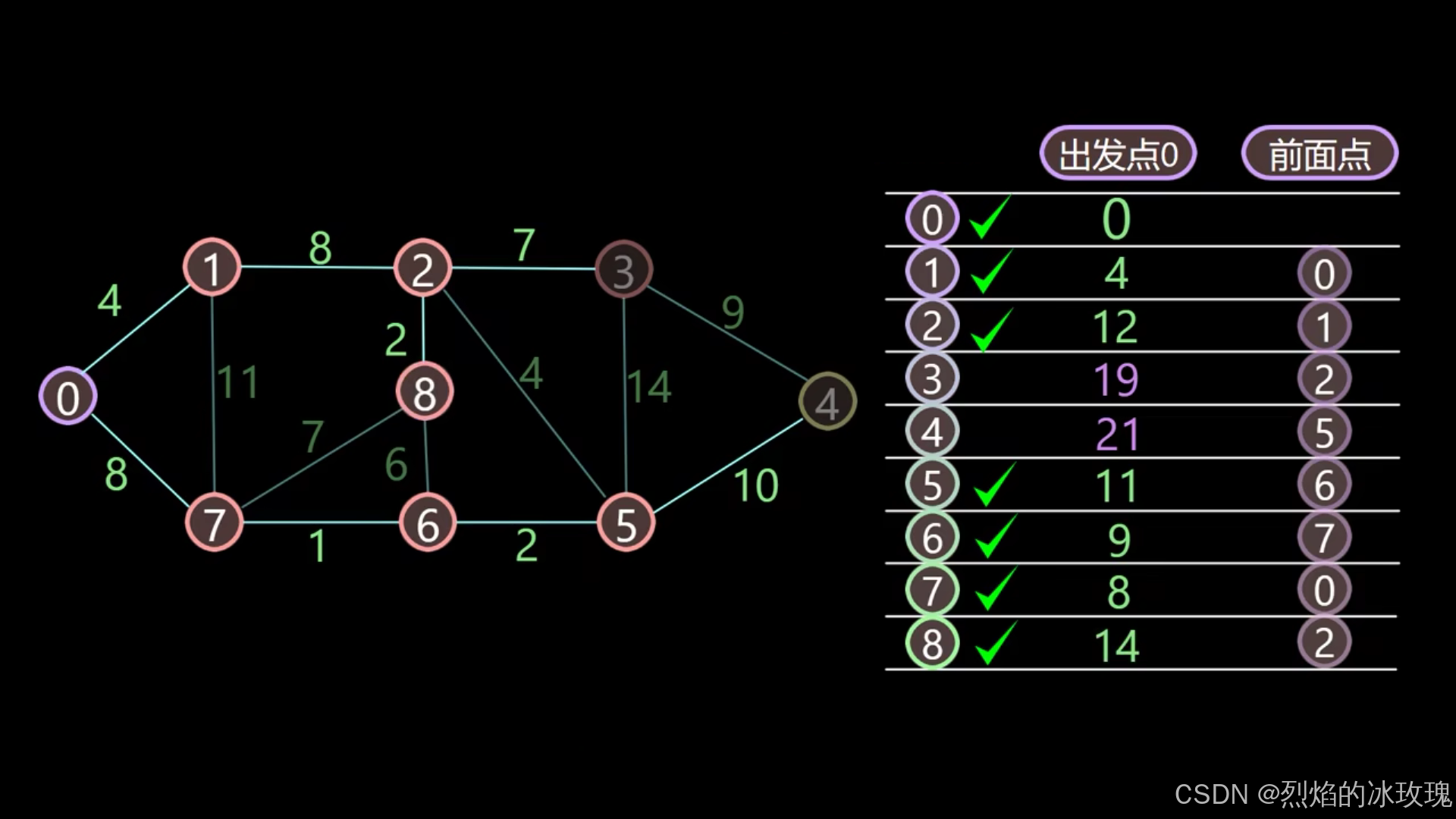
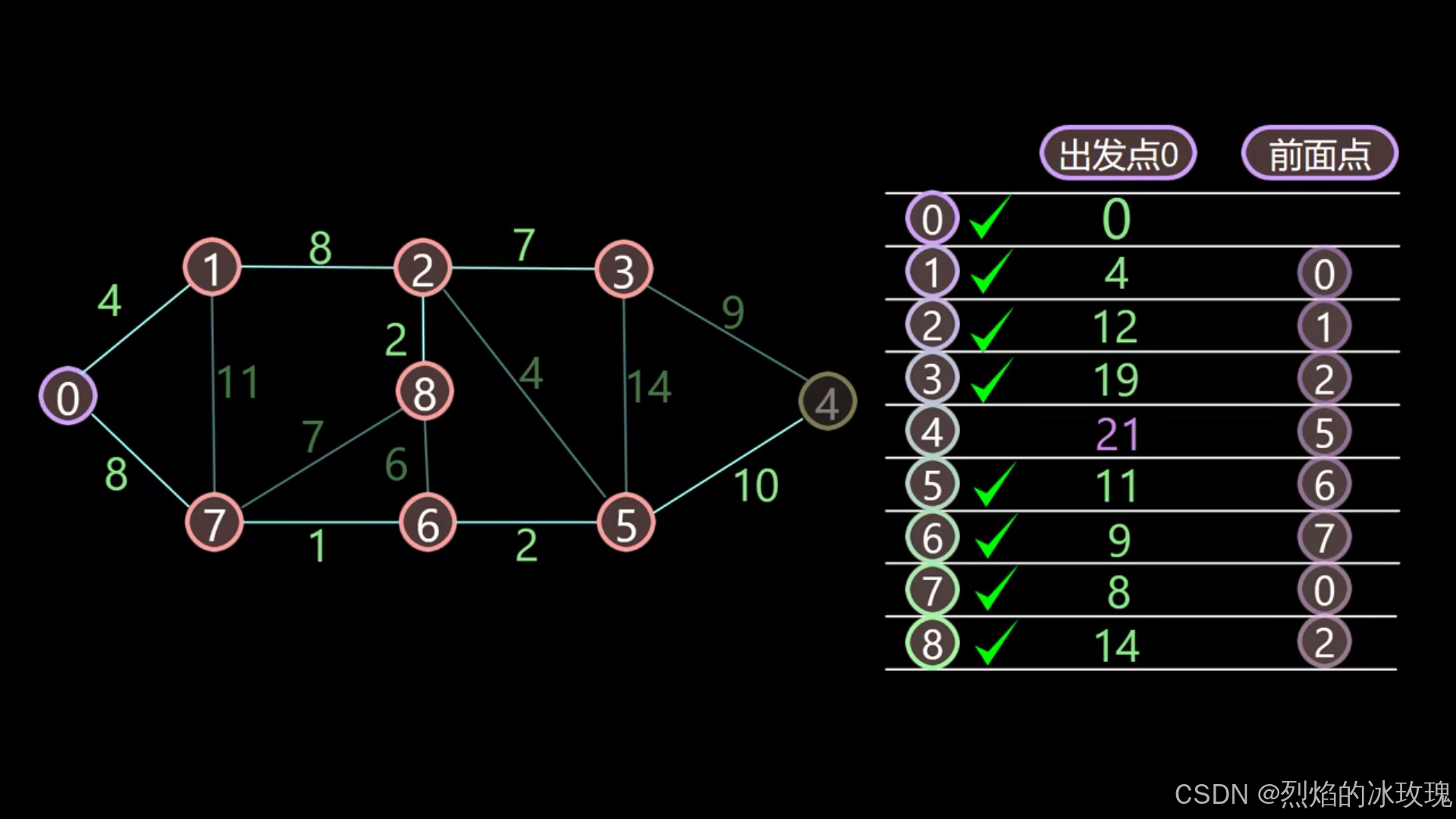
  遍历节点 3：
 

 
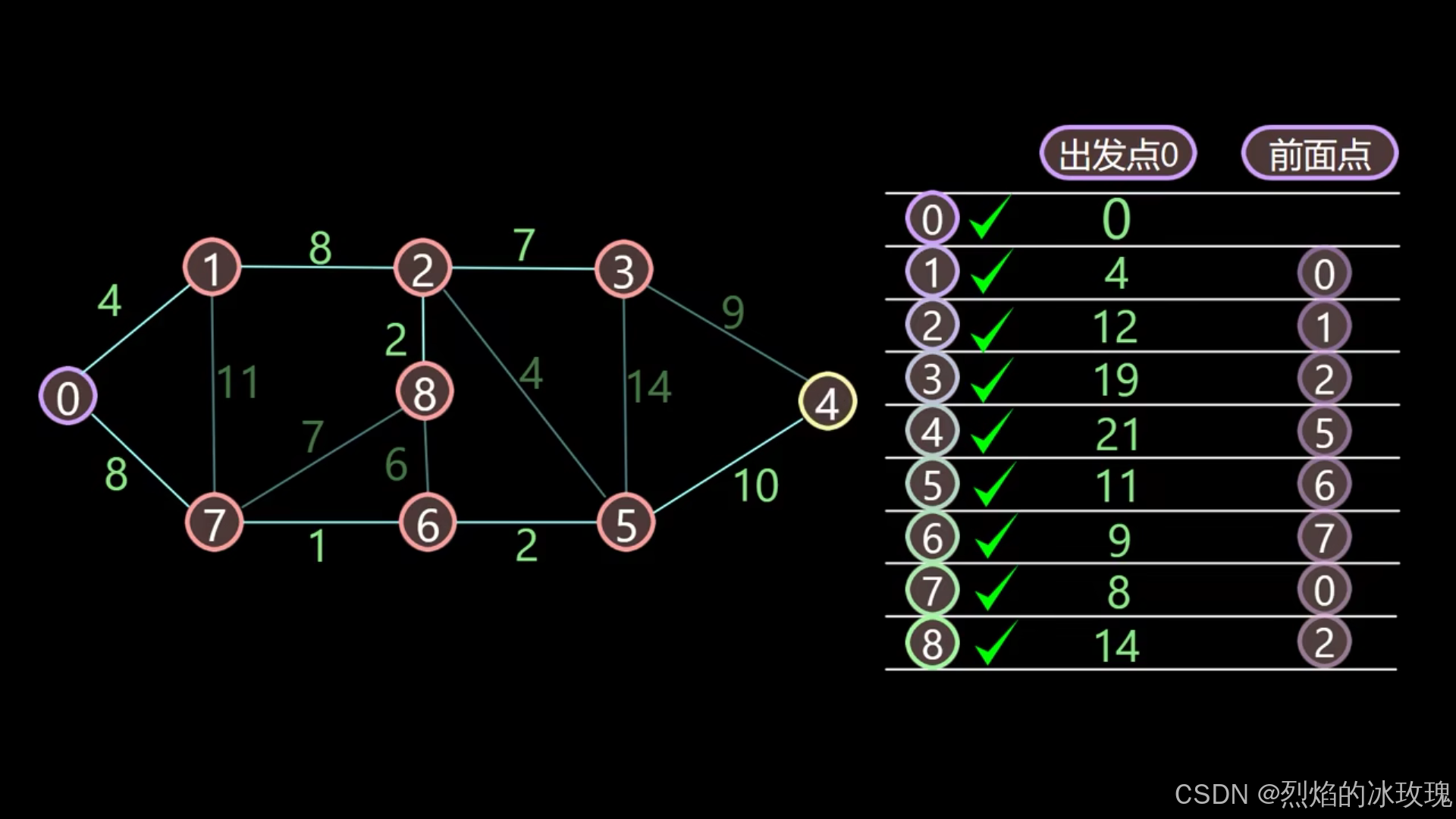
  遍历节点 4：
 

 
  此时所有的节点都已经更新完毕，算法结束。
 
注：本案例图片来自于参考文献处的链接视频。

Dijkstra 算法的具体步骤及代码实现

  对于稠密图和稀疏图，Dijkstra 算法有两种不同的实现方式。对于稠密图，一般会采用邻接矩阵来进行存储；而对于稀疏图，则一般采用邻接表来进行存储。

输入描述：

• 一组带权值的边（这里以有向边为例，无向边可以当作两条有向边处理）vector<vector<int>> egdes: 其中 egdes[i] = [u, v, w]，表示节点 u 到节点 v 有条权值为 w 的边；
• n 表示一共有 n 个节点，编号为 0 到 n;
• start 表示要求从 start 节点到各个节点的最短距离。

输出描述：

• 输出一个长度为 n 的数组 dist， dist[i] 表示从节点 start 到节点 i 的最短距离。

求解稠密图

vector<int> dijkstraByDenseGraph(vector<vector<int>>& edges, int n, int start){
	//建图（用邻接矩阵存储）
    vector<vector<int>> graph(n, vector<int>(n, INT_MAX));
    for(auto &edge:edges){
        graph[edge[0]][edge[1]] = edge[2];
    }

	//数组初始化
    vector<int> dis(n, INT_MAX);
    dis[start] = 0;
    vector<bool> vis(n, false); 
    vector<int> par(n, -1);

    while(true){
        int u = -1, d = INT_MAX;
        //选择当前未遍历节点中距离最小的节点遍历
        for(int i=0;i<n;++i){
            if(!vis[i] && dis[i]<d){
                d = dis[i];
                u = i;
            }
        }

        if(u==-1) break;  //所有能遍历的节点都遍历完
        vis[u] = true;

        //更新节点 u 的所有相邻节点
        for(int v=0;v<n;++v){
            if(graph[u][v]!=INT_MAX && d+graph[u][v] < dis[v]){
                dis[v] = d+graph[u][v];
                par[v] = u;
            }
        }
    }

    return dis;
}

时间复杂度分析：
  在 while 循环中，每次会更新一次 vis，一共有 n 个节点，最多进行 n 次 while 循环。每一次 while 循环中，求当前最短路径的节点需要 $O(n)$ 的时间复杂度，更新节点 u 的所有相邻节点需要 $O(n)$ 的时间复杂度，因此总共的时间复杂度是 $O(n^2)$

空间复杂度分析：
  需要 $O(n^2)$ 的邻接表和若干个 $O(n)$ 的辅助矩阵，总的空间复杂度是 $O(n^2)$ 的。

求解稀疏图

vector<int> dijkstraBySparseGraph(vector<vector<int>>& edges, int n, int start){
	//建图（用邻接表来存储）
    vector<vector<pair<int,int>>> graph(n);
    for(auto& edge:edges){
        graph[edge[0]].emplace_back(edge[1], edge[2]);
    }
	
	//初始化数组
    vector<int> dis(n, INT_MAX); //dis[i] 记录节点 i 到节点 start 的最短距离
    dis[start] = 0;
    vector<bool> vis(n, false);  //vis[i] 记录节点 i 是否已经遍历
    vector<int> par(n, -1);      //如果题目不需要求最短路径，只求长度，则不需要记录该数组

	//使用最小堆优化求解为遍历节点最小值的过程
    priority_queue<pair<int,int>, vector<pair<int,int>>, std::greater<>> pq;

    pq.emplace(0, start);        //首先加入start节点
    while(!pq.empty()){
        //选择当前未遍历节点中距离最小的节点
        auto [d, u] = pq.top();  
        pq.pop();
        if(vis[u]) continue;     
        vis[u] = true;           

        //更新该节点的所有相邻节点
        for(auto &[v, w]:graph[u]){
            if(d+w<dis[v]){
                pq.emplace(d+w, v);
                dis[v] = d+w;
                par[v] = u; //如果不需要求路径则不需要更新此处
            }
        }
    }

    return dis;
}

注：

• 不需要判断当前遍历的节点的最短距离是否是 $+\infty$，因为从节点 start 开始遍历，只有更新的距离小于 $+\infty$ 才会加入到优先队列中，所以优先队列中的所有节点都一定可达。
• 在更新节点 u 的所有相邻节点 v 时，不需要判断节点 v 是否已经遍历，因为如果节点 v 已经遍历，那么 dis[v] 就是最优值，d+w 不可能比 dis[v] 还小，因此如果能够更新，那么节点 v 一定未遍历（但有可能 dis[v] 被更新过了，此时能够加入优先队列重新更新）。

一个优化：

  可以不使用 vis 数组来记录节点是否已经遍历：将

if(vis[u]) continue;     
vis[u] = true;

  更改为：

if(d>dis[u]) continue;  

  因为 d 是剩余所有最短路径的最小值，就意味着后续对节点 u 的更新不可能比 d 还小，那么此时 d > dis[u] 表明 dis[u] 已经是最优的，即节点 u 已经被遍历过。 求解稠密图也可以用类似的优化。

时间复杂度分析：

  对于每一个节点，最多只会被遍历一次，而对于每一条边，至多加入到优先队列中一次，优先队列中最多有 $m$ 个元素，每次从优先队列中取出距离最短的节点的操作复杂度为 $O(logm)$。因此算法的时间复杂度为 $O(mlogm)$，$m$ 为边的条数。
  如果输入的是一个稠密图，那么 $m\sim n^2$，那么该方法的时间复杂度为 $O(n^{2}logn)$。

空间复杂度分析：
  $O(n+m)$ ：需要长度为 $n$ 的辅助数组，$graph$ 中一共存储的边的条数为 $m$ 条。

Dijkstra 算法的正确性证明

目标：证明算法结束时，$d(v)$ 为 $s$ 到 $v$ 的最短路径长度。

证明：
  采用 数学归纳法 和 反证法。
归纳假设：
  假设前 $k$ 个已遍历顶点 $u_1,u_2,u_3,...,u_k$ 满足 $d(u_i)$ 是最短路径长度。
基础情况：
  $d(s)=0$， 是最短路径长度，只有这个节点已遍历。
归纳递推：
  现在我们要处理第 $k+1$ 个节点 $u_{k+1}$，它是剩余未遍历节点中 $d(u)$ 最小的一个节点。此时
$$d(u_{k+1})=\underset{0\le i\le k}{\min }(d(u_i)+w(u_i,u_{k+1}))，vis(u_i)=true.$$
  它是只经过所有已遍历节点的从 $s$ 到 $u_{k+1}$的最短路径。
  反证： 假设 此时的 $d(u_{k+1})$ 不是最优解。
  那么最优解一定要经过一个未曾遍历过的节点 $v$，然后再经过若干距离才能到达 $u_{k+1}$。设这条路径中第一个未曾遍历的节点为 $v_0$，从点 $s$ 出发（$vis(u_i)=true$），经过顶点 $v_0$，再经过路径 $y$ 到达节点 $u_{k+1}$，那么有
$$betterDis=d(v_0)+y$$
  由于路径中没有负权值，因此 $y>0$，而 $d(u_{k+1})$ 是还未遍历的节点中的最小距离，因此 $d(u_{k+1})<d(v_0)$，所以 $betterDis>d(u_{k+1})$。
  因此不存在这样的路径，与假设矛盾。所以此时的 $d(u_{k+1})$ 是最优解。
  而如果图中存在负权值的边，那么 $d(u_{k+1})>d(v_0)+y$ 就有可能成立，因此 Dijsktra 算法无法处理边为负权值的图。

Bellman-Ford 算法

  如果边存在负权值，那么 Dijkstra 将不再适用，此时求单源最短路径可以采用 Bellman-Ford 算法。如果图中存在 负权环, 而且从起点可以抵达负权环，那么从起点到任意节点的 最短路径 不存在，因为可以不断地在这个负权环中循环，使得路径无限地减小下去。使用 Bellman-Ford 算法可以检测 负权环是否存在 。
  Bellman-Ford 算法由 Alfonso Shimbel 在 1955 年首次提出，由 Richard Bellman 和 Lester Ford Jr, 分别于 1958 和 1956 年发表。Edward F.Moore 也在 1959 年发表了该算法的变体，因此有时也称为 Bellman–Ford–Moore 算法。
   Bellman-Ford 算法的核心思想是：遍历所有的边，对每一条边连接的节点，更新通过该边后源节点到该节点的最短距离， 执行 $|V|-1$ 轮操作，或者一轮操作中不再有节点被更新，表示所有的最短路径都被找到。最后遍历一次所有的边，如果此次遍历中有顶点更新，那么说明存在可以从源节点抵达的负权环，算法不会收敛。
  每次遍历一条边执行的操作称为对这一条边进行了一次 松弛操作（relaxation），$|V|$ 表示图中的顶点个数。

Bellman-Ford 算法的一般步骤

1. 得到图顶点的个数 n, 边集 edges，起始点 start。
2. 初始化数组：

• 初始化长度为 n 的数组 distance 用来表示从起始点到每一个节点的最短路径长度。其中 distance[start] = 0, 表示起始点到起始点的代价为 0，其余节点初始为 INF。
• 初始化长度为 n 的数组 predecessor 用来表示每一个顶点的最短路径的前驱节点。初始化所有点的前驱节点为 NULL，或者用 -1 来表示 NULL。

3. 对所有有向边进行 $|V|-1$ 轮 松弛 操作：

• 对于边 (u, v, w)，如果 distance[u] + w < distance[v]，表示一条更短的路径被找到了，更新 distance[v] = distance[u] + w， predecessor[v] = u, 记录到点 v 的最短路径和前驱节点。
• 当当前轮的所有边遍历完成后，如果没有任何一个顶点被更新，说明所有的最短路径都已经被找到，可以提前退出循环。

4. 如果执行了 $|V|-1$ 轮操作过程中，没有提前退出循环，那么需要再对所有边进行一次 松弛 操作：

• 如果在这次循环中还有边可以被更新，那么说明图中存在负权环，算法无法找到最短路径。
• 如果需要找到父权环，我们需要根据此时被更新的顶点的前驱节点往前进行遍历，当找到一个在此次遍历中已经遍历过的节点，这个节点就在负权环中。

下面是 Bellman-Ford 算法的伪代码实现，展示了它执行的一般步骤^[3] :

function BellmanFord(list vertices, list edges, vertex source) is

    // This implementation takes in a graph, represented as
    // lists of vertices (represented as integers [0..n-1]) and
    // edges, and fills two arrays (distance and predecessor)
    // holding the shortest path from the source to each vertex

    distance := list of size n
    predecessor := list of size n

    // Step 1: initialize graph
    for each vertex v in vertices do
        // Initialize the distance to all vertices to infinity
        distance[v] := inf
        // And having a null predecessor
        predecessor[v] := null
    
    // The distance from the source to itself is zero
    distance[source] := 0

    // Step 2: relax edges repeatedly
    repeat |V|−1 times:
        for each edge (u, v) with weight w in edges do
            if distance[u] + w < distance[v] then
                distance[v] := distance[u] + w
                predecessor[v] := u

    // Step 3: check for negative-weight cycles
    for each edge (u, v) with weight w in edges do
        if distance[u] + w < distance[v] then
            predecessor[v] := u
            // A negative cycle exists;
            // find a vertex on the cycle
            visited := list of size n initialized with false
            visited[v] := true
            while not visited[u] do
                visited[u] := true
                u := predecessor[u]
            // u is a vertex in a negative cycle,
            // find the cycle itself
            ncycle := [u]
            v := predecessor[u]
            while v != u do
                ncycle := concatenate([v], ncycle)
                v := predecessor[v]
            error "Graph contains a negative-weight cycle", ncycle
    return distance, predecessor

Bellman-Ford 算法的执行过程（一个例子）

  为了更直观的理解 Bellman-Ford 算法的整个具体流程，下面用一个例子来具体演示 Bellman-Ford 算法的执行过程^[4]

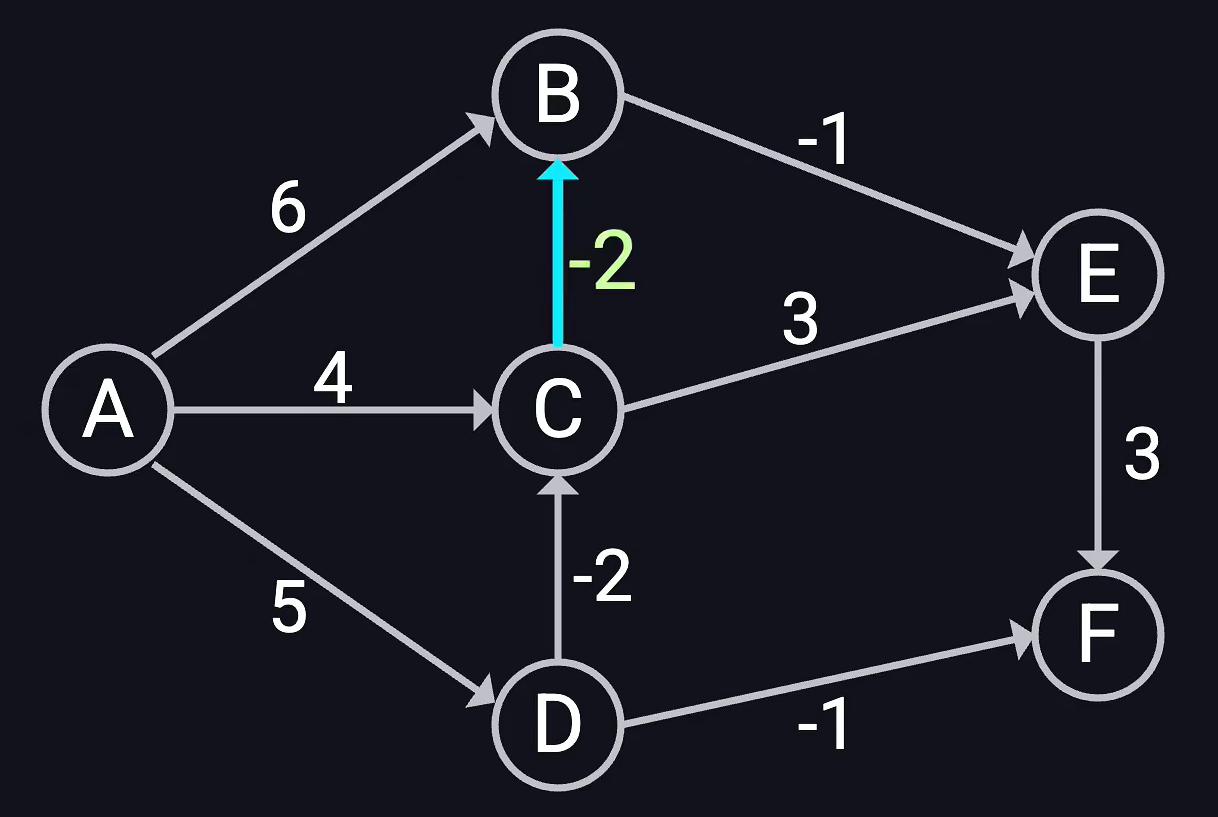
  第一步，得到一个带权的图 $G$，假设这个图如下图所示，一共有 A 到 E 共 6 个节点，求点 A 到各个顶点的最短距离：
 
 
 第二步，初始化辅助数组，此时 $distance[i]=+\infty$，$distance[A]=0$；$predecessor[i]=-1$；
 
 第三步，对所有边执行 |V-1| 轮松弛操作，假设以 AB、AC、AD、BE、CB、CE、DC、DF、EF 的顺序进行遍历：
 第一轮

• 遍历 AB: distance[B] = min(distance[B], distance[A] + 6) = 6，predecessor[B] = A;
• 遍历 AC: distance[C] = min(distance[C], distance[A] + 4) = 4, predecessor[C] = A;
• 遍历 AD: distance[D] = min(distance[D], distance[A] + 5) = 5, predecessor[D] = A;
• 遍历 BE: distance[E] = min(distance[E], distance[B] - 1) = 5, predecessor[E] = B;
• 遍历 CB: distance[B] = min(distance[B], distance[C] - 2) = 2, predecessor[B] = C;
• 遍历 CE: distance[E] = min(distance[E], distance[C] + 3) = 5, predecessor[E] = B;
• 遍历 DC: distance[C] = min(distance[C], distance[D] - 2) = 3, predecessor[C] = D;
• 遍历 DF: distance[F] = min(distance[F], distance[D] - 1) = 4, predecessor[F] = D;
• 遍历 EF : distance[F] = min(distance[F], distance[E] + 3) = 4, predecessor[F] = D;

 
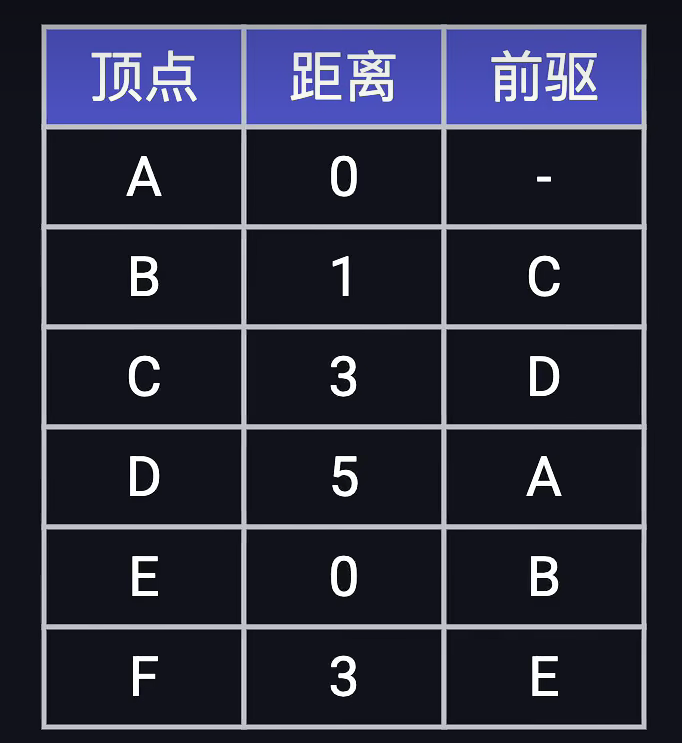
 重复 |V-1| 轮操作就可以得到最后的结果：
 

Bellman-Ford 算法的具体步骤及代码实现

输入描述：

• 给定具有 n 个顶点的图，图的边用二维数组 edges 表示，其中 edges[i] = (u,v,w) 表示一条从 u 节点到 v 节点的长度为 w 的有向边。

输出描述：

• 求从节点 node1 到节点 node2 的最短距离，如果不存在最短距离，输出 -1。

class Graph {
private:
    vector<vector<int>> edges;
    int n;
public:
    Graph(int n, vector<vector<int>>& edges) {
        this->n = n;
        this->edges = edges;
    }
    
    void addEdge(vector<int> edge) {
        edges.emplace_back(edge);
    }
    
    int shortestPath(int node1, int node2) {
        vector<int> distance(n, INT_MAX);
        vector<int> predecessor(n, -1);
        distance[node1] = 0;

        //进行 |V|-1 轮松弛操作
        for(int i=0;i<n-1;++i){
            bool updated = false;
            for(auto &edge:edges){
                int u = edge[0], v = edge[1], w = edge[2];
                if(distance[u]!=INT_MAX && distance[u]+w<distance[v]){
                    distance[v] = distance[u]+w;
                    predecessor[v] = u;
                    updated = true;
                }
            }
            if(!updated) break;
        }

        //检测是否有负权环
        for(auto &edge:edges){
            int u = edge[0], v = edge[1], w = edge[2];
            if(distance[u]!=INT_MAX && distance[u]+w<distance[v]){
                //存在负权环，算法不收敛
                vector<bool> vis(n, false);
                while(!vis[u]){
                    vis[u] = true;
                    u = predecessor[u];
                }
                cout<<"存在负权环，节点 "<<u<<" 是该负权环上的点"<<endl;
                return -1;
            }
        }

        return distance[node2]==INT_MAX?-1:distance[node2];
    }
};

Bellman-Ford 算法的正确性证明^[3]

目标：证明算法结束时，$d(v)$ 为 $s$ 到 $v$ 的最短路径长度。

证明：
  采用 数学归纳法。
归纳假设：
  假设第 $i$ 轮迭代后，$d(v)$ 表示从点 $s$ 到点 $v$ 最多经过 $i$ 条边的最小路径。
基础情况：
  第 $0$ 轮迭代，迭代还未开始，$d(s)=0$， 经过 $0$ 条边就可以到达节点 $0$，最短路径为 $0$， 其他节点经过 $0$ 条边不可以到达，故其他节点 $d[v]=+\infty$。
归纳递推：
  现在我们要处理第 $i$ 轮循环后的情况。对于第 $i-1$ 轮循环结束后，$d[v]$ 表示从节点 $s$ 到 $v$ 的最多经过 $i-1$ 条边的最短距离。我们用 $td[v]$ 表示从节点 $s$ 到 $v$ 的最多经过 $i$ 条边的最短距离，那么有：
$$td[v]=\min \left(d[v],\underset{(u,v)\in E}{\min }(d[u]+w(u,v))\right)$$
  相当于将所有的可能的情况都进行了枚举：所有可能的经过最多 $i-1$ 条边的情况，在此基础上多加一条边到达节点 $v$ 的情况，就是经过最多 $i$ 条边到达节点 $v$ 的情况。
  如果一条路径经过的边的数量大于等于 $|V|$，那么说明这条路径中存在环，且这个环一定是父权环，其中 $|V|$ 是图中顶点的数量。
  证明： 设这条带环的路径从节点 $s$ 出发，经过距离 $p1$ 到达环的入口 $in$，从 $in$ 节点经过距离 $p2$ 到 $in$ 节点出来，又经过 $p3$ 到达节点 $v$。
  总的距离 $d=p1+p2+p3$。
  如果不是负权环，那么 $p2>0$，$d_{min}=p1+p2$，这个结果应该由前面的 $d[v]$ 得到，因为这个路径最多用到的边更少。而一次循环中更新才会增加边的数量，在这次循环中要 $d[u]+w<d[v]$ 才会更新边，而 $d[v]$ 已经是从 $s$ 到 $v$ 中的所有路径中最小的，所有这种情况不会更新顶点。反之，如果更新顶点，那么这个环一定是负权环。
  因此，在迭代过程中，如果未更新任意一个顶点，那么就说明算法已经收敛。而在迭代了 $|V|-1$ 次之后，如果还能继续更新顶点，则说明图中存在负权环，算法不会收敛。
备注:
  在实际使用该算法的过程中，如果没有要求路径中边的数量限制，那么一般使用：
$$d[v]=\min \left(d[v],\underset{(u,v)\in E}{\min }(d[u]+w(u,v))\right)$$
  使得不存在负权环的图使用算法时能够更快地收敛，但是这样第 $i$ 轮循环中的 $d[v]$ 就不再是表示使用最多 $i$ 条边能够到达的最短距离了。

Floyd–Warshall 算法

  Floyd–Warshall 算法用于计算任意两点之间的最短距离。图中的边权值可以为负值，但是不能存在负权环。
  设一个图 $G$, 包含的节点为 $V$，节点编号为 $1$~$N$，用 $dist(i,j,k)$ 表示从节点 $i$ 到节点 $j$ 仅经过集合 { 1 , 2 , . . . , k } \{1,2,...,k \} {1,2,...,k} 中节点构成的路径中的最短路径长度，那么从 $i$ 点到 $j$ 点的最短路径就为 $dist(i,j,N)$。对于 $dist(i,j,k)$，可以得到下面的递推式：
$$dist(i,j,k)=\min (dist(i,j,k-1),dist(i,k,k-1)+dist(k,j,k-1))$$
  该递归式表示了不选择 $k$ 节点和选择 $k$ 节点的所有路径中的最短路径长度。然后就可以从 $k=0$ 开始，一直到 $k=N$ 进行递归地求解。

Floyd–Warshall 算法的一般步骤

1. 初始化数组

• 需要使用到大小为 $|V|\times |V|$ 的数组 $dist$， $dist[i][j]$ 用来存储从节点 $i$ 到节点 $j$ 的最短距离，最开始将数组中的值初始化为 $+\infty$。
• 遍历所有边，初始化 $dist[u][v]=w(u,v)$。
• 初始化所有顶点到自身的距离为 $0$， $dist[v][v]=0$

2. 递归求解结果：

• 求解使用 { 1 } , { 1 , 2 } , { 1 , 2 , 3 } , . . . { 1 , 2 , . . . , N } \{1\},\{1,2\},\{1,2,3\},...\{1,2,...,N\} {1},{1,2},{1,2,3},...{1,2,...,N} 集合中节点的最短路径

下面是 Floyd–Warshall 算法的伪代码实现，展示了它执行的一般步骤^[6]

let dist be a |V|×|V| array of minimum distances initialized to INF
let prev be a |V|×|V| array of vertex indices initialized to null

procedure FloydWarshallWithPathReconstruction() is
    for each edge (u, v) do
        dist[u][v] = w(u, v)  // The weight of the edge (u, v)
        prev[u][v] = u
    for each vertex v do
        dist[v][v] = 0
        prev[v][v] = v
    for k from 1 to |V| do // standard Floyd-Warshall implementation
        for i from 1 to |V|
            for j from 1 to |V|
                if dist[i][j] > dist[i][k] + dist[k][j] then
                    dist[i][j] = dist[i][k] + dist[k][j]
                    prev[i][j] = prev[k][j]

procedure Path(u, v) is
    if prev[u][v] = null then
        return []
    path = [v]
    while u ≠ v do
        v = prev[u][v]
        path.prepend(v)
    return path

Floyd–Warshall 算法的执行过程（一个例子）

  下面用一个例子来具体演示 Floyd–Warshall 算法的执行过程^[6]
  

  当 $k=0$ 时，不使用除了起始节点之外的任何节点（中间节点），所以全部最短路径仅有一条边得到。
  当 $k=1$ 时，最短路径的中间节点在 { 1 } \{1\} {1} 中。
  当 $k=2$ 时，最短路径的中间节点在 { 1 , 2 } \{1, 2\} {1,2} 中，可以看到，这里使用到了前面更新的路径 2->1->3。
  当 $k=3$ 时，最短路径的中间节点在 { 1 , 2 , 3 } \{1, 2, 3\} {1,2,3} 中。
  当 $k=4$ 时，最短路径的中间节点在 { 1 , 2 , 3 , 4 } \{1, 2, 3, 4\} {1,2,3,4} 中。
  于是得到了最终的结果。

Floyd–Warshall 算法的具体步骤及代码实现

输入描述：

• 给定具有 n 个顶点的图，图的边用二维数组 edges 表示，其中 edges[i] = (u,v,w) 表示一条从 u 节点到 v 节点的长度为 w 的有向边。

输出描述：

• 输出一个 n × n 的矩阵 dist，dist[i][j] 表示从 i 节点到 j 节点的最短距离。

vector<vector<int>> shortestPath(int n, vector<vector<int>>& edges){
    vector<vector<int>> dist(n, vector<int>(n, INT_MAX));
    for(auto &edge:edges){
        int u = edge[0], v = edge[1], w = edge[2];
        dist[u][v] = w;
        dist[v][u] = w;
    }
    for(int i=0;i<n;++i){
        dist[i][i] = 0;
    }
    for(int k=0;k<n;++k){
        for(int i=0;i<n;++i){
            for(int j=0;j<n;++j){
                if(dist[i][k]!=INT_MAX && dist[k][j]!=INT_MAX && dist[i][j]>dist[i][k]+dist[k][j]){
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }
    return dist;
}

Floyd–Warshall 算法的正确性证明

  由于 Floyd–Warshall 算法是使用了动态规划的算法来进行求解的，因此在计算过程中就相当于对所有可能得到的路径情况进行了判断和取舍，所以最终得到的结果一定是最优的。

例题

一般图的 Dijkstra 算法

743. 网络延迟时间

题目描述：
  有 n 个网络节点，标记为 1 到 n。

  给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

  现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

思路：
  每一个节点收到信号的时间等于从节点 k 到该节点的最短距离，所有节点都收到信号的时间就是每一个节点收到信号的时间的最大值。如果最大值为 Inf，说明不能使所有节点都收到信号，返回 -1。因此可以用 Dijkstra 算法求解。

代码：

class Solution {
public:
    vector<int> dijkstraByDenseGraph(vector<vector<int>>& edges, int n, int start){
        vector<vector<int>> graph(n, vector<int>(n, INT_MAX));
        for(auto &edge:edges){
            graph[edge[0]][edge[1]] = edge[2];
        }

        vector<int> dis(n, INT_MAX);
        dis[start] = 0;
        vector<bool> vis(n, false); 
        vector<int> par(n, -1);

        while(true){
            int u = -1, d = INT_MAX;
            //选择当前未遍历节点中距离最小的节点遍历
            for(int i=0;i<n;++i){
                if(!vis[i] && dis[i]<d){
                    d = dis[i];
                    u = i;
                }
            }

            if(u==-1) break;  //所有能遍历的节点都遍历完
            vis[u] = true;

            //更新节点 u 的所有相邻节点
            for(int v=0;v<n;++v){
                if(graph[u][v]!=INT_MAX && d+graph[u][v] < dis[v]){
                    dis[v] = d+graph[u][v];
                    par[v] = u;
                }
            }
        }

        return dis;
    }

    vector<int> dijkstraBySparseGraph(vector<vector<int>>& edges, int n, int start){
        vector<vector<pair<int,int>>> graph(n);
        for(auto& edge:edges){
            graph[edge[0]].emplace_back(edge[1], edge[2]);
        }

        vector<int> dis(n, INT_MAX); //dis[i] 记录节点 i 到节点 start 的最短距离
        dis[start] = 0;
        vector<bool> vis(n, false);  //vis[i] 记录节点 i 是否已经遍历
        vector<int> par(n, -1);      //如果题目不需要求最短路径，只求长度，则不需要记录该数组

        priority_queue<pair<int,int>, vector<pair<int,int>>, std::greater<>> pq;

        pq.emplace(0, start);        //首先加入start节点
        while(!pq.empty()){
            //选择当前未遍历节点中距离最小的节点
            auto [d, u] = pq.top();  
            pq.pop();
            if(vis[u]) continue;     
            vis[u] = true;           

            //更新该节点的所有相邻节点
            for(auto &[v, w]:graph[u]){
                if(d+w<dis[v]){
                    pq.emplace(d+w, v);
                    dis[v] = d+w;
                    par[v] = u;
                }
            }
        }

        return dis;
    }

    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        for(auto &time:times){
            time[0]--;
            time[1]--;
        }

        vector<int> dis = dijkstraByDenseGraph(times, n, k-1);
        int ans = *max_element(dis.begin(), dis.end());
        return ans==INT_MAX?-1:ans;
    }
};

网格图的 Dijkstra 算法

3341. 到达最后一个房间的最少时间 I

题目描述：
  有一个地窖，地窖中有 n x m 个房间，它们呈网格状排布。

  给你一个大小为 n x m 的二维数组 moveTime ，其中 moveTime[i][j] 表示房间开启并可达所需的 最小 秒数。你在时刻 t = 0 时从房间 (0, 0) 出发，每次可以移动到 相邻 的一个房间。在 相邻 房间之间移动需要的时间为 1 秒。

  请你返回到达房间 (n - 1, m - 1) 所需要的 最少 时间。

  如果两个房间有一条公共边（可以是水平的也可以是竖直的），那么我们称这两个房间是 相邻 的。

思路：
  题目相当于要求我们求起点到终点的单源最短路径，因此我们可以用 Dijkstra 算法求解。
  该网格图的边是四方向的，我们不用额外建图，每次遍历这四个方向上的节点就行，注意边界条件。
  遍历边 (u, v, w) 时，dis[v] = max(moveTime[i]+1, min(dis[v], dis[u]+w))，因为要保证 dis[v] 为起点到 v 的最短单源路径，而且要大于等于 moveTime[i]+1，保证此时房间已经开启。
  注意房间开启时 moveTime[i][j] 时刻才可以往该房间移动，故到达时间最小为 moveTime[i][j] + 1。

代码：

struct Node{
   int x,y,val;
   Node(int a,int b, int c):x(a),y(b),val(c){}  
};
class Solution {
public:
    int minTimeToReach(vector<vector<int>>& moveTime) {
        int n = moveTime.size();
        int m = moveTime[0].size();
        vector<vector<bool>>visited(n, vector<bool>(m));
        vector<vector<int>>time(n, vector<int>(m, INT_MAX));
        auto cmp = [](const Node& node1, const Node& node2)->bool{
            return node1.val > node2.val;
        };
        priority_queue<Node, vector<Node>, decltype(cmp)>pq(cmp);
        pq.emplace(0,0,0);
        time[0][0] = 0;
        while(!pq.empty()){
            auto [x,y,v] = pq.top();
            pq.pop();
            if(!visited[x][y]){
                visited[x][y] = true;
                vector<pair<int,int>>pa = {{x-1,y},{x+1,y},{x,y-1},{x,y+1}};
                for(auto [i,j] : pa){
                    if(i<0 || j<0 || i>=n || j>=m) continue;
                    if(!visited[i][j]){
                        time[i][j] = max(moveTime[i][j]+1,min(time[i][j], time[x][y]+1));
                        pq.emplace(i,j,time[i][j]);
                    }
                }                
            }
        }
        return time[n-1][m-1];
    }
};

3342. 到达最后一个房间的最少时间 II

题目描述：
  有一个地窖，地窖中有 n x m 个房间，它们呈网格状排布。
  给你一个大小为 n x m 的二维数组 moveTime ，其中 moveTime[i][j] 表示房间开启并可达所需的 最小 秒数。你在时刻 t = 0 时从房间 (0, 0) 出发，每次可以移动到 相邻 的一个房间。在 相邻 房间之间移动需要的时间为：第一次花费 1 秒，第二次花费 2 秒，第三次花费 1 秒，第四次花费 2 秒……如此 往复 。。
  请你返回到达房间 (n - 1, m - 1) 所需要的 最少 时间。
  如果两个房间有一条公共边（可以是水平的也可以是竖直的），那么我们称这两个房间是 相邻 的。

思路：
  和上一题类似，但是这一题需要注意到从 (i, j) 位置开始移动需要花费的时间为 (i+j)%2+1 秒。

代码：

class Solution {
public:
    int minTimeToReach(vector<vector<int>>& moveTime) {
        int m = moveTime.size(), n = moveTime[0].size();
        vector<array<int,2>> dirs = {{1,0},{-1,0},{0,1},{0,-1}};
        vector<vector<int>> dis(m, vector<int>(n, INT_MAX));
        priority_queue<tuple<int,int,int>, vector<tuple<int,int,int>>, greater<tuple<int,int,int>>> pq;//val,i,j
        pq.emplace(0,0,0);
        while(!pq.empty()){
            auto [val, i, j] = pq.top();
            pq.pop();
            if(i==m-1 && j==n-1) return val;
            if(val>dis[i][j]) continue;
            for(auto &dir:dirs){
                int x = i+dir[0], y = j+dir[1];
                if(x<0 || y<0 || x>=m || y>=n) continue;
                int newdis = max(val, moveTime[x][y])+(i+j)%2+1;
                if(dis[x][y]>newdis){
                    dis[x][y] = newdis;
                    pq.emplace(newdis, x, y);
                }
            }
        }
        return 0;
    }
};

Bellman-Ford 算法

2642. 设计可以求最短路径的图类

题目描述:
  给你一个有 n 个节点的 有向带权 图，节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示，其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。
  请你实现一个 Graph 类：

• Graph(int n, int[][] edges) 初始化图有 n 个节点，并输入初始边。
• addEdge(int[] edge) 向边集中添加一条边，其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
• int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在，返回 -1 。一条路径的代价是路径中所有边代价之和。

代码:

class Graph {
private:
    vector<vector<int>> edges;
    int n;
public:
    Graph(int n, vector<vector<int>>& edges) {
        this->n = n;
        this->edges = edges;
    }
    
    void addEdge(vector<int> edge) {
        edges.emplace_back(edge);
    }
    
    int shortestPath(int node1, int node2) {
        vector<int> distance(n, INT_MAX);
        vector<int> predecessor(n, -1);
        distance[node1] = 0;

        //进行 |V|-1 轮松弛操作
        for(int i=0;i<n-1;++i){
            bool updated = false;
            for(auto &edge:edges){
                int u = edge[0], v = edge[1], w = edge[2];
                if(distance[u]!=INT_MAX && distance[u]+w<distance[v]){
                    distance[v] = distance[u]+w;
                    predecessor[v] = u;
                    updated = true;
                }
            }
            if(!updated) break;
        }

        //检测是否有负权环
        for(auto &edge:edges){
            int u = edge[0], v = edge[1], w = edge[2];
            if(distance[u]!=INT_MAX && distance[u]+w<distance[v]){
                //存在负权环，算法不收敛
                vector<bool> vis(n, false);
                while(!vis[u]){
                    vis[u] = true;
                    u = predecessor[u];
                }
                cout<<"存在负权环，节点 "<<u<<" 是该负权环上的点"<<endl;
                return -1;
            }
        }

        return distance[node2]==INT_MAX?-1:distance[node2];
    }
};

U520022 Bellman_ford

题目描述:
  给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数。
  请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。
  注意：图中可能存在负权回路。

输入格式:
  第一行包含三个整数 n,m,k。
  接下来 m 行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。
  点的编号为 1∼n。

输出格式:
  输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
  如果不存在满足条件的路径，则输出 impossible。

代码:

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main(){
    int n,m,k;
    cin>>n>>m>>k;
    vector<tuple<int,int,int>> edges;
    for(int i=0;i<m;++i){
        int x,y,z;
        cin>>x>>y>>z;
        edges.emplace_back(x,y,z);
    }
    vector<int> dis(n+1, INT_MAX);
    dis[1] = 0;
    for(int i=0;i<k;++i){
        vector<int> temp_dis = dis;
        bool updated = false;
        for(auto [u,v,w]:edges){
            if(dis[u]!=INT_MAX && dis[u]+w<temp_dis[v]){
                temp_dis[v] = dis[u]+w;
                updated = true;
            }
        }
        dis = temp_dis;
        if(!updated) break;
    }
    if(dis[n]==INT_MAX){
        cout<<"impossible";
    }
    else{
        cout<<dis[n];
    }
}

P3385 【模板】负环

题目描述
  给定一个 n 个点的有向图，请求出图中是否存在从顶点 1 出发能到达的负环。
  负环的定义是：一条边权之和为负数的回路。

输入格式
  本题单测试点有多组测试数据。
  输入的第一行是一个整数 T，表示测试数据的组数。对于每组数据的格式如下：
  第一行有两个整数，分别表示图的点数 n 和接下来给出边信息的条数 m。
  接下来 m 行，每行三个整数 u,v,w。
  若 w≥0，则表示存在一条从 u 至 v 边权为 w 的边，还存在一条从 v 至 u 边权为 w 的边。
  若 w<0，则只表示存在一条从 u 至 v 边权为 w 的边。

输出格式
  对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
    int T;
    cin>>T;
    for(int i=0;i<T;++i){
        int n,m;
        cin>>n>>m;
        vector<int> dist(n+1, INT_MAX);
        vector<tuple<int,int,int>> edges;
        for(int j=0;j<m;++j){
            int u,v,w;
            cin>>u>>v>>w;
            edges.emplace_back(u,v,w);
            if(w>=0){
                edges.emplace_back(v,u,w);
            }
        }
        dist[1] = 0;
        for(int k=0;k<n-1;++k){
            bool updated = false;
            for(auto [u,v,w]:edges){
                if(dist[u]!=INT_MAX && dist[u]+w<dist[v]){
                    dist[v] = dist[u]+w;
                    updated = true;
                } 
            }   
            if(!updated) break;
        }

        bool check = false;
        for(auto [u,v,w]:edges){
            if(dist[u]!=INT_MAX && dist[u]+w<dist[v]){
                check = true;
                break;
            }
        }
        if(check){
            cout<<"YES"<<endl;
        }
        else{
            cout<<"NO"<<endl;
        }
    }
}

Floyd–Warshall 算法

1334. 阈值距离内邻居最少的城市

题目描述：
  有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。
  返回在路径距离限制为 distanceThreshold 以内可到达城市最少的城市。如果有多个这样的城市，则返回编号最大的城市。
  注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

代码：

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<int> ans(n, 0);
        vector<vector<int>> dist = shortestPath(n, edges);
        for(int i=0;i<n;++i){
            for(int j=0;j<n;++j){
                if(dist[i][j]<=distanceThreshold){
                    ans[i]++;
                }
            }
        }
        int rs = -1, ts = INT_MAX;
        for(int i=0;i<n;++i){
            if(ts>=ans[i]){
                rs = i;
                ts = ans[i];
            }
        }
        return rs;
    }

    vector<vector<int>> shortestPath(int n, vector<vector<int>>& edges){
        vector<vector<int>> dist(n, vector<int>(n, INT_MAX));
        for(auto &edge:edges){
            int u = edge[0], v = edge[1], w = edge[2];
            dist[u][v] = w;
            dist[v][u] = w;
        }
        for(int i=0;i<n;++i){
            dist[i][i] = 0;
        }
        for(int k=0;k<n;++k){
            for(int i=0;i<n;++i){
                for(int j=0;j<n;++j){
                    if(dist[i][k]!=INT_MAX && dist[k][j]!=INT_MAX && dist[i][j]>dist[i][k]+dist[k][j]){
                        dist[i][j] = dist[i][k] + dist[k][j];
                    }
                }
            }
        }
        return dist;
    }
};

参考文献

[1]. 从0开始数.【算法】最短路径查找—Dijkstra算法 视频讲解
[2]. 灵茶山艾府. 两种 Dijkstra 写法（附题单）Python/Java/C++/Go/JS/Rust
[3]. WIKIPEDIA. Bellman–Ford algorithm
[4]. 波波微课. Bellman-Ford最短路径算法 视频讲解
[5]. 灵茶山艾府. 带你发明 Floyd 算法：从记忆化搜索到递推（Python/Java/C++/Go/JS/Rust）
[6]. WIKIPEDIA. Floyd–Warshall algorithm